ความดันและแรงดัน

      แรงดัน (Force) คือ แรงหรือน้ำหนักทั้งหมดที่กดลงบนพื้นที่ทั้งหมด

      ความดัน (Pressure) คือ แรงดันบนพื้นที่ 1 ตารางหน่วย

      ความดันของของไหล คือ อัตราส่วนของแรงที่กระทำต่อวัตถุต่อหน่วยพื้นที่ที่สัมผัสกับของไหล

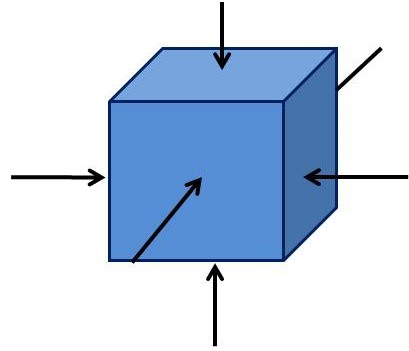
ภาพที่ 1 แรงดันของบรรยากาศที่กระทำต่อวัตถุทุกทิศทุกทาง

ที่มา: กัญญา  เกื้อกูล

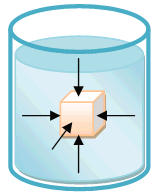
ภาพที่ 2 แสดงแรงดันของของเหลว
ที่มา : https://sites.google.com/site/physickwamronkhonglai/khwam-rxn/khxnghil

สมมติ บนพื้นที่ A ตร.ม. มีแรงดัน F นิวตัน

         ดังนั้น บนพื้นที่ 1 ตร.ม. มีแรงดัน F/A  นิวตัน

         แต่แรงดันบน 1 หน่วยพื้นที่เรียกว่า ความดัน

สูตรความสัมพันธ์ 

                       P=F/A   

          เมื่อ   P  คือ ความดัน มีหน่วยเป็น N/m² หรือพาสคัล (pascal:Pa) 
                   F  คือ แรงที่ของเหลวกระทำต่อวัตถุ (นิวตัน) 
                   A  คือ พื้นที่ (ตารางเมตร) และเป็นพื้นที่ราบ (Flat area)

         ระบบ SI ปาสคาล (Pascal)  =  นิวตันต่อตารางเมตร
          ทางอุตุนิยมวิทยา  1 บาร์ (Bar)  =  10⁵ ปาสคาล
                              1 บรรยากาศ (Atmosphere)  =  1.01 บาร์
                                                                         =  1.01 x 10⁵ ปาสคาล

ความดันในของเหลวจะแปรผันตรงกับความลึกและความหนาแน่นของของเหลว

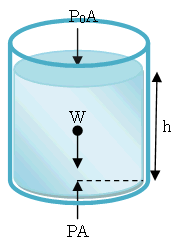
ภาพที่ 3 แสดงความดันของของเหลว
ที่มา : https://sites.google.com/site/physickwamronkhonglai/khwam-rxn/khxnghil

หากเราพิจารณาของเหลวที่มีความหนาแน่นอยู่นิ่งในภาชนะเปิดสู่บรรยากาศ

          W เป็นน้ำหนักของของเหลวบนพื้นที่ A (หน้าตัดของทรงกระบอก) ดังนั้น  

         ให้ความดันบรรยากาศ คือ P_o  เนื่องจากของเหลวอยู่ในสมดุล ดังนั้นที่ก้นแก้ว

         จะได้  สูตรความดันสัมบูรณ์      

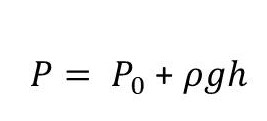
          เมื่อ          P     คือ ผลรวมของความดันบรรยากาศกับความดันเกจ  เรียกว่า "ความดันสัมบูรณ์"  (Absolute pressure)

                         P₀       คือ ความดันที่ผิวของเหลวเท่ากับความดันบรรยากาศ 

                             เป็นความดันเนื่องจากน้ำหนักของของเหลวที่ระดับความลึก h เรียกว่า " ความดันเกจ "

จากสูตร สรุปได้ว่า ความดันในของเหลวชนิดเดียวกันที่ระดับความลึกเดียวกันมีค่าเท่ากันโดยรูปทรงของภาชนะไม่มีผลต่อความดัน

การจำแนกชนิดของความดัน

          1. ความดันบรรยากาศ ( Atmospheric Pressure : Po ) คือ ความดันที่เกิดจากบรรยากาศที่ทับถมอยู่เหนือจุดที่พิจารณา มีค่าเท่ากับน้ำหนักของอากาศในชั้นบรรยากาศที่ทับถมอยู่เหนือพื้นที่ 1 ตารางหน่วยซึ่ง ความดันบรรยากาศปกติ ที่ระดับน้ำทะเล คือ 1 บรรยากาศ ( 1 atm)

              P_o = 1.01235 X 10⁵ N/m²

          2. ความดันเกจ ( Gauge Pressure : Pg ) คือ ความดันเนื่องจากน้ำหนักของของเหลวเพียงอย่างเดียว

          3. ความดันสัมบูรณ์ (Absolute Pressure : P) คือ ผลรวมของความดันบรรยากาศกับความดันเกจรวม

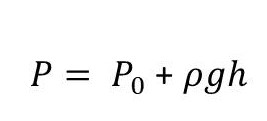
ลักษณะของความดันของของเหลว

          1. ทุกๆ จุดในของเหลวจะมีแรงดันจากทุกทิศทาง

          2. ความดันของของเหลวขึ้นอยู่กับความลึกเเละความหนาเเน่นของของเหลว โดยไม่ขึ้นกับปริมาตรของของเหลว

          3. ภาชนะที่มีของเหลวบรรจุอยู่จะได้รับแรงดันจากของเหลวกระทำต่อผนังภาชนะใน แนวตั้งฉากกับผนังภาชนะ เช่น สังเกตน้ำที่พุ่งออกมาจากรอยรั่วของถังน้ำ แสดงถึงว่าจะต้องมีแรงดันของน้ำกระทำต่อพื้นที่ด้านข้างถัง และแรงดันนี้จะดันให้น้ำพุ่งออกมาตามรอยรั่วได้

          4. ภายใต้สภาพแรงดึงดูดของโลก ความดันของของเหลว ณ ตำแหน่งใด ๆ ขึ้นกับความลึกของตำแหน่งนั้น วัดจากผิวของของเหลวและความหนาแน่นของของเหลว ตามสมการ

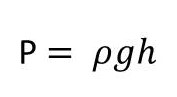
แรงดันที่กระทำต่อก้นภาชนะ
          ภาชนะที่บรรจุของเหลว จะมีแรงดันเนื่องจากของเหลวกระทำในทิศตั้งฉากกับพื้นที่ผิวภาชนะที่ของเหลวสัมผัส โดยขนาดของแรงดันหาได้จากผลคูณของความดันของของเหลวกับพื้นที่ที่ของเหลวสัมผัส            ( F = PA ) แต่เนื่องจากความดันของของเหลวขึ้นอยู่กับความลึก ดังนั้นความดันที่กระทำกับก้นภาชนะจะเป็นความดันสัมบูรณ์

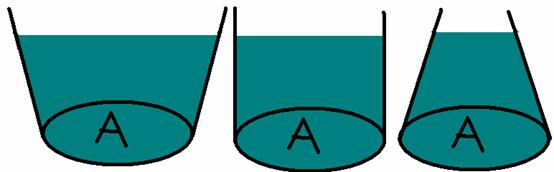
ภาพที่ 4 แสดงภาชนะบรรจุน้ำ 3 ขนาดที่มีความสูงเท่ากัน
ที่มา : http://drvandgrengchemicalliquid.tripod.com/pressure2.htm

          จากรูปความดันที่ของเหลวกดก้นภาชนะทั้ง 3 รูปมีค่าเท่ากัน 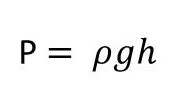   (h เท่ากัน) และแรงดันที่ของเหลวกดก้นภาชนะทั้ง 3 รูปมีค่าเท่ากัน F = PA =         (A เท่ากัน)

แรงดันที่กระทำต่อผนังภาชนะ
          เนื่องจากความดันของของเหลวขึ้นอยู่กับความลึก ดังนั้นความดันที่กระทำกับผนังภาชนะจะเป็นความดันเฉลี่ยระหว่างจุดสูงสุดและจุดต่ำสุดของของเหลว

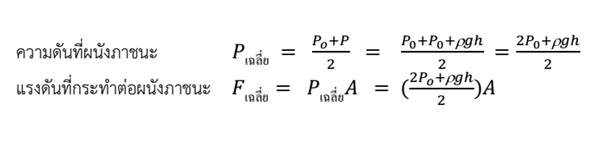
          ในกรณีการหาแรงดันน้ำที่กระทำต่อผนังภาชนะ จะหมายถึงแรงดันเนื่องจากความดันเกจ ไม่คิดผลของแรงดันบรรยากาศ แต่ถ้าหาแรงดันที่กระทำต่อผนังภาชนะ จะหมายถึงแรงดันเนื่องจากความดันสัมบูรณ์ ต้องคิดรวมความดันบรรยากาศด้วย

เครื่องมือวัดความดันของของเหลว
          1. มานอมิเตอร์ ( Manometer ) เป็นเครื่องมือวัดความดันของของไหล ประกอบด้วยหลอดแก้วรูปตัวยู ( U tube ) มีของเหลวบรรจุอยู่ภายใน ปลายข้างหนึ่งปิด ส่วนปลายอีกข้างหนึ่งจะต่อกับภาชนะบรรจุของไหลที่ต้องการวัดความดันและการรู้ความแตกต่างของระดับของเหลวในหลดแก้วรูปตัวยูทั้งสองข้างจะทำให้สามารถหาความดันของของไหลได้

หลักการคำนวณ
              ให้เปรียบเทียบระดับความสูงของของเหลวในหลอดทั้งสองข้าง
“ที่ระดับความสูงเดียวกันความดันจะมีค่าเท่ากัน”

                    P_A = P_B

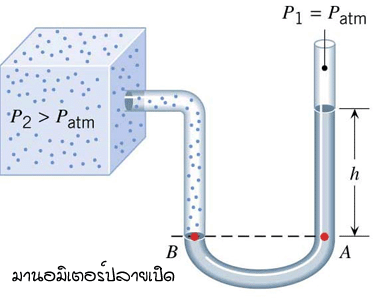
ภาพที่ 6 มานอมิเตอร์ ( Manometer )
ที่มา : http://www.rmutphysics.com/teaching-glossary/index.php?option=com_content&task=view&id=9968&Itemid=11

          2. บารอมิเตอร์ปรอท ( Mercury Barometer ) สร้างตามหลักของ เทอร์รีเชลลี (Toricelli) โดยนำหลอดแก้วปลายเปิดข้างหนึ่ง ปลายปิดข้างหนึ่ง ทำให้เป็นสุญญากาศแล้วคว่ำด้านปลายเปิดของหลอดแก้วลงไปในอ่างปรอท เมื่อหลอดแก้วอยู่ในแนวดิ่งอากาศภายนอกจะดันปรอทให้เข้าสู่หลอดแก้ว พบว่าเมื่อความดันปกติ ความสูง h ของปรอทเท่ากับ 760มิลลิเมตร แสดงว่า P_o = 760 mmHg = 76 cmHg = 1 atm

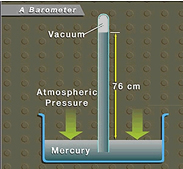
ภาพที่ 7  บารอมิเตอร์ปรอท
ที่มา : http://www.rmutphysics.com/teaching-glossary/index.php?option=com_content&task=view&id=9968&Itemid=11

แหล่งที่มา

ช่วง  ทมทิตชงค์ และคณะ. (2537). ฟิสิกส์ 3  ม.5. กรุงเทพฯ:ไฮเอ็ดพับลิชชิ่ง.

 กฎของปาสคาลและเครื่องอัดไฮโดรลิก

          กฎของปาสคาลใช้อธิบายเกี่ยวกับการส่งต่อความดันในของไหล มีหลักการว่า “ถ้าเพิ่มความดันให้กับของไหล ที่บรรจุในภาชนะปิด ณ จุดใด ความดัน นั้นจะส่งกระจายกันต่อไปทำให้ทุก ๆ ส่วนของของไหลได้รับความดันที่เพิ่มขึ้น (Increased Pressure)  เท่ากันหมด”

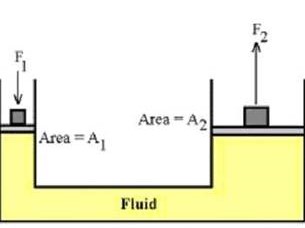
รูปที่ 1 เครื่องอัดไฮโดรลิก
ที่มา: https://indyteacher.wordpress.com/หน่วยการเรียนรู้/unit2/กฎของพาสคาล/

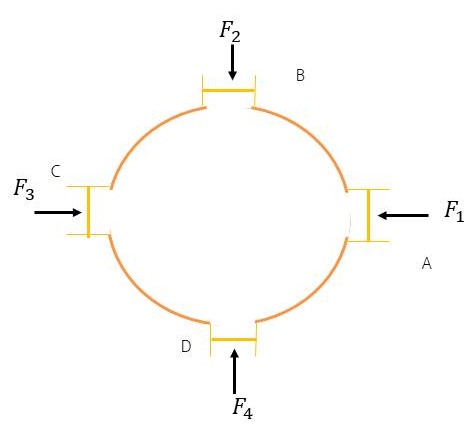
รูปที่ 2 ภาชนะใบหนึ่งใส่ของเหลวเต็มแล้วออกแรงกระทำ
ที่มา: กัญญา  เกื้อกูล

จากรูปเป็นภาชนะใบหนึ่งใส่ของเหลว เช่นน้ำไว้เต็ม , มีแรงดัน F₁ , F₂ , F₃ และ F₄  ที่ลูกสูบ A, B, C, D ตามลำดับ

          เมื่อเราออกแรงดันเพิ่มขึ้น F₁ ให้กับลูกสูบที่มีพื้นที่หน้าตัด A จะเกิดความที่เพิ่มขึ้นเป็น F₁/A มีผลทำให้เกิด ความดันเพิ่มขึ้นที่ลูกสูบ B,C  และ D เป็น F₂/B, F₃/C  และ F₄/D ซึ่งจะมีค่าเท่ากันหมดถ้าภาชนะนี้ตั้งในแนวดิ่ง ลูกสูบต่าง ๆ อาจไม่อยู่ในระดับเดียวกัน ดังนั้น

          - ของเหลวที่ดันลูกสูบในระดับเดียวกัน ย่อมมีความดันเท่ากัน

          - ความดันที่เพิ่มขึ้น แก่ลูกสูบทุกตัวเท่ากัน ตามกฎ Pascal  แม้ว่าจะไม่เป็นระดับเดียวกัน

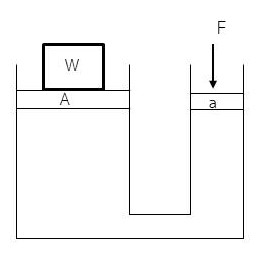
รูปที่ 3 หลอดรูปตัวยูขาโตไม่เท่ากันภายในบรรจุของไหล
ที่มา: กัญญา  เกื้อกูล

จากรูปที่ 3  เป็นหลอดรูปตัวยูขาโตไม่เท่ากัน ภายในบรรจุของไหลที่ขาทั้งสองมีลูกสูบปิดสนิท ขาข้างเล็กมีพื้นที่หน้าตัด a  ส่วนขาข้างใหญ่มีพื้นที่หน้าตัด A  เมื่อออกแรงกด F ที่ลูกสูบเล็ก (ลูกสูบกด, ลูกสูบอัด) ทำให้ลูกสูบใหญ่ (ลูกสูบยก, ลูกสูบขยาย) สามารถยกน้ำหนัก W ได้  ซึ่งเป็นหลักการทำงานของเครื่องกลผ่อนแรงที่รู้จักกันทั่วไป คือ เครื่องอัดไฮดรอลิก (hydraulic press) จากกฎของพาสคาล

          ความดันที่ใส่เพิ่มเข้าไป = ความดันที่ได้รับ

                                   P ที่ a = P ที่ A

                                       F/a = W/A

                             หรือ W/F  = A/a                                                                          …..(1)

          จากสมการที่ (1)  เมื่อ A > a ดังนั้น W > F  แสดงว่าออกแรงกดน้อยได้แรงยกมาก ซึ่งเป็นหลักการเครื่องกลผ่อนแรง

         จาก (1)  W/F   เรียกว่า  การได้เปรียบเชิงกลทางปฏิบัติ

         A/a เรียกว่า การได้เปรียบเชิงกลทางทฤษฎี (theoretical mechanical advantage)

         จาก (1)  W/F = A/a     เมื่อไม่มีแรงเสียดทานภายนอกมากระทำ

        ถ้ามีแรงเสียดทานภายนอกมากระทำ ค่าของ W จะได้น้อยกว่าที่ควรจะได้ดังนั้น W/F < A/a

ประสิทธิภาพของเครื่องกล (Eff)

          Eff = (งานที่ได้ /งานที่ให้) x100

   หรือ Eff = (M.A. ทางปฏิบัติ /M.A. ทางทฤษฎี) x 100

   หรือ Eff =  (แรงที่ได้จริง/ แรงที่ควรได้) x 100

ตัวอย่างที่ 1 ของเหลวชนิดหนึ่งอยู่ในภาชนะที่มิดชิด เมื่อเพิ่มความดันแก่ของเหลว จะได้ผลตามข้อใด

          1. ทุกจุดในของเหลวมีความดันเพิ่มขึ้นเท่ากัน

          2. ปริมาตรของเหลวเท่าเดิม

          3. แรงกระทำต่อภาชนะเพิ่มขึ้น

          4. ถูกทุกข้อ

เฉลยข้อที่ถูกต้อง คือข้อ 4 เพราะจากกฎของ Pascal เมื่อให้ความดันเพิ่มขึ้น,แก่ผิวของของไหล ความดันจะกระจายออกไป จนทำให้ผิวของเหลวมีความดันที่เพิ่มขึ้นเท่ากันหมด

ตัวอย่างที่ 2 จากกฎของปาสคาลนำมาสร้างเครื่องอัดไฮดรอลิก จงพิจารณาข้อความต่อไปนี้

           A. เมื่อออกแรงกดลูกสูบข้างหนึ่ง, ลูกสูบอีกข้างหนึ่งจะเคลื่อนที่ขึ้นแสดงว่าเราสามารถส่งแรงดันผ่านของเหลวได้

           B. ขณะลูกสูบสมดุลวัตถุพอดียกขึ้น ความดันของของเหลวที่กระทำต่อลูกสูบทั้งสองมีค่าเท่ากัน

          C. แรงที่กดลงบนลูกสูบอัด และลูกสูบยกเท่ากัน

เราอาจสรุปหลักการได้ตามข้อใด

          1. ข้อ A, B, C ถูกต้อง 2. ข้อ A, B ถูกต้อง  

          3. ข้อ B, C ถูกต้อง     4. ข้อ A,  C ถูกต้อง  

เฉลยข้อ 4 ถูกต้อง เพราะจากกฎของปาสคาล ถ้าเพิ่มความดันให้กับของไหล ที่บรรจุในภาชนะปิด ณ จุดใด ความดัน นั้นจะส่งกระจายกันต่อไปทำให้ทุก ๆ ส่วนของของไหลได้รับความดันที่เพิ่มขึ้น (Increased Pressure)  เท่ากันหมด

ตัวอย่างที่ 3 เครื่องอัดไฮดรอลิกที่มีคานโยกจะผ่อนแรงมากเมื่อใด

          1. ระยะก้านสูบอัดถึงจุดหมุนยาวกว่าระยะจุดหมุนถึงปลายคานโยก

          2. ระยะก้านสูบอัดถึงจุดหมุนเท่ากับระยะจุดหมุนถึงปลายคานโยก

          3. ระยะก้านสูบอัดถึงจุดหมุนสั้นกว่า ระยะจุดหมุนถึงปลายคานโยกมาก ๆ

          4. ใช้ก้านสูบอัดเป็นจุดหมุนออกแรงกดปลายคาน

เฉลยข้อที่ถูกต้องคือ ข้อ 3 เพราะ แขนของแรงพยายามยาวจะผ่อนแรงมาก 

ตัวอย่างที่ 4 เครื่องอัดบรามาห์เครื่องหนึ่งมีพื้นที่หน้าตัดของลูกสูบใหญ่เป็น 5  เท่าของลูกสูบเล็ก ในการใช้ยกของหนัก 1000  นิวตัน ต้องออกแรงที่ลูกสูบเล็กกี่นิวตัน

เฉลย จาก F/a = W/A

              F/W = a/A

         F/1000 = 1/5

                  F = 200  นิวตัน

ตอบ แรงที่ลูกสูบเล็ก = 200  นิวตัน

ตัวอย่างที่ 5 จงพิจารณาข้อความต่อไปนี้ข้อใดถูกต้องเกี่ยวกับกฎของปาสคาล

           1. ความดันที่กระทำที่จุดใด ๆ ในของเหลว ณ ระดับความลึกเดียวกันจะมีค่าเท่ากันหมด

           2. ความดันของของเหลวที่กระทำเมื่ออยู่ในภาชนะที่ปิด จะมีทิศทางตั้งฉากกับผนังด้านในของวัตถุเสมอ

          3. ความดันที่กระทำต่อส่วนใดส่วนหนึ่งของของเหลวในภาชนะปิด จะส่งผ่านไปยังทุกทิศทุกทางโดยมีการเปลี่ยนแปลงตามความหนาแน่นของของเหลว

         4. เมื่อมีความดันที่เพิ่มขึ้นกระทำต่อส่วนหนึ่งส่วนใดของของเหลวหรือของไหลในภาชนะปิด, ความดันที่เพิ่มขึ้นจะส่งผ่านไปยังทุก ๆ ส่วนของของเหลวหรือของไหลรวมทั้งผนังของภาชนะที่บรรจุโดยไม่มีการเปลี่ยนแปลง

เฉลยข้อที่ถูกต้องคือ ข้อ 4               

ตัวอย่างที่ 6 พื้นที่หน้าตัดขวางของลูกสูบเล็กในเครื่องอัดบรามาห์ เท่ากับ 6 ตารางเซนติเมตร และลูกสูบใหญ่เท่ากับ 600 ตารางเซนติเมตร การได้เปรียบเชิงกลของคานคือที่สำหรับโยกขึ้นลงเท่ากับ 4 ถ้าออกแรงโยกที่คานถือ 500  นิวตัน ลูกสูบใหญ่จะยกน้ำหนักเท่าใด

เฉลย สิ่งที่โจทย์กำหนดให้ คานโยกผ่อน 4 เท่า

             F_{รูปเล็ก}  = 4 x 500 = 2000 นิวตัน

  จากสมการ F/a = W/a

             2000/6 = W/600

                    W = 2x 10⁵ นิวตัน

ตอบ ลูกสูบใหญ่จะยกน้ำหนัก = 2x 10⁵ นิวตัน

แหล่งที่มา

นิรันดร์  สุวรัตน์. (2551). ฟิสิกส์ ม.5 เล่ม 1-2. กรุงเทพฯ:พัฒนาศึกษา.

ช่วง  ทมทิตชงค์ และคณะ. (2537). ฟิสิกส์ 3  ม.5. กรุงเทพฯ:ไฮเอ็ดพับลิชชิ่ง.

Fluid Mechanics for Students. (มมป.)  กฎของปาสคาล. สืบค้นเมื่อ 10 ตุลาคม 2562,  https://indyteacher.wordpress.com/หน่วยการเรียนรู้/unit2/กฎของพาสคาล/

รูปที่ 1 การวัดปริมาตรของวัตถุจากปริมาตรของเหลวที่ล้นออกมา
ที่มา : https://www.blockdit.com/articles/5d90d88ed9718d0cbf9214cb

          หลักการของอาร์คิมิดีส (Archimedes' principle) ตั้งชื่อตามอาร์คิมิดีสแห่งซีราคิวส์ ผู้ค้นพบกฎนี้เป็นคนแรก ซึ่งเป็นกฎเกี่ยวกับแรงลอยตัวและการแทนที่ โดยกล่าวว่า เมื่อนำวัตถุลงไปแทนที่ของเหลวจะมีแรงต้านเท่ากับน้ำหนักของของเหลวปริมาตรเท่าส่วนจม จากหลักการนี้ทำให้เข้าใจในหลักการหลายอย่าง เช่น เรือเหล็กทำไมจึงลอยน้ำ ของเหลวต่างชนิดกันมีความหนาแน่นต่างกัน อาร์คีมีดีสชี้ให้เห็นถึงเรื่องความหนาแน่นและนำมาเทียบกับน้ำเรียกว่าความถ่วงจำเพาะ จากหลักการนี้ทำให้อาร์ดีมีดีสสามารถพิสูจน์มงกุฎทองคำ ที่ช่างทำมงกุฎหลอมสิ่งเจือปนลงไปในเนื้อทอง อาร์คีมีดีสหาวิธีวัดปริมาตรมงกุฎทองคำได้ด้วยการเอาไปแทนที่น้ำ และปล่อยให้น้ำล้นออกมา สาระสำคัญของหลักการของอาร์คีมีดิส

1. ปริมาตรของเหลวที่ถูกแทนที่ จะเท่ากับปริมาตรของวัตถุส่วนที่จมลงในของเหลว
2. น้ำหนักของวัตถุที่่ชั่งในของเหลว จะมีค่าน้อยกว่าน้ำหนักของวัตถุที่ชั่งในอากาศ เนื่องจากแรงพยุงของของเหลวมีมากกว่าแรงพยุงของอากาศ
3. น้ำหนักของวัตถุที่หายไปในของเหลว จะเท่ากับน้ำหนักของของเหลวที่ถูกวัตถุแทนที่ ซึ่งคำนวณได้จากผลต่างของน้ำหนักของวัตถุที่ชั่งในอากาศกับน้ำหนักของวัตถุที่ชั่งในของเหลว
4. น้ำหนักของของเหลวที่ถูกแทนที่ จะเท่ากับน้ำหนักของของเหลวที่มีปริมาตรเท่ากับวัตถุส่วนที่จม

แรงลอยตัว (Buoyancy)

            แรงลอยตัว คือ แรงพยุงของของเหลวและแก๊สที่กระทำต่อวัตถุที่อยู่ในของเหลวและแก๊สนั้น ทำให้วัตถุลอยอยู่ได้ โดยในชีวิตประจำวันเราจะพบว่าวัตถุบางชนิดลอยอยู่ในน้ำได้ เพราะแรงลอยตัวที่กระทำต่อวัตถุนั้นมีค่าเพียงพอที่จะต้านน้ำหนักของวัตถุ ที่เกิดจากแรงโน้มถ่วงของโลกได้ แต่สำหรับวัตถุบางชนิดที่จมลงในน้ำ แสดงว่าแรงลอยตัวที่กระทำต่อวัตถุนั้นมีค่าน้อยกว่าน้ำหนักของวัตถุ

สมการที่ใช้ในการคำนวณหาขนาดของแรงลอยตัวเป็นดังนี้

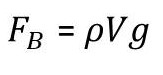
เมื่อ      คือ ความหนาแน่นของของเหลว มีหน่วยเป็น กิโลกรัม/ลูกบาศก์เมตร (kg/m3 )

               V          คือ ปริมาตรของของเหลวที่ถูกแทนที่ มีหน่วยเป็น ลูกบาศก์เมตร (m ³ )

               G          คือ ขนาดความเร่งเนื่องจากแรงโน้มถ่วงของโลก มีหน่วยเป็น เมตร/วินาที² (m/s² )

                F_B       คือ ขนาดของแรงพยุง มีหน่วยเป็น นิวตัน (N)

ตัวอย่างที่ 1 วัตถุหนึ่งเมื่อแขวนบนเครื่องชั่งสปริงในอากาศอ่านค่าน้ำหนักได้ 28.6 นิวตัน แต่เมื่อนำวัตถุ นี้ที่แขวนบนเครื่องชั่งสปริงไปจุ่มลงในน้ำจนจมทั้งก้อนอ่านค่าน้ำหนักได้ 25.8 นิวตัน วัตถุนี้มีปริมาตรเท่าใด (กำหนดให้ ความหนาแน่นของน้ำ = 1x10³ kg/m³ และ ค่าความเร่งโน้มถ่วงของโลก(g) = 10 m/s² )

วิธีทำ โจทย์กำหนดให้ น้ำหนักของวัตถุเมื่อชั่งในอากาศ = 28.6 N

          น้ำหนักของวัตถุเมื่อชั่งในน้ำ = 26.7 N

                       จาก แรงพยุง (F_B ) = น้ำหนักของวัตถุที่ชั่งในอากาศ – น้ำหนักของวัตถุเมื่อชั่งในน้ำ

                  แทนค่า แรงพยุง (F_B ) = 28.6 – 25.8 = 2.8 N

                       จาก

                       แทนค่า

                                             2.8 = (1x10³) V(10)

                                               V = 2.8 x 10^-4 m³

ตอบ วัตถุนี้มีปริมาตรเท่ากับ 2.8 x 10^-4 ลูกบาศก์เมตร

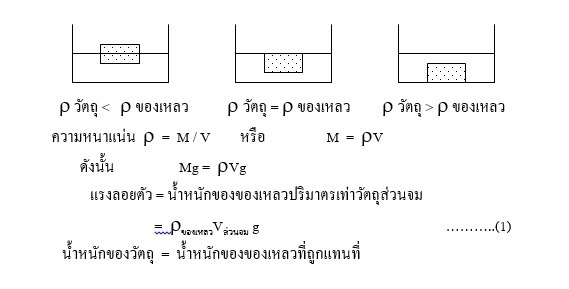
ดังนั้น แรงพยุงหรือแรงลอยตัวที่ของเหลวกระทำต่อวัตถุมีขนาดเท่ากับน้ำหนักของของเหลวที่มีปริมาตร เท่ากับปริมาตรของวัตถุส่วนที่จมอยู่ในของเหลว จึงสามารถสรุปได้ว่า

          1. วัตถุที่มีความหนาแน่นมากกว่าความหนาแน่นของเหลว วัตถุจะจมในของเหลวนั้น

          2. วัตถุที่มีความหนาแน่นเท่ากับความหนาแน่นของเหลว วัตถุจะลอยในของเหลวปริ่มเสมอกับ ผิวของเหลวนั้น

          3. วัตถุที่มีความหนาแน่นน้อยกว่าความหนาแน่นของเหลว วัตถุจะลอยในของเหลวโดยมี บางส่วนจมอยู่ในของเหลวและมีบางส่วนลอยอยู่เหนือของเหลวนั้น

รูปที่ 2 แสดงการลอยของวัตถุในของเหลวแต่ละชนิด

          ความหนาแน่นของวัตถุ (Density) คือ อัตราส่วนระหว่างมวลของวัตถุต่อปริมาตรของวัตถุ เขียนแทน ด้วยสัญลักษณ์ “      ” เรียกว่า Rho โดยความหนาแน่นจะมีหน่วยเป็น กรัมต่อลูกบาศก์เซนติเมตร (g/cm³ ) หรือ กิโลกรัมต่อลูกบาศก์เมตร (kg/m³ ) สำหรับหน่วยในระบบ S.I. เราจึงสามารถเขียนเป็นสมการได้ดังนี้

                           ความหนาแน่นของวัตถุ =  มวลของวัตถุ/ปริมาตรของวัตถุ

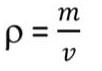
              เมื่อ    = ความหนาแน่นของวัตถุ มีหน่วยเป็น g/cm³ หรือ kg/m³

                              m       = มวลของวัตถุ มีหน่วยเป็น g หรือ kg

                              V       = ปริมาตรของวัตถุ มีหน่วยเป็น cm ³ หรือ m ³

          ความถ่วงจำเพาะ (Specific gravity) หรือความหนาแน่นสัมพัทธ์ (Relative Density) ของสารใด ๆ หมายถึง อัตราส่วนระหว่างความหนาแน่นของสารนั้นกับความหนาแน่นของสารอ้างอิง ซึ่งโดยทั่วไปนิยมใช้ความหนาแน่นของสารอ้างอิงเป็นน้ำบริสุทธิ์ที่อุณหภูมิ 4 องศาเซลเซียส ที่มีค่าความหนาแน่นเท่ากับ  1x10³  กิโลกรัม/ลูกบาศก์เมตร เช่น การหาความถ่วงจำเพาะหรือความหนาแน่นสัมพัทธ์ของตะกั่ว

ตัวอย่างที่ 1 บอลลูนสำหรับนำนักท่องเที่ยวขึ้นชมทิวทัศน์โดยรอบวนอุทยานแห่งหนึ่ง ซึ่งภายในบอลลูน บรรจุแก๊สฮีเลียมที่มีปริมาตร 600 ลูกบาศก์เมตร และมีมวล 108 กิโลกรัม ค่าความหนาแน่นของแก๊สฮีเลียมที่ บรรจุอยู่ในบอลลูนมีค่าเท่าใด

วิธีทำ

โจทย์กำหนด ปริมาตรของแก๊สฮีเลียม (V) = 600 m² ; มวลของแก๊สฮีเลียม (m) = 108 kg

จากสมการแทนค่า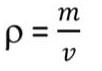                   

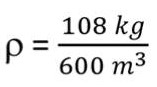
ตอบ ความหนาแน่นของแก๊สฮีเลียมมีค่าเท่ากับ 0.18 กิโลกรัม/ลูกบาศก์เมตร

          เมื่อพิจารณาการจมและการลอยของวัตถุใด ๆ ที่อยู่ในของเหลว ขึ้นอยู่กับค่าความหนาแน่นของวัตถุกับ ค่าความหนาแน่นของของเหลวนั้น ถ้าวัตถุใดจมน้ำ แสดงว่า วัตถุนั้นมีความหนาแน่นมากกว่าความหนาแน่นของน้ำ แต่ถ้าวัตถุนั้นลอยน้ำได้ แสดงว่า วัตถุนั้นมีความหนาแน่นน้อยกว่าความหนาแน่นของน้ำ หากต้องการให้วัตถุที่ มีค่าความหนาแน่นมากกว่าค่าความหนาแน่นของน้ำสามารถลอยอยู่บนผิวน้ำได้ เราต้องเปลี่ยนแปลงรูปร่างของ วัตถุเพื่อให้วัตถุมีปริมาตรเพิ่มมากขึ้น จนมีค่าความหนาแน่นน้อยกว่าค่าความหนาแน่นของน้ำ เช่น เหล็กที่มีความ หนาแน่น 7.8 กรัมต่อลูกบาศก์เซนติเมตร ซึ่งมากกว่าความหนาแน่นของน้ำเหล็กจึงจมน้ำ แต่เมื่อนำเหล็กมาทำ เป็นเรือเหล็กจะสามารถลอยน้ำได้ ที่เป็นเช่นนี้เนื่องจากเราทำให้เรือเหล็กมีปริมาตรเพิ่มขึ้นขณะที่มวลของเหล็ก ยังคงเท่าเดิม จึงส่งผลให้ความหนาแน่นของเรือเหล็กน้อยกว่าความหนาแน่นของน้ำ

แหล่งที่มา

ช่วง  ทมทิตชงค์ และคณะ. (2537). ฟิสิกส์ 3  ม.5. กรุงเทพฯ:ไฮเอ็ดพับลิชชิ่ง.

โลกต้องจารึก. (มมป.). หลักการของอาร์คิมิดีส. สืบค้นเมื่อ 10 ตุลาคม 2562,  https://www.blockdit.com/articles/5d90d88ed9718d0cbf9214cb

 ความตึงผิว

          จากการที่เราศึกษาเรื่องแรงดันของของเหลว พบว่าของเหลวจะมีแรงดันกระทำในทิศตั้งฉากกับผิวสัมผัสของภาชนะ  ส่วนที่ผิวหน้าของของเหลวเมื่อสัมผัสกับวัตถุอื่น ก็จะเกิดแรงกระทำเหมือนกัน สังเกตได้จากการนำวัตถุที่เป็นของแข็ง เช่น เข็มเย็บผ้า ใบมีดโกน ซึ่งมีความหนาแน่นมากกว่าน้ำหลายเท่าไปวางบนผิวน้ำ ปรากฏว่าเข็มและใบมีดโกนสามารถลอยอยู่บนผิวน้ำได้ แต่เมื่อกดเข็มหรือใบมีดโกนให้จมลงใต้ผิวน้ำ ก็จะจมลงทันทีหรือการที่แมลงตัวเล็ก ๆ สามารถยืนหรือวิ่งไปมาบนผิวน้ำได้ ดังนั้นเราสามารถสรุปได้ว่า ที่ผิวน้ำหรือของเหลวใด ๆ จะต้องมีแรงชนิดหนึ่งที่พยายามยึดผิวของเหลวไว้ ซึ่งเรียกแรงนี้ว่า แรงตึงผิว

ภาพที่ 1 แมลงเดินอยู่บนผิวน้ำ
ที่มา: https://pixabay.com / Free-Photos

          ถ้าเราจะศึกษาลักษณะของแรงตึงผิว ทำได้โดยนำเส้นลวดเส้นเล็ก ๆ มาดัดให้เป็นรูปห่วงวงกลมมีเส้นผ่านศูนย์กลางประมาณ 6 เซนติเมตร แล้วจุ่มโครงลวดนี้ลงในน้ำสบู่ เมื่อดึงลวดขึ้นจากน้ำสบู่จะเห็นฟิล์มของน้ำสบู่ติดอยู่กับโครงลวด นำด้ายเส้นเล็ก ๆ มาผูกเป็นห่วงแล้วค่อย ๆ วางห่วงด้ายลงบนฟิล์มน้ำสบู่ จากนั้นใช้วัสดุปลายแหลมจิ้ม ฟิล์มน้ำสบู่ที่อยู่ภายในห่วงด้ายให้ทะลุ ผลปรากฏว่า ห่วงด้ายมีรูปร่างเป็นวงกลม การที่เป็นเช่นนี้ แสดงว่าแรงตึงผิวของฟิล์มน้ำสบู่ มีทิศขนานกับระนาบของฟิล์มและตั้งฉากกับห่วงเส้นด้าย ดังนั้นจึงสรุปได้ว่า แรงตึงผิวของของเหลวมีทิศขนานกับผิวของของเหลว และตั้งฉากกับเส้นขอบที่ของเหลวสัมผัส

          เราสามารถศึกษา วัดแรงตึงผิวของของเหลวจะใช้อุปกรณ์ที่เรียกว่า ชุดการทดลองวัดแรงตึงผิวของของเหลว โดยจัดอุปกรณ์การทดลองดังนี้

          1. จัดคานของชุดทดลองให้สมดุลอยู่ในแนวระดับแล้วค่อย ๆ เติมน้ำให้แตะด้านล่างของห่วงกลมพอดี

          2. เพิ่มแหวนโลหะลงที่แขวนน้ำหนักจนกระทั่งห่วงวงกลมหลุดจากผิวน้ำพอดี

          3. คำนวณหาแรงซึ่งเป็นแรงที่ใช้ดึงห่วงวงกลมให้หลุดจากผิวน้ำพอดี ซึ่งแรงนี้มีขนาดเท่ากับแรงตึงผิวของน้ำนั่นเองโดยให้หลักของโมเมนต์ เมื่อรู้ mg, x, y

          4. วัดความยาวของเส้นรอบวงของห่วงวงกลมเป็น l คำนวณหาอัตราส่วนระหว่างแรงที่ใช้ดึงกับสองเท่าของความยาวของเส้นรอบวงของห่วงวงกลมหรือ F/2l

          5. เปลี่ยนขนาดห่วงวงกลมอีก 2-3 ขนาด แล้วทำการทดลองซ้ำ แล้วหาค่า F/2l

          6. เปลี่ยนน้ำเป็นของเหลวอื่น ๆ แล้วทำการทดลองซ้ำ ข้อ 1-5

          จากการทดลองจะเห็นว่า เมื่อดึงห่วงวงกลมให้หลุดจากผิวของของเหลวจะพบว่าแรงที่ต้านไม่ให้ห่วงวงกลมหลุดจากผิวของเหลว จะอยู่บริเวณของของเหลว ก่อนที่ห่วงวงกลมจะหลุดจากผิว  ห่วงวงกลมจะดึงผิวของของเหลวขึ้นมาสองผิวคือ ผิวด้านใน และผิวด้านนอกของห่วง ดังนั้น ผิวของของเหลวที่ขาดออกจากกัน จึงมีสองผิว

          จากการศึกษา พบว่า อัตราส่วนระหว่างแรงที่ใช้ดึงห่วงวงกลมกับสองเท่าของความยาวของเส้นรอบวงของห่วงวงกลมสำหรับของเหลวชนิดเดียวกัน อัตราส่วนดังกล่าวจะมีค่าเท่ากัน และจะมีค่าต่างกัน เมื่อเป็นของเหลวต่างชนิดกัน ดังนั้นจึงสรุปได้ว่า สำหรับของเหลวหนึ่ง ๆ อัตราส่วนระหว่างแรงตึงผิวของของเหลวกับความยาวของเส้นผิวของของเหลวที่ขาดมีค่าคงตัว เรียกค่าคงตัวนี้ว่า ความตึงผิว (Surface tension)  ของของเหลว

ความสัมพันธ์ระหว่างงานกับความตึงผิว

          เมื่อนำเส้นลวดเล็ก ๆ มาดัดให้เป็นโครงลวดรูปตัวยูและมีเส้นลวดเล็ก ๆ อีกเส้นหนึ่งวางพาด จากนั้นนำโครงลวดจุ่มลงในน้ำสบู่ เมื่อยกโครงลวดขึ้นจะมีฟิล์มน้ำสบู่ติดขึ้นมาจากนั้นดึงเส้นลวดตรงให้เคลื่อนที่ออกไปตามโครงลวดอย่างช้า ๆ พบว่า ฟิล์มน้ำสบู่จะยืดขยายออก

          ถ้าออกแรงดึงเพิ่มขึ้นเรื่อย ๆ ในที่สุด เส้นลวดตรงจะหลุดจากฟิล์มน้ำสบู่ เมื่อพิจารณาขณะที่เส้นลวดพอดีหลุดจากฟิล์มน้ำสบู่ เมื่อเส้นลวดตรงเลื่อนไปเป็นระยะทำให้ผิวของฟิล์มน้ำสบู่มีพื้นที่เพิ่มขึ้น     ดังนั้น  ความตึงผิวของของเหลวเท่ากับอัตราส่วนระหว่างงานต่อพื้นที่ผิวของเหลวที่เพิ่มขึ้น

หน่วยของความตึงผิวจึงอาจเป็น จูลต่อตารางเมตร

          ค่าความตึงผิวของของเหลวแต่ละชนิดจะมีค่าไม่เท่ากัน สำหรับของเหลวชนิดหนึ่ง ค่าความตึงผิวจะเปลี่ยนไปเมื่อมีสารมาเจือปน เช่น น้ำเกลือ น้ำสบู่ จะมีความตึงผิวน้อยกว่าน้ำ และเมื่ออุณหภูมิเพิ่มขึ้นความตึงผิวของของเหลวจะลดลง

          ดังนั้น สารทั้งหลายประกอบด้วยโมเลกุล เมื่อนำของเหลวบรรจุในภาชนะจะเกิด แรงระหว่างโมเลกุล ซึ่งประกอบด้วยกัน 2 แบบ คือแรงระหว่างโมเลกุลของของเหลวด้วยกัน ซึ่งเป็นโมเลกุลของสารชนิดเดียวกัน เรียกแรงนี้ว่า แรงเชื่อมแน่น (cohesive force)  และแรงระหว่างโมเลกุลของของเหลวกับโมเลกุลของภาชนะซึ่งเป็นแรงระหว่างโมเลกุลของสารต่างชนิดกัน เรียกแรงนี้ว่า แรงยึดติด (adhesive force)

          เมื่อเราเทน้ำและปรอทลงในหลอดทดลองแยกกัน เมื่อของเหลวทั้งสองหยุดนิ่ง  แรงยึดติดระหว่างโมเลกุลของน้ำกับโมเลกุลของหลอดแก้วมากกว่าแรงเชื่อมแน่นระหว่างโมเลกุลของน้ำด้วยกันเอง จึงมีผลทำให้ผิวน้ำที่สัมผัสกับผนังหลอดโค้งขึ้น แต่แรงเชื่อมแน่นระหว่างโมเลกุลของปรอทมากกว่าแรงยึดติดระหว่างโมเลกุลของปรอทกับแก้ว จึงทำให้ผิวปรอทที่สัมผัสกับผนังหลอดโค้งลงและโมเลกุลของปรอทถูกดึงห่างออกจากผนัง ดังนั้นปรอทจึงไม่เปียกผนังของหลอด

          ปรากฏการณ์ที่เกี่ยวข้องกับความตึงผิวที่พบได้อีกเช่นการที่จุ่มหลอดแก้วรูเล็ก ๆ ที่เรียกว่า หลอดรูเล็ก (capillary tube) ซึ่งปลายเปิดทั้งสองข้างลงในของเหลว เช่น น้ำและปรอท พบว่า ระดับน้ำในหลอดแก้วสูงกว่าน้ำภายนอกหลอดแก้ว ส่วนระดับปรอทในหลอดแก้วจะต่ำกว่าระดับปรอทภายนอกหลอด

แหล่งที่มา

นิรันดร์  สุวรัตน์. (2551). ฟิสิกส์ ม.5 เล่ม 1-2. กรุงเทพฯ:พัฒนาศึกษา.

ช่วง  ทมทิตชงค์ และคณะ. (2537). ฟิสิกส์ 3  ม.5. กรุงเทพฯ:ไฮเอ็ดพับลิชชิ่ง.

Kaitoon. (2560).  ความตึงผิว. สืบค้นเมื่อ 10 ตุลาคม 2562,   https://dog-vs-cat.com/7-animals-that-can-walk-on-water-8-2-2019

          จากการศึกษาสมบัติของของเหลวพบว่า เมื่อใช้ช้อนคนของเหลวชนิดต่าง ๆ เช่น น้ำ น้ำเชื่อม น้ำมัน หรือนมข้นหวาน ปรากฏว่าการคนในของเหลวแต่ละชนิดจะต้องใช้แรงคนไม่เท่ากันเป็นเพราะสมบัติอย่างหนึ่งของของเหลวที่เรียกว่า ความหนืด (viscosity) โดยของเหลวที่มีความหนืดมากจะมีแรงต้าน การเคลื่อนที่ของวัตถุในของเหลวนั้นมาก แรงต้านการเคลื่อนที่อันเนื่องมาจากความหนืดของของเหลวนี้ เรียกว่า แรงหนืด (viscous force)

ภาพที่ 1 ความหนืดของน้ำผึ้ง
ที่มา: https://pixabay.com , stevepb

วิธีการเปรียบเทียบความหนืดของของเหลว

          1. ถ้าเรานำของเหลวใส่หลอดหยด แล้วลองหยดดู จะพบว่าของเหลวที่มีความหนืดน้อยจะหยดเร็ว ส่วนของเหลวที่มีความหนืดมากจะหยดช้า

          2. พิจารณาจากการคนของเหลว ถ้าของเหลวมีความหนืดมากจะคนยาก หรือรู้สึกมีแรงต้านจากการคนของเหลวมากแต่ถ้าของเหลวมีความหนืดน้อยจะคนง่ายหรือรู้สึกมีแรงต้านจากของเหลวน้อย

          3. บรรจุของเหลวในหลอดฉีด แล้วออกแรงบีบ จะพบว่าของเหลวที่มีความหนืดน้อยจะพุ่งไปได้ไกลกว่าของเหลวที่มีความหนืดมาก

          4. พิจารณาการปล่อยวัตถุเล็ก ๆ ให้ตกในของเหลว ถ้าของเหลวมีความหนืดน้อยวัตถุจะตกเร็ว แต่ถ้าของเหลวมีความหนืดมาก วัตถุจะตกช้า

          ขณะวัตถุเคลื่อนที่ในของเหลว จะมีแรงกระทำต่อวัตถุ 3 แรงด้วยกัน คือ

          1. น้ำหนักของวัตถุ (mg) ซึ่งมีค่าคงที่เสมอ

          2. แรงดันของของเหลวที่กระทำต่อวัตถุ บางครั้งเรียกแรงลอยตัว ซึ่งมีค่าคงที่

          3. แรงหนืด เป็นแรงต้านการเคลื่อนที่ของของเหลวที่กระทำต่อวัตถุ

          ในช่วง A ไป B วัตถุเคลื่อนลงด้วยความเร่ง (a)

                    จาก 

                    mg – F_หนืด – F_ดัน = ma                        ….. (1)

           ในช่วง B ไป  C วัตถุจะเคลื่อนที่ด้วยความเร็วคงที่ ซึ่งเรียกว่าความเร็วปลาย (terminal velocity)

                    จาก 

                    mg – F_หนืด – F_ดัน = 0                           ….. (2)

                     จาก (1)   F_หนืด = mg – F_ดัน – ma                      .…. (3)

                     จาก (2) F_หนืด =  mg – F_ดัน                                .…. (4)

          ดังนั้น จาก (3), (4)  F_หนืด  จะมีค่าต่างกัน โดยในช่วง B ไป C วัตถุตกลงมาด้วยความเร็วสูงสุด F_หนืด      มีค่ามากกว่าในช่วง A ไป  B ซึ่งมีความเร็วไม่มากนัก  จึงพอสรุปได้ว่า แรงหนืดของของเหลวที่กระทำต่อวัตถุที่เคลื่อนที่ในของเหลวจะขึ้นอยู่กับขนาดของความเร็วในการเคลื่อนที่ของวัตถุ

 กฎของสโตกส์

          เมื่อปล่อยวัตถุทรงกลมตันให้เคลื่อนที่ในของเหลวความหนืด (viscosity) ของของไหลจะทำให้เกิดแรงต้านการเคลื่อนที่ของวัตถุ แรงนี้เรียกว่า แรงหนืด (viscous force) จากการศึกษาของสโตกส์ (Sir George Stokes)  พบว่าแรงหนืดแปรผันตรงกับความเร็วของวัตถุทรงกลมและมีค่าตามสมการต่อไปนี้

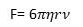
          เมื่อ F  คือ แรงหนืด มีหน่วยเป็น นิวตัน (N)

                r   คือ รัศมีของวัตถุทรงกลมตัน มีหน่วยเป็น เมตร (m)

                v   คือ ความเร็วของวัตถุทรงกลมตัน มีหน่วยเป็น เมตรต่อวินาที (m/s)

              คือ สัมประสิทธิ์ความหนืดของของไหล มีหน่วยเป็น นิวตัน.วินาที/เมตร² (N.s/m²)

          ค่าความหนืดของของไหลบางชนิด ที่อุณหภูมิ 20 องศาเซลเซียส

สารที่มีสถานะเป็นของเหลว เช่น

          กลีเซอรอล                  มีความหนืดเท่ากับ 1412 x 10^-3  N.s/m²

          น้ำมันลินซีด                มีความหนืดเท่ากับ 986 x 10^-3  N.s/m²

          น้ำมันมะกอก               มีความหนืดเท่ากับ 84 x 10^-3  N.s/m²

          กรดซัลฟิวริก               มีความหนืดเท่ากับ 22 x 10^-3  N.s/m²

          เอทิลแอลกอฮอล์           มีความหนืดเท่ากับ 1.192 x 10^-3  N.s/m²

          น้ำ                           มีความหนืดเท่ากับ 1.005 x 10^-3  N.s/m²

          เบนซิน                      มีความหนืดเท่ากับ 0.649 x 10^-3  N.s/m²

          น้ำมันละหุ่ง                 มีความหนืดเท่ากับ 0.234 x 10^-3  N.s/m²

สารที่มีสถานะเป็นแก๊ส เช่น

          ออกซิเจน                   มีความหนืดเท่ากับ 20.9 x 10^-6  N.s/m²

          ฮีเลียม                      มีความหนืดเท่ากับ 18.9 x 10^-6  N.s/m²

          อากาศ                     มีความหนืดเท่ากับ 18.08  x 10^-6  N.s/m²

          คาร์บอนมอนอกไซด์       มีความหนืดเท่ากับ 18.4 x 10^-6  N.s/m²

          คาร์บอนไดออกไซด์       มีความหนืดเท่ากับ 16.0 x 10^-6  N.s/m²

          คลอรีน                      มีความหนืดเท่ากับ 14.7 x 10^-6  N.s/m²

          มีเทน                        มีความหนืดเท่ากับ 12.0 x 10^-6  N.s/m²

          ไฮโดรเจน                   มีความหนืดเท่ากับ 9.5 x 10^-6  N.s/m²

ตารางที่ 1 ความหนืดของของไหลกับอุณหภูมิต่าง ๆ

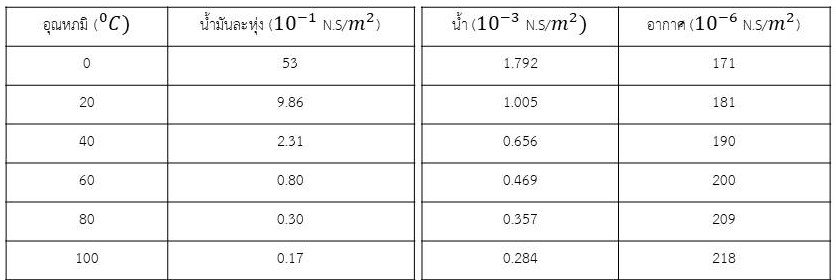
          จากตารางจะพบว่าความหนืดของแก๊สเพิ่มขึ้นเมื่ออุณหภูมิเพิ่มขึ้นและความหนืดของของเหลวจะลดลงเมื่ออุณหภูมิเพิ่มขึ้น

สรุปเกี่ยวกับความหนืด

          1. แรงหนืดขึ้นกับความเร็วของวัตถุที่เคลื่อนที่ในของไหล และขึ้นกับสัมประสิทธิ์ความหนืด

          2. ของเหลวความหนืดสูงจะเคลื่อนที่ได้ช้ากว่าความหนืดต่ำ

          3. สำหรับของเหลว ความหนืดจะมากถ้าอุณหภูมิต่ำ และความหนืดจะน้อยถ้าอุณหภูมิสูง

          4. สำหรับอากาศ ความหนืดจะมากถ้าอุณหภูมิต่ำ และความหนืดจะน้อยถ้าอุณหภูมิสูง

          5. สำหรับอากาศ ความหนืดจะมากถ้าอุณหภูมิสูง และความหนืดจะน้อยถ้าอุณหภูมิต่ำ

          6. ความหนืดของหล่อลื่นบอกได้ด้วยตัวเลข SAE (เอสเออี) ความหนืดมาก ตัวเลข SAE มาก, ความหนืดน้อย ตัวเลข SAE น้อย

ตัวอย่างที่ 1 เมื่อหยดน้ำหมึกลงในของเหลวชนิดหนึ่ง ข้อใดเป็นสาเหตุที่ทำให้หยดน้ำหมึกมีรูปร่างเป็นทรงกลม จงพิจารณาข้อความต่อไปนี้

          A. ความดันของของเหลวมีค่าไม่มากนัก

          B. อุณหภูมิสูง แรงดึงผิวจึงมีค่ามาก

          C. แรงดึงผิวช่วยยึดผิวของของเหลวไว้

          D. ของเหลวมีความหนาแน่นมาก

ข้อใดถูกต้อง

          1. ข้อ A เท่านั้น     2. ข้อ A, C เท่านั้น

          3. ข้อ B, C เท่านั้น 4. ข้อ C, D  เท่านั้น

เฉลย ข้อที่ถูกต้อง คือข้อ 4

ตัวอย่างที่ 2 เมื่อทดลองหย่อนลูกกลมโลหะเล็ก ๆ ก้อนหนึ่งลงในของเหลวต่างชนิดกัน จงพิจารณาข้อความต่อไปนี้ข้อใดถูกต้อง

          1. ความเร็วสุดท้ายของลูกกลมโลหะในของเหลวทุกชนิดมีค่าเท่ากันหมด

          2. ความเร็วสุดท้ายของลูกกลมโลหะในของเหลวที่มีความหนืดสูงมีค่าน้อย

          3. ความเร็วสุดท้ายของลูกกลมโลหะแปรผันตรงกับความหนืดของของเหลว

          4. ความเร็วสุดท้ายของลูกกลมโลหะในของเหลวที่มีความหนืดสูงมีค่ามาก

เฉลย ข้อที่ถูกต้องคือข้อ 2

แหล่งที่มา

คณาจารย์แม็ค. (2551). ฟิสิกส์ ม.5. กรุงเทพฯ:แม็ค.

นิรันดร์  สุวรัตน์. (2551). ฟิสิกส์ ม.5 เล่ม 1-2. กรุงเทพฯ:พัฒนาศึกษา.

A2B Food. (2560).  ความหนืด. สืบค้นเมื่อ 10 ตุลาคม 2562,  จาก http://a2bfood.com/author/admin/

หลักของแบร์นูลลี กล่าวถึงของไหลในอุดมคติ มีข้อกำหนดดังนี้คือ

          1. ของไหลมีการไหลอย่างสม่ำเสมอ ทุกอนุภาคเมื่อเคลื่อนที่ผ่านจุดเดียวกัน จะมีความเร็วเท่ากันเมื่อเคลื่อนที่ผ่านจุดต่างกันจะมีความเร็วเท่ากันหรือต่างกันก็ได้

          2. อนุภาคของของไหลเคลื่อนที่โดยไม่หมุน

          3. ของไหลเคลื่อนที่ไปโดยไม่มีแรงต้านเนื่องจากความหนืด

          4. ของไหลไม่สามารถอัดได้ ไม่ว่าจะไหลผ่านบริเวณใดความหนาแน่นไม่เปลี่ยนแปลง

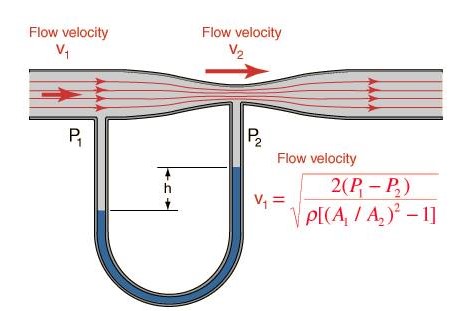
รูปที่ 1 เครื่องมือ เวนจูรี
ที่มา: http://www.rmutphysics.com/charud/oldnews/0/286/15/9/Fluid/fluiddynamic.htm

          ของไหลอุดมคติ เป็นของไหลที่อัดตัวไม่ได้และไม่มีความหนืด มีการไหลสม่ำเสมอ อนุภาคของของไหลแต่ละอนุภาคจะมีเส้นทางการไหลที่แน่นอน ไม่ตัดกัน เรียกว่า สายกระแส (streamline)

          ในของไหลที่ไหลอย่างสม่ำเสมอ อนุภาคหนึ่ง ๆ ของของไหลจะเคลื่อนที่ไปตามเส้นทางเดินเส้นหนึ่งเรียกว่า เส้นกระแส (streamline) โดยความเร็วของอนุภาคที่ตำแหน่งต่าง ๆ มีทิศในแนวเส้นสัมผัส               ณ ตำแหน่ง ดังรูป (a) และเส้นกระแสของอนุภาคแต่ละเส้นจะไม่ตัดกัน ถ้าเส้นกระแสจำนวนหนึ่งอยู่เรียงกันเป็นมัด ดังรูป (b) จะเรียกมัดของเส้นกระแสนี้ว่า หลอดการไหล (tube of flow) หลอดการไหลนี้จึงเปรียบเสมือนท่อที่มีของไหลไหลเข้าทางปลายข้างหนึ่งและไหลออกอีกข้างหนึ่ง

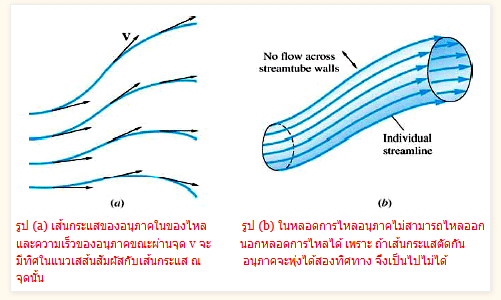
รูปที่ 2 แสดงการไหลในหลอดการไหล
ที่มา: http://theerachot.yolasite.com/

สมการความต่อเนื่อง (The equation of continuity)

          สมการความต่อเนื่องเป็นสมการที่ใช้ศึกษาการไหลของของไหลภายในท่อ การไหลของของไหลในท่อที่มีขนาดสม่ำเสมอไหลจากปลาย [2] ซึ่งมีพื้นที่หน้าตัด A₂ ไปยังปลาย [1] ซึ่งมีพื้นที่หน้าตัด A₁ ดังรูป

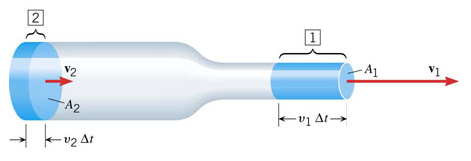
รูปที่ 3 แสดงการไหลอย่างต่อเนื่องของของไหล
ที่มา: http://theerachot.yolasite.com/

                      m₁=m₂

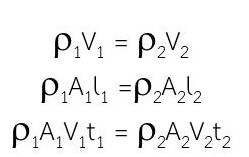
จะได้ว่า    A₁V₁  =   A₂V₂

แต่        , t  เท่ากัน Av คือ อัตราการไหล หน่วยเป็นลูกบาศก์เมตรต่อวินาที      

พลังงานรวมของของเหลว และทฤษฎีบทของเบอร์นูลลี

          การเคลื่อนที่ของของไหลพิจารณาได้จากพลังงานต่าง ๆ ของของไหลนั้น การพิจารณาเกี่ยวกับพลังงานของวัตถุไม่ว่าวัตถุนั้นจะอยู่ในสภาวะเช่นใด อาจมีพลังงานหลายอย่างแต่ผลบวกของพลังงานเหล่านี้จะมีค่าคงตัวเสมอ

          1. พลังงานศักย์ ถ้าของเหลวอยู่สูงจากระดับสมมติอันหนึ่ง

             พลังงานศักย์ = mgh

             พลังงานศักย์ต่อมวลสารของของเหลว = mgh/m = gh

          2. พลังงานความดัน เราสามารถหาค่าพลังงานนี้โดยการพิจารณาจากการเปลี่ยนแปลงสภาพของ พลังงานศักย์มาเป็นพลังงานชนิดนี้

             ความดันของของเหลว  = (ความหนาแน่น)(ค่าความเร่งเนื่องจากแรงโน้มถ่วง)(ความสูง)

          3. พลังงานจลน์ ถ้าของเหลวเคลื่อนที่อยู่ด้วยความเร็ว พลังงานจลน์ของมวลสาร = 1/2 mv²

ดังนั้น พลังงานจลน์ต่อมวลสาร = (1/2mv²)/m = v²/2

ตัวอย่าง 1 เม็ดเลือดไหลด้วยอัตราเร็ว 8 เซนติเมตรต่อวินาที ในเส้นเลือดใหญ่มีรัศมี 0.6เซนติเมตร ไปสู่เส้นเลือดขนาดเล็กลง และมีรัศมี 0.3 เซนติเมตร อัตราเร็วของเม็ดเลือดในเส้นเลือดเล็กเป็นกี่เซนติเมตรต่อวินาที

วิธีทำ                                      จาก Av = ค่าคงตัว
                                         จะได้ A₁v₁ = A₂v₂

        (22/7)(0.6 cm)(0.6 cm)(8 cm/s) = (22/7)(0.3 cm)(0.3 cm)v₂
                                                     v₂ = 32 cm/s
        ตอบ อัตราเร็วของเม็ดเลือดในเส้นเลือดเล็กเป็น 32 เซนติเมตรต่อวินาที

สมการของแบร์นูลลี
        พิจารณาหลอดการไหลที่มีระดับต่างกัน และมีพื้นที่หน้าตัดไม่เท่ากัน

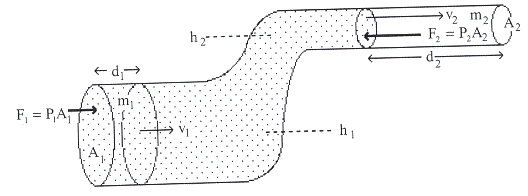
รูปที่ 4 หลอดการไหลที่มีระดับต่างกัน
ที่มา : http://theerachot.yolasite.com/

          แรงดันที่ท่อด้านล่าง  แรงดันที่ท่อด้านบน  และแรงโน้มถ่วง แรงทั้งหมดจะทำให้เกิดงานเนื่องจากของไหล  จากทฤษฎีของงาน – พลังงานงานทั้งหมดที่เกิดจากการเคลื่อนที่ของของไหลส่วนเล็ก ๆ ที่พิจารณา  จะมีค่าเท่ากับการเปลี่ยนแปลงพลังงานจลน์ของมวลที่เคลื่อนที่

                    F₁d₁ – F₂d₂ –mg(h₂ – h₁) = 1/2mv₂² -1/2mv₁²

จากนิยามของความดันและความหนาแน่น

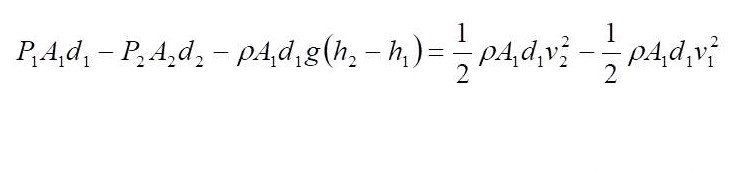
เมื่อปริมาตรของไหลส่วนที่เคลื่อนที่ในท่อล่างกับท่อบนมีค่าเท่ากัน

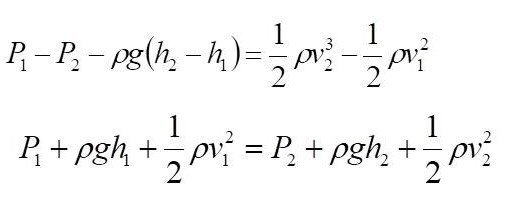
สมการที่ได้เรียกว่าสมการแบร์นูลลี  นั่นคือ

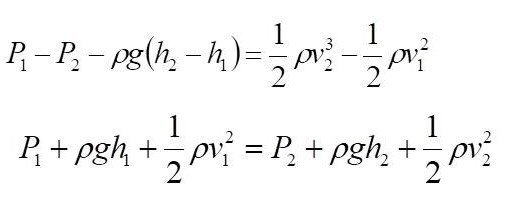                                        =        ค่าคงที่

ตัวอย่างที่ 2 ข้อใดกล่าวผิดเกี่ยวกับหลักการของแบร์นูลลี

          1. ของไหลเคลื่อนที่โดยไม่มีการหมุน

          2. ของไหลมีการเคลื่อนที่โดยไม่มีแรงต้านในของไหล

          3. ของไหลเคลื่อนที่โดยมีความหนาแน่นคงตัว

          4. ของไหลมีความดันเพิ่มขึ้นเมื่อมีอัตราเร็วเพิ่มขึ้น

เฉลย ข้อที่ถูกต้อง คือ ข้อ 4

ตัวอย่างที่ 3 จากข้อมูลต่อไปนี้

          A. อัตราการไหลของน้ำจะเพิ่มขึ้นเมื่อพื้นที่หน้าตัดของหลอดการไหลลดลง

          B. เมื่อพื้นที่หน้าตัดของหลอดการไหลเพิ่มขึ้นความดันของของไหลจะลดลง

          C. ความเร็วของน้ำที่ไหลผ่านท่อที่มีขนาดเล็กลงจะเร็วขึ้น

          D. สมการความต่อเนื่องบอกให้ทราบถึงอัตราของมวลที่ไหล

ข้อใดที่ถูกต้อง

          1. ข้อ A, B, C และ D    2. ข้อ A, B และ C

          3. ข้อ A และ C             4. ข้อ C และ D 

เฉลยข้อที่ถูกต้องคือข้อ 4

ตัวอย่างที่ 4 จงพิจารณาข้อความต่อไปนี้ข้อใดถูกต้อง

          1. พื้นที่หน้าตัดของท่อลดลง อัตราเร็วของไหลเพิ่มขึ้น ความดันในของไหลลดลง

          2. พื้นที่หน้าตัดของท่อลดลง อัตราเร็วของไหลลดลง ความดันในของไหลลดลง

          3. พื้นที่หน้าตัดของท่อเพิ่มขึ้น อัตราเร็วของไหลลดลง ความดันในของไหลลดลง

          4. พื้นที่หน้าตัดของท่อเพิ่มขึ้น อัตราเร็วของไหลเพิ่มขึ้น ความดันในของไหลลดลง

เฉลยข้อที่ถูกต้อง คือ ข้อ 1

ตัวอย่างที่ 5 จากการไหลของของไหลในอุดมคติและหลักการของแบร์นูลลี พบว่าถ้าที่บริเวณใดมีอัตราเร็วของของไหลเพิ่มขึ้น แสดงว่า

          A. พื้นที่บริเวณนั้นมีขนาดเล็กลง B. พื้นที่บริเวณนั้นมีขนาดเพิ่มขึ้น

          C. ความดันของของไหลลดลง   D. ความดันของของไหลเพิ่มขึ้น

คำกล่าวที่ถูกต้องคือข้อใด

          1. ข้อ A และ C          2. ข้อ A และ D

          3. ข้อ B และ C          4. ข้อ B และ D 

เฉลยข้อที่ 1

แหล่งที่มา

ช่วง  ทมทิตชงค์ และคณะ. (2537). ฟิสิกส์ 3  ม.5. กรุงเทพฯ:ไฮเอ็ดพับลิชชิ่ง.

ภาควิชาฟิสิกส์ มหาวิทยาลัยเทคโนโลยีราชมงคล. (มมป.). พลศาสตร์ของไหล. สืบค้นเมื่อ 10 ตุลาคม 2562,   http://www.rmutphysics.com/charud/oldnews/0/286/15/9/Fluid/fluiddynamic.htm