ค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก

หลายๆคนที่เคยเรียนวิชาฟิสิกส์ คงจะรู้จักค่า g หรือ ค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก ซึ่งในตอนที่เรียนนั้น จะมีการใช้งานอยู่ 2 ค่า คือ g = 10 m/s2และ g = 9.81 m/s2คำถามต่อมาก็ คือ แล้วค่า g จริงๆแล้วมีค่าเท่าไร และมีที่มาอย่างไร

ในความเป็นจริงแล้ว ค่า g ไม่ใช่ซึ่งค่าคงที่ในทุกๆต่ำแหน่งบนโลก แต่จะมีค่าแปรแปลี่ยนไปตามภูมิประเทศต่างๆ บนโลก

ค่า g นี้สามารถเขียนเป็นสมการความสัมพันธ์ได้ดัง กฎความโน้มถ่วงของนิวตัน (Newton’s Law of Graitation) ได้ดังนี้
g =GM/R2

เมื่อ

g = ค่าความเร่งเนื่องจากแรงโน้มถ่วง

G = ค่าคงตัวโน้มถ่วงสากล (Uniersal graitational constant)= 6.67×10- 11นิวตัน(เมตร)2/(กิโลกรัม)2

M = มวลของโลก = 5.98 x 1024กิโลกรัม

R = รัศมีของโลก = 6.37×106
จากสมการที่ใช้ในการหาค่า g จะพบว่า ค่า g จะแปรผกผันกับค่า R หรือรัศมีระหว่างจุดศูนย์กลางของโลกกับจุดที่คุณต้องการหาค่า g นั่นแสดงว่า ถ้าคุณต้องการค่า g มากที่สุด ก็ต้องหาว่าบริเวณใดที่อยู่ต่ำกว่า ระดับน้ำทะเลมากๆ หรือ มีค่า R น้อยๆ นั่นเอง ในกรณีนี้ผมมีข้อมูลว่า ในประเทศสหรัฐอเมริกามีจุดที่ต่ำที่สุดอยู่ที่ Death alley คือ -282 ft (-85.9536m) สามารถคำนวณหาค่า g ได้ดังนี้

จากสมการ g =GM/R2

แทนค่าต่างๆ ได้

g =((6.673×10- 111)(5.98×1024))/(6.37×106– 85.9536)2

g =9.834565215 m/s2
ลองเปรียบเทียบกับค่า g ที่ได้จากการคำนวณจากค่า R = 6.37×106คือ 9.834299811 m/s2โดยมีค่าที่แตกต่างกันประมาณ 0.000265404 m/s2ซึ่งจะพบว่าค่าที่แตกต่างกันนี้ไม่มีผลมากนักในการคำนวณ หรือจะเรียกได้ว่า ตัดทิ้งได้ ดังนั้นในการใช้งานค่า g จริงๆ แล้ว ควรใช้ที่ค่า g = 9.83 m/s2น่าจะถูกต้องกว่า แต่ก็ขึ้นอยู่กับว่า สิ่งที่เรากำลังคำนวณนั้นต้องการความละเอียดแค่ไหน
ในกรณีของประเทศไทย หากคุณต้องการทราบค่า g ที่สูงที่สุด หรือต้องการทราบค่า g ที่บริเวณที่ คุณอยู่ ก็ต้องทราบว่าที่ๆ คุณอยู่ตอนนี้มีความสูง ของพื้นที่เป็นอย่างไร สูงหรือต่ำกว่าระดับน้ำทะเล เท่าไร ลองคำนวณดูได้เลยครับ

ที่มา :http://mengineer.wordpress.com

ประวัติการค้นพบค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก

แรกเริ่มเดิมทีนั้น มนุษย์เชื่อว่า "เมื่อปล่อยวัตถุสองชิ้นซึ่งมีมวลต่างกันจากที่สูงเท่ากันพร้อมๆกันภายใต้แรงโน้มถ่วงของโลก วัตถุที่มีมวลมากกว่าจะตกถึงพื้นก่อน" ซึ่งความคิดนี้ถูกนำเสนอไว้โดย"อริสโตเติล" นักปราชญ์ชาวกรีก ซึ่งความคิดนี้ได้รับการยอมรับ และเชื่อถือต่อมาอีกหลายร้อยปีโดยปราศจากการทดลอง ตรวจสอบหรือแม้แต่กาตั้งคำถามถึงความถูกต้อง

กาลิเลโอ กาลิเลอี กับการทดลอง ณ หอเอนเมืองปิซ่า

รูปปั้น กาลิเลโอ เมืองฟลอเรนซ์ ประเทศอิตาลี

การศึกษาถึงทฤษฎีความโน้มถ่วงสมัยใหม่ได้ถูกนำเสนอเป็นครั้งแรกโดย กาลิเลโอ กาลิเลอี (Galileo Galilei ค.ศ. 1564 - 1642 ) ในช่วงปลายทศวรรษที่ 16 การทดลองที่มีชื่อเสียงของกาลิเลโอ คือ การทดลองปล่อยวัตถุที่มีมวลต่างกัน 2 ชิ้น จากยอดหอเอนปิซา ในเวลาพร้อมกัน ซึ่งวัตถุดังกล่าว ได้ตกลงมาภายใต้แรงโน้มถ่วงโลก และถึงพื้นเกือบจะพร้อมๆ กัน ซึ่งเป็นการพิสูจน์ว่าความคิดของอริสโตเติลนั้นไม่ถูกต้อง (ในปัจจุบันยังเป็นที่ถกเถียงกันว่ากาลิเลโอได้ทำการทดลองดังกล่าวจริงหรือเป็นเพียงการทดลองเชิงความคิด) กาลิเลโอได้แสดงให้เห็นว่าวัตถุที่เคลื่อนที่ภายใต้แรงโน้มถ่วงของโลกนั้นจะเคลื่อนที่โดยมีความเร่งเท่ากันไม่ว่าวัตถุนั้นจะมีมวลเท่าใดก็ตาม

รูปหอเอนเมืองปิซ่า ประเทศอิตาลี

กฎแรงดึงดูดระหว่างมวลของนิวตัน

รูปปั้นของเซอร์ไอแซค นิวตัน ภายในมหาวิทยาลัยเคมบริดจ์

เซอร์ไอแซก นิวตัน(Sir Isaac Newton ค.ศ. 1642 - 1726) นักคณิตศาสตร์และนักฟิสิกส์ชาวอังกฤษ เป็นบุคคลที่มีส่วนสำคัญในการศึกษาเกี่ยวกับแรงโน้มถ่วงเป็นอย่างมาก ทฤษฎีที่ทำให้เขามีชื่อเสียงมากที่สุด คือ การค้นพบกฎแรงดึงดูดของโลก (Law of Graitation) ซึ่งเขาได้ค้นพบทฤษฎีโดยบังเอิญ เหตุการณ์เกิดขึ้นในวันหนึ่งขณะที่นิวตันกำลังนั่งดูดวงจันทร์ แล้วก็เกิดความสงสัยว่าทำไมดวงจันทร์จึงต้องหมุนรอบโลก ในระหว่างที่เขากำลังนั่งมองดวงจันทร์อยู่เพลิน ๆ ก็ได้ยินเสียงแอปเปิ้ลตกลงพื้น เมื่อนิวตันเห็นเช่นนั้นก็ให้เกิดความสงสัยมากขึ้นไปอีกว่า ทำไมวัตถุต่าง ๆ จึงต้องตกลงสู่พื้นดินเสมอทำไมไม่ลอยขึ้นฟ้าบ้าง ซึ่งนิวตันคิดว่าต้องมีแรงอะไรสักอย่างที่ทำให้แอปเปิ้ลตกลงพื้นดิน จากความสงสัยข้อนี้เอง นิวตันจึงเริ่มการทดลองเกี่ยวกับแรงโน้มถ่วงของโลก การทดลองขั้นแรกของนิวตัน คือ การนำก้อนหินมาผูกเชือก จากนั้นก็แกว่งไปรอบ ๆ นิวตันสรุปจากการทดลองครั้งนี้ว่าเชือกเป็นตัวการสำคัญที่ทำให้ก้อนหินแกว่งไปมารอบ ๆ ไม่หลุดลอยไป ดังนั้นสาเหตุที่โลก ดาวเคราะห์ ต้องหมุนรอบดวงอาทิตย์ และดวงจันทร์ต้องหมุนรอบโลกต้องเกิดจากแรงดึงดูดที่ดวงอาทิตย์ที่มีต่อโลก และดาวเคราะห์ และแรงดึงดูดของโลกที่ส่งผลต่อดวงจันทร์ รวมถึงสาเหตุที่แอปเปิ้ลตกลงพื้นดินด้วยก็เกิดจากแรงดึงดูดของโลกด้วย

งานเขียนในปี ค.ศ. 1687 เรื่อง Philosophiae Naturalis Principia Mathematica (เรียกกันโดยทั่วไปว่าPrincipia) ถือเป็นหนึ่งในหนังสือที่มีอิทธิพลที่สุดในประวัติศาสตร์วิทยาศาสตร์ เป็นรากฐานของวิชากลศาสตร์ดั้งเดิม ในงานเขียนชิ้นนี้ นิวตันพรรณนาถึง กฎแรงโน้มถ่วงสากลและ กฎการเคลื่อนที่ของนิวตันซึ่งเป็นกฎทางวิทยาศาสตร์อันเป็นเสาหลักของการศึกษาจักรวาลทางกายภาพตลอด ช่วง 3 ศตวรรษถัดมา นิวตันแสดงให้เห็นว่า การเคลื่อนที่ของวัตถุต่างๆ บนโลกและวัตถุบนท้องฟ้าล้วนอยู่ภายใต้กฎธรรมชาติชนิดเดียวกัน โดยแสดงให้เห็นความสอดคล้องระหว่างกฎการเคลื่อนที่ของดาวเคราะห์ของเคปเลอร์ กับทฤษฎีแรงโน้มถ่วงของตน ซึ่งช่วยยืนยันแนวคิดดวงอาทิตย์เป็นศูนย์กลางจักรวาล และช่วยให้การปฏิวัติวิทยาศาสตร์ก้าวหน้ายิ่งขึ้น

รูปหนังสือ Philosophiae Naturalis Principia Mathematica

ข้อความส่วนหนึ่งในหนังสือ The Principia ซึ่งกล่าวถึงแรงดึงดูดระหว่างมวลมีดังนี้ “I deduced that the forces which keep the planets in their orbs must [be] reciprocally as the squares of their distances from the centers about which they reole: and thereby compared the force requisite to keep the Moon in her Orb with the force of graity at the surface of the Earth; and found them answer pretty nearly.” และหากพิจารณาถึงแรงดึงดูดระหว่างมวลตามแนวคิดนี้ จะได้ว่า แรงดึงดูดระหว่างมวลนั้นจะมีค่าแปรผันตรงกับขนาดของมวลทั้งสอง และแปรผกผันกับค่ากำลังสองของระยะห่างระหว่างจุดศูนย์กลางมวลทั้งสอง

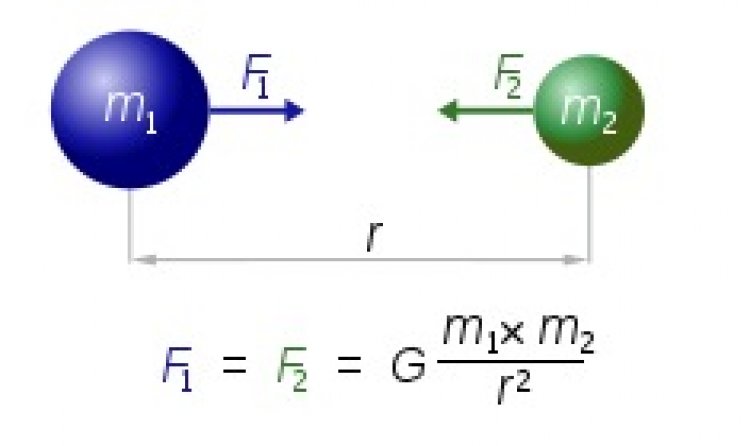
เมื่อ F1และ F2คือ แรงดึงดูดระหว่างมวลทั้งสอง m1และ m2คือมวลของวัตถุทั้งสอง r คือ ระยะห่างระหว่างจุกศูนย์กลางมวลทั้งสอง ส่วน G คือค่าคงที่ หรือ Uniersal constant of graity ซึ่งมีค่าประมาณ6.674×10−11
N m2kg−2

นิวตันเองนั้นไม่ได้ระบุค่า G หรือค่า Uniersal constant of graity ในการตีพิมพ์งานของเขา ค่า G ที่เราใช้อยู่ในปัจจุบันนั้นเป็นค่าที่ถูกค้นพบหรือคำนวณออกมาภายหลังการตีพิมพ์หนังสือ The Principia ถึง 111 ปี หรือ 71 ปีหลังจากการเสียชีวิตของนิวตัน โดยเป็นผลงานของ เฮนรี คาเวนดิช(Henry Caendish) ในปี ค.ศ. 1798 ซึ่งคาเวนดิชเองก็ไม่ได้ตั้งใจจะหาค่า G โดยตรง แต่เขาได้ทำการทดลองเพื่อทดสอบกฎแรงดึงดูดระหว่างมวลของนิวตัน โดยได้แขวนดัมเบล (dumb-bell) ที่ทำด้วยตะกั่วและมีขนาดเล็ก ด้วยเส้นด้าย แล้วให้ดัมเบลนี้อยู่ระหว่างมวลที่มีขนาดใหญ่เท่าลูกโบว์ลิ่ง 2 ลูก แรงดึงดูดแบบโน้มถ่วงระหว่างดัมเบลลูกหนึ่งกับมวลขนาดใหญ่ก้อนหนึ่งจะทำให้เส้นด้ายบิดตัวไปเล็กน้อย ดังนั้นเมื่อ Caendish วัดมุมที่เส้นด้ายบิดตัวไป รู้มวลของดัมเบลรวมทั้งมวลขนาดใหญ่และแรงโน้มถ่วงที่เกิดขึ้นระหว่าง ดัมเบลกับมวล เขาก็สามารถรู้ค่า G ได้ นับตั้งแต่วันนั้นจนกระทั่งถึงวันนี้ นักฟิสิกส์ได้พยายามปรับปรุงวิธีการวัดค่า G ให้ละเอียดขึ้นและถูกต้องยิ่งขึ้น เช่น ได้เปลี่ยนแปลง เส้นด้ายของ Caendish เป็นลวดที่ทำด้วยทังสเตนหรือควอทซ์ ดังนั้น เวลานำมวลขนาดใหญ่มาดึงดูดดัมเบล แรงดึงดูด จะทำให้ลวดบิดตัวไปเล็กน้อย เหตุการณ์ที่ตามมาเวลาเอามวลขนาดใหญ่ออกไปไกลๆ คือลวดจะบิดตัวกลับที่เดิมทันที จังหวะการแกว่งตัวไปมาของดัมเบลเช่นนี้ สามารถช่วยให้เรารู้ค่า G ได้

การหาค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก ด้วยการแกว่งของลูกตุ้มอย่างง่าย

สำหรับนักเรียนที่ต้องเรียนฟิสิกส์แล้ว ค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลกหรือค่า g นั้น เป็นค่าที่ต้องใช้ในการคำนวณบ่อยครั้ง โดยเฉพาะเรื่องการเคลื่อนที่ภายใต้แรงโน้มถ่วงของโลก แต่ใครจะทราบบ้างว่าค่า g สามารถหาได้อย่างไร ซึ่งการทดลองเพื่อหาค่า g นั้นมีได้หลายวิธีและก็ไม่ได้ยุ่งยาก ดังเช่น ตัวอย่างการทดลองที่นำเสนอในองค์ความรู้นี้ก็เป็นหนึ่งในการทดลองที่สามารถนำไปสู่การหาค่า g ได้ การทดลองที่ว่านั้นคืออะไร ทดลองอย่างไร และหาค่า g ได้อย่างไร ลองติดตามกันครับ

รูปแสดงอุปกรณ์การทดลองลูกตุ้มอย่างง่าย

ทฤษฎีและหลักการ

เมื่อพิจารณาการแกว่งของลูกตุ้มอย่างง่าย ในกรณีที่แอมพลิจูดน้อยๆ จะสามารถประมาณการแกว่งได้ว่าเป็นการแกว่งแบบซิมเปิลฮาร์มอนิก และคาบของการแกว่งจะสัมพันธ์กับความยาวของลูกตุ้ม (L) ตามสมการ

เมื่อ L คือ ระยะจากจุดตรึงไปยังศูนย์กลางของมวล, g คือ ค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก และ T คือคาบการแกว่ง

อุปกรณ์การทดลอง

1. ลูกตุ้ม

2. เชือก

3. ขาตั้งสำหรับแขวนลูกตุ้ม

4. ไม้เมตรหรือตลับเมตร

5. นาฬิกาจับเวลา

6. กระดาษกราฟหรือคอมพิวเตอร์พร้อมโปรแกรม MS Excel

การทดลอง

1. วัดความยาวเชือกที่แขวนลูกตุ้ม (L) (ความยาวเชือกบวกกับรัศมีของลูกตุ้ม) จัดให้ลูกตุ้มแกว่งโดยมีมุมแกว่งไม่เกิน 5 องศา

2. จับเวลาที่ลูกตุ้มแกว่งครบ 10 รอบ คำนวณค่าคาบการแกว่งเฉลี่ยของลูกตุ้ม (T)

3. ทำการทดลองซ้ำข้อ 1-2 โดยเปลี่ยนค่าความยาวของลูกตุ้ม จบครบ 10 ครั้ง ที่ความยาวต่างๆกัน

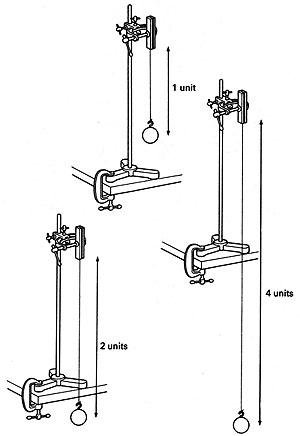
รูปแสดงการเปลี่ยนค่าความยาวของลูกตุ้ม

4. คำนวณหาค่าคาบกำลังสอง (T2) เชียนกราฟเส้นตรงระหว่าง T2(แกนตั้ง) และ L(แกนนอน) ในกระดาษกราฟหรือในโปรแกรม Microsoft Excel และหาค่าความชันของกราฟ

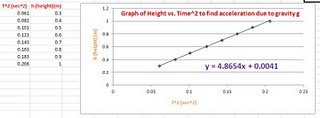
รูปแสดงการหาค่าความชันของกราฟจากโปรแกรม MS Excel

5. จากความชันของกราฟ คำนวณค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก จากสมการ

หรือทำการทดลอง online ได้ที่หน้าเว็บการทดลองเสมือนของมหาวิทยาลัยเทคโนโลยีราชมงคล ตามลิงค์นะครับ

http://www.rmutphysics.com/charud/virtualexperiment/simplependulum2/pendulum2.html

เพียงการทดลองง่ายๆ แค่นี้เราก็สามารถจะทราบได้ว่าบริเวณที่เราอยู่นั้นมีค่า g เป็นเท่าไหร่ หรือใครอาจจะต่อยอดความคิดเป็นโครงงานการสำรวจค่า g ในบริเวณที่ต่างๆกันก็สามารถทำได้นะครับ ลองหลับตาแล้วจินตนาการกันต่อไปว่าเราสามารถจะต่อยอดความรู้นี้ได้อย่างไรอีกบ้างนะครับ

กฎความโน้มถ่วงของนิวตัน 

ตัวอย่างแรงโน้มถ่วงที่เราน่าจะคุ้นเคยมากที่สุดก็คือ"น้ำหนัก"นะครับ ซึ่งก็คือแรงที่ดึงดูดคุณเข้าหาโลก ในระหว่างการศึกษาการเคลื่อนที่ของดาวเคราะห์และดวงจันทร์ นิวตันได้ค้นพบธรรมชาติพื้นฐานของแรงดึงดูดระหว่างวัตถุใดๆ สองวัตถุ นิวตันตีพิมพ์กฎความโน้มถ่วงพร้อมกับกฎการเคลื่อนที่ 3 ข้อของเขาในปี ค.ศ. 1687 เราอาจแถลงกฎนี้ได้ดังนี้ :

"ทุกอนุภาคสสารในเอกภพดึงดูดทุกอนุภาคอื่นด้วยแรงซึ่งแปรผันตรงกับผลคูณของมวลของอนุภาคและแปรผันกับกำลังสองของระยะห่างระหว่างอนุภาคทั้งสองนั้น"

เมื่อแปลข้อความนี้เป็นสมการจะได้ว่า

โดย Fgคือ ขนาดของแรงโน้มถ่วงซึ่งทำต่ออนุภาคใดอนุภาคหนึ่ง, m1และ m2เป็นมวลของอนุภาคทั้งสอง, r คือระยะห่างระหว่างอนุภาคทั้งสอง และ G คือค่าคงตัวฟิสิกส์พื้นฐานที่เรียกว่า ค่าคงตัวโน้มถ่วง

ข้อควรระวัง: เนื่องจาก g และ G เป็นสัญลักษณ์ที่มักจะใช้ในเรื่องความโน้มถ่วง จึงมักจะเกิดความสับสนระหว่างปริมาณโน้มถ่วงที่สัญลักษณ์สองตัวนี้แทน โดย g คือความเร่งเนื่องจากความโน้มถ่วง ค่าของ g นั้น มีค่าต่างกันที่ตำแหน่งซึ่งต่างกันบนผิวโลกและต่างกันบนผิวของดาวเคราะห์ต่างกัน ในทางตรงกันข้าม G ให้ความสัมพันธ์ของแรงโน้มถ่วงระหว่างวัตถุใดๆ สองวัตถุ กับมวลของวัตถุและระยะห่างระหว่างวัตถุ เราเรียก G ว่า "ค่าคงตัวสากล" เพราะปริมาณนี้มีค่าเดียวไม่ว่าวัตถุจะอยู่ตำแหน่งใดในอวกาศ

แรงโน้มถ่วงกระทำในแนวเส้นตรงที่เชื่อมระหว่างอนุภาคทั้งสองและเป็นแรงที่ดึงดูดกันเสมอ แรงสองแรงซึ่งทำที่แต่ละอนุภาคเป็นคู่แรงกิริยา-ปฏิกิริยา แม้แต่เมื่อมวลของอนุภาคต่างกัน แรงสองแรงนี้ก็ยังมีขนาดเท่ากัน แรงดึงดูดที่ตัวเราทำต่อโลกก็มีขนาดเท่ากับขนาดของแรงที่โลกดึงดูดตัวเรา (ฟังดูยิ่งใหญ่ดีมั้ยครับ...) เมื่อแรงที่เราดึงดูดโลก และโลกดึงดูดเรามีขนาดเท่ากัน จึงนำมาซึ่งประเด็นคำถามที่น่าคิด ดังนี้ครับ .......... ในขณะที่เรากระโดดจากกระดานสปริงลงในสระว่ายน้ำ แรงดึงดูดจากโลกดึงดูดให้เราตกลงในสระน้ำ หรือว่าอันที่จริงแล้ว แรงดึงดูดจากตัวเราดึงดูดให้สระว่ายน้ำ(พร้อมโลก) ลอยขึ้นมาชนตัวเรากันแน่????

เราได้แถลงกฎความโน้มถ่วงในรูปของแรงระหว่างอนุภาคสองอนุภาค แต่ปรากฎว่าแรงโน้มถ่วงระหว่างวัตถุสองวัตถุใดๆที่มีมวลกระจายอย่างสมมาตรทรงกลม เช่น ทรงกลมตัน จะมีค่าเหมือนกับว่ามวลทั้งหมดไปรวมกันที่จุดศูนย์กลาง ดังนั้น ถ้าเราจำลองโลกเป็นวัตถุสมสาตรทรงกลมที่มีมวล mEแรงที่โลกกระทำต่ออนุภาคหรือวัตถุสมมาตรทรงกลมที่มีมวล m และมีระยะห่าง r ระหว่างจุดศูนย์กลาง คือ

โดยมีเงื่อนไขว่า วัตถุนั้นอยู่นอกโลก ในขณะเดียวกันวัตถุนั้นก็ออกแรงกระทำต่อโลกขนาดเดียวกัน ที่ผ่านมาเรามักจะกล่าวถึงเรื่องแรงดึงดูด หรือกฎความโน้มถ่วงกันเพียงเท่านี้ แต่ถ้าพิจารณาถึงแรงโน้มถ่วงที่กระทำต่อวัตถุที่อยู่ภายในโลกล่ะครับ กฎความดน้มถ่วงจะมีหน้าตาเปลี่ยนแปลงไปอย่างไร?

ถ้าเราเจาะรูลงใปยังจุดศูนย์กลางของโลกและวัดแรงโน้มถ่วงซึ่งทำต่อวัตถุที่ระดับความลึกต่างๆกัน เราจะพบว่าเมื่อวัตถุเคลื่อนที่เข้าหาจุดศูนย์กลางโลก แรงจะมีขนาดลดลงแทนที่จะเพิ่มชึ้นตามค่า 1/r2ทั้งนี้เพราะเมื่อวัตถุอยู่ภายในเนื้อโลก มวลของโลกบางส่วนซึ่งอยู่ฝั่งตรงข้ามกับจุดศูนย์กลางโลกจะออกแรงดึงวัตถุในทิศตรงกันข้าม และแรงโน้มถ่วงของโลกต่อวัตถุมีค่าเป็นศูนย์ที่จุดศูนย์กลางโลกพอดี

ยังมีจุดสังเกตุที่น่าสนใจอีกประการหนึ่งเกี่ยวกับความโน้มถ่วง นั่นก็คือ รูปทรงของวัตถุส่วนใหญ่ในอวกาศ ทั้งดาวฤกษ์อย่างดวงอาทิตย์ หรือดาวเคราะห์ต่างๆ จึงมักจะมีแนวโน้มเป็นทรงกลม ทั้งนี้เนื่องจากอนุภาคในวัตถุต่างออกแรงดึงดูดระหว่างกัน อนุภาคมีแน้วโน้มที่จะเคลื่อนที่เพื่อทำให้ระยะระหว่างกันมีค่าน้อยที่สุด ผลก็คือ วัตถุมีแนวโน้มที่จะเป็นทรงกลม ปรากฏการณ์นี้มีผลลดลงอย่างมากสำหรับวัตถุในอวกาศที่มีมวลต่ำเพราะแรงโน้มถ่วงจะมีขนาดน้อยกว่า วัตถุเหล่านี้จึงมีแน้วโน้มไม่เป็นทรงกลม เช่น ดาวเคราะห์น้อย

รูปแสดง รูปทรงของดวงอาทิตย์และดาวเคราะห์น้อย Gaspra

ดวงอาทิตย์มีมวลประมาณ 1.9 x 1030kg ซึ่งสูงมากพอที่ทำให้แรงโน้มถ่วงดึงดวงอาทิตย์ให้มีรูปร่างเกือบเป็นทรงกลมรัศมี 696,000 km ในขณะที่ดาวเคราะห์น้อย Gaspra มีมวลเพียง 1016kg เท่านั้น (น้อยมากเมื่อเทียบกับดวงอาทิตย์) แรงโน้มถ่วงระหว่างส่วนต่างๆของดาวเคราะห์น้อยจึงไม่สามารถเอาชนะแรงระหว่างอะตอมได้ รูปร่างของดาวเคราะห์น้อย Gaspra จึงไม่เป็นทรงกลมสม่ำเสมอ