บทความคณิตศาสตร์ประยุกต์ชิ้นนี้มีความประสงค์จะเผยแพร่ความรู้เบื้องตันเกี่ยวกับการหาค่าเหมาะสมเมื่อมีหลายวัตถุประสงค์ (Multiobjective Optimization Problem) เหมาะสำหรับนักเรียนมัธยมศึกษาตอนปลาย ครู และผู้สนใจทั่วไป

ที่มาhttps://www.googe.co.thv/maps/dir/The+Grand+Palace,+Na+Phra+Lan+Rd.+Phra+Nakhon.+Bangkok.+10200/คณะวิทยาศาสตร์+มหาวิทยาลัยมหิดล+Thanon+Rama+Vi+กรุงเทพมหานคร

            Optimization มีรากศัพท์เดียวกันกับคำ optimal ซึ่งหมายความว่า "ดีที่สุด" ดังนั้นเมื่อใดก็ตามที่เราทำ optimization นั่นหมายถึงเราต้องการจะหาค่าดีที่สุด (เหมาะสมที่สุด) ทุกวันเราต้องเผชิญกับการแก้ปัญหาหาคู่เหมาะสมที่สุดเป็นประจำยกตัวอย่างเช่น เวลาเปิด google mapเพื่อค้นหาเส้นทางที่จะนำเราไปยังสถานที่ต่าง ๆ โดยใช้เวลาน้อยที่สุด หรือแม้กระทั่งในขณะนี้ ผู้อ่านอาจจะคิดว่าควรอ่านบทความนี้ให้จบ หรือเอาเวลาไปทำกิจกรรมอื่นเพื่อที่จะใช้เวลาให้คุ้มค่ามากที่สุด

            ในการแก้ปัญหาค่าเหมาะสมนั้น เราสามารถกำหนดวัตถุประสงค์หลายวัตถุประสงค์ได้ เช่น การตัดสินใจเลือกเช่าหอพักระหว่างหอพัก A กับหอพัก B สมมติว่าเราต้องการความสะดวกสบาย (ระยะเวลาเดินทางไปที่ทำงานสั้น) และค่าเช่าไม่แพง เราจะเลือกหอพักใด หากทราบว่าเวลาที่ใช้ในการเดินทางไปที่ทำงานจากหอพัก A และ หอพัก B เป็น 30 และ 120 นาที ส่วนค่าเช่ารายเดือนของหอพัก A และหอพัก B เป็น 10,000 บาท และ 7,000 บาท ตามลำดับ

            จากข้อมูลที่ให้มา จะเห็นได้ว่าหอพักยิ่งใกล้ที่ทำงาน (ความสะดวกสบายเพิ่มขึ้น) ค่าเซ่าจะมีราคาแพงตามไปด้วย ดังนั้น วัตถุประสงค์ทั้งสองจึงขัดแย้งกันถ้าเรามีตัวเลือกมากขึ้น เราควรรวมสองวัตถุประสงค์ไว้เป็นวัตถุประสงค์เดียว เพื่อหาหอพักที่ให้ค่าต่ำสุดของระยะเวลา + ค่าเช่า แต่สำหรับคน ๆ หนึ่ง เวลา 1 นาทีที่ลดลงจากการเดินทางอาจไม่สามารถแลกกับราคาค่าเช่า 1 บาท ที่ลดลงได้ในทางกลับกัน สำหรับอีกคนหนึ่งราคาค่าเข่าที่ลดลง 1 บาทก็อาจไม่เพียงพอกับเวลา 1 นาทีที่ลดลงได้ ดังนั้น เราจึงไม่สามารถรวมสองวัตถุประสงค์ด้วยการจับมาบวกเข้าด้วยกันได้

            อย่างไรก็ตาม เราสามารถกำหนดน้ำหนัก w (0<w<1) เพื่อแทนความสำคัญของเวลา และนำไปคูณเข้ากับตัวแปรเวลา และทำการคูณน้ำหนักที่เหลือคือ 1-w เข้ากับตัวแปรค่าเช่า จากนั้น เราหาหอพักที่ให้ค่าต่ำสุดของปัญหา

[(w x เวลา) + ((1 - w) x ค่าเช่า)]

            ยกตัวอย่างเช่น ถ้าเรากำหนด w = 0.1 หมายถึง เรายอมรับได้กับการใช้เวลาเดินทางนาน เพื่อให้ได้มาซึ่งค่าเช่าที่ถูกในทางกลับกันหากเรากำหนด พ = 0.9 จะหมายถึงเราให้ความสำคัญกับเวลาค่อนข้างมาก และในกรณีสุดโต่งหากเรากำหนดให้ w = 1 คือค่าเข่าจะไม่มีผลต่อการตัดสินใจของเราแต่อย่างใด จะแพงเพียงใดก็ได้ ขอเพียงแต่หอพักอยู่ใกล้ที่ทำงานให้มากที่สุดเป็นพอ (เนื่องจากตัวคูณด้านหน้าของค่าเช่าเท่ากับ 0)

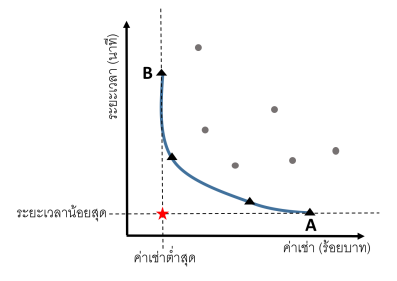
ภาพที่ 1 ให้แต่ละจุดสามเหลี่ยมและวงกลมแทนหอพัก (ทั้งหมด 10 จุด) โดยที่  แกน x แทนคำเช่าแกน y แทนเวลาเดินทางจากหอพักไปที่ทำงานเส้นโค้งทึบคือ Pareto Optimal Solution

            ตัวอย่างความสัมพันธ์ระหว่างค่าเช่า (ร้อยบาท) กับระยะเวลา (นาที) สามารถแสดงได้ดังภาพที่ 1 โดยหอพัก A เป็นจุดที่ใช้ระยะเวลาน้อยสุด และหอพัก B เป็นจุดที่มีค่าเช่าต่ำสุด เส้นประแสดงถึงค่เช่าต่ำสุดและระยะเวลาสั้นสุดที่เป็นไปได้เมื่อพิจารณาสองวัตถุประสงค์แยกกัน จุดดาวเป็นจุดที่เส้นประสองเส้นตัดกัน จึงเป็นจุดที่ให้ค่าเช่าต่ำสุดและระยะเวลาน้อยสุดสังเกตว่าไม่มีหอพักใดสอดคล้องกับจุดดาวซึ่งให้ค่าต่ำสุดของทั้งสองวัตถุประสงค์พร้อมกัน เส้นโค้งทึบแสดงตัวอย่างความเป็นไปได้ของกลุ่มคำตอบที่หมาะสมแบบพาเรโต เมื่อน้ำหนักแปรค่ในช่วง 0 ถึง 1 (0<w<1) จุดอื่น ๆ ที่ไม่ได้อยู่บนเส้นทึบนี้จะไม่มีทางเป็นคำตอบที่เหมาะสมของปัญหานี้ได้

            ดังนั้น คำตอบของปัญหาการเลือกเช่าหอพักจึงประกอบไปด้วยทุก 1 จุดบนเส้นทึบนี้ ซึ่งเรียกว่า เซตของผลเฉลยที่ไม่ถูกครอบงำ (Pareto Optimal Set) เป็นคำตอบที่ไม่มีคำตอบใดดีกว่า เป็นกลุ่มคำตอบที่เหมาะสมแบบพาเรโต (Pareto Optimal Solution โดยจุดเหล่านี้สามรถเป็นจุดที่ดีที่สุดได้ ทั้งนี้ขึ้นอยู่กับผู้ตัดสินใจว่าจะให้ความสำคัญกับวัตถุประสงค์ใดมากกว่ากัน สังเกตว่า กลุ่มคำตอบที่เหมาะสม เป็นสภาพที่เราไม่สามารถปรับเปลี่ยนเพื่อที่จะทำให้วัตถุประสงค์ใดวัตถุประสงค์หนึ่งดีขึ้น โดยไม่ทำให้วัตถุประสงค์อื่นแย่ลงได้ ยกตัวอย่างเช่น การจะให้ได้มาซึ่งค่าเช่าที่ลดลงของจุดบนเส้นโค้งทึบ (ไปทางซ้าย) จะต้องแลกด้วยระยะเวลาที่เพิ่มขึ้น (ขึ้นข้างบน) ตามภาพที่ 1

            มาถึงจุดนี้ ผู้อ่านอาจจะคิดถึงปัจจัยอื่นที่มีผลต่อการเลือกเข่าหอพัก เช่น ขนาดของห้องเช่า (ยิ่งใหญ่ยิ่งตี) ระยะทางจากหอพักไปยังห้างสรรพสินค้าที่อยู่ใกล้ที่สุด (ยิ่งใกล้ยิ่งดี) สำหรับคน ๆ หนึ่งปัจจัยเหล่านี้ อาจจะมีผลหรือไม่มีผลต่อการตัดสินใจ หากเรามีวัตถุประสงค์เท่ากับ 3 วัตถุประสงค์แล้ว เราสามารถที่จะแสดงกราฟพาเรโตเป็นภาพสามมิติ โดยให้แต่ละแกน (X. Y. Z) แทนแต่ละวัตถุประสงค์ แต่หากมีจำนวนมากกว่า 3 วัตถุประสงค์แล้ว เราจะไม่สามารถแสดงกราฟดังกล่าวได้ ในทางปฏิบัติการแก้ปัญหาค่าเหมาะสมที่มีวัตถุประสงค์จำนวนมากประกอบกับลักษณะฟังก์ซันวัตถุประสงค์ที่เป็นฟังก์ชันต่อเนื่อง (เช่น เวลา ระยะทาง) ทำให้ปัญหาดังกล่าวมีความซับซ้อนมาก (ผู้สนใจสามารถค้นคว้าวิธีการแก้ปัญหาดังกล่าวเพิ่มเติมได้จาก Deb. Kalyanmoy.Multi-objective optimization using evolutionary algorithms. Vol. 16. John Wiley & Sons, 2001. และ Zitzler, Eckart, Marco Laumanns, & Stefan Bleuler. (2004). A tutorial on evolutionary multiobjective optimization. Metaheuristics for multiobjective optimization, 3-37.)

            หลักการความเหมาะสมแบบพาเรโตนี้ถือกำเนิดจาก Vifredo Pareto (1848 - 1923) ซึ่งเป็นนักเศรษฐศาสตร์และสังคมศาสตร์ชาวอิตาลี ผู้ซึ่งโด่งดังจากการใช้คณิตศาสตร์ในการวิเคราะห์ปัญหาทางเศรษฐศาสตร์ โดยหลักการดังกล่าวถูกนำไปใช้ในการแก้ปัญหาทางทฤษฎีเกม การตัดสินใจ วิศวกรรมศาสตร์และปัญหาทางสังคมศาสตร์อีกมากมาย

บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Deb, Kalyanmoy. Multi-objective optimization using evolutionary algorithms Vol. 16. John Wiley & Sons, 2001.

Viltfredo Pareto. (1848-1923 ). Retrieved August 15, 2017, from http://www.econlib.org/ibrary/Enc/bios/Pareto.html.

Zitzler, Eckart Laumanns, Marco & Bleuler, Stefan. (2004). A tutorial on evolutionary multiobjective optimization. Metaheuristics for multiobjective optimization.

google map. สืบคั้นเมื่อ 15 สิงหาคม 2560, จาก https:/www.google.co.th/maps/dir/The+Grand+Palace,+Na+

Phra+Lan+Rd.+Phra+Nakhon.+ Bangkok.+10200/คณะวิทยาศาสตร์+มหาวิทยาลัยมหิดล.