เมื่อมีการกล่าวถึงคำว่า "ความชัน" เรามักมีจินตนาการถึงพื้นที่ที่มีความสูงเพิ่มมากตามระยะทางแนวราบที่เปลี่ยนไปเพียงเล็กน้อย เช่น ในกรณีของภูเขา และถนน หรือการหาความซันของกราฟที่มีความสัมพันธ์ระหว่างค่าในแกนนอนกับในแกนตั้ง

               ความรู้คณิตศาสตร์ของเรื่องนี้สามารถนำไปประยุกต์ใช้ในเรื่องอื่นได้ในลักษณะเดียวกัน แต่อาจใช้เรียกแตกต่างไป อย่างไรก็ตามในทางคณิตศาสตร์หมายถึงความลาดเอียง หรือศัพท์บัญญัติคณิตศาสตร์เรียก ความชัน

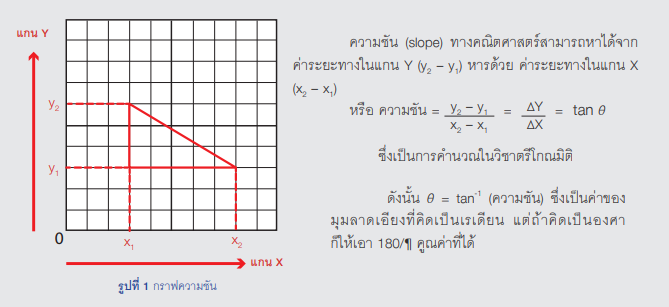
การนำความรู้คณิตศาสตร์มาใช้งานในวิทยาศาสตร์บางครั้งอาจมีคำเรียกอื่น แต่ถ้าพิจารณาวิธีหาค่าเหล่านั้นจะเห็นได้ว่าล้วนมาจากพื้นฐานคณิตศาสตร์เดียวกัน ดังตัวอย่างที่นำเสนอต่อไปนี้

ถ้าต้องเดินทางไปตามพื้นที่ที่มีความลาดชัน การขับรถจำเป็นต้องใช้ความระมัดระวังโดยเฉพาะการอ่านป้ายบอกสภาพทาง ที่จำเป็นต้องรู้ในการขับรถยนต์ เช่น ป้ายจำกัดความเร็ว และป้ายจราจร ซึ่งหากต้องขับรถในเส้นทางที่ลาดซันมากจำเป็นต้องสังเกตป้ายจราจร และควรขับรถตามคำแนะนำของป้ายเหล่านั้น เช่น ทางโค้ง ทางชัน ซึ่งการบอกความขันมักจะแสดงเป็นเปอร์เซ็นต์แล้วค่าที่คิดเป็นเปอร์เซ็นต์คือความขันหรือไม่

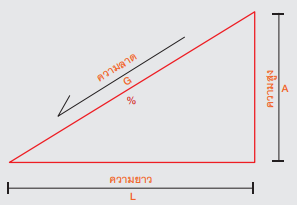
ในการบอกความลาดมักใช้อัตราส่วนระหว่าง D คือระยะทางตามความสูงของเส้นระดับ (vertical height) กับ Lคือ ระยะห่างระหว่างเส้นระดับในผัง (horizontal length) และ G คือความลาด (gradient) ซึ่งคำนวณได้จาก G = (D/L) x 100 และมีหน่วยเป็นเปอร์เซ็นต์ (%)

รูปที่ 2 ป้ายจราจร ประเภทป้ายเตือนทางลาดชัน
ที่มา กรมการขนส่งทางบก

             การเห็นป้าย "ทางขึ้นลาดซัน" (steep climb) แสดงว่าทางข้างหน้ามีความลาดชันขึ้น จึงอาจเป็นทางขึ้นเขา ขึ้นเนิน เป็นสันเขา หรือสันเนินโดยมีความลาดชันตามตัวเลขที่กำหนดเป็น "ร้อยละ" ตามที่ระบุในป้ายซึ่งอาจบดบังสายตาทำให้ไม่สามารถสังเกตเห็นรถที่สวนมาได้ ยกตัวอย่างเช่น ข้างหน้าเป็นทางลาดขันขึ้นเขา และมีเลข 8% กำกับไว้ หมายถึง ระยะทางของเนินนี้หากมีความยาวในแนวราบเท่ากับ 100 เมตรจุดหมายปลายทางของการเดินทางจะอยู่สูงกว่าความสูงเดิม 8 เมตร (หรือเท่ากับ 8 หาร 100 คูณ 100 เท่ากับ 8%) ในทางตรงกันข้ามถ้าเป็นกรณีทางลงเขา และปรากฏเลข 8% ก็ให้คิดในลักษณะเดียวกัน เพียงเปลี่ยนจากระดับความสูงที่เพิ่มขึ้น เป็นระดับความสูงที่ลดลงจากเดิมหากเป็นทางลาดซันมีเลขกำกับคือ 10% และ 15% ทางนั้นก็จะมีความชันที่มากขึ้น กรณีสะพานพระราม 9 มีเลขกำกับคือ 5% แสดงว่า เมื่อระยะทางในแนวราบเปลี่ยนไป 1 เมตร ระยะทางในแนวดิ่งจะเปลี่ยนแปลง 5 เซนติเมตร (เนื่องจากสะพานนี้มีทั้งการเพิ่มและและลดลงของความชัน)

            การแสดงค่าความชันในลักษณะสุดท้ายที่จะกล่าวต่อไปนี้เป็นค่าที่บอกความชันที่อาจจะยากต่อการเข้าใจของหลายคน เพราะไม่แสดงความชันให้เห็นโดยการสังเกตความชันดังกล่าวคือ "ความขันของความกดอากาศ" ซึ่งเป็นตัวแปรหนึ่งทางอุตุนิยมวิทยาที่สามารถวัดได้และใช้ในการวิเคราะห์เส้นความกดอากาศเท่า (isobar) ในแผนที่อากาศเพื่อแสดงความดันอากาศในแต่ละบริเวณ เช่น หย่อมความกดอากาศต่ำ (low pressure cell) บริเวณความกดอากาศสูง (high pressure area) รวมถึงพายุหมุนเขตร้อน และแนวปะทะอากาศ (front) ในประเทศไทยการวิเคราะห์เส้นความกดอากาศเท่าจะมีระยะห่างระหว่างเส้นเท่ากับ 2 hPa (hectopascal หน่วยของความกดอากาศ) ซึ่งบางครั้งเส้นอาจจะอยู่ใกล้กันมากโดยเฉพาะในฤดูหนาว ส่วนในฤดูร้อนเส้นความกดอากาศเท่าจะอยู่ห่างกันมาก

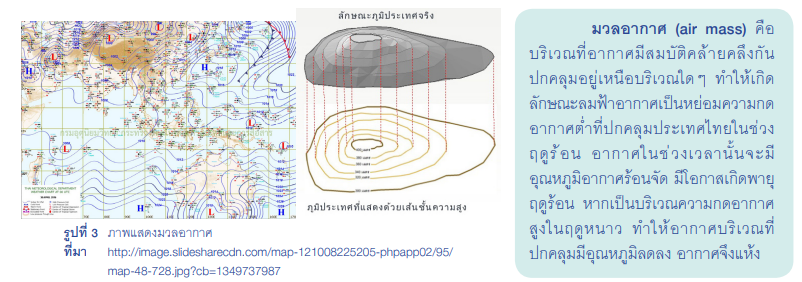
            ตัวอย่างแผนที่อากาศของวันที่ 17 กรกฎาคม พ.ศ. 2559 ขณะเวลา 07.00 น. (รูปที่ 3) แสดงเส้นความกดอากาศเท่าในแผนที่อากาศซึ่งมีลักษณะเป็นส้นโค้ง และในกรณีสมบัติของอากาศโดยทั่วไป อุณหภูมิจะมีความสัมพันธ์กับความกดอากาศ กล่าวคือ อากาศที่มีอุณหภูมิสูงจะขยายตัวทำให้ความหนาแน่นของอากาศลดลงจึงลอยตัวสูงขึ้น ส่งให้ความกดอากาศต่ำ ส่วนบริเวณที่มีอุณหภูมิต่ำอากาศจะจมลงสู่เบื้องล่าง ทำให้ความหนาแน่นของอากาศเพิ่มขึ้น ส่งผลให้เกิดความกดอากาศสูง หากพิจารณาเปรียบเทียบกับเส้นความสูงของภูเขา (รูปที่ 3) โดยความกดอากาศต่ำเปรียบเสมือนบริเวณที่มีระดับความสูงไม่มาก ดังนั้น ถ้าปล่อยวัตถุจากที่สูง วัตถุจะเคลื่อนที่ลงมายังพื้นที่ต่ำกว่า การเคลื่อนที่ของอากาศก็เป็นไปในลักษณะเดียวกัน คือ อากาศในบริเวณที่มีความกดอากาศสูงกว่า (มีความชันมากกว่า) จะเคลื่อนที่ไปยังบริเวณที่มีความกดอากาศต่ำกว่า (ความชันน้อยกว่า) เสมอ ความชันของความกดอากาศนี้ใช้หลักการคำนวณเดียวกันกับการหาความชันทางคณิตศาสตร์ดังที่กล่าวมาแล้ว โดยให้แกน Y เป็นความกดอากาศ และแกน X เป็นระยะทาง โดยอาศัยความรู้เรื่อง "อนุพันธ์ของฟังก์ชัน" ในวิชาแคลคูลัสเบื้องตัน (หนังสือรายวิชาเพิ่มเติม คณิตศาสตร์ เล่ม 6 มัธยมศึกษาปีที่ 4-6) ซึ่งแสดงการหาความชันของเส้นสัมผัสเส้นโค้งได้ ดังความสัมพันธ์ต่อไปนี้

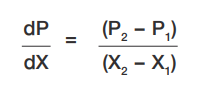
             เนื่องจากความแตกต่างของความกดอากาศตามระยะทางแสดงทิศการเคลื่อนที่ของอากาศ ดังนั้นความชันจึงเป็นปริมาณเวกเตอร์ หรือมีอีกชื่อหนึ่งว่า เกรเดียนท์ (gradient) และเรียกความชันที่เกิดจากความกดอากาศที่แตกต่างกันนี้ว่า ความชันของความกดอากาศ (pressure gradient) มักใช้สัญลักษณ์   ซึ่งถ้ากล่าวถึงการเคลื่อนที่เราย่อมหมายถึงว่ามีแรงมากระทำกับวัตถุ ในวิชาอุตุนิยมวิทยาก็เช่นกัน แรงที่ส่งผลต่อการเคลื่อนก็คือแรงที่เกิดจากความชันของความกดอากาศ (pressure gradient force) ซึ่งแสดงได้ดังความสัมพันธ์

             บริเวณใดที่มีความแตกต่างของความกดอากาศมากจะสังเกตเห็นได้จากเส้นความกดอากาศเท่าที่อยู่ไกลกันมากจะมีอัตราเร็วลมมากกว่าบริเวณที่มีความแตกต่างของความกดอากาศน้อยกว่า ดังนั้นในฤดูหนาวลมจะพัดแรงกว่าในฤดูร้อน (ยกเว้นในช่วงเวลาที่เกิดฝนฟ้าคะนองซึ่งจะมีลมพัดในบริเวณนั้นรุนแรงกว่าปกติ

            แม้ความชันของความกดอากาศจะไม่สามารถวัดความชันจริงโดยใช้เครื่องมือเหมือนการวัดความชันของภูเขา อย่างไรก็ตามการประยุกต์ใช้ความรู้ทางคณิตศาสตร์เพื่อหาความสัมพันธ์ในทางวิทยาศาสตร์ วิศวกรรม หรือศาสตร์อื่น ๆ บางครั้งอาจมีชื่อเรียกที่แตกต่างกัน แต่การแปลความหมายหรือการนำไปใช้ล้วนเป็นเรื่องเดียวกัน

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

ป้ายจราจร ประเภทป้ายเดือน. สืบคั้นเมื่อ 9 กันยายน 2559, จาก https:/www.dlt go.th/.

แผนที่อากาศ. สืบคั้นเมื่อ 9 กันยายน 2559, จาก http:/www.tmd.go.th/weather_map.php.

มวลอากาศ. สืบคั้นเมื่อ 9 กันยายน 2559, จาก  http://image.slidesharecdn.com/map-121008225205-phpapp02/95/map-48-728.jpg?cb=1349737987