หลายท่านที่อ่านชื่อเรื่องของบทความนี้แล้วอาจสงสัยว่าคณิตศาสตร์เกี่ยวข้องกับศพอย่างไรในบทความนี้จะเสนอความรู้ทางคณิตศาสตร์ที่ใช้ในการสืบจากศพ นั่นคือ ฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการทึม

            ฟังก์ชันเอกซ์โพเนนเชียลเป็นฟังก์ชันที่มีความสำคัญในการศึกษาความรู้ในด้านต่าง ๆ เช่น อัตราการเพิ่มจำนวนของแบคที่เรีย อัตราการสลายตัวของยาในร่างกายของมนุษย์ การหายอดเงินฝากธนาคาร ส่วนฟังก์ชันลอการิทึมจะพบในการศึกษาวิทยาศาสตร์ในด้านต่าง ๆ เช่น ค่า pH  ระดับความเข้มเสียง โดยในบทความนี้จะกล่าวถึงการนำความรู้เกี่ยวกับฟังก์ชันเอกซ์โพเนนเชียลและฟังก์ชันลอการิทึมไปประยุกต์ใช้กับการหาระยะเวลาหลังการตาย

            ในปัจจุบันวิธีทางการแพทย์ต่าง ๆ ยังไม่สามารถตรวจหาระยะเวลาหลังการตายที่แน่นอนได้ โดยการเปลี่ยนแปลงของร่างกายหลังการตายจะขึ้นกับสภาพสิ่งแวดล้อมและเวลาหลังการตาย ถ้าสภาพสิ่งแวดล้อมแตกต่างกัน การเปลี่ยนแปลงของร่างกายก็จะแตกต่างกันและถ้าตายมานานมากจะทำให้การหาระยะเวลาการตายมีความคลาดเคลื่อนมากด้วย

            การเปลี่ยนแปลงอุณหภูมิร่างกายของผู้ตายที่เกิดขึ้นหลังการตาย (post-mortem body cooling) สามารถนำไปใช้ทำนายระยะเวลาหลังการตายอย่างคร่าว ๆ โดยการเขียนฟังก์ชันของอุณหภูมิเทียบกับเวลาเมื่อกำหนดค่าคงตัว Z ดังนี้

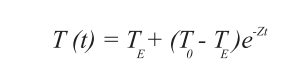
            โดย T₀ แทนอุณหภูมิร่างกายของคนทั่วไป T_E แทนอุณหภูมิสิ่งแวดล้อม Z แทนค่าคงตัวในที่นี้จะกำหนดให้ T₀ แทนอุณหภูมิศีรษะของคนทั่วไป ซึ่งจะประมาณ 33 ^๐C และจากงานวิจัยกำหนดให้ Z เป็น 0.1 มีหน่วยเป็น 1/ชั่วโมง ถ้าอุณหภูมิสิ่งแวดล้อม T_E เป็น 15 ^๐C จะเขียนกราฟแสดงความสัมพันธ์ระหว่างอุณหภูมิศีรษะของผู้ตายและระยะเวลาหลังการตาย ได้ดังนี้

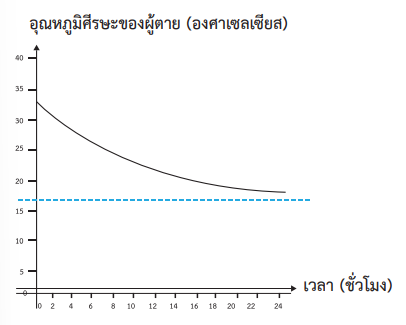
            จากกราฟจะเห็นว่าเมื่อเวลาผ่านไป อุณหภูมิศีรษะของผู้ตายก็จะลดลงจนเข้าใกล้อุณหภูมิสิ่งแวดล้อม

            การหาระยะเวลาหลังการตายข้างต้นเป็นเพียงการประเมินอย่างง่ายเท่านั้น เพราะยังไม่ได้คิดเงื่อนไขอื่น ๆ เช่น เสื้อผ้าท่าของผู้ตาย บริเวณที่ตาย ซึ่งเป็นปัจจัยที่มีผลต่อการลดลงของอุณหภูมิด้วย ดังนั้น ถ้าจะหาเวลาการตายที่มีความคลาดเคลื่อนน้อย จะต้องใช้ความรู้เกี่ยวกับการเปลี่ยนแปลงหลังการตายอื่น ๆ มาประกอบกัน ได้แก่ การตกของเลือดตามแรงโน้มถ่วงการแข็งตัวของกล้ามเนื้อ อัตราการเน่า การเปลี่ยนแปลงทางเคมีในร่างกาย ปริมาณอาหารในกระเพาะ การเจริญเติบโตของตัวหนอน และวัตถุพยานในที่เกิดเหตุ

            จากตัวอย่างที่กล่าวมาคงจะตอบข้อสงสัยของทุกท่านแล้วนะคะว่าคณิตศาสตร์กับศพเกี่ยวข้องกันได้อย่างไร นอกจากนี้คณิตศาสตร์ยังเกี่ยวข้องกับชีวิตของเราอีกมากมาย ไว้ติดตามในโอกาสต่อไปค่ะ

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Adam, Craig. (2010). Essential Mathematics and Statistics for Forensic Science. UK: Wiley -Blacwell. ระยะเวลาการตายและการเปลี่ยนแปลงหลังตาย. สืบค้นเมื่อ 1 พฤศจิกายน 2556, จาก http://www.ifrm.go.th/ifm-book/ifm-textbook/114-lesson3.html.