ในการศึกษาของประเทศไทย ได้จัดให้มีการศึกษาเรื่องตัวแบบเชิงคณิตศาสตร์ (Mathematical Model) ในระดับชั้นปริญญาตรี ทั้งในสาขาคณิตศาสตร์ สถิติวิทยาการคอมพิวเตอร์ คณิตศาสตร์ประยุกต์ การบัญชีการจัดการ และเศรษฐศาสตร์ เพื่อให้ผู้เรี่ยนมีความรู้ในระดับสูงเพียงพอที่จะนำไปใช้เป็นความรู้พื้นฐานในการสร้างตัวแบบเชิงคณิตศาสตร์ ในปีค.ศ. 2001 Ang Keng Cheng นักวิจัยจาก National Institute of Education  จากประเทศสิงคโปร์  ได้เสนอการจัดการเรียนการสอนเรื่องตัวแบบเชิงคณิตศาสตร์ในระดับชั้นมัธยมศึกษาผ่านงานวิจัยเรื่อง Teaching Mathematical Modelling in Singapore Schools โดยยกตัวอย่างการจัดการเรียนการสอนที่แนะนำให้ผู้เรียนรู้จักตัวแบบเชิงคณิตศาสตร์ผ่านปัญหาในชีวิตจริง ซึ่งแปลงปัญหาดังกล่าวโดยใช้หลักการสร้างตัวแบบเชิงคณิตศาสตร์ และนำความรู้ทางคณิตศาสตร์ช่วยในการหาคำตอบ เช่นการสร้างลานจอดรถที่มีอยู่อย่างจำกัดโดยการใช้ความรู้เรื่องตรีโกณมิติ การสร้างกล่องที่มีความจุมากที่สุดโดยใช้ความรู้เกี่ยวกับอนุพันธ์การศึกษาเกี่ยวกับอัตราการเพิ่มของประชากรโดยใช้ความรู้เรื่องฟังก์ชันเลขชี้กำลัง

            การเริ่มต้นให้ผู้เรียนรู้จักตัวแบบเชิงคณิตศาสตร์ในระดับชั้นมัธยมศึกษานั้น เริ่มด้วยการยกตัวอย่างปัญหาในชีวิตจริงมาอธิบายขั้นตอนของการสร้างตัวแบบเชิงคณิตศาสตร์ จะสามารถแนะนำให้ผู้เรียนรู้จักตัวแบบเชิงคณิตศาสตร์และอธิบายขั้นตอนในการสร้างได้ไม่ยากเพราะเป็นการอาศัยความคุ้นเคย  และใช้ความรู้พื้นฐานที่ผู้เรียนมีอยู่แล้วมาช่วยในการหาคำตอบของปัญหา ดังเช่น ตัวอย่างปัญหาต่อไปนี้

            จะเห็นได้ว่าปัญหาขายบัตรงานคืนสู่เหย้าให้ได้กำไรมากที่สุดนี้ แตกต่างจากปัญหาทางคณิตศาสตร์ทั่วไปเนื่องจากเป็นปัญหาปลายเปิดที่ไม่มีการระบุค่าของตัวแปรใด ๆ  มาให้ ซึ่งผู้แก้ปัญหาจะต้องคาดการณ์หรือระบุตัวแปรที่เกี่ยวข้องกับการหากำไรของการขายบัตร เช่น จำนวนบัตรหรือมูลค่าของรางวัลด้วยตนเอง จะเห็นว่านี่คือ "ความแตกต่างระหว่างโจทย์ปัญหาคณิตศาสตร์ทั่วไปและตัวแบบเชิงคณิตศาสตร์" จากนั้นนำความรู้พื้นฐานและเทคนิคการแก้ปัญหาทางคณิตศาสตร์มาใช้กับปัญหา วิธีการดังกล่าวนี้เรียกว่า "การสร้างตัวแบบเชิงคณิตศาสตร์"

            จากปัญหางานคืนสู่เหย้า แปลงปัญหาดังกล่าวโดยใช้หลักการสร้างตัวแบบเชิงคณิตศาสตร์ และนำความรู้ทางคณิตศาสตร์ช่วยในการหาคำตอบ ตามขั้นตอนต่อไปนี้

1. ระบุคำถามที่เกี่ยวข้องกับปัญหางานคืนสู่เหย้า เช่น บัตร์คืนสู่เหย้ามีราคาเท่าใดบ้างบัตรคืนสู้เหย้าแต่ละใบมีราคาเท่ากันหรือไม่มูลค่าของรางวัลเป็นเท่าใดบ้างมี้ค่าใช้จ่ายในการดำเนินการอื่น ๆ เพิ่มเติมหรือไม่
2. ระบุและบอกชนิดของตัวแปรที่เกี่ยวข้องกับปัญหา เช่นราคาบัตร จำนวนบัตรที่ขายได้ มูลค่าของรางวัลและค่าใช้จ่ายในการดำเนินการ โดยแจกแจงรายละเอียดของตัวแปรต่าง ๆ ดังแสดงในตาราง

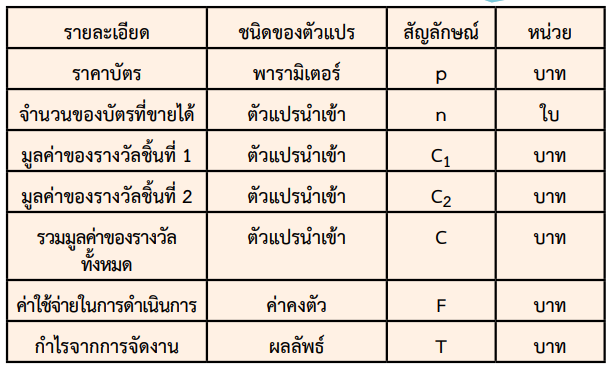
            จากตารางข้างต้น  ชนิดของตัวแปรพารามิเตอร์คือตัวแปรที่ผู้แก้ปัญหากำหนดให้คงที่สำหรับแต่ละตัวแบบซึ่งสามารถเปลี่ยนแปลงค่าได้ เมื่อสมมติฐานเปลี่ยนแปลงไป

3. ตั้งสมมติฐานเพื่อแก้ปัญหาที่กำหนด สมมติฐานหนึ่งที่เป็นไปได้คือ กำหนดให้บัตรทุกใบมีราคาเท่ากัน
4. สร้างข้อความทางคณิตศาสตร์จากสมมติฐานที่ตั้งไว้โดยใช้สัญลักษณ์ของตัวแปรที่กำหนดไว้ในตารางข้างต้นและอาจใช้คำถามนำดังนี้

5. แปลความหมายและตรวจสอบว่าคำตอบที่ได้นั้นทำให้ตัวแบบเชิงคณิตศาสตร์ที่สร้างสอดคล้องกับความเป็นจริงหรือไม่ เช่น จำนวนของบัตรควรเป็นจำนวนเต็มบวก ทั้งนี้อาจเปลี่ยนแปลงสมมติฐานของตัวแบบ เช่น ถ้าราคาบัตรเพิ่มขึ้นหรือบัตรมีราคาไม่เท่ากัน จะเกิดการเปลี่ยนแปลงหรือต้องปรับเปลี่ยนตัวแบบอย่างไรบ้าง

            จากขั้นตอน 1-5 ของการสร้างตัวแบบเชิงคณิตศาสตร์จากปัญหางานคืนสู่เหย้านั้น จะเห็นได้ว่าเป็นการเปลี่ยนปัญหาในโลกของชีวิตจริงไปสู่โลกที่ไม่มีตัวตนนั่นคือ โลกของตัวแบบเชิงคณิตศาสตร์ซึ่งสร้างขึ้นโดยอาศัยแนวคิดทางคณิตศาสตร์ เช่น ฟังก็ชันและสมการจากนั้นอาศัยเทคนิคทางคณิตศาสตร์ช่วยในการคำนวณเพื่อหาผลเฉลยของปัญหาทางคณิตศาสตร์  ท้ายที่สุดแล้วผู้แก้ปัญหาต้องแปลงผลเฉลยกลับสู่โลกของชีวิตจริง ซึ่งจะเห็นว่าจุดเริ่มต้นและจุดสุดท้ายของการสร้างตัวแบบเชิงคณิตศาสตร์คือ โลกของชีวิตจริง

            ในการสร้างตัวแบบเชิงคณิตศาสตร์ที่ใกล้เคียงและสอดคล้องกับปัญหานั้น ผู้สร้างตัวแบบจะต้องเข้าใจสถานการณ์ที่ต้องการแก้ปัญหาอย่างถ่องแท้และเริ่มต้นอย่างถูกทิศทางจะช่วยให้ผู้สร้างตัวแบบสามารถนำวิธีการทางคณิตศาสตร์มาใช้ในการแก้ปัญหาได้ใกล้เคียงกับความเป็นจริงมากที่สุด

             บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/   

บรรณานุกรม

Ang Keng Cheng. (2001). Teaching Mathematical Modelling in Singapore Schools. The Mathematics Educators. 6, 1. 63-75.

ธีรวัฒน์ นาคะบุตร. (2546). ตัวแบบเชิงคณิตศาสตร์ (Mathematical Modeling) นครปฐม: คณะวิทยาศาสตร์ และเทคโนโลยี สถาบันราชภัฏนครปฐม.