การท่องสูตรคูณมักเป็นประเด็นปัญหาให้ถกเถียงกันบ่อยครั้งว่า การสอนเรื่องคูณ ควรให้ท่องสูตรคูณหรือไม่ ในบทความนี้จึงขอเสนอวิธีสอน เรื่อง การคูณ จำนวนนับแบบหนึ่ง ให้ช่วยกันพิจารณาว่า ...ท่องหรือไม่ท่อง...

   หลังจากสร้างข้อตกลง เรื่อง การคูณ โดยตกลงกันว่า กรณีที่มีการบวกจำนวนนับจำนวนเดียวกันหลายตัว เช่น 2 + 2 + 2 + 2 จะใช้วิธีการเขียนแบบใหม่ โดยให้นับจำนวนที่บวกกันว่ามีกี่จำนวน ในที่นี้มี 2 บวกกันทั้งหมดสี่จำนวน จึงเขียนใหม่ว่า 4 × 2 แปลว่า มี 2 บวกกัน 4 ตัว เมื่อหาผลบวกได้ 8 จะเรียกว่า 4 × 2 ได้ผลคูณ 8 นั่นคือ

4 × 2 = 8

   ในทำนองเดียวกัน จะได้ว่า 6 × 2 = 12 และ 7 × 5 = 35

   เมื่อซักซ้อมความเข้าใจจนแน่ใจแล้วว่า การหาผลคูณของจำนวนนับ เช่น 5 × 7 นักเรียนจะนำ 7 ห้าตัวมาบวกกันและใช้ผลบวกเป็นคำตอบ จะได้ว่า

5 × 7 = 35

   ครูให้นักเรียนสร้างตารางขนาด 10 × 10 ซม. บนกระดาษที่เตรียมไว้ แล้วเขียนเครื่องหมายคูณและจำนวนนับ 1 ถึง 9 ดังนี้

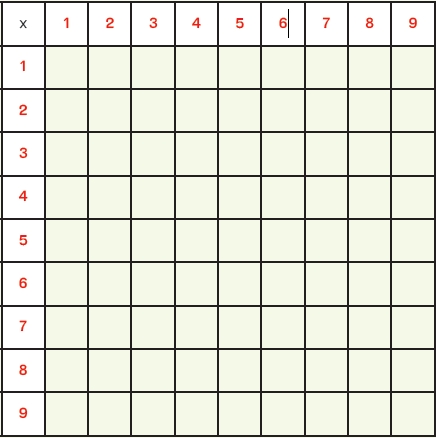
ตารางแสดงผลคูณขนาด 10 × 10 ซม.

   ครูบอกนักเรียนว่า ให้ช่วยกันสร้างตารางแสดงผลคูณของจำนวนนับตั้งแต่ 1 ถึง 9 เพื่อใช้ช่วยในการหาผลคูณ จากนั้นนักเรียนและครูช่วยกันคิดหาผลคูณในคอลัมน์แรก นั่นคือ ผลคูณของ 1 × 1, 2 × 1, 8 × 1, 9 × 1 ในคอลัมน์แรกจะเป็นดังนี้

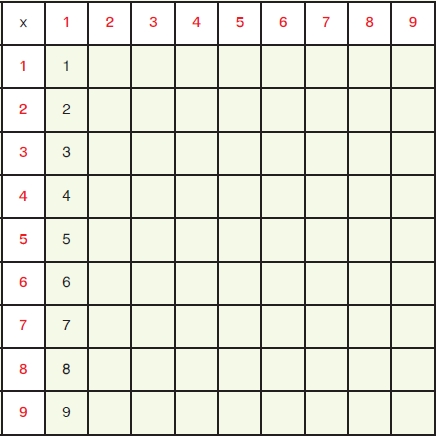
ตารางแสดงผลคูณขนาด 10 × 10 ซม.

   ครูบอกให้นักเรียนทราบว่า นี่คือสูตรคูณแม่ 1 และให้ท่องว่า หนึ่ง หนึ่ง ได้หนึ่ง หนึ่ง สอง ได้สอง โดยขณะที่ท่องก็ชี้ตำแหน่งของจำนวนนับและตามด้วยการออกเสียง เช่น ออกเสียงว่า หนึ่ง ห้า ได้ ห้า ก็ชี้ที่ตัวเลขหนึ่งที่อยู่หัวคอลัมน์ เลขห้าที่ช่องซ้ายมือสุด และตามด้วยเลขห้าที่ช่องที่สองตามลำดับ เมื่อนักเรียนเข้าใจดีแล้ว ครูบอกให้นักเรียนสร้างสูตรคูณแม่ 2 ด้วยตนเอง เมื่อทำเสร็จแล้วตรวจสอบว่า ผลคูณที่หาได้ของตนเองถูกต้องตรงกันกับของเพื่อนหรือไม่ ทำเช่นนี้จนได้ตารางแสดงผลคูณที่ถูกต้องสมบูรณ์ ดังนี้

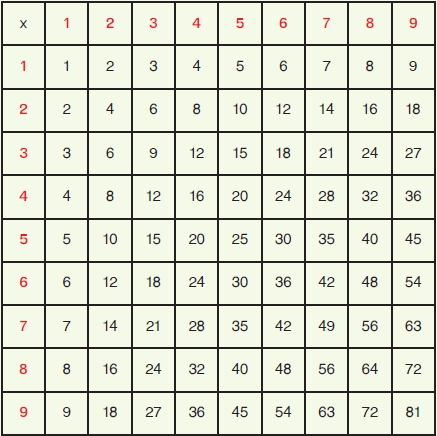
ตารางแสดงผลคูณ ขนาด 10 × 10 ซม.

หมายเหตุ

   1. ครูต้องให้นักเรียนสร้างตารางด้วยตนเอง จะได้เข้าใจวิธีหาผลคูณโดยใช้การบวกต่อเนื่อง

   2. ขณะที่นักเรียนกำลังสร้างตาราง ครูควรสังเกตทักษะการบวก ทักษะในการทำงานของนักเรียน

   3. หาวิธีตรวจสอบตารางของทุกคนให้ถูกต้อง เพราะต้องใช้ประกอบการเรียนต่อไป

   ในช่วงที่นักเรียนยังจำสูตรคูณไม่ได้และต้องมีการหาผลคูณ ครูควรให้นักเรียนใช้ตารางแสดงผลคูณในการตรวจสอบผลคูณ และใช้เป็นอุปกรณ์ประกอบการอภิปรายประเด็นต่าง ๆ โดยให้ตอบคำถามต่อไปนี้

   1. ตารางแสดงผลคูณที่สร้างขึ้น แสดงผลคูณของจำนวนทั้งหมดกี่คู่ อธิบายวิธีหาคำตอบ

   แนวตอบ แสดงผลคูณของจำนวนนับ 9 × 9 หรือ 81 คู่ โดยพิจารณาจากแต่ละแถวแสดงผลคูณของจำนวนนับ 9 คู่ เมื่อมีจำนวนแถวทั้งหมด 9 แถว จำนวนคู่จึงเป็นผลบวกของ 9 เก้าตัว  ซึ่งก็คือ 9 × 9 และจากตารางแสดงผลคูณจะได้ 81 เป็นผลคูณ

   2. จากคำตอบของข้อ 1 จงหาว่ามีกี่คู่ที่ผลคูณเท่ากัน แต่ละคู่มีลักษณะอย่างไร

   แนวตอบ มีทั้งหมด 1 + 2 ... ... + 7 + 8 หรือ 4 × 9 หรือ 36 คู่ ทุกคู่เหมือนกันในลักษณะ a × b และ b × a เมื่อ a, b เป็นจำนวนนับ 1 ถึง 9 ครูควรบอกเรื่อง สมบัติการสลับที่ของการคูณจำนวนนับ และเมื่อถึงตรงนี้ 3 × 2 = 2 × 3 การหา 3 × 2 อาจใช้ 3 + 3 ก็ได้แล้ว แสดงว่าไม่ว่า 2 คูณจำนวนใดก็ใช้จำนวนนั้นมาบวกกัน เช่น 7 × 2 = 7 + 7 = 14 เมื่อเป็นเช่นนี้สูตรคูณแม่ 2 ก็ไม่ต้องท่อง เพราะใช้การบวกแทนได้

   3. จากข้อ 2 และการที่สามารถหาผลคูณของจำนวนด้วย 2 ได้ จงพิจารณาว่าสามารถนำไปใช้ในการหาผลคูณของจำนวนนับใด

   แนวตอบ ใช้ในการหาผลคูณของจำนวนนับใดๆ ด้วย 4 และ 8 เพราะ 4 = 2 × 2 , 8 = 2 × 2 × 2 ดังนั้น ผลคูณของจำนวนนับด้วย 4 และ 8 หาได้ดังนี้

   7 × 4 → 7 × 2 × 2 →14 × 2 → 28

   9 × 8 → 9 × 2 × 2×2 → 18 × 2 × 2 →  36 × 2 → 72

   4. ถ้าเพิ่มเติมสมบัติการแจกแจงที่บอกให้ทราบว่า การคูณจำนวนนับกับจำนวนที่เขียนในรูปการบวกผลคูณ เมื่อหาผลบวกก่อนจะเท่ากับผลบวกของผลคูณของจำนวนที่นำมาคูณ คูณกับแต่ละจำนวนที่บวกกัน นั่นคือ

   a × (b + c) = (a × b) + (a × c) เมื่อ 2, 6, c คือ จำนวนนับ

   ถ้าใช้ความรู้นี้ประกอบกับการหาผลคูณเมื่อคูณด้วย 2 จะทำให้หาผลคูณเมื่อคูณด้วยจำนวนนับอื่นนอกจาก 4 กับ 8 ได้อีกหรือไม่

   แนวตอบ ได้ทั้งการคูณ เช่น  3, 5, 6, 7 และ 9 เพราะ 3 = 2 + 1 , 5 = 4 + 1 , 6 = 4 + 2 , 7 = 4 + 3 , 9 = 4 + 4 + 1 เช่น

   9 × 7 = (9 × 4) + (9 × 3)

            = (9 × 4) + (9 × 2) + (9 × 1)

            = 36 + 18 + 9

            = 63

   ทั้งหมดเป็นการนำเสนออย่างคร่าว ๆ ว่า จะท่องสูตรคูณหรือไม่ท่องก็ได้แล้วแต่จะเลือก ถ้ายึดหลักสายกลาง ผู้เขียนเห็นว่า สูตรคูณที่ไม่ต้องท่องคือ

   สูตรคูณแม่ 2 และ 3 เพราะใช้การบวกต่อเนื่องช่วยได้

   สูตรคูณแม่ 5 ท่องจำได้ง่าย ที่เหลือใช้วิธีตามที่นำเสนอมา เช่น ต้องการหา 9 × 9 จะได้ว่า

   9 × 9 = (9 × 5) + (9 × 4)

            = 45 + 36

   หรือ 9 × 9 = 45 + 9 + 9 + 9 + 9

   โดยสรุป การผสมผสานระหว่างการท่องสูตรคูณ และความสามารถในการนำสมบัติของจำนวนมาใช้ จะช่วยลดความผิดพลาดจากการจำผิดได้มาก ทั้งนี้ครูต้องตระหนักว่า ในชั้น ป.1 ถึง ป.3 ทักษะการบวกจำนวนนับ a + b เมื่อ a, b คือ จำนวนนับ 1 ถึง 9 และ 0 มีความสำคัญมาก ถ้านักเรียนยังหา 8 + 7 โดยการนับนิ้วอยู่ถือว่าใช้ไม่ได้ ควรคิดในใจได้ว่า 8 + 2 = 10 ,10 + 5 = 15 หรือจำได้ว่า คือ 15 การฝึกอภิปรายประเด็นที่ผู้เขียนเสนอเป็นเรื่องสำคัญ เพราะว่านักเรียนได้ใช้ความรู้ที่เรียนมาในการแก้ปัญหา เป็นการฝึกให้คิดหาวิธีที่แตกต่างจากเดิม ฝึกสมาธิ  ถ้าครูยึดหลักการสอนแบบให้คิดโดยใช้การถามนำให้คิด จะช่วยฝึกทักษะการคิดปรับปรุงงานให้ติดตัวนักเรียนไปตลอดชีวิต แต่การคิดจะเกิดสิ่งใหม่ ๆ ที่ดีขึ้นเสมอ ขอจบด้วยคำโบราณว่า "การคำนวณควรชำนาญ คูณหารเป็น" เทคนิคการคูณโดยใช้ 10 ช่วยเป็นประเด็นที่ฝากให้พิจารณากันต่อเอง เช่น 9 × 7 = 70 - 7 = 63, 5 × 9 = 90 ÷ 2 = 45  

ตัวเลข 0-9 , สัญลักษณ์การคูณ , เครื่องหมายเท่ากับ

บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ปีที่ 49 ฉบับที่ 228 มกราคม - กุมภาพันธ์ 2564

ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://emagazine.ipst.ac.th/

บรรณานุกรม

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). หนังสือเรียนรายวิชาพื้นฐานคณิตศาสตร์ ชั้นประถมศึกษาปีที่ 2 เล่ม 1 ตามมาตรฐานการเรียนรู้และตัวชี้วัดกลุ่มสาระการเรียนรู้คณิตศาสตร์ (ฉบับปรับปรุง พ.ศ. 2560) ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551. กรุงเทพมหานคร: โรงพิมพ์สกสค. ลาดพร้าว.