หอคอยฮานอย  (Tower of Hanoi)

อุปกรณ์

แผ่นไม้กลมเจาะช่องตรงจุดศูนย์กลางให้พอดีกับการสวมเข้าหลักที่ตอกติดบนแผ่นไม้ซึ่งเป็นฐาน มีหลัก  3  หลัก  จำนวน  5  ชิ้น  (อาจมีจำนวนมากหรือน้อยกว่านี้ก็ได้)    มีขนาดลดหลั่นกันเป็นลำดับทั้ง 5  ชิ้น  นำแผ่นไม้ทั้ง  5  ชิ้น  สวมเข้ากับหลักใดหลักหนึ่งเรียงลำดับตามขนาดให้แผ่นใหญ่อยู่ข้างล่าง  เพื่อให้ง่ายในการสื่อความหมาย  ขอแทนไม้แผ่นเล็กสุดที่อยู่ด้านบนสุดว่าแผ่นที่  1  แผ่นใหญ่ขึ้นถัดลงมาเป็นแผ่นที่  2  ,  3  , ...  และ  5  ตามลำดับ  ดังรูป

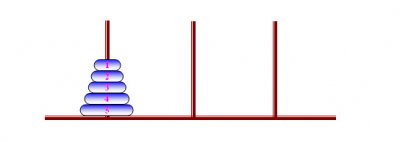
วิธีการเล่น

1. ให้ย้ายแผ่นไม้มีอยู่  5  แผ่น  ที่สวมไปไว้อีกหลักหนึ่งหลักใดก็ได้
2. การย้ายแผ่นไม้ทั้งหมดมีเงื่อนไขว่า

–  ต้องวางแผ่นไม้แผ่นเล็กไว้ด้านบนแผ่นใหญ่เสมอ

–  หยิบแผ่นไม้ในการย้ายได้ครั้งละ  1  แผ่น

1. ให้จำนวนครั้งในการย้ายแผ่นไม้น้อยที่สุด (การย้ายแต่ละครั้งหมายถึงการย้ายแผ่นไม้  1  แผ่น  จากหลักหนึ่งไปไว้ยังอีกหลักหนึ่ง)

สำหรับการเริ่มต้นการเล่น  นักเรียนอาจย้ายแผ่นไม้แบบลองผิดลองถูก  เพื่อแก้ปัญหาแต่สักระยะเวลาหนึ่ง  จะมองเห็นว่าน่าจะลดจำนวนแผ่นไม้ลงให้มีจำนวนน้อยแผ่นก่อน  ซึ่งง่ายต่อการแก้ปัญหา จากนั้นจึงเพิ่มจำนวนแผ่นไม้ให้มากขึ้น  โดยอาศัยแนวคิดที่ได้จากการแก้ปัญหาจำนวนแผ่นไม้ที่น้อย  แล้วนำไปใช้แก้ปัญหาในการย้ายแผ่นไม้จำนวนมากขึ้น

เมื่อนักเรียนได้ปฏิบัติกิจกรรมแล้วให้บันทึกผลการย้ายแผ่นไม้ลงในตารางแล้วให้นักเรียนช่วยกันร่วมอภิปราย  แสดงความคิดเห็นเพื่อหาข้อสรุป  ซึ่งควรจะได้ดังนี้

จากตารางพบว่า

(1) ถ้ามีแผ่นไม้  1  แผ่น  เห็นอย่างชัดเจนว่าย้ายเพียงครั้งเดียวไปไว้ในหลักใดก็ได้

(2) ถ้ามีแผ่นไม้  2  แผ่น  จะต้องหยิบแผ่นไม้ย้ายอย่างน้อยที่สุด  3  ครั้ง

– ครั้งที่  1  ย้ายแผ่นที่  1  ไปไว้หลักที่ว่าง

– ครั้งที่  2  ย้ายแผ่นที่  2  ไปไว้หลักที่ว่าง

– ครั้งที่  3  ย้ายแผ่นที่  3  ไปไว้บนแผ่นที่  2

(3) ถ้ามีแผ่นไม้  3  แผ่น  วิธีที่จะทำให้จำนวนครั้งในการย้ายน้อยที่สุด  7  ครั้ง

– ครั้งที่  1  ย้ายแผ่นที่  1  ไปไว้หลักที่ว่าง

– ครั้งที่  2  ย้ายแผ่นที่  2  ไปไว้หลักที่ว่าง

– ครั้งที่  3  ย้ายแผ่นที่  1  ไปไว้บนแผ่นที่  2

– ครั้งที่  4  ย้ายแผ่นที่  3  ไปไว้หลักที่ว่าง

– ครั้งที่  5  ย้ายแผ่นที่  1  ไปไว้หลักที่ว่าง

– ครั้งที่  6  ย้ายแผ่นที่  2  ไปวางบนแผ่นที่  3

– ครั้งที่  7  ย้ายแผ่นที่  1  ไปวางบนแผ่นที่  2

จะเห็นว่าการย้ายแผ่นไม้  3  ครั้งแรกใช้วิธีการเดียวกับการย้ายแผ่นไม้  2  แผ่น  จากนั้นลองให้

นักเรียนหาจำนวนครั้งที่น้อยที่สุดในการย้ายแผ่นไม้ต่อไปอีก  โดยเพิ่มขึ้นเป็น  4,  5,  6,  7, ...

จากความสัมพันธ์ดังกล่าว  สามารถคาดเดาจำนวนครั้งที่น้อยที่สุดในการย้ายแผ่นไม้ต่อไปได้อีกดังนี้

จำนวนแผ่นไม้  1  แผ่น  จำนวนครั้งน้อยที่สุดในการย้ายคือ  1   หรือเขียนในรูป  2¹ – 1

จำนวนแผ่นไม้  2  แผ่น  จำนวนครั้งน้อยที่สุดในการย้ายคือ  2   หรือเขียนในรูป  2² – 1

จำนวนแผ่นไม้  3  แผ่น  จำนวนครั้งน้อยที่สุดในการย้ายคือ  3   หรือเขียนในรูป  2³ – 1

จำนวนแผ่นไม้  4  แผ่น  จำนวนครั้งน้อยที่สุดในการย้ายคือ  15  หรือเขียนในรูป  2⁴ – 1

จำนวนแผ่นไม้  5  แผ่น  จำนวนครั้งน้อยที่สุดในการย้ายคือ  31  หรือเขียนในรูป  2⁵ – 1

จำนวนแผ่นไม้  n  แผ่น  จำนวนครั้งน้อยที่สุดในการย้ายคือ   2ⁿ – 1

จากการจัดกิจกรรมดังกล่าว  จะเห็นว่าเป็นการส่งเสริมกระบวนการคิด  โดยผ่านการลงมือปฏิบัติจริง  จากการใช้ของเล่นเพื่อพัฒนากระบวนการแก้ปัญหา   เพื่อนำไปสู่การค้นพบจนสามารถสรุป   สร้างเป็นองค์ความรู้ได้

ข้อเสนอแนะ

ครูอาจให้นักเรียนสร้างอุปกรณ์การเล่น  โดยตัดกระดาษแข็งเป็นรูปวงกลม  หรือรูปสี่เหลี่ยมจัตุรัสลดหลั่นกันเป็นลำดับ  แล้วใช้วางบนโต๊ะใน  3  ตำแหน่ง  แทนการสร้างของเล่นแบบถาวรก็ได้