แบบรูปของพัฒนาการทางความคิดในวิชาเรขาคณิตเป็นผลงานของนักคณิตศาสตร์ศึกษา สองสามีภรรยา คือ Dina van Hiele-Geldof และ Pierre Marie van Hiele โดยที่ทั้งสองพยายามหาคำตอบว่าทำไมผลสัมฤทธิ์ของการเรียนวิชาเรขาคณิตต่ำ นักเรียนไม่เข้าใจเนื้อหาและพิสูจน์ได้ไม่ดี แบบรูปของแวนฮีลีเป็นที่ยอมรับกันว่าสามารถใช้เป็นแนวทางในการสอน และการประเมินความสามารถของนักเรียนในวิชาเรขาคณิตได้ดี

     แบบรูปของแวนฮีลีเป็นผลมาจากวิทยานิพนธ์ในระดับปริญญาเอกที่เสนอต่อมหาวิทยาลัยยูเทรคต์ (Utrecht) ประเทศเนเธอร์แลนด์ ในปี ค.ศ. 1957 โดยที่ Pierre ได้วิจัยทางด้านทฤษฎีของพัฒนาการทางความคิด ส่วน Dina ได้ศึกษาทางด้านวิธีสอน เพื่อยกระดับความคิดจากระดับหนึ่งไปอีกระดับหนึ่ง หลังจากการเสนอวิทยานิพนธ์ได้ไม่นาน Dina ได้เสียชีวิต Pierre จึงได้พัฒนาทฤษฎีต่อไป

     ประเทศสหภาพสาธารณรัฐสังคมนิยมโซเวียตสนใจงานวิจัยนี้ จึงวิจัยซ้ำเพื่อทดสอบความถูกต้อง (Validate) และ ศึกษารายละเอียดเพิ่มเติม โดยพิกาโลและสโตลยา (Pyshkalo and Stolyar) จากสถาบันด้านการสอนของโซเวียต (Soviet Academy of Pedagogical Science) เป็นผู้วิจัย และประเทศสหภาพสาธารณรัฐสังคมนิยมโซเวียตได้ปรับปรุงหลักสูตร เรขาคณิตอย่างได้ผลดีในช่วงปี ค.ศ. 1960–1969 งานของแวนฮีลีได้รับความสนใจจากนักคณิตศาสตร์ศึกษาในสหรัฐอเมริกา เนื่องจากบทความของ Izaak Wirszup (1976) ชื่อ Breakthroughs in Psychology of Learning and Teaching Geometry และจากผลงานชิ้นประวัติศาสตร์ของอาจารย์ของแวนฮีลีจากมหาวิทยาลัยยูเทรคต์ คือ ศาสตราจารย์ Hans Freudenthal ในหนังสือชื่อ Mathematics as an Educational Task จากนั้นจึงมีการศึกษาวิจัยแบบรูปนี้อย่างจริงจัง มีงานวิจัยออกมา มากมายและทฤษฎีมีความชัดเจนมากขึ้น แบบรูปของพัฒนาการทางความคิดในวิชาเรขาคณิตประกอบด้วย

          1. แบบรูป (The Model)

          2. สมบัติของแบบรูป (Properties of the Model)

          3. ขั้นตอนต่างๆ ของการเรียนรู้ (Phases of Learning)

แบบรูป (The Model)

     แบบรูปของพัฒนาการทางความคิดในวิชาเรขาคณิตของแวนฮีลีประกอบด้วยระดับความคิดทางเรขาคณิตรวม 5 ระดับ จากระดับ 0 ถึงระดับ 4 ดังนี้

ระดับ 0 การเห็นภาพ (Visualization)

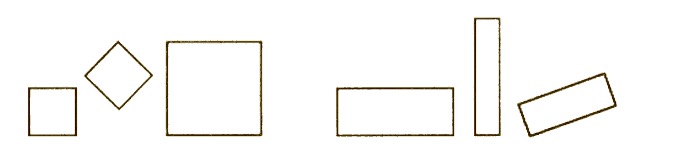
     ในระดับนี้ ผู้เรียนรับรู้ว่าอวกาศ (Space) เป็นสิ่งที่อยู่รอบตัว มโนทัศน์ทางเรขาคณิตต่างๆ จะรับรู้ในลักษณะภาพรวม มากกว่าแยกส่วนหรือลักษณะ เช่น รูปทางเรขาคณิตจะรับรู้ทั้งรูป ไม่แยกเป็นส่วนๆ เป็นด้าน มุม หรือสมบัติของรูป ผู้ที่มีความคิดในระดับนี้สามารถเรียนคำศัพท์ทางเรขาคณิต บอกชื่อรูปได้ เมื่อให้ดูรูปจะสร้างรูปบนกระดานตะปู หรือวาดรูปคร่าวๆ ได้ เมื่อให้รูปสี่เหลี่ยมจัตุรัสและสี่เหลี่ยมผืนผ้าดังรูปข้างล่าง สามารถบอกได้ว่ารูปใดเป็นรูปสี่เหลี่ยมจัตุรัสหรือรูปสี่เหลี่ยมผืนผ้า เพราะมีลักษณะคล้ายรูปที่เคยเห็นมาก่อน แต่ไม่สามารถบอกได้ว่ามีมุมฉากสี่มุม หรือด้านตรงข้ามขนานกัน

ระดับ 1 การวิเคราะห์ (Analysis)

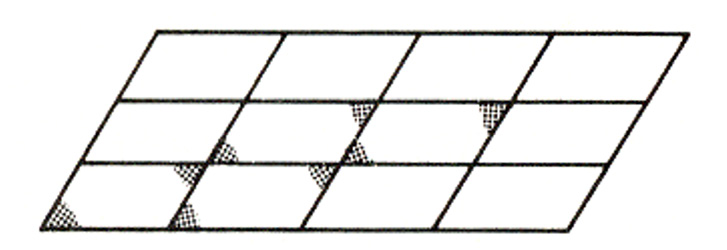
     ในระดับนี้ผู้เรียนเริ่มมีการวิเคราะห์มโนทัศน์ทางเรขาคณิต เช่น จากการสังเกต จากการทดลอง ผู้เรียนเริ่มสนใจเกี่ยวกับลักษณะของรูป สมบัติต่างๆ ที่ค่อยๆ ก่อตัว ทำให้สามารถแยกรูปชนิดต่างๆ ได้ จะมองรูปทางเรขาคณิตแบบแยกส่วนได้ จะบอกได้ว่าเป็นรูปใดโดยดูจากส่วนต่างๆ ของรูป เช่น เมื่อให้ดูรูปสี่เหลี่ยมด้านขนานดังภาพ สามารถระบายสีมุมที่เท่ากันได้ บอกได้ว่ามุมตรงข้ามเท่ากัน สามารถบอกลักษณะทั่วไปของสี่เหลี่ยมด้านขนานได้ แต่ยังไม่สามารถอธิบายความสัมพันธ์ระหว่างสมบัติได้ ยังไม่เห็นความสัมพันธ์ระหว่างรูปหนึ่งกับอีกรูปหนึ่ง และยังไม่เข้าใจบทนิยาม

ระดับ 2 การอนุมานอย่างไม่เป็นทางการ (Informal Deduction)

     ในระดับนี้ ผู้เรียนสามารถสร้างความสัมพันธ์ระหว่างสมบัติของรูปได้ทั้งภายในรูป (เช่น ในรูปสี่เหลี่ยมที่มีด้านตรงข้ามขนานกัน 2 คู่ มุมตรงข้ามจะเท่ากัน) และระหว่างรูป (เช่น รูปสี่เหลี่ยมจัตุรัสเป็นรูปสี่เหลี่ยมมุมฉาก มีสมบัติต่างๆ ของสี่เหลี่ยมมุมฉากครบ) ดังนั้น นักเรียนสามารถสรุปสมบัติต่างๆ ของรูปได้ และแยกรูปเป็นกลุ่มๆ ได้ตามสมบัติ สามารถเข้าใจสิ่งที่เรียกว่า Class Inclusion ได้ เช่น สามเหลี่ยมด้านเท่าทุกรูปเป็นสามเหลี่ยมหน้าจั่ว สามารถเข้าใจนิยามได้เป็นอย่างดี สามารถติดตามการให้เหตุผลอย่างไม่เป็นทางการ (Informal Argument) ได้ และสามารถให้เหตุผลอย่างไม่เป็นทางการได้ อย่างไรก็ตาม ผู้เรียนในระดับนี้ยังไม่เข้าใจการอนุมาน (Deduction) โดยรวมได้ทั้งหมด ไม่เข้าใจบทบาทของสัจพจน์ ไม่เข้าใจว่าการให้เหตุผลอาจสับเปลี่ยนแนวทางได้ และไม่เข้าใจการพิสูจน์ที่เริ่มต้นจากสิ่งที่กำหนดให้ที่แตกต่างออกไปหรือไม่คุ้นเคย

ระดับ 3 การอนุมาน (Deduction)

     ในระดับนี้ ผู้เรียนเข้าใจบทบาทของการอนุมานว่าเป็นหนทางในการสร้างทฤษฎีต่างๆ ทางเรขาคณิตตามกรอบของระบบสัจพจน์ ผู้เรียนเห็นความสัมพันธ์ระหว่าง อนิยาม นิยาม สัจพจน์ ทฤษฎี และการพิสูจน์ ผู้เรียนไม่เพียงแต่จดจำการพิสูจน์ แต่ยังพิสูจน์เป็น มองเห็นความเป็นไปได้ที่จะหาวิธีพิสูจน์มากกว่า 1 วิธี เข้าใจเงื่อนไขที่จำเป็นและเพียงพอ (Necessary and Sufficient Condition) เข้าใจความแตกต่างระหว่างทฤษฎีบทและบทกลับ

ระดับ 4 ความชัดแจ้ง (Rigor)

     ในระดับนี้ ผู้เรียนสามารถเข้าใจและสามารถเปรียบเทียบระบบสัจพจน์ที่แตกต่างกันได้ เข้าใจ Non-Euclidean Geometry สามารถมองเรขาคณิตในลักษณะที่เป็นนามธรรมได้

     ระดับที่ 4 นี้ เป็นระดับที่ได้รับการพัฒนาจากแวนฮีลี น้อยที่สุด จากการสนทนาเป็นส่วนตัวกับ Alan Hoffer เมื่อวันที่ 25 กุมภาพันธ์ ค.ศ. 1985 P.M. van Hiele กล่าวว่าเขาสนใจในระดับ 0 ถึงระดับ 3 เพราะเรขาคณิตในโรงเรียนจะสอนถึงระดับที่ 3 เท่านั้น

สมบัติของแบบรูป (Properties of the Model)

     นอกเหนือจากการค้นพบลักษณะพฤติกรรมในแต่ละระดับของแบบรูปแล้ว แวนฮีลียังได้พบสมบัติบางประการของแบบรูปอีกดังนี้

     1. การมีลำดับ (Sequential) ผู้เรียนจะพัฒนาไปตามระดับความคิด ผู้ที่มีระดับความคิดที่ n จะต้องมีระดับความคิดที่ n – 1 มาก่อน ไม่สามารถข้ามระดับได้

     2. ความก้าวหน้า (Advancement) การพัฒนาจากระดับความคิดหนึ่งไปสู่ระดับถัดไป ขึ้นอยู่กับเนื้อหาและวิธีการสอนมากกว่าขึ้นอยู่กับอายุ ไม่มีวิธีการสอนใดที่ทำให้นักเรียนสามารถข้ามระดับได้

     3. สิ่งที่เกิดขึ้นภายในและสิ่งที่เกิดขึ้นภายนอก (Intrinsic and Extrinsic) สิ่งซึ่งไม่ชัดเจนในระดับหนึ่ง จะปรากฏชัดเจนในระดับต่อไป เช่น ในระดับ 0 ผู้เรียนรับรู้โดยพิจารณาจากรูปร่าง การกำหนดรูปจากสมบัติยังไม่ชัดเจน จนกว่าจะมีระดับความคิดในระดับ 1 ซึ่งจะมีการวิเคราะห์รูป องค์ประกอบ และสมบัติต่างๆ

     4. การมีภาษาประจำระดับ (Linguistics) แต่ละระดับมีภาษาเป็นของตนเองที่เชื่อมโยงความสัมพันธ์ของสิ่งต่างๆ เข้าด้วยกัน ความสัมพันธ์ที่ถือว่าถูกต้องในระดับหนึ่ง อาจถูกขยายความหรือนิยามใหม่ในอีกระดับ เช่น รูปหนึ่งๆ อาจมีชื่อเรียกได้มากกว่า 1 ชื่อ (รูปสี่เหลี่ยมจัตุรัสอาจเรียกว่าเป็นรูปสี่เหลี่ยมมุมฉาก) ผู้ที่อยู่ในระดับ 1 จะไม่เข้าใจแนวคิดที่เรียกว่า Class Inclusion

     5. การไม่เข้ากัน (Mismatch) ผู้เรียนที่มีระดับความคิดระดับใดระดับหนึ่ง หากได้รับการสอนด้วยแนวคิดที่สูงกว่าระดับความคิดของตน ผู้เรียนจะไม่เข้าใจ ไม่เกิดการเรียนรู้อย่างถูกต้อง และไม่สามารถติดตามกระบวนการคิดที่สอนอยู่ได้

สมบัติของแบบรูป (Properties of the Model)

     นอกเหนือจากการค้นพบลักษณะพฤติกรรมในแต่ละระดับของแบบรูปแล้ว แวนฮีลียังได้พบสมบัติบางประการของแบบรูปอีกดังนี้

     1. การมีลำดับ (Sequential) ผู้เรียนจะพัฒนาไปตามระดับความคิด ผู้ที่มีระดับความคิดที่ n จะต้องมีระดับความคิดที่ n – 1 มาก่อน ไม่สามารถข้ามระดับได้

     2. ความก้าวหน้า (Advancement) การพัฒนาจากระดับความคิดหนึ่งไปสู่ระดับถัดไป ขึ้นอยู่กับเนื้อหาและวิธีการสอนมากกว่าขึ้นอยู่กับอายุ ไม่มีวิธีการสอนใดที่ทำให้นักเรียนสามารถข้ามระดับได้

     3. สิ่งที่เกิดขึ้นภายในและสิ่งที่เกิดขึ้นภายนอก (Intrinsic and Extrinsic) สิ่งซึ่งไม่ชัดเจนในระดับหนึ่ง จะปรากฏชัดเจนในระดับต่อไป เช่น ในระดับ 0 ผู้เรียนรับรู้โดยพิจารณาจากรูปร่าง การกำหนดรูปจากสมบัติยังไม่ชัดเจน จนกว่าจะมีระดับความคิดในระดับ 1 ซึ่งจะมีการวิเคราะห์รูป องค์ประกอบ และสมบัติต่างๆ

     4. การมีภาษาประจำระดับ (Linguistics) แต่ละระดับมีภาษาเป็นของตนเองที่เชื่อมโยงความสัมพันธ์ของสิ่งต่างๆ เข้าด้วยกัน ความสัมพันธ์ที่ถือว่าถูกต้องในระดับหนึ่ง อาจถูกขยายความหรือนิยามใหม่ในอีกระดับ เช่น รูปหนึ่งๆ อาจมีชื่อเรียกได้มากกว่า 1 ชื่อ (รูปสี่เหลี่ยมจัตุรัสอาจเรียกว่าเป็นรูปสี่เหลี่ยมมุมฉาก) ผู้ที่อยู่ในระดับ 1 จะไม่เข้าใจแนวคิดที่เรียกว่า Class Inclusion

     5. การไม่เข้ากัน (Mismatch) ผู้เรียนที่มีระดับความคิดระดับใดระดับหนึ่ง หากได้รับการสอนด้วยแนวคิดที่สูงกว่าระดับความคิดของตน ผู้เรียนจะไม่เข้าใจ ไม่เกิดการเรียนรู้อย่างถูกต้อง และไม่สามารถติดตามกระบวนการคิดที่สอนอยู่ได้

ขั้นตอนของการเรียนรู้ (Phases of Learning)

     งานวิจัยของแวนฮีลีระบุว่า การยกระดับความคิดทางเรขาคณิตจากระดับหนึ่งไปสู่อีกระดับหนึ่ง ขึ้นอยู่กับการสอนมากกว่าอายุ ดังนั้น วิธีการสอนและการวางลำดับการสอน เนื้อหา และวัสดุอุปกรณ์ที่ใช้จึงมีความสำคัญ เพื่อตอบคำถามเกี่ยวกับ "การสอนเพื่อยกระดับความคิด" ไดนา (Dina) จึงได้ทำการวิจัยเพื่อหาวิธีการสอนที่จะยกระดับความคิดจากระดับ 1 สู่ระดับ 2 และได้สรุปเป็น 5 ขั้นตอน (Phases) ในที่นี้จะใช้กิจกรรมเกี่ยวกับ รูปสี่เหลี่ยมขนมเปียกปูนเป็นตัวอย่าง

Phase 1 (Inquiry/Information)

     ขั้นนี้ผู้สอนและนักเรียนสนทนาและทำกิจกรรมร่วมกันเกี่ยวกับสิ่งที่จะเรียน ระดับนี้มีการสังเกต ทบทวนมโนทัศน์ที่เกี่ยวข้อง ถาม-ตอบ เช่น รูปสี่เหลี่ยมขนมเปียกปูนคืออะไร รูปสี่เหลี่ยมจัตุรัสคืออะไร รูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยม จัตุรัสใช่หรือไม่ รูปสี่เหลี่ยมจัตุรัสเป็นรูปสี่เหลี่ยมขนมเปียกปูนใช่หรือไม่ ทำไมนักเรียนจึงกล่าวเช่นนั้น จุดมุ่งหมายของกิจกรรม ในขั้นนี้คือ

     1. เพื่อให้ผู้สอนรู้พื้นฐานเกี่ยวกับเรื่องที่นักเรียนจะเรียน

     2. นักเรียนได้รู้ตัวว่าจะเรียนหัวข้อใดและแนวทางของการเรียนในหัวข้อนี้เป็นอย่างไร

Phase 2 (Directed Orientation)

     ขั้นนี้นักเรียนเริ่มศึกษาหัวข้อที่จะเรียนจากเอกสารหรือกิจกรรมที่ผู้สอนได้จัดลำดับไว้เป็นตอน ๆ กิจกรรมเหล่านี้จะแสดง ให้นักเรียนเห็นถึงลักษณะและโครงสร้างของสิ่งที่จะเรียนในระดับนี้ ดังนั้น เนื้อหาและกิจกรรมจะสั้นเพื่อให้นักเรียนตอบคำถาม เฉพาะอย่าง เช่น ผู้สอนให้นักเรียนใช้กระดานตะปูเพื่อสร้างรูปสี่เหลี่ยมขนมเปียกปูนที่มีเส้นทแยงมุมเท่ากัน สร้างรูปสี่เหลี่ยม ขนมเปียกปูนที่มีลักษณะดังกล่าวแต่เล็กกว่า ใหญ่กว่า สร้างรูปสี่เหลี่ยมขนมเปียกปูนที่มีมุมฉากสี่มุม มีมุมฉากสามมุม สองมุม หรือหนึ่งมุม

Phase 3 (Explication)

     จากประสบการณ์ในตอนที่แล้ว นักเรียนจะสามารถแสดงความคิดเห็นและแลกเปลี่ยนความคิดหรือความเข้าใจเกี่ยวกับ ความสัมพันธ์ที่ได้จากการสังเกต บทบาทของผู้สอนจะน้อยลงในขั้นนี้ เว้นแต่จะช่วยให้นักเรียนใช้ภาษาได้ถูกต้องเหมาะสม ในขั้นตอนนี้ ระบบความสัมพันธ์ของสิ่งต่าง ๆ จะเกิดขึ้นและค่อย ๆ ชัดขึ้น ในกรณีของสี่เหลี่ยมขนมเปียกปูน นักเรียนจะสามารถอภิปรายกันเอง หรือกับผู้สอนว่าเป็นรูปใด มีสมบัติใด ความสัมพันธ์เป็นอย่างไร สังเกตได้จากการทำกิจกรรม

Phase 4 (Free Orientation)

     ในขั้นนี้ผู้สอนจะให้นักเรียนทำกิจกรรมหรืองานที่ซับซ้อนมากขึ้น เป็นกิจกรรมที่มีหลายขั้นตอน ทำได้หลายวิธี และ บางครั้งเป็นกิจกรรมปลายเปิด (Open-Ended Task) นักเรียนต้องสร้างหรือหาวิธีการเอาเอง นักเรียนจะได้ประสบการณ์ ในการหาวิธีการของตนเองที่จะทำงานให้เสร็จ การทำเช่นนี้จะนำไปสู่การสำรวจ (Investigation) และทำให้ความสัมพันธ์ของ สิ่งต่าง ๆ ที่เรียนชัดเจนมากขึ้นอย่างเห็นได้ชัด เช่น กิจกรรมให้นักเรียนพับครึ่งกระดาษแผ่นหนึ่งแล้วพับครึ่งอีกครั้งหนึ่ง แล้ว ตัดมุมดังรูป

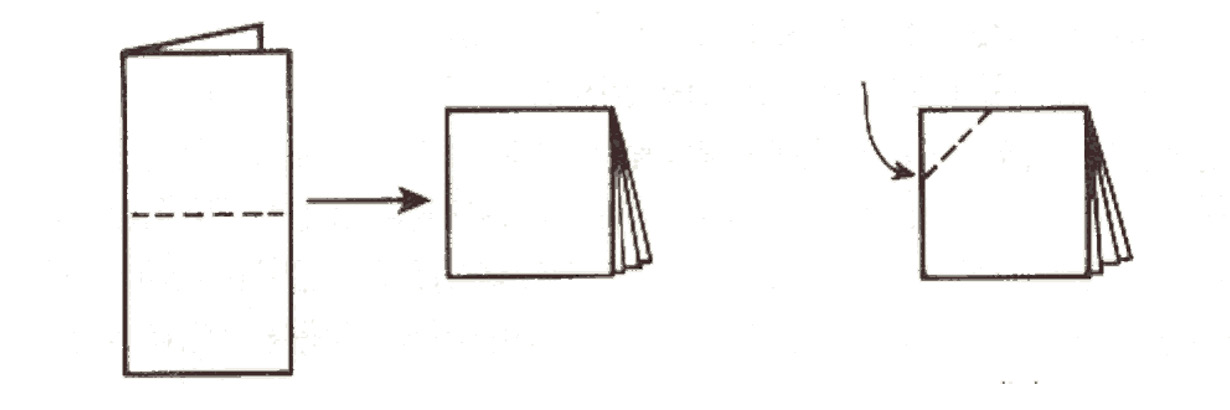
     ให้นักเรียนจินตนาการก่อนตัดมุมว่าเมื่อคลี่กระดาษแล้วจะได้รูปใด ให้ อธิบายคำตอบ เส้นทแยงมุมของรูปที่ตัดออกมา จะเป็นอย่างไร จุดตัดกันของเส้นทแยงมุมจะอยู่ที่ใด ทำไมพื้นที่ของสี่เหลี่ยมขนมเปียกปูนจึงเป็นครึ่งหนึ่งของผลคูณของเส้นทแยงมุม

Phase 5 (Integration)

     ในขั้นนี้นักเรียนจะทบทวนและสรุปสิ่งที่ได้เรียนมาแล้ว เพื่อให้เห็นภาพรวมของความสัมพันธ์ของสิ่งที่เรียนไปแล้ว ผู้สอนมีหน้าที่ช่วยในการสังเคราะห์เพิ่มเติมภาพรวมที่ได้เรียนไปแล้ว ให้สังเกตว่าในขั้นนี้จะไม่มีการเสนอสิ่งใหม่ ๆ จะมีเพียงการสรุป ความเป็นมาของสมบัติเหล่านั้น

     เมื่อจบขั้นที่ 5 นักเรียนจะมีระดับการคิดไปสู่ขั้นใหม่ ระดับการคิดใหม่จะไปปรับระดับความคิดเดิม นักเรียนก็พร้อมที่จะรับประสบการณ์เพื่อก้าวไปสู่ระดับความคิดในขั้นถัดไป

บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ปีที่ 51 ฉบับที่ 244 กันยายน – ตุลาคม 2566

ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://emagazine.ipst.ac.th/244/32/

บรรณานุกรม

National Council of Teachers of Mathematics. (1987). Learning and Teaching Geometry, K-12. Reston, Va: National Council of Teachers of Mathematics