และแล้วก็ถึงฤดูฝน... นี่คือคำพูดที่นึกถึงอยู่ในใจตลอดเวลา นับตั้งแต่ฝนเริ่มตกครั้งแรกๆ ในเดือน พฤษภาคม แล้วจะค่อยๆ ตกหนักขึ้น เรื่อยไปจนถึงปลายฝนต้นหนาวราวๆ เดือนตุลาคม ในกรุงเทพฯ การที่ฝนตกมีส่วนดีตรงที่ช่วยลดความร้อนที่เก็บสะสมไว้ในคอนกรีต ทำให้อากาศในกรุงเทพฯ เย็นขึ้นมาบ้าง แต่จะแย่ก็ตรงที่ ฝนตกได้ซ้ำเติมปัญหาจราจรติดขัดให้เลวร้ายยิ่งขึ้นไปอีก การยืนรอรถเมล์(หรือรถตู้) อยู่ข้างถนนที่รถแน่นเอี๊ยด ซ้ำร้าย สายฝนยังตกกระหน่ำซ้ำลงมาราวกับพระพิรุณทำโอที (over time) เหล่านี้คือเหตุการณ์ที่หลายๆ คนต้องเคยประสบมาแล้วเป็นแน่แท้

บ่อยครั้งที่ฝนตกคือการซ้ำเติมปัญหาจราจรติดขัดในกรุงเทพฯ
รูปจาก http://www.mumuu.com

หากวันหนึ่งฝนตกลงมาขณะที่เรากำลังอยู่นอกอาคาร และวันนั้นดันลืมพกร่มติดตัวไปด้วย สถานะการณ์นี้ สิ่งที่ทุกๆ คนทำคือวิ่งหลบฝนไปยังที่ร่มให้เร็วที่สุดเท่าที่จะทำได้ เพื่อที่เราจะไม่เปียกฝนมากเกินไป นี่คือการแก้ปัญหาเฉพาะหน้าที่ดีที่สุดอย่างไม่ต้องสงสัย

แม้จะรู้ทั้งรู้ว่าการวิ่งเข้าที่ร่มเพื่อหลบฝนที่กำลังโปรยปลายลงมา น่าจะเป็นวิธีที่ทำให้เปียกน้อยที่สุด แต่ในวงการวิทยาศาสตร์กลับมีคนตั้งข้อสงสัยว่า “การวิ่งหลบฝนเข้าที่ร่มให้เร็วที่สุดนั้น ดีที่สุดแล้วแน่หรือ?” เพราะมันมีข้อโต้แย้งที่ว่า “ถ้าหากคุณวิ่ง ตัวคุณจะมีพื้นที่รับน้ำมากกว่าคุณเดิน!! ซึ่งอาจเป็นสาเหตุทำให้การวิ่งเปียกมากกว่าการเดินก็เป็นได้” จากข้อโต้แย้งนี้ ทำให้เกิดกระบวนการทางวิทยาศาสตร์เพื่อพิสูจน์ให้รู้ชัดไปเลยว่า “เดินหลบฝน หรือ วิ่งหลบฝน ทำอย่างไหนจึงเปียกน้อยกว่ากัน”

วิ่งหลบฝนเข้าที่กำบังเป็นวิธีที่ดีที่สุด แน่ใจหรือ?

กระบวนการทางวิทยาศาสตร์สำหรับปัญหา “วิ่งหรือเดินหลบฝน” นี้ เท่าที่สืบค้นมา จะเน้นไปที่การคำนวณเสียเป็นส่วนใหญ่ มีการทดลองบ้าง แต่ไม่ค่อยทำกับจริงจังเท่าไร (คือไม่ได้ทดลองจริงจังเหมือนอย่าง CERN ค้นหาฮิกส์โบซอน) การคำนวณก็เริ่มตั้งแต่แบบจำลองง่ายๆ ไปจนถึงแบบจำลองที่ซับซ้อน (วัตถุ n มิติ วิ่งหลบฝนที่ตกลงบนพื้นที่ n - 1 มิติ... เลอะเทอะไปกันใหญ่ล่ะ)

อย่างไรก็ตาม ผลสรุปของการศึกษานี้สนับสนุนว่า การวิ่งหลบฝนเป็นวิธีที่ทำให้เปียกน้อยกว่าการเดิน

เรื่องราวของ "วิ่งหรือเดินหลบฝน" นี้ถูกพูดถึงครั้งแรกในปี พ.ศ. 2518 โดย Jearl Walker เขียนลงหนังสือ The Flying Circus of Physics แต่เป็นเพียงข้อคิดเห็นโดยไม่มีการพิสูจน์ทั้งทางการทดลองหรือทางคณิตศาสตร์ เขาเสนอว่า หากเขาจำเป็นต้องวิ่งเข้าที่ร่มหลบฝน เขาเลือกที่จะวิ่งให้เร็วที่สุดเท่าที่จะทำได้ จากนั้นก็ไม่มีใครกล่าวถึงปัญหานี้อีกจนกระทั่งปัญหาดังกล่าวถูกเขียนเป็นคำถามในหนังสือ New Scientist magazine ฉบับปี 1995 (พ.ศ.2538) มีผู้อ่านวารสารหลายคนร่วมแสดงความคิดเห็น มีความคิดเห็นที่น่าใจในเชิงวิชาการ ดังนี้

ว่าด้วยเรื่องของทิศทางลม เป็นของ Matthew Wright จาก มหาวิทยาลัย University of Southampton ซึ่ง Matthew ได้รวมแนวคิดเรื่องทิศทางลม นึกภาพว่าหากฝนตกโดยที่ไม่มีลม หยดน้ำจะตกจากฟ้าลงตรงๆ ถ้าหากมีลมพัด (น่าจะหมายถึงลมพัดในแนวระดับ) น้ำฝนจะตกลงแนวเฉียงแทน เพราะลมพัดให้หยดน้ำเคลื่อนที่ในแนวระดับด้วย แล้วเสนอแนวคิดที่สนับสนุนข้อเสนอของ Jearl โดยกล่าวว่า "ในกรณีที่ฝนตกลงในแนวเฉียงเข้าปะทะกับด้านหน้า เราควรจะวิ่งให้เร็วที่สุดเท่าที่จะทำได้ ส่วนกรณีที่ฝนตกในแนวเฉียงปะทะกับด้านหลัง เราควรวิ่งให้เร็วเท่าๆ กับความเร็วในแนวราบของน้ำฝน"

ฝนตกแบบมีลมพัด หยดน้ำจะตกแบบเฉียงๆ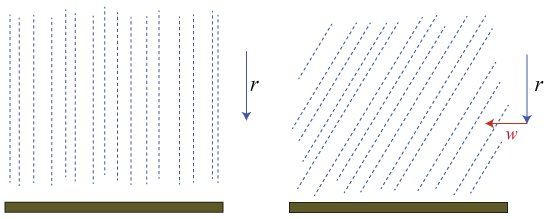

รูปสำหรับอธิบาย r คือความเร็วฝนในแนวดิ่ง และ w คือความเร็วลม

การพิจารณาจากความแห้ง ของ Mike Stevenson โดยเสนอว่า "เราควรพิจารณาความเปียกจากเวลาที่ทำให้ตัวเราแห้ง หากคราวใดที่เราตากฝนแล้วเปียกมาก นั้นหมายความว่า มีน้ำมาเกาะที่ตัวเรามาก ซึ่งต้องใช้เวลายืนตากลมและผึ่งแดดในที่ร่มนาน กว่าตัวเราจะแห้ง ในทางกลับกันถ้าตัวเราเปียกฝนน้อย เราจะใช้เวลาตากลมผึ่งแดดน้อยกว่า" และแสดงความคิดคิดสนับสนุน Jearl ว่า "เราควรจะวิ่งหลบฝนให้เร็วที่สุด เพราะทำให้เวลาที่เราต้องอยู่ตากฝนน้อยลง แล้วน้ำจะมาเกาะที่ต้วเราน้อยลง และจะเปียกน้อยลง"

ความเปียกนิยามเป็นปริมาณน้ำที่เกาะหรือซึมในคนที่วิ่งตากฝน หากมีน้ำเกาะอยู่มากย่อมหมายถึงเปียกมาก และต้องใช้เวลานานกว่าตัวจะแห้ง

ภายหลังแนวคิดทั้งสองนี้ถูกรวมเข้าไปในแบบจำลองทางคณิตศาสตร์ โดย นิยามความเปียกตามความคิดของ Mike และในปี พ.ศ. 2552 วารสาร Mathematics Magazine ได้ตีพิมพ์เอกสารของ Dank Hailman และคณะ ในแบบจำลองของ Denk ได้คำนึงถึงทิศทางลมแนวคิดของ Matthew ด้วย เราจะได้เห็นแบบจำลองนี้กันในหน้าถัดไป

พิสูจน์ด้วยแบบจำลอง

ความคิดเห็นเรื่องความเปียกของ Mike ถือนิยามที่ง่ายที่สุด แต่การนำไปใช้ในทางทฤษฎีก็ค่อยไม่สมจริง ยกตัวอย่างเช่น ถ้ามีคนสองคนยืนอยู่นิ่งๆ แล้วเทน้ำ 50 ลิตร และ 100 ลิตร ใส่คนที่หนึ่งและคนที่สองตามลำดับ กรณีดังนี้ ผลคำนวณจะบอกว่าความเปียกต่างกัน คนที่หนึ่งจะเปียกน้อยความคนที่สอง ซึ่งในความเป็นจริงแล้ว คนทั้งสองเปียกโชกเหมือนๆ กัน ซึ่งคนทั้งสองจะใช้เวลารอให้แห้งพอๆ กัน

ในแบบจำลองทางคณิตศาสตร์ สำหรับ "วิ่งหรือเดินหลบฝน" ถูกเสนอในปี พ.ศ. 2542 โดยคณะ HBHP ที่มีนักอุตุนิยมวิทยา 4 ท่าน ได้แก่ Holden, Belcher, Horvath และ Pytharoulis แนวคิดของ HBHP คือสมมุติว่ามีคนหนึ่งกำลังวิ่งหลบฝน จะถือให้รูปร่างของคนคนนี้เป็นกล่องสี่เหลี่ยม และจะถือว่าฝนจะตกลงสู่กล่อง (คน) อย่างสม่ำเสมอด้วยความเร็วคงที่ ดังรูป เพื่อความครบถ้วนสมบูรณ์ ในบทความนี้จะขอกำหนดตัวแปรไว้ดังนี้ ให้ s คือ อัตราเร็วในแนวระดับหรือแนวราบของกล่องที่กำลังเคลื่อนที่ และจะถือว่าคนจะต้องวิ่งในระยะทาง L จึงจะเข้าที่ร่มได้ จากนั้นกำหนดให้ r คือ อัตราเร็วของฝนที่กำลังตกลงมาตรงๆ ในแนวดิ่ง ในกรณีที่ฝนตกลมพัด จะถือว่าน้ำฝนจะมีอัตราเร็วในแนวระดับ w เพิ่มเติมจากอัตราเร็วในแนวดิ่ง r ด้วย

รูปแสดงตัวอย่างฝนตกแบบมีลมพัด

เมื่อกำหนดตัวแปรเสร็จแล้ว ต่อไปจะเป็นการอธิบายสิ่งที่เกิดขึ้น ขั้นต้นให้พิจารณากรณีที่ฝนตกในแนวดิ่งและไม่มีลมพั (w = 0) สิ่งที่เกิดขึ้นสามารถแยกเป็นข้อได้ดังนี้
1. กรณีที่กล่องอยู่นิ่งๆ กล่องจะมีพื้นที่รับน้ำตรงฝากล่องด้านบนเท่านั้น
2. หากกล่องเคลื่อนที่ไปด้านหน้า ปริมาตรด้านหน้าของกล่องจะเข้าไปแทนที่ปริมาตรของน้ำฝน เสมือนกับว่ากล่องมีพื้นที่รับน้ำเพิ่มขึ้น ทำให้กล่องมีแนวโน้มจะเปียกมากยิ่งขึ้น 
3. สำหรับกรณีที่กล่องไม่เคลื่อนที่ เนื่องจากแบบจำลองควบคุมระยะไม่ใช่ควบคุมเวลา ดังนั้นตราบใดที่กล่องไม่เคลื่อนที่จนครบระยะทาง L กล่องก็จะต้องตากฝนไปเรื่อยๆ ทำให้กล่องเปียกอย่างมาก
4. ถ้ากล่องเคลื่อนที่ กล่องจะใช้เวลาตากฝนน้อยลง กล่องก็จะควรจะเปียกน้อยลง

ถ้าลองดูดีๆ ข้อ 2. กับข้อ 4. เป็นผลที่ตรงข้ามกันและกัน พูดง่ายๆ คือ ถ้ากล่องเคลื่อนที่ กล่องจะมีพื้นที่รับน้ำมากขึ้นแต่ก็ใช้เวลาตากฝนน้อยลง การคำนวณของ HBHP แสดงผลออกมาว่า ผลตามข้อ 4. มีอิทธิพลเหนือกว่า ความเปียกที่จะลดลงตามข้อ 4. หักล้างความเปียกที่จะเพิ่มขึ้นตามข้อ 2. ได้ ทำให้ได้ข้อสรุปตามแบบจำลองนี้ว่า ยิ่งกล่องเคลื่อนที่เร็วมากเท่าไร กล่องยิ่งเปียกน้อยลงเท่านั้น ในที่สุด หากกล่องเคลื่อนที่ด้วยความเร็วอนันต์ กล่องจะเปียกน้อยที่สุด (ไม่ใช่ว่าจะแห้งสนิทแต่เปียกบ้าง)

ในเวลาต่อมา Dank ได้เพิ่มเติมแบบจำลอง HBHP โดยการพิจารณาความเร็วของลม พร้อมทั้งเปลี่ยนมุมมองการอธิบาย เพื่อได้มุมมองที่ดูเข้าใจง่ายกว่า สมมุติว่าตัวเราตอนนี้กำลังวิ่งฝ่าฝนที่กำลังตกลงในแนวดิ่ง (กรณีที่ยังไม่มีลม) ขอให้คิดว่า เราที่เป็นคนวิ่งรู้สึกเหมือนเราไม่เคลื่อนที่ แต่ฝนจะตกลงแบบเฉียงๆ เข้าหาตัวเรา (แม้จะไม่มีลมก็ตาม) ดังรูป ในมุมมองนี้ จะปรากฏบริเวณที่เรียกว่า "บริเวณฝน" น้ำฝนที่อยู่ใน "บริเวณฝน" จะตกลงใส่ตัวเรา (คน หรือ กล่อง) อย่างแน่นอน และเฉพาะฝนที่อยู่ใน "บริเวณฝน" เท่านั้นที่จะตกโดนกล่อง "บริเวณฝน" จะมีหน้าตาคล้ายท่อ หรือเสา วางตัวเอียงๆ พื้นที่หน้าตัดแตกต่างกันไปตามรูปร่างของกล่อง (คน) เช่น ถ้ากล่องคือกล่องทรงเหลี่ยม พื้นที่หน้าตัดของ "บริเวณฝน" จะเป็นพื้นที่สี่เหลี่ยม หรือ ถ้าเปลี่ยนจากกล่องเป็นทรงรี พื้นที่หน้าตัดของ "บริเวณฝน" จะเป็นวงรี เป็นต้น

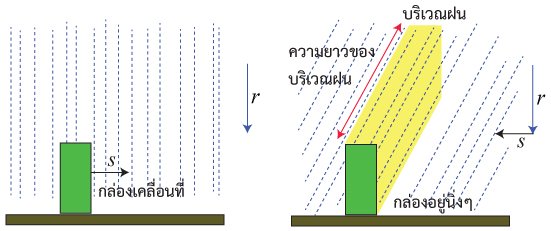
รูปซ้ายคือสถานะการณ์ในมุมมองปกติ ส่วนรูปขวาคือมุมมองที่กล่องอยู่นิ่ง ตามแบบจำลองของ Dank รูปที่แสดงคือกรณีที่ลมพัดปะทะด้านหน้า

หากพิจารณาอย่างหยาบ โดยไม่สนใจว่าสิ่งที่กำลังเคลื่อนที่หลบฝนจะเป็น คนจริงๆ กล่อง ทรงรี หรือหุ่นยนต์ R2D2 โมเดลจะอธิบายว่าความเปียกจะขึ้นกับความยาวของ "บริเวณฝน" (ให้เป็นตัวแปร l) ซึ่งจะยาวมากขึ้นถ้าคนเคลื่อนที่ช้าลง และในทางตรงข้ามมันจะสั้นลงเมื่อคนวิ่งเร็วขึ้น (l มาก เมื่อ s น้อย และ l น้อย เมื่อ s มาก ตามลำดับ) ตรงนี้จึงสามารถสรุปได้ว่า การวิ่งมีแนวโน้มที่จะทำให้เปียกน้อยลง ซึ่งสอดคล้องกับแบบจำลองของ HBHP และแนวคิดของ Jearl

ไม่เพียงเท่านี้ แบบจำลองนี้ยังได้พิสูจน์เชิงคณิตศาสตร์ว่า แนวคิดเรื่องทิศทางลมของ Matthew เกือบถูกต้อง คือผลการคำนวณจากแบบจำลองของ Dank อธิบายว่า หากฝนตกพร้อมกับมีลมพัดปะทะด้านหลังด้วยอัตราเร็ว w แล้ว "ปริมาตรฝน" จะสั้นที่สุดเมื่อคนวิ่งด้วยความเร็ว 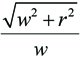 นั้นหมายความว่า ถ้าวิ่งด้วยความเร็วเท่านี้ คนจะเปียกน้อยที่สุดนั้นเอง ส่วนกรณีที่มีลมพัดปะทะด้านหน้า Matthew กล่าวถูกแล้วคือ คนควรจะวิ่งด้วยความเร็วมากที่สุดเท่าที่เขาจะทำได้จึงเปียกน้อยที่สุด

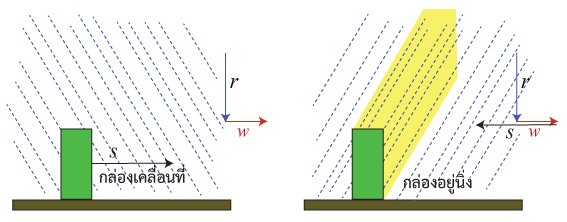
รูปแสดงกรณีที่ลมปะทะด้านหลัง หรือ ลมไล่หลัง ถ้ากล่องเคลื่อนที่เร็วพอ บริเวณฝนอาจจะเยื้องไปด้านหน้าได้

การวิ่งหลบฝนจะทำให้เปียกน้อยกว่าการเดิน

ที่ผ่านมาก็ได้พูดถึงการศีกษาปัญหา "เดินหรือวิ่งหลบฝน" ในเชิงทฤษฎี และเราก็มีแบบจำลองที่สนับสนุนว่า "รีบวิ่งหลบฝนเข้าที่ร่มอย่างที่พวกเราเคยทำกันมานั้นแหละดีแล้ว" ถึงกระนั้นก็ยังต้องมีการทดลองเพื่อยืนยันทฤษฎี การทดลองสามารถทำได้โดยลองคำนวณดูว่า การวิ่งหลบฝนจะเปียกน้อยกว่าการเดินหลบฝนเป็นค่าเท่าไร จากนั้นก็ทำการทดลองจริง หาอาสาสมัครออกไปวิ่งหรือเดิน พร้อมทั้งควบคุมตัวแปรบางอย่างเช่น ความเร็วและทิศทางของน้ำฝน และควบคุมระยะทางที่วิ่ง (แต่ไม่ควบคุมเวลา) แล้วลองวัดดูว่าคนเปียกมากน้อยเท่าไร ถ้าหากทดลองแล้วได้ผลการวัดความเปียกตรงกับที่คำนวณได้ นั้นแสดงว่าแบบจำลองนี้ถูกต้อง

ย้อนกลับไปในปี พ.ศ. 2540 นักอุตุนิยมวิทยา(อีกล่ะ?) อีกสองท่าน ชื่อ Peterson และ Wallis ได้ลองแทนค่าตัวเลขลงในการคำนวณของ HBHP เพื่อหาความแตกต่างระหว่างวิ่งหลบฝนและเดินหลบฝน (การแทนค่าได้คำนึงถึงลมพัดและการเอียงตัวขณะวิ่งด้วย แต่ไม่ขอกล่าวถึงเพราะหาแหล่งอ้างอิงไม่ได้) ผลคือหากวันใดฝนตกไม่หนักและไม่มีลมพัด ผลคำนวณบอกว่า วิ่งจะเปียกน้อยกว่าเดิน 16% ส่วนในวันที่ฝนตกหนัก มีลมพัด คนที่วิ่งไปทางเดียวกับลมแล้วเอียงตัวไปข้างหน้าเล็กน้อยจะเปียกฝนน้อยกว่าถึง 44% ตอนนี้พวกเขาได้ค่าจากการคำนวณแล้ว ถัดไปพวกเขาจะทำการทดลองเพื่อดูสิว่าตัวเลขนั้นถูกต้องมากน้อยแค่ไหน

หากผลการคำนวณถูกต้อง แสดงว่าเราควรจะวิ่งหลบฝน เว้นเสียแต่เราอยากจะเล่นน้ำฝน

การทดลองนั้นง่ายมาก (แต่ไม่รัดกุมเช่นกัน) คือ Peterson กับ Wallis จะผลัดกันออกไปวิ่ง โชคดีที่ร่างกายของทั้งสองท่านนี้คล้ายกัน สามารถใส่เสื้อและกางเกงตัวเดียวกันได้ ทั้งสองท่านจะรอวันที่ฝนตก หากวันไหนฝนตก เขาจะรีบแต่งตัวโดยใส่ชุดพลาสติกกันฝนไว้ด้านใน จากนั้นสวมเสื้อและกางเกงปกติ ไว้ด้านนอก (น้ำหนักแห้งของเสื้อและกางเกงที่ใส่ถูกชั่งและบันทึกไว้แล้ว) แล้วท่านหนึ่งจะวิ่งหรือเดินกลางฝนเป็นระยะทาง 100 เมตร ส่วนอีกท่านจะจับเวลาและคำนวณหาความเร็วของการเคลื่อนที่ ปริมาณและความเร็วของน้ำฝนก็ถูกวัดด้วยเช่นกัน เมื่อวิ่งเสร็จแล้ว เสื้อและกางเกงจะถูกชั่งน้ำหนักอีกครั้ง ผลลบของน้ำหนักที่ชั่งครั้งหลังกับน้ำหนักแห้ง คือปริมาณน้ำที่เสื้อดูดซับไว้ และนี่ก็คือความเปียก จากการทดลองซ้ำหลายครั้ง Peterson กับ Wallis จึงสรุปผลการทดลองว่า "การวิ่งหลบฝนจะเปียกน้อยกว่าการเดิน 40% คิดจากน้ำหนักของน้ำที่ถูกซับไว้ในเสื้อและกางเกง" จะเห็นว่าผลการทดลองสอดคล้องกับทฤษฎี

ทดสอบทฤษฎีด้วยการออกไปวิ่งกลางฝนจริงๆ

สรุป
ตอนนี้ (เดือน กรกฎาคม ปี พ.ศ. 2555) เข้าสู่หน้าฝนแล้ว หากมีวันใดที่ยุ่งๆ ต้องรีบออกจากบ้านแต่เช้าจนลืมหยิบร่มคู่ใจติดตัวไปด้วย หากโชคร้าย วันนั้นฝนตกลงมาพอขณะที่คุณกำลังอยู่กลางแจ้งพอดี สิ่งที่ควรทำคือวิ่งหาที่ร่มหลบฝนให้เร็วที่สุดเท่าที่จะทำได้ ถึงแม้จะมีลมพัด ก็ไม่จำเป็นต้องคำนึงว่าจะต้องวิ่งให้อัตราเท่ากับ 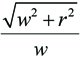เพราะจะเสียเวลาไปเปล่าๆ และถ้าหากมัวแต่ยืนคำนวณเราอาจเปียกฝนมากกว่าก็ได้ สุดท้ายนี้ หากวิ่งแล้วขอให้ระวังพื้นลื่นด้วยนะครับ





อ้างอิง
[1] "Running in the Rain"
[2] Dank HailMan, "Keeping Dry: The Mathematics of Running in the Rain", Mathemaitics Magazine (P266-P277), Oct 2009.



ที่มา : StarFall1 จากวิชาการดอทคอม