Expectation : ค่าคาดหวัง
Expectation : ค่าคาดหวัง
ในโลกเรานี้มีสถานการณ์หลายๆอย่าง ที่สามารถเกิดขึ้นได้หลายๆแบบ นำมาซึ่งจุดที่ต้องทำการตัดสินใจในเรื่องต่างๆ หากเป็นแค่สิ่งเล็กน้อยในชีวิตประจำวัน คงไม่ใช่เรื่องใหญ่นัก แต่ในทางการเงิน การเล่นหุ้น ในบริษัทธนาคาร หรือโรงงานอุตสาหกรรมที่ต้องมีการวางแผนต่างๆ รวมถึงการสร้างเครื่องมือทางวิศวกรรมของวิศวกร การตัดสินใจของนักสถิติ เมื่อต้องเจอกับ ตัวแปรสุ่ม หรือตัวแปรที่ค่าของมันวัดได้จากกระบวนการสุ่ม หรือกระบวนการที่มีความไม่แน่นอนอยู่ ถามว่าพวกเขาเหล่านั้นเมื่อต้องทำการคาดคะเนอะไรบางอย่าง พวกเขาจะทำได้อย่างไร? และใช้อะไรเป็นเครื่องมือช่วย?
คำถามเหล่านี้เอง นำมาซึ่งการศึกษาในเรื่อง ทฤษฏีความน่าจะเป็น และ สถิติศาสตร์ ซึ่งในการคาดคะเนความเป็นไปได้ของเหตุการณ์โดยรวมนั้น มีค่าๆหนึ่งที่เป็นตัวแปรสำคัญที่ถูกนำมาใช้อย่างต่อเนื่อง นั้นคือ ค่าคาดหวัง (Expectation)
ค่าคาดหวัง (Expectation) คืออะไร ? ค่าคาดหวังคือผลของความน่าจะเป็นกับผลประโยชน์ที่เราจะได้รับเมื่อสิ่งๆนั้นได้เกิดขึ้น หรือในทางสถิติศาสตร์ คือ ค่าเฉลี่ยถ่วงน้ำหนัก (weighted average) ของทุกๆค่าที่เป็นไปได้ของตัวแปรสุ่ม โดยในการคำนวณการถ่วงน้ำหนักจะใช้ค่าฟังก์ชันความหนาแน่นของความน่าจะเป็น (probability density function)สำหรับตัวแปรสุ่มต่อเนื่อง หรือใช้ค่าฟังก์ชันมวลของความน่าจะเป็น (probability mass function)
โดยค่าคาดหวังสามารถเขียนเป็นสมการง่ายๆ ดังนี้
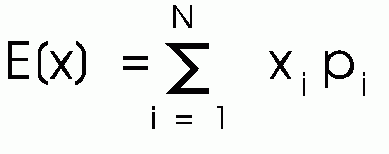
โดย E คือ ค่าคาดหวัง หรือ Expectation value
Xi คือ ตัวแปรสุ่มลำดับที่ i
Pi คือ ความน่าจะเป็นของเหตุการณ์ที่ Xiจะเกิดขึ้น
N คือจำนวนเหตุการณ์ทั้งหมด
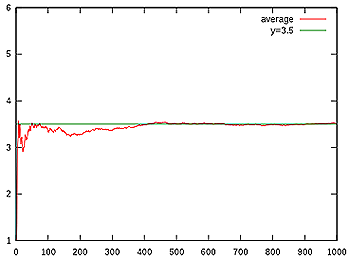
ยกตัวอย่างเช่น ถ้าเราโยนลูกเต๋าที่มี 6 หน้า แต่ละหน้ามีจำนวนตั้งแต่ 1 ถึง 6 นั้นหมายความว่าเมื่อเราทำการโยนไปเรื่อยๆ จำนวนครั้งในการโยนมากๆ โอกาสที่เราจะพบหน้าที่มีเลข 1 คือ 1/6 ,โอกาสที่จะพบหน้าที่มีเลข 2 ก็คือ 1/6 , และในทำนองคล้ายๆกันนี้ โอกาสที่เราจะพบแต่ละหน้าก็คือ 1/6 เมื่อนำมาหาค่าคาดหวัง อย่างที่ได้กล่าวไปในเบื้องต้น ค่าคาดหวังคือ ค่าเฉลี่ยน้ำหนักของตัวแปรสุ่ม ในที่นี้เราจึงจะใช้ A (Average) แทน E (Expectation) เพื่อแสดงให้เห็นถึงความเกี่ยวเนื่องกัน
ได้ว่า A = [1x1/6 + 2x1/6 + 3x1/6 + 4x1/6 + 5x1/6 + 6x1/6] = 3.5
หากเราสามารถที่จะหาค่าคาดหวังได้ มันก็จะช่วยในการวิเคราะห์ว่าการตัดสินใจนั้นๆคุ้มค่าต่อการลงทุนหรือไหม หรือคุ่มค่าต่อการเดิมพันทำหรือไม่
ตัวอย่าง Expected Value กับการลงทุน
นี่เองเป็นความลับอย่างหนึ่ง ในกระบวนการตัดสินใจของนักลงทุนหรือนักเล่นหุ้นชั้นยอดหลายๆคน เนื่องจากการที่ใครสักคนจะสามารถก้าวข้ามเข้าไปในขอบเขตของนักเล่นหุ้นที่ยอดเยี่ยมได้นั้น อย่างหนึ่งที่จะปฏิเสธไม่ได้เลยก็คือ พวกเขาจะต้องมีกระบวนการตัดสินใจที่สอดคล้องไปกับกฏของความน่าจะเป็น เพื่อที่จะสามารถสร้างผลตอบแทนที่เป็นบวก จากกลไกของค่าความคาดหวังที่จะเกิดขึ้นกับพอร์ทโฟลิโอของพวกเขา หรือพูดง่ายๆก็คือ พวกเขาต้องมีระบบหรือแนวทาง (Entry, Exit, Money management) ที่จะทำให้ผลกำไรโดยเฉลี่ยในแต่ละครั้ง (Average Win Amount) มากกว่าผลขาดทุนเฉลี่ยในแต่ละครั้ง (Average Loss Amount) ในระยะยาวออกมาให้ได้
จะเห็นได้ว่า มันไม่ใช่เรื่องที่เกียวกับหลักการเลือกหุ้นหรือหาจังหวะในการเข้าซื้อหุ้นเลย!! แต่มันเกี่ยวกับเรื่องของการสร้างผลกำไรโดยเฉลี่ยให้มากกว่าการขาดทุนโดยเฉลี่ยต่างหาก ที่จะนำไปสู่ผลกำไรที่จะเกิดขึ้นในระยะยาว มันคือผลจากขนาดของกำไรโดยเฉลี่ยในแต่ละครั้ง ไม่ใช่เรื่องของความแม่นยำ! โดยเมื่อไหร่ก็ตามที่คุณสามารถที่จะทำความเข้าใจ ว่าเรื่องนี้เกี่ยวพันกับผลตอบแทนในระยะยาวเป็นอย่างมากอย่างไรได้แล้วล่ะก็ คุณก็จะเริ่มเข้าใจว่าคุณกำลังเล่นเกมกับตัวของคุณเองในการที่จะสร้างกำไรคาดหวังในระยะยาวขึ้นมา และยิ่งคุณสามารถที่จะมองข้ามผ่านม่านหมอกที่บังตาเข้าไปได้อย่างชัดเจนมากขึ้น คุณก็จะเริ่มมองเห็นวิธีในการสร้างความได้เปรียบของคุณมากขึ้นเรื่อยๆนั่นเอง
ภาพจาก
http://www.savvysoft.com/basic.htm
https://plus.maths.org/content/maths-minute-expectation
เนื้อหาจาก
https://plus.maths.org/content/maths-minute-expectation
https://th.wikipedia.org
http://mangmaoclub.com/expected-value-mindset/



