จำนวนเฉพาะแห่งปี 2016 กับการค้นหาไร้ที่สิ้นสุด

ก่อนอื่นเลยคิดว่าหลายคนคงทราบกันดีว่า “จำนวนเฉพาะ” คืออะไร แต่สำหรับใครที่ลืมไปแล้วเรามาดูลักษณะคุณสมบัติของจำนวนเฉพาะกัน

จำนวนเฉพาะ ( Prime number ) คือ จำนวนที่มีตัวหารหรือตัวประกอบได้เพียง 2 จำนวนเท่านั้น คือตัวมันเอง และ 1

เช่น 2 , 3 , 5 , 7 , 11, 13 ,…

แต่ 1 ไม่ใช่จำนวนเฉพาะ เพราะ 1 มีตัวประกอบ เพียงตัวเดียว เท่านั้น คือ 1 นั้นเอง

และจำนวนอื่นๆนั้นถูกเรียกว่า “จำนวนประกอบ” เพราะเกิดจากการคูณกันของจำนวนเฉพาะ เช่น 28 = 2 x 2 x 7 เป็นต้น

จำนวนเฉพาะนี้มีจำนวนเป็น อนันต์ ตัว โดยเคยถูกพิสูจน์ไว้ด้วยฝีมือของนักคณิตศาสตร์ชาวกรีก ชื่อ “ยุคลิด” ในหนังสือ Elements (Book IX, Proposition 20) โดยเขาได้ใช้วิธีพิสูจน์ว่า  "มีจำนวนเฉพาะ มากกว่าจำนวนเฉพาะ[จำนวนจำกัด]ที่กำหนดให้" โดยหากจะให้อธิบายประโยคนี้ให้เข้าใจง่ายๆ สมมติว่า เรามีสมมติฐานว่าจำนวนเฉพาะนั้นมีอยู่อย่างจำกัด สมมติให้เป็น n จำนวน โดย p_n แทนจำนวนเฉพาะลำดับที่ n ยกตัวอย่างเช่น p₁ = 2 , p₂ = 3 , p₃ = 5 , p₄ = 7  เป็นต้น เราจะได้ว่าเซตของจำนวนเฉพาะ P สามารถเขียนแจกแจงได้เป็น  P = { p₁, p₂, p₃, p₄ ,…,p_n} โดย จำนวนสมาชิกของ P ก็คือจำนวนทั้งหมดของจำนวนเฉพาะที่มีอยู่อย่างจำกัด คือ N ตัวนั้นเอง

แต่เมื่อเราพิจารณา จำนวน [(p₁)x (p₂)x (p₃)x (p₄ )x … x (p_n )] + 1 พบว่า จำนวนนี้ไม่สามารถหารด้วยจำนวนเฉพาะใดๆในเซต P ได้ลงตัว หรือ ไม่ได้เกิดจากการคูณกันของจำนวนเฉพาะใดๆ ทำให้[(p₁)x (p₂)x (p₃)x (p₄ )x … x (p_n )] + 1 ไม่ใช่จำนวน ประกอบ จึงสรุปได้ว่า ยังมี [(p₁)x (p₂)x (p₃)x (p₄ )x … x (p_n )] + 1 เป็น จำนวนเฉพาะ อีกตัวที่ไม่ได้อยู่ในเซต P

โดยวิธีการคิดของยูคลิดนี้ จะพบว่า เราสามารถสร้างจำนวนเฉพาะใหม่จากการนำจำนวนเฉพาะที่มีทั้งหมดมาคูณกัน แล้วบวก 1  เพื่อไม่ให้มีจำนวนเฉพาะใดๆที่มีอยู่ก่อนหารลงตัวได้นั้นเอง แต่กระนั้นก็ตาม จำนวนเฉพาะใหม่นี้ ก็ยังไม่ใช่จำนวนเฉพาะลำดับที่ n+1  อยู่ดี ดังนั้น ก็ยังคงมีจำนวนเฉพาะมากมายที่อยู่ระหว่างค่าของ p_n และ  [(p₁)x (p₂)x (p₃)x (p₄ )x … x (p_n )] + 1

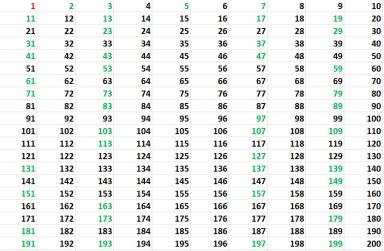
นานนับหลายทศวรรษที่เหล่านักคณิตศาสตร์มากมายพยายามค้นหาจำนวนเฉพาะใหม่ๆไปเรื่อยๆ เปรียบเสมือนการท้าทายที่ไมมีวันสิ้นสุด หากเรา พิจารณาช่วง 1 – 100 เราจะพบจำนวนเฉพาะ ทั้งหมด 25 ตัว และเมื่อขยับมาเป็นช่วง 101-200 เราพบจำนวนเฉพาะทั้งหมด 21 ตัว และช่วง 201-300 ก็พบจำนวนเฉพาะเพียง 16 ตัวเท่านั้น ซึ่งจะเห็นว่าเมื่อค่ายิ่งมากขึ้น ดูเหมือนว่าการเกิดขึ้นของจำนวนเฉพาะจะน้อยลงไปเรื่อยๆ ทำให้การหาจำนวนเฉพาะค่าที่ใหญ่ๆ  กลายเป็นเรื่อง ท้าทายอย่างมากสำหรับนักคณิตศาสตร์

แต่มีใครเคยนึกสงสัยไหมว่า “แล้วจำนวนเฉพาะที่ใหญ่ที่สุดที่ค้นพบครั้งสุดท้ายเกิดขึ้นในยุคไหน?”

...เชื่อหรือไม่ จำนวนเฉพาะที่ใหญ่ที่สุดที่เคยมีการค้นพบมา  มีตัวเลขยาวถึง 22,338,618 ตัว และ ถูกค้นพบในวันที่ 7 มกราคม ปี 2016!! นี่เอง

โดยจำนวนดังกล่าวถูกค้นพบโดย Curtis Cooper  นักคณิตศาสตร์จาก University of Central Missouri โดยเขาอาศัย เครือข่ายค้นหาจำนวนเฉพาะแมร์แซนกิมป์ (Great Internet Mersenne Prime Search : GIMPS) ซึ่งใช้ประโยชน์จากหน่วยประมวลผลของคอมพิวเตอร์อาสา  360,000 หน่วยประมวลผล ซึ่งทำการคำนวณ 450 ล้านล้านครั้งได้ใน 1 วินาที

นอกไปจากนั้นจำนวนเฉพาะนี้ยังเป็นจำนวนเฉพาะลำดับที่ 49 ของจำนวนเฉพาะแมร์แซน(ถูกนิยามเมื่อ 350 ปีก่อน) คือจำนวนเฉพาะที่อยู่ในรูป 2ⁿ – 1  โดยที่ n เป็นจำนวนเฉพาะใดๆ   โดยจำนวนเฉพาะใหม่(ที่มีค่ามากที่สุดในโลก)นี้ คือ 2^74,207,281-1

สิ่งนี้เป็นอีกสิ่งหนึ่งที่เป็นหลักฐานให้เห็นว่า คณิตศาสตร์ ยังคงเป็นศาสตร์ที่ไร้ขอบเขต รอรับการค้นพบใหม่ๆของผู้มีใจรักในคณิตศาสตร์รุ่นถัดๆไปอยู่เสมอ

เนื้อหาจาก

http://primes.utm.edu/

http://mathworld.wolfram.com/PrimeNumber.html

http://www.mersenne.org/primes/?press=M74207281

ภาพจาก

http://www.bnd.com

http://statistics.about.com