คณิตศาสตร์ใกล้ตัว : ลำดับเรขาคณิต กับ ดอกเบี้ยธนาคาร ( ตอนแรก ) !!!

     ลำดับเลขคณิต และลำดับเรขาคณิต เป็นหัวข้อที่ปัจจุบันประเทศเราได้บรรจุเป็นหลักสูตรการเรียนรู้ในระดับมัธยมศึกษาตอนปลาย หลายคนมองว่าคณิตศาสตร์เป็นเรื่องไกลตัว หรืออาจมองว่า คณิตศาสตร์ ระดับสูงนั้น ไม่เห็นสามารถใช้ได้ในชีวิตจริงแต่อย่างใด…

    “แต่ถ้าวันหนึ่ง คุณได้ไปกู้ธนาคาร 1 ล้านบาท ดอกเบี้ย 6.5%  และต้องผ่อนทุกเดือนเป็นระยะเวลา 20 ปี คุณคิดว่า จำนวนเงินจริงๆทั้งหมดที่คุณต้องจ่ายคืนเท่าไหร่ ???”

เมื่อถามคำถามนี้กับคนทั่วไปมักจะมีแนวคิดว่า ต้องจ่ายเงินต้น 1 ล้านบาท + เงินดอกเบี้ย 6.5% รวมแล้วประมาณ 1.065 ล้านบาท … แต่หากคนที่เข้าใจแก่นแท้ของลำดับเรขาคณิต เขาสามารถตอบคุณได้ทันทีว่า คุณต้องจ่ายรวมทั้งสิ้น ประมาณ 1.7 – 1.8 ล้านบาท!!!!!!  ดอกเบี้ย 6 หมื่นบาท กับดอกเบี้ย 7 แสน ดอกเบี้ยมากกว่าที่คนทั่วไปคาดเดาถึง 10 เท่า !!! คราวนี้ความจำเป็นของความรู้คณิตศาสตร์ คงกลายเป็นสิ่งที่มีประโยชน์ต่อการตัดสินใจอย่างหลีกเลี่ยงไม่ได้

ซึ่งอันที่จริงแล้ว ตัวเลข  1.7 ล้านนี้ สามารถหาได้ง่ายๆจากความรู้ในเรื่อง ลำดับเรขาคณิต ที่เราได้เรียนกันในระดับมัธยมปลายนั้นเอง

ก่อนจะไปดูว่า ธนาคารมีการนำลำดับเรขาคณิตมาใช้อย่างไร เรามาทำความเข้าใจกันก่อนว่าลำดับเรขาคณิตคืออะไรกันแน่

ลำดับเรขาคณิต ( Geometric Sequence)

     เป็นลำดับของตัวเลขที่มีอัตราส่วนร่วม (Common ratio ) คงที่ หรือ อัตราส่วนระหว่างพจน์ที่ n+1 ใดๆ กับพจน์ที่ n มีค่าคงที่เสมอ

เช่น  1 , 3 , 9 , 27 , 81 …   ข้อมูลชุดนี้เกิดจากการคูณ 3 เข้าไปเรื่อยๆ

    ดังนั้นจึงเป็นลำดับเรขาคณิต ที่มีอัตราส่วนร่วม = 3

รูปทั่วไป

   ให้  a₁  a₂  a₃  a₄  … a_n เป็นชัดข้อมูลๆ หนึ่งในชำดับเรขาคณิต โดยมีทั้งหมด n จำนวน

โดย a₁ เป็นพจน์ที่ 1 ของลำดับเรขาคณิต

และ a_n เป็นพจน์ลำดับที่ n ใดๆ ของลำดับเรขาคณิต

จากนิยามที่ว่า อัตราส่วนร่วมระหว่างพจน์ที่ติดกันมีค่าคงที่เสมอ ดังนั้น อัตราส่วนร่วม r = a_n+1 / a_n

หากเขียนแต่ละพจน์ออกมาให้ชัดเจนยิ่งขึ้น

ได้ a₁ = a₁

    a₂ = a₁r

    a₃  =  a₂r  = a₁r²

    a₄  =  a₃r  =  a₂r²  =  a₁r³

 ได้ความสัมพันธ์ว่า  a_n = a₁r^n-1

 ดังนั้น หากเขียนลำดับเรขาคณิต ในรูปของอัตราส่วนร่วม จะได้ว่า

{a₁  ,  a₂  ,  a₃  , …  a_n}    =   {a₁  ,  a₁r  ,  a₁r² ,…  a₁r^n-1 }

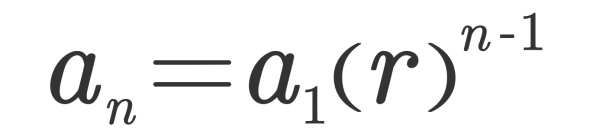
ผลอนุกรมของลำดับเรขาคณิต

   ให้ S_n คือผลรวมของลำดับเรขาคณิตทั้งหมด n พจน์

ได้ว่า s_n = a₁  +  a₂  +  a₃  + … + a_n   

            = a₁  +  a₁r  +  a₁r² +…  +a₁r^n-1   …(1)

พิจารณา rS_n = a₁r  +  a₁r²  +  a₁r³ +…  +a₁rⁿ   …(2)

แก้สมการหาค่า S_n

โดย (1) –  (2)  ได้ S_n – rS_n  =  a₁ -  a₁rⁿ

                            (1 – r)S_n = a₁(1 – rⁿ)

                             ดังนั้น S_n = a₁  +  a₁r  +  a₁r² +…  +a₁r^n-1   = a₁(1 – rⁿ)/ (1 – r)

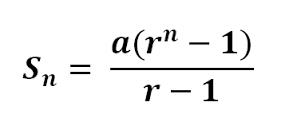
นอกจากนี้ หากค่า r < 1 จะได้ว่า ค่าของ rⁿ เมื่อ n มีค่าเจ้าใกล้ infinity ( ∞ )

เราจะได้ S_n = a₁ /(1 – r)  เมื่อ n à ∞

ความรู้เพิ่มเติม : ในบางลำดับที่หากมองดูเฉยๆ อาจไม่ทราบว่าเป็นลำดับเรขาคณิต แต่ในความเป็นจริงแล้ว ก็สามารถใช้หลักการเดียวกับการหาผลรวมของลำดับเรขาคณิตในการแก้สมการได้ เช่น

จงหาค่า A เมื่อ  A =  1 + 2²X¹ + 3²X² + 4²X³ + …   …(0) โดยที่ X < 1

พิจารณา XA =  X + 2²X² + 3²X³ + 4²X⁴ + …

ได้  A – XA = 1 + (2² – 1) X + (3² – 2²) X² + (4² – 3²) X³ +…

     (1-X)A = 1 + 3X + 5X² + 7X³ +…   …(1)

   พิจารณา X(1-X)A =  X + 3X² + 5X³ + 7X⁴ + …    …(2)

(2) – (1)    (1-X)A - X(1-X)A = 1 + 2X + 2X² + 2X³ +…

             ได้ (1-X)²A = 1 + 2X(1 + X + X² +…)

เมื่อ X < 1 ได้ (1-X)²A = 1 + 2X/(1-X)

                      A =  1/(1-X)²  + 2X/(1-X)³   เป็นต้น

คราวนี้ เมื่อเข้าใจหลักการและวิธีการคำนวณของลำดับเรขาคณิตแล้ว เราก็จะสามารถคิดคำนวณการเก็บดอกเบี้ยจริงๆ ที่เกิดขึ้นจากการกู้เงินจากธนาคารได้ โดยสามารถดูหลักการของธนาคาร ในบทความ “คณิตศาสตร์ใกล้ตัว : ลำดับเรขาคณิต กับ ดอกเบี้ยธนาคาร ( ตอนจบ )” 

เนื้อหาโดย : ธัชชัย ตระกูลเลิศยศ

ภาพจาก

http://blog.ed.gov/2012/10/five-things-to-know-about-your-student-loans/

http://alzarschool.org/viral-video-games-create-math-problems/

https://adirukmananda.wordpress.com/