ภาพที่ปรากฏบทหน้าจอคอมพิวเตอร์ที่เรามักจะเรียกกันว่าภาพกราฟิก รู้หรือไม่ว่า ในการสร้างภาพเหล่านี้ แท้จริงแล้วอุปกรณ์ที่ใช้ประกอบด้วย Hardware และ Software ที่พัฒนามาจากสมการคณิตศาสตร์    ในการสร้างภาพด้วยคอมพิวเตอร์นั้น  มีองค์ประกอบหลายอย่าง  เช่น  เครื่องคอมพิวเตอร์  อุปกรณ์รับเข้า (input device)  ที่จะรับข้อมูลเข้า  และอุปกรณ์ส่งออก (output device)  สำหรับแสดงผล โดยแสดงผลผ่านอุปกรณ์แสดงผล ได้แก่ จอภาพ และเครื่องพิมพ์

การสร้างภาพกราฟิกด้วยคอมพิวเตอร์

         มีวิธีการสร้าง 2 แบบ คือ แบบบิตแมพ (Bit Mapped) และแบบเวกเตอร์ (Vector) หรือสโตรก (Stroked)

        1.กราฟิกแบบบิตแมป มีลักษณะเป็นช่องๆ เหมือนตาราง แต่ละบิตก็คือส่วนหนึ่งของข้อมูลคอมพิวเตอร์ (ซึ่งก็คือสวิตซ์ปิดเปิดในหน่วยความจำ "1" หมายถึงเปิด และ "0" หมายถึงปิด)และสวิตซ์ปิดเปิดนี้ก็ยังหมายถึงสีดำและสีขาวอีกด้วย ดังนั้นถ้าเราเอาบิตที่แตกต่างกันในแต่ละตารางมารวมกันเข้าเราจะสามารถสร้างภาพจากจุดดำและขาว

        2.กราฟิกแบบเวกเตอร์ เป็นภาพกราฟิกที่เกิดจากการอ้างอิงความสัมพันธ์ทางคณิตศาสตร์ หรือการคำนวณ ซึ่งภาพจะมีความเป็นอิสระต่อกัน โดยแยก object ของภาพทั้งหมดออกเป็นเส้นตรง เส้นโค้ง รูปทรง เมื่อมีการขยายภาพความละเอียดของภาพจะไม่ลดลง

หลักการทำงานและการแสดงผลของภาพกราฟฟิก

          อุปกรณ์ที่ใช้แสดงผลภาพ เช่น จอคอมพิวเตอร์ หรือเครื่องพิมพ์ จะเป็นการแสดงผลภาพแบบ Raster ภาพกราฟิกแบบ Vector ที่ขยายใหญ่ขึ้น ความละเอียดของภาพจะไม่ลดลง ภาพที่เกิดบนจอคอมพิวเตอร์ เกิดจากการทำงานของโหมดสี RGB ซึ่งประกอบด้วย สีแดง สีเขียว และสีน้ำเงิน โดยใช้หลักยิงประจุไฟฟ้าให้เกิดการเปล่งแสงของสีทั้ง 3 สีมาผสมกัน ทำให้เกิดเป็นจุดสีสี่เหลี่ยมเล็ก ๆ ที่เรียกว่า พิกเซล (Pixel) ซึ่งมาจากคำว่า Picture กับ Element โดยพิกเซลจะมีหลากหลายสี เมื่อนำมาวางต่อกันจะเกิดเป็นรูปภาพ ซึ่งภาพที่ใช้กับเครื่องคอมพิวเตอร์มี 2 ประเภท คือ แบบ Raster กับ Vector       โดยที่มี Resolution คือ  จำนวนจุดภาพทั้งหมด ที่ปรากกฏบนอุปกรณ์แสดงผล

          ระบบโคออร์ดิเนต (Coordinate system)  เป็นระบบการวาดและแสดงผลภาพผ่านจอภาพที่สามารถแสดง object ต่าง ๆ ใน 2 และ 3 มิติ  สำหรับบทความนี้จะนำเสนอมุมมอง 2 มิติเพียงเท่านั้น โดยระบบระบบโคออร์ดิเนตที่เราคุ้นเคยที่สุดและเป็นมาตรฐานที่สุดก็คือระบบโคออร์ดิเนตคาร์ทีเชียน (Cartesian) ซึ่งระบุโดยคู่พิกัด (x, y) ตามแนวนอนและแนวตั้งตามลำดับ โดยมีจุดกำเนิด (origin) ที่ (0, 0) ค่าของแกน x จะเพิ่มขึ้นจากซ้ายไปขวา ส่วนค่าของแกน y จะเพิ่มขึ้นจากล่างขึ้นบน แกนทั้งสอง (x และ y) จะตั้งฉากซึ่งกันและกันและรวมกันเรียกว่า xy-plane หรือระนาบ xy

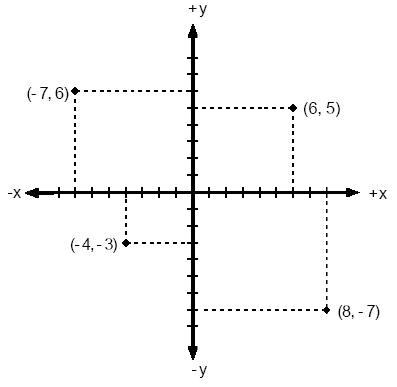
ภาพที่ 1 : ระบบโคออร์ดิเนตคาร์ทีเซียน 2 มิติ
ที่มา : www.batk.mju.ac.th/goverment/20111119104835_2011_batk/10585.ppt

ระบบพิกัดโลก(world coordinate system)

         เป็นระบบที่ใช้อธิบายตำแหน่งของภาพวัตถุในธรรมชาติระบบนี้จะไม่ขึ้นกับขนาดพิกัดของจอภาพ ดังนั้นช่วงตัวเลขที่ใช้จะเป็นเท่าใดก็ได้จะมีค่าเป็นบวกหรือลบหรือแม้แต่เลขทศนิยมก็ได้เช่นกัน

Window

         ในบางครั้งภาพสมบูรณ์ของวัตถุที่ใช้ระบบพิกัดโลกอธิบายตำแหน่งนั้นมีขนาดใหญ่และซับซ้อนมาก และผู้ใช้ต้องการแสดงภาพเพียงบางส่วนของวัตถุเท่านั้นความสามารถในการแสดงภาพเพียงบางส่วนของภาพวัตถุภายในบริเวณสี่เหลี่ยมที่กำหนดไว้ เราเรียกว่า “การทำช่องหน้าต่าง”(windowing) กรอบสี่เหลี่ยมที่ใช้แสดงภาพนั้นเรียกว่า “หน้าต่าง”(window)

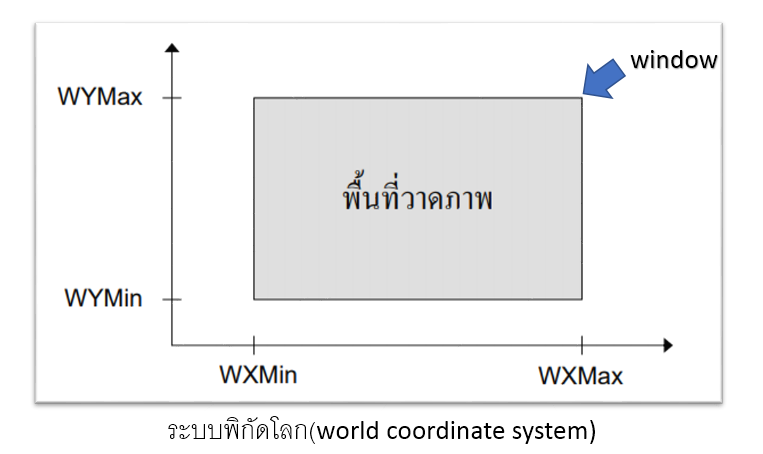ภาพที่ 2 : การแสดงผลผ่านจออุปกรณ์คอมพิวเตอร์ ส่วนต่าง ๆ ของภาพจะถูกนำมาแสดงบนจอภาพได้
โดยการนำ window ไปวางไว้ตรงส่วนนั้นของภาพในระบบพิกัดโลก
ที่มา : http://personal.sut.ac.th/

          ในการเขียนโปรแกรมให้เกิดการแสดงผลผ่านจออุปกรณ์คอมพิวเตอร์ ส่วนต่าง ๆ ของภาพจะถูกนำมาแสดงบนจอภาพได้โดยการนำ window ไปวางไว้ตรงส่วนนั้นของภาพในระบบพิกัดโลก การปรับเปลี่ยน ขนาดของหน้าต่างจะทำให้เกิด การย่อ การขยาย หรือการบิดเบี้ยวของภาพ ซึ่งอยู่ในหน้าต่างได้เราต้องแปลง

Viewport

          Viewport หรือช่องแสดงภาพคือ เนื้อที่สี่เหลี่ยมบนจอภาพซึ่งมีส่วนของภาพใน window ที่ต้องการแสดงผล viewport มีประโยชน์ในเรื่องการแสดงส่วนของภาพ หลาย ๆ ส่วนบนจอภาพเดียวกัน โดยให้เห็นทุกส่วนพร้อม ๆ กัน สามารถทำได้โดยแบ่งจอภาพเป็นส่วน ๆ แต่ละส่วนของจอภาพนั้น แสดงแต่ละส่วนของภาพที่ต้องการ

Normalization

          คือการแปลง World Coordinate ไปเป็น Normalized หรือ Device Coordinates เพื่อที่จะนำไปแสดงที่อุปกรณ์แสดงผลต่อไป

          ความสัมพันธ์ระหว่าง World และ Device coordinates เขียนได้ดังนี้

               (Xw-WXmin)/(WXMax-WXMin) = (Xd - DXMin)/(DXMax-DXMin)

                                                            Xd = Xw*A +B

               โดยที่ A = (DXmax-DXmin)/(WXmax-WXmin)

                         B = - WXmin (DXmax-DXmin)/(WXmax-WXmin) + DXmin

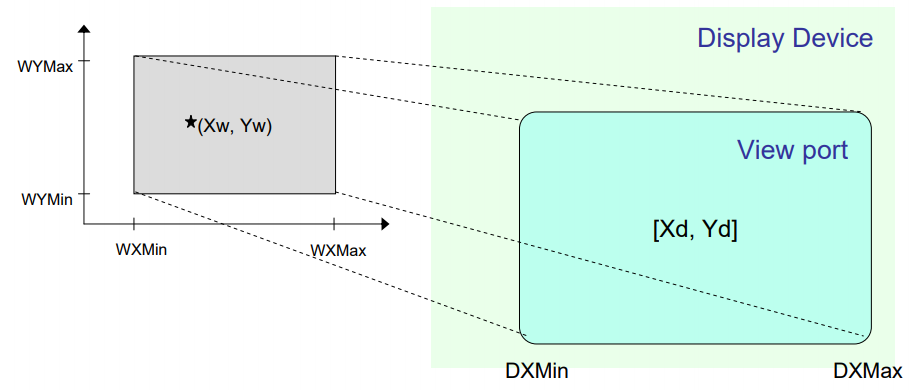ภาพที่ 3 : การแปลง World Coordinate ไปเป็น Normalized หรือ Device Coordinates เพื่อที่จะนำไปแสดงที่อุปกรณ์แสดงผล
ที่มา : http://personal.sut.ac.th/

การวาดเส้นตรงบนจอภาพสามารถแสดงไดโดยใช้สมการเสนตรง

เส้นตรง (Line) สมการในการคำนวณหาเส้นตรงคือ Y = mX + b โดยที่ m และ b คือ ความชัน และจุดตัดแกน  y ของเส้นตรง ตามลําดับ

m = (Y2 – Y1) / (X2 – X1) และ b คือจุดตัดของเส้นตรงบนแกน Y หาได้จากb = Y1 – mX1

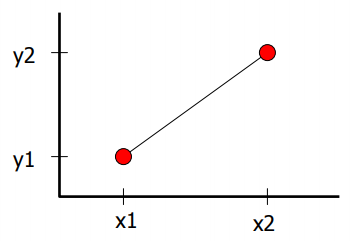
ภาพที่ 4 : การวาดเส้นตรงโดยใช้สมการทางคณิคศาสตร์
ที่มา : http://personal.sut.ac.th/

แหล่งที่มา
เอกสารประกอบการสอนรายวิชา สถาปัตยกรรมคอมพิวเตอร์ (Computer Architecture).สืบค้นเมื่อวันที่ 7 สิงหาคม 2560.จาก http://www.batk.mju.ac.th/goverment/20111119104835_2011_batk/10585.ppt.

อ. ดร. ปรเมศวร์ ห่อแก้ว.เอกสารประกอบการสอนรายวิชา Computer Graphics.สืบค้นเมื่อวันที่ 7 สิงหาคม 2560.จาก http://personal.sut.ac.th/paramate/files/compgraph/lecture01.pdf. 

อ. ดร. ปรเมศวร์ ห่อแก้ว.เอกสารประกอบการสอนรายวิชา Computer Graphics.สืบค้นเมื่อวันที่ 7 สิงหาคม 2560.จาก http://person al.sut.ac.th/paramate/files/compgraph/lecture02.pdf.

ความรู้เกี่ยวกับกราฟิก.สืบค้นเมื่อวันที่ 7 สิงหาคม 2560.จาก http://graphic222324detials.blogspot.com/2013/10/computer-graphic.html. 

งานนำเสนอเรื่อง: "Computer Graphics เรขาคณิต 2 มิติ 1.สืบค้นเมื่อวันที่ 7 สิงหาคม 2560.จาก http://slideplayer.in.th/slide/2215375/.