ความมหัศจรรย์ของเลขฟีโบนักชี ตอนที่ 2 : 1.618 สัดส่วนมหัศจรรย์แห่งธรรมชาติ
จากบทความครั้งที่แล้ว เรื่อง ความมหัศจรรย์ของเลขฟีโบนักชี ตอนที่ 1 : รู้จักลำดับเลขฟีโบนักชี
เราได้เห็นความมหัศจรรย์ของเลขฟีโบนักชี 1 1 2 3 5 8 13 21 34 55 …
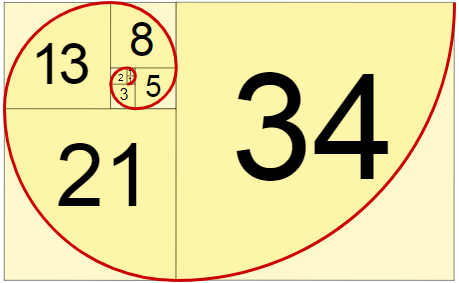
ภาพที่ 1 ตัวเลขลำดับ Fibonacci numbers
ที่มา https://www.mathsisfun.com
ความสอดคล้องและเกี่ยวพันกันกับตัวเลขค่าหนึ่งที่เรียกว่า ฟี Phi (φ) หรือค่าตัวเลขคงที่ 1.618 ด้วยเหตุที่ว่า ถ้าเอาตัวเลขฟีโบนักชีตัวหนึ่งมาหารด้วยตัวเลขฟิโบนักชีลำดับก่อนหน้าจะได้ผลหารใกล้เคียงกับค่า Phi หรือ 1.618 เสมอ หลายคนก็คงอาจสงสัย หรืออยากรู้ต่อไปว่า จำนวน Phi หรือ 1.618 ในทางคณิตศาสตร์ คืออะไร มีความสำคัญอย่างไรบ้าง
ความสัมพันธ์ของกับการนำเลขฟีโบนักชีมาสร้างเป็นสี่เหลี่ยมเพื่อหาค่าพื้นที่ดังภาพ ทำให้เกิดความสัมพันธ์หนึ่ง ที่เรียกว่า อัตราส่วนทอง
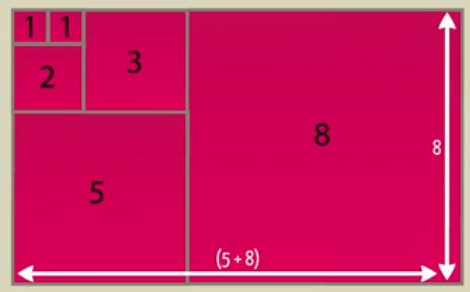
ภาพที่ 2 การจัดเรียงสี่เหลี่ยมจัตุรัสที่มีความยาวด้านเท่ากับจำนวนฟีโบนักชี
ที่มา https://www.ted.com/talks/arthur_benjamin_the_magic_of_fibonacci_numbers?language=th#t-270607
จะพบได้ว่า พื้นที่ = 12 + 12 + 22 + 32 + 52 + 82 = 8 X 13 และเมื่อนำ 13 หารด้วย 8 จะมีค่าเข้าใกล้ 1.618 เช่นเดียวกัน เมื่อนำขนาดของพื้นที่ ที่เกิดจากจำนวนฟีโบนักชียกกำลังสอง มาสร้างเป็นสี่เหลี่ยมพื้นผ้า จะได้ค่าประมาณดังนี้
13 X 21 21 หารด้วย 13 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.618
21 X 34 34 หารด้วย 21 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.618
34 X 55 55 หารด้วย 34 จะได้ค่าประมาณใกล้เคียงเท่ากับ 1.618
เมื่อลองสังเกตเลขสองจำนวนที่เป็นขนาดความยาวด้านข้างที่เกิดจากการคำนวณขนาดของพื้นที่จากภาพสี่เหลี่ยมผืนผ้าดังกล่าว โดยให้เป็นด้าน a และ ด้าน b และ a>b สัดส่วนทองคำ (golden section) คือส่วนของเส้นที่ถูกแบ่งตรงตำแหน่งที่ก่อให้เกิด "อัตราส่วนทอง (golden ratio)" กล่าวคือ อัตราส่วนของความยาวรวม a + b ต่อความยาวส่วนที่ยาว a มีค่าเท่ากับความยาวส่วนที่ยาว a ต่อความยาวของส่วนที่สั้น b โดยมีค่าประมาณเข้าใกล้ค่า (φ)
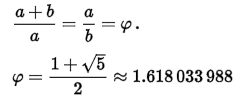
ภาพที่ 3 อัตราส่วนระหว่างค่าของลำดับ fibonacci 2 ค่า
ที่มา https://th.wikipedia.org/wiki
สัดส่วนสี่เหลี่ยมผืนผ้าทองคำ หรือ อัตราส่วนทอง (golden ratio) ที่เราสามารถพบได้ในธรรมชาติ ทั้งสิ่งมีชีวิต และไม่มีชีวิต อาทิเช่น
มหาวิหารพาร์เธนอน (Parthenon)
เป็นที่น่าสนใจที่พบว่า สถาปัตยกรรมที่เรารู้จักกันดีอย่างมหาวิหารพาร์เธนอน (Parthenon) มีขนาดกว้าง 30.9 เมตร ยาว 69.5 เมตร (101.4 × 228.0 ฟุต) เมื่อนำขนาดของวิหารนี้มาคำนวณเป็นอัตราส่วน จะพบว่าเป็นอัตราส่วนทองคำ

ภาพที่ 4 มหาวิหารพาร์เธนอน (Parthenon)
ที่มา https://th.wikipedia.org/wiki
พีระมิด
สถาปัตยกรรมระดับโลกอย่างพีระมิดของอียิปต์ ที่อัตราส่วนระหว่างความสูงเอียงของพีระมิดต่อความยาวครึ่งฐานของพีระมิดเป็นอัตราส่วนทอง

ภาพที่ 5 มหาวิหารพาร์เธนอน (Parthenon)
ที่มา http://jwilson.coe.uga.edu/emat6680/parveen/ancient_egypt.htm
เกลียวในเปลือกของหอยนอติลุสหรือหอยงวงช้าง
อัตราส่วนระหว่างเส้นผ่านศูนย์กลางของเกลียวรอบเปลือกหอยนอติลุส

ภาพที่ 6 เกลียวในเปลือกของหอยนอติลุส
ที่มา http://www.reurnthai.com/index.php?topic=6355.75
เมล็ดดอกทานตะวัน
การจัดเรียงตัวเป็นเกลียว แต่ละเกลียวจะตรงกับเลขฟีโบนักชี จำนวนเมล็ดที่อยู่ในเกลียว ที่หมุนตามเข็มนาฬิกามีอัตราส่วนเท่ากับอัตราส่วนทองคำ “phi”

ภาพที่ 7 การจัดเรียงตัวเป็นเกลียวของเมล็ดดอกทานตะวัน
ที่มา http://cdipthailand.com/media/kunena/attachments/760/golden2.jpg
กายวิภาคของมนุษย์
อัตราส่วนของสัดส่วนโครงสร้างร่างกายของมนุษย์ วัดระยะจากหัวถึงพื้นหารด้วยระยะจากสะดือถึงพื้น ระยะจากไหล่ถึงปลายนิ้วมือหารด้วยระยะจากข้อศอกถึงปลายนิ้วมือ หรือระยะจากสะโพกถึงพื้นหารด้วยระยะจากหัวเข่าถึงพื้น
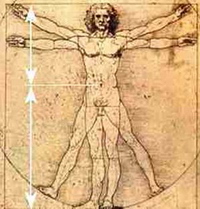
ภาพที่ 8 การจัดเรียงตัวเป็นเกลียวของเมล็ดดอกทานตะวัน
ที่มา http://www.mwit.ac.th/~dainu/story/story10.htm
โมนาลิซ่า(Mona Lisa)
สี่เหลี่ยมผืนผ้าทองคำที่ปรากฏอยู่บนใบหน้าและส่วนต่างๆของ โมนาลิซา ซึ่งเป็นภาพวาดที่มีชื่อเสียงมากที่สุดรูปหนึ่งของโลก ที่วาดขึ้นโดย เลโอนาร์โด ดา วินชี

ภาพที่ 9 โมนาลิซ่า(Mona Lisa)
ที่มา https://d3ii8mlq8d5cne.cloudfront.net/blog/monalisa.jpg
ที่กล่าวมาทั้งหมดนี้ก็เป็นเพียงส่วนหนึ่งของความงดงามอย่างน่าประหลาดของธรรมชาติ กับความสัมพันธ์ในสัดส่วนทางคณิตศาสตร์
แหล่งที่มา
หล่อสวยด้วยคณิตศาสตร์. สืบค้นเมื่อ 23 สิงหาคม 2560, จาก
http://www.mwit.ac.th/~dainu/story/story10.htm
อัตราส่วนทอง. สืบค้นเมื่อ 23 สิงหาคม 2560, จาก
https://th.wikipedia.org/wiki/



