1.หลักการนับ

          การนับอย่างเป็นระบบจะทำให้สามารถอธิบายปัญหาการนับได้ด้วยหลักการทางคณิตศาสตร์ผ่านแบบรูป ช่วยให้การแจงนับสิ่งของต่าง ๆที่มีขนาดใหญ่ไม่ใช่อุปสรรคอีกต่อไป และทำให้เกิดการแจงนับที่มีความรัดกุมสำหรับปัญหาการนับที่มีความซับซ้อน กฎพื้นฐานการนับเกิดจากเทคนิคการวิเคราะห์การทำงานในการนับ 2 วิธีคือ 1) การนับจำนวนวิธีการทำงานแบบเป็นขั้นตอน กล่าวคือเมื่อทำงานในขั้นตอนที่แรกเสร็จจะต้องทำงานต่อในขั้นตอนถัดมา การนับการทำงานแบบขั้นตอนต่อเนื่องนี้สอดคล้องกับกฎการคูณ และ 2) การนับจำนวนวิธีการทำงานแบบแบ่งกรณี โดยที่รูปแบบของวัตถุในกรณีแรกจะต้องไม่ซ้ำกับรูปแบบของวัตถุในกรณีที่สอง การนับแบบแยกกรณีนี้จะสอดคล้องกับกฎการบวก ดังนั้นการวิเคราะห์แบบรูปและวิธีการนับจึงเป็นสิ่งสำคัญช่วยให้การแก้ปัญหาเรื่องการนับมีความรัดกุมถูกต้อง

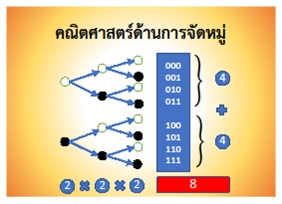
 ภาพกฎการคูณและกฎการบวก

• กฎการบวกและกฎการคูณ

      กำหนดเซตสองเซต A = {1,2,3} และ B = {4,5,6} ต้องการสร้างเลข 2 หลักโดยที่หลักสิบเป็นสมาชิกของเซต A และหลักหน่วยเป็นสมาชิกของเซต B เราจะทำการวิเคราะห์การสร้างจำนวนสองหลัก 2 แบบคือ

      แบบที่ 1 เราแบ่งการสร้างออกเป็นกรณีโดยเริ่มที่หลักสิบจะแบ่งได้ 3 กรณีคือ

            กรณีที่ 1 หลักสิบเป็นเลข 1 และหลักหน่วยอยู่ในเซต B จะได้ {14,15,16} มีจำนวน 3 แบบ

            กรณีที่ 2 หลักสิบเป็นเลข 2 และหลักหน่วยอยู่ในเซต B จะได้ {24,25,26} มีจำนวน 3 แบบ

            กรณีที่ 3 หลักสิบเป็นเลข 3 และหลักหน่วยอยู่ในเซต B จะได้ {34,35,36} มีจำนวน 3 แบบ

             รูปแบบทั้งหมดจะเป็นไปตามกฎการบวกเท่ากับ 3 + 3 + 3 = 9 แบบ

      แบบที่ 2 เราแบ่งการสร้างจำนวนสองหลักออกเป็น 2 ขั้นตอน

           ขั้นตอนที่ 1 เลือกเลขหลักสิบในเซต A ได้ 3 แบบ

           ขั้นตอนที่ 2 เลือกเลขหลักหน่วยในเซต B ได้ 3 แบบ

            รูปแบบทั้งหมดจะเป็นไปตามกฎการคูณเท่ากับ 3 x 3 = 9 แบบ

      จากปัญหาการสร้างเลขสองหลักข้างต้นเราสรุปกฎการนับได้ดังนี้

กฎการคูณ สมมติให้การทำงานมีลำดับขั้นตอน S1 และ S2 โดยที่การทำงาน S1 สามารถทำได้ m วิธีและการทำงาน S2 สามารถทำได้ n วิธีแล้วจำนวนการทำงาน S1 แล้วทำงาน S2 จะมีวิธีทำงานได้ทั้งหมด m x n วิธี

       การวางนัยยะทั่วไปกฎการคูณ สมมติให้เรามีลำดับขั้นการทำงาน k ขั้นตอนโดยที่

       ขั้นตอนที่ 1 มีจำนวนวิธีการทำงาน w1 วิธี

       ขั้นตอนที่ 2 มีจำนวนวิธีการทำงาน w2 วิธี

        …………………………………………

       ขั้นตอนที่ k มีจำนวนวิธีการทำงาน wk วิธี

      จำนวนวิธีการทำงานทั้งหมดเท่ากับ w1 x w2 x … x wk วิธี

ตัวอย่างที่ 1 จงหาจำนวนวิธีในการทอดลูกเต๋าหนึ่งลูกแล้วโยนเหรียญหนึ่งเหรียญ

วิธีทำ แบ่งการทำงานออกเป็น 2 ขั้นตอน

      ขั้นตอนที่ 1 ทอดลูกเต๋าหนึ่งลูกได้ผลลัพธ์ {1,2,3,4,5,6}      6 แบบ

      ขั้นตอนที่ 2 โยนเหรียญหนึ่งเหรียญได้ผลลัพธ์ {หัว,ก้อย} 2 แบบ

       จำนวนวิธีทั้งหมดเท่ากับ 6 x 2 = 12

ตัวอย่างที่ 2 จงหาวิธีสร้างจำนวนเต็มคู่ 3 หลักจากเลข 0,1,2,…,9

วิธีทำ เนื่องจากจำนวนคู่จะต้องมีหลักหน่วยเป็นเลข {0,2,4,6,8} และเลขสามหลักค่าในหลักร้อยจะต้องไม่เป็น 0 จึงแบ่งขั้นตอนการสร้างออกเป็น 3 ขั้นตอน

      ขั้นตอนที่ 1 เลือกเลขหลักหน่วยจาก {0,2,4,6,8} ได้  5 แบบ

      ขั้นตอนที่ 2 เลือกเลขหลักสิบจาก {0,1,2,…,9} ได้             10 แบบ

      ขั้นตอนที่ 3 เลือกเลขหลักสิบจาก {1,2,3,…,9} ได้               9 แบบ

      จำนวนเลขคู่สามหลักมีทั้งหมด 5 x 10 x 9 = 450 จำนวน

        กฎการบวก สมมติให้การทำงานสามารถแบ่งกรณีได้สองกรณีคือ C1 และ C2 โดยที่รูปแบบวิธีการทำงานในกรณี C1 และ กรณี C2 แตกต่างกันทั้งหมด ถ้ากรณี C1 มีรูปแบบการทำงาน m วิธีและกรณี C2 มีวิธีการทำงาน n วิธีแล้วการทำงานอาจมีรูปแบบในกรณี C1 หรือกรณี C2 จะมีวิธีการทำงานทั้งหมด m + n วิธี

       การวางนัยยะทั่วไปกฎการบวก สมมติว่าวิธีการทำงานทั้งหมดแยกได้เป็น k กรณีที่มีรูปแบบแตกต่างกันโดยที่

       กรณีที่ 1 มีจำนวนวิธีการทำงาน w1 วิธี

       กรณีที่ 2 มีจำนวนวิธีการทำงาน w2 วิธี

       …………………………………………

       กรณีที่ k มีจำนวนวิธีการทำงาน wk วิธี

       จำนวนวิธีการทำงานทั้งหมดเท่ากับ w1 + w2 + … + wk วิธี

ตัวอย่างที่ 3 จงหาจำนวนเลขสองหลักที่ 9 หารลงตัว

วิธีทำ เลขสองหลัก ab จะถูก 9 หารลงตัวถ้า 9 หาร a + b ได้ลงตัว เมื่อพิจารณา a + b น้อยสุดคือ 0 มากที่สุดคือ 18 ดังนั้นเราสามารถแบ่งเป็นกรณีได้ดังนี้

         กรณีที่ 1 a + b = 9 ได้แก่ {18,27,36,45,54,63,72,81,90}  มี  9 จำนวน

         กรณีที่ 2 a + b = 18 ได้แก่ {99}  มี 1 จำนวน

         จำนวนเลขสองหลักที่ 9 หารลงตัวมี 9 + 1 = 10 จำนวน

ตัวอย่างที่ 4 กำหนดให้เซต A = {1,2} จงหาจำนวนสับเซตของเซต A

วิธีทำ สับเซตที่มีขนาดเล็กที่สุดคือเซตว่างซึ่งมีสมาชิก 0 ตัวและสับเซตที่มีขนาดใหญ่ที่สุดคือเซต A ซึ่งมีสมาชิก 2 ตัวดังนั้นเราแบ่งกรณีของสับเซตทั้งหมดได้ดังนี้

         กรณีที่ 1 สับเซตที่มีสมาชิก 0 ตัว { } มี          1 เซต

         กรณีที่ 2 สับเซตที่มีสมาชิก 1 ตัว {1}, {2} มี   2 เซต

         กรณีที่ 3 สับเซตที่มีสมาชิก 2 ตัว {1,2} มี      1 เซต

        จำนวนสับเซตทั้งหมดของเซต A เท่ากับ 1+2+1 = 4 เซต

• ปัญหาการนับ

          พิจารณาการหยิบบอลจากกล่องที่มีลูกบอลสีแดงจำนวน 2 ลูกและลูกบอลสีขาว 2 ลูก ถ้าลูกบอลทั้ง 4 ลูกแตกต่างกันทั้งหมดเขียนแทนได้ด้วย {r1,r2,w1,w2} พิจารณาปัญหาต่อไปนี้

         ปัญหา P1: สนใจการเลือกลูกบอล 2 ลูกจากลูกบอล 4 ลูกที่แตกต่างกัน

         { {r1,r2}, {r1,w1}, {r1,w2}, {r2,w1}, {r2,w2}, {w1,w2} } จะได้จำนวน 6 แบบ

         ปัญหา P2: สนใจการเรียงลูกบอล 2 ลูกจากลูกบอล 4 ลูกที่แตกต่างกัน

         { r1r2, r1w1, r1w2, r2w1, r2w2, w1w2, r2r1, w1r1, w2r1, w1r2, w2r2, w2w1 } จะได้จำนวน 12 แบบ

         พิจารณาการหยิบบอลจากกล่องที่มีลูกบอลสีแดงจำนวน 2 ลูกและลูกบอลสีขาว 2 ลูก โดยที่ลูกบอลแต่ละสีไม่แตกต่างกัน {2r,2w}

          ปัญหา P3 สนใจการเลือกลูกบอล 2 ลูกจากลูกบอล 4 ลูกที่แต่ละสีไม่แตกต่างกัน

          { {2r}, {r,w}, {2w} } จะได้จำนวน 3 แบบ

          ปัญหา P4 สนใจการเรียงลูกบอล 2 ลูกจากลูกบอล 4 ลูกที่แต่ละสีไม่แตกต่างกัน

           { rr, rw, wr, ww } จะได้จำนวน 4 แบบ

           จากปัญหาทั้งสี่เราจึงต้องวิเคราะห์ปัญหาในการนับว่าปัญหานั้นสนใจอันดับหรือไม่ และสิ่งที่ถูกนับนั้นมีความแตกต่างกันหรือไม่ จากตารางที่ 1 นำมาซึ่งหลักการการจัดเรียงสิ่งของที่แตกต่างกัน การจัดเรียงสิ่งของที่ซ้ำกัน และการจัดหมู่

ตารางที่ 1 หลักการวิเคราะห์ปัญหาการนับ

แหล่งที่มา

Faticoni G.T. (2013). Combinatorics an introduction. John Wiley & Sons, Canada.

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

Harnett D.L. (1998). Data, Statistic, and Decision model with excel. John Wiley & Sons, USA.

วีระ ยุคุณธร (2016) เอกสารประกอบการสอนวิชาคณิตศาสตร์เต็มหน่วย มหาวิทยาลัยราชภัฏกาญจนบุรี.

 การจัดเรียงเชิงเส้น

ปัญหาการจัดเรียงเชิงเส้นของสิ่งของที่แตกต่างกันทั้งหมด

       สมมติให้มีสิ่งของที่แตกต่างกัน n สิ่งนำมาจัดเรียง p ตำแหน่งมีวิธีการทำงานดังนี้

       ขั้นตอนที่ 1 ในตำแหน่งที่ 1 นำสิ่งของมาวางได้ n แบบ

       ขั้นตอนที่ 2 ในตำแหน่งที่ 2 นำสิ่งของมาวางได้ n - 1 แบบ

       ขั้นตอนที่ 3 ในตำแหน่งที่ 3 นำสิ่งของมาวางได้ n - 2 แบบ

        ………………………………………………..

       ขั้นตอนที่ r ในตำแหน่งที่ p นำสิ่งของมาวางได้ n - (p - 1) = n – p + 1 แบบ

        จำนวนวิธีทั้งหมดเท่ากับ n(n - 1)(n - 2)…(n – p + 1) วิธี เราต้องการเขียนจำนวนข้างต้นในรูปแฟคทอเรียลจึงคูณด้วย (n - p)! / (n - p)! จะได้ n! / (n - p)! เขียนแทนจำนวนวิธีการจัดเรียงสิ่งของที่แตกต่างกัน n สิ่งนำมาจัดเรียง p ตำแหน่งด้วย

        P(n,p) = n! / (n-p)! = n(n - 1)(n - 2)…(n – p + 1)

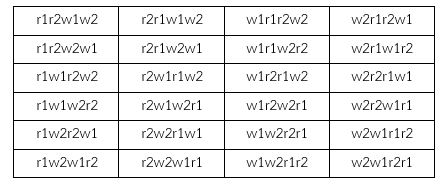
ตัวอย่างที่ 5 ถ้าเราปรับปัญหา P2 เปลี่ยนเป็นสนใจการเรียงลูกบอล 4 ลูก จะได้

        P(4,4) = 4! / (4-4)! = 4! / 0! = 4! = 4 x 3 x 2 x 1 = 24

         แจกแจงรูปแบบได้ดังตารางที่ 2

ตารางที่ 2 รูปการจัดเรียงลูกบอล {r1,r2,w1,w2}

       ตัวอย่างที่ 6 มีเก้าอี้ 9 ตัวตั้งในแนวเส้นตรงมีผู้ชาย 10 คนและผู้หญิง 8 คนจงหาวิธีการนั่งสลับระหว่างผู้ชายและผู้หญิง

       วิธีทำ เราแบ่งปัญหาเป็น 2 กรณีคือ

          กรณีที่ 1 มีผู้ชาย 5 คนและผู้หญิง 4 จะได้ P(10,5) x P(8,4)

          กรณีที่ 2 มีผู้ชาย 4 คนและผู้หญิง 5 จะได้ P(10,4) x P(8,5)

          จะได้รูปแบบในการนั่งทั้งหมด  P(10,5) x P(8,4) + P(10,4) x P(8,5) = (5/12) x P(10,5) x P(8,3)

• ปัญหาการจัดเรียงเชิงเส้นของสิ่งของที่ไม่แตกต่างกันทั้งหมด

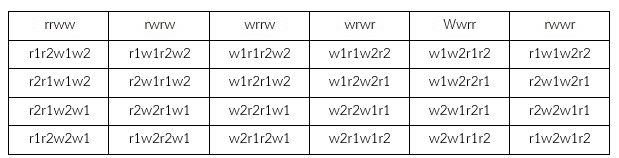
          จากตัวอย่างที่ 5 ถ้าเรามาจัดหมวดหมู่ใหม่โดยพิจารณาการจัดเรียง rrww := { r², w² } จะได้ 6 แบบซึ่งเป็นการจัดเรียงของซ้ำ สังเกตว่าหากเปลี่ยนของซ้ำให้เป็นสิ่งของที่แตกต่างกันจะทำให้ได้รูปแบบการจัดเรียงสิ่งของที่แตกต่างกันทั้งหมด ในที่นี้ เราจะพบว่า r ซ้ำ 2 และ w ซ้ำ 2 หากเราเรียงสับเปลี่ยน r ได้ 2! และ เรียงสับเปลี่ยน w ได้ 2! จะพบว่าได้รูปแบบการจัดเรียงของที่แตกต่างกัน 4 ชิ้นนั้นคือ การจัดเรียงสิ่งของที่แตกต่างกัน 4 ชิ้น  = การจัดเรียงสิ่งของที่ซ้ำกัน x การเรียงสับเปลี่ยน r x การเรียงสับเปลี่ยน w นั้นคือ 4! = การจัดเรียงของซ้ำ x 2! x 2! ดังนั้น การจัดเรียงของซ้ำ = 4! / (2! x 2!) = 6 แบบ ดังตารางที่ 3

ตารางที่ 3 ความสัมพันธ์การจัดเรียงของซ้ำ rrww และของที่แตกต่างกันทั้งหมด r1r2w1w2

         หากเราทำการวางนัยยะสมมติให้มีสิ่งของ n สิ่ง n1,n2,...,nn โดยที่แต่ละชิ้นซ้ำ k1,k2,…,kn นั้นเขียนแทนด้วยเซต {n1^k1, n2^k2,…,nn^kn} จะได้รูปแบบการจัดเรียงของเท่ากับ n! / [k1! x k2! x … x kn!]

ตัวอย่างที่ 7 จงหาวิธีการจัดเรียงคำว่า MISSISSIPPI โดยไม่สนใจความหมาย

วิธีทำ เขียน MISSISSIPPI ในรูป M¹I⁴S⁴P² จะได้วิธีการจัดเรียงทั้งหมดเท่ากับ 11! / [1! x 4! x 4! x 2!]

ตัวอย่างที่ 8 ระบบอัตโนมัติระบบหนึ่งใช้เซนเซอร์จำนวน 10 ตัว จงหาว่าสถานะที่มีการทำงานของเซนเซอร์เพียง 4 ตัวเป็นไปได้ทั้งหมดกี่สถานะ

วิธีทำ กำหนดให้สถานะที่เซนเซอร์ทำงาน = 1 และไม่ทำงาน = 0 เนื่องจากมีเซนเซอร์ทำงาน 4 ตัวและไม่ทำงาน 6 ตัวจะได้ 1⁴0⁶  สถานะที่เป็นไปได้เท่ากับ 10! / [4! x 6!]

แหล่งที่มา

Faticoni G.T. (2013). Combinatorics an introduction. John Wiley & Sons, Canada.

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

Harnett D.L. (1998). Data, Statistic, and Decision model with excel. John Wiley & Sons, USA.

วีระ ยุคุณธร (2016) เอกสารประกอบการสอนวิชาคณิตศาสตร์เต็มหน่วย มหาวิทยาลัยราชภัฏกาญจนบุรี.

 การจัดเรียงเชิงวงกลม

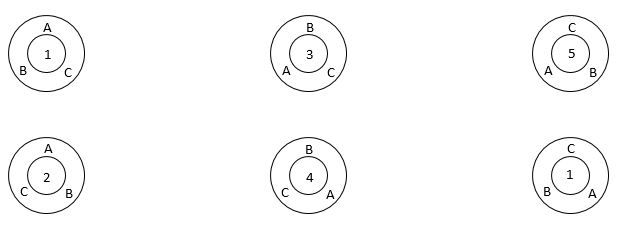
       พิจารณาเซต { A,B,C } ถ้าเราทำการจัดเรียงเชิงเส้นจะได้ 6 แบบคือ ABC ACB BAC BCA CAB และ CBA แต่หากนำเลขเหล่านี้มาจัดเรียงเป็นวงกลมจะได้ดังภาพที่ 2

ภาพที่ 2 การจัดเรียง {A,B,C} เป็นวงกลม

        จากภาพที่ 2 จะเห็นว่าหากเรายึด A เป็นหลักเราสามารถแบ่งวงกลมได้เป็นสองกลุ่มคือ

       กลุ่มที่ 1 ขวามือของ A คือ B และซ้ายมือของ A คือ C ได้แก่วงกลมหมายเลข 1,4 และ 5

       กลุ่มที่ 2 ขวามือของ A คือ C และซ้ายมือของ A คือ B ได้แก่วงกลมหมายเลข 2,3 และ 6

        เราอาจจะเลือก B หรือ C เป็นหลักก็ได้ผลสุดท้ายจะยังคงมีรูปแบบที่แตกต่างกันเพียง 2 แบบ เทคนิคการนับการจัดเรียงเป็นวงกลมจึงต้องทำการยึดสมาชิกไว้ 1 ตัวจากนั้นนำสมาชิกเหลือมาจัดเรียงแบบเชิงเส้น ดังนั้นหากเรามีสิ่งของจำนวน n สิ่ง นำมาจัดเรียงเป็นวงกลมจะได้จำนวนวิธีจัดเรียงทั้งหมด (n – 1)! วิธี

• พิสูจน์สูตรการจัดเรียงแบบวงกลม

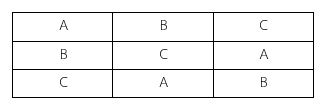
        ดังที่กล่าวมาข้างต้น เรามีเซต {A,B,C} เมื่อทำการจัดเรียงเชิงเส้นจะได้ 3! = 6 วิธี หากเราตัด A ทิ้งจากผลลัพธ์ทั้ง 6 วิธีนี้จะได้ 3{BC,CB} เนื่องจาก {ABC,BCA,CAB} เป็นแบบเดียวกันตามตารางที่ 4 ในทำนองเดียวกันกับ {ACB,CBA,BAC}

ตารางที่ 4 รูปแบบที่สมนัยกันของ {ABC,BCA,CAB}

          โดยที่ {BC,CB} คือเซตของรูปแบบการจัดเรียงแบบวงกลมของ {A,B,C} ได้ 2 แบบคือ {ABC,ACB} เราจะพิจารณากรณีวางนัยยะทั่วไป สมมติให้มีสิ่งของ n สิ่ง {n1,n2,…,nn} ดังนั้นในการจัดเรียงเป็นวงกลมจะเกิดรูปแบบ {n1n2n3…nn, n2n3n…nnn1,...,nnn1n2…n(n-1)} จำนวน n แบบที่เป็นแบบเดียวกันจะได้ว่า n! = n x (การจัดเรียงของnชิ้นแบบวงกลม) การจัดเรียงของnชิ้นแบบวงกลม = n!/n = (n-1)!

ตัวอย่างที่ 9 ต้องการจัดดอกไม้รอบวงเวียนโดยที่ดอกกุหลาบขาว 1 ดอก (wr) และดอกกุหลาบดอก 2 ดอก(rr) จะต้องอยู่ติดกันที่เหลือเป็นดอกไม้ชนิดอื่นๆอีก 12 ชนิด (f1,f2,…,f12) จงหาวิธีการจัดดอกไม้ทั้งหมด

วิธีทำ เนื่องจากดอกกุหลาบทั้งสามจะต้องอยู่ติดกัน { {wr, rr²},f1,f2,…,f12 } ขั้นตอนแรกจัดเรียงสิ่งของเป็นวงกลม 13 สิ่งได้ 12! ขั้นตอนต่อมาการจัดดอกกุหลาบจะได้ 3!/2! = 3 ดังนั้นจำนวนวิธีการจัดเรียงดอกไม้รอบวงเวียนเท่ากับ 3 x 12! แบบ

ตัวอย่างที่ 10 ครอบครัวหนึ่งมีพ่อ (f) แม่ (m) และลูกอีก 4 คน (s1,s2,s3,s4) จงหาวิธีการนั่งทานอาหารบนโต๊ะกลมโดยที่พ่อและแม่นั่งตรงข้ามกัน

วิธีทำ  พิจารณา {f,s1,s2,m,s3,s4} เนื่องจาก พ่อ และ แม่ต้องนั่งตรงข้ามกันจึงเหลือเพียงการจัดเรียง {s1,s2,s3,s4} = 4!

• การจัดเรียงสร้อยข้อมือ

         ในกรณีของสร้อยข้อมือสามารถพลิกกลับด้านได้ทำให้ ABC และ ACB นั้นเป็นแบบเดียวกัน จำนวนรูปแบบของการจัดเรียงสร้อยข้อมือมีค่าเท่ากับ (n-1)! / 2

ตัวอย่างที่ 11 พวกมาลัยที่ทำจากดอกไม้ 12 ชนิดสามารถร้อยได้แตกต่างกันกี่แบบ

วิธีทำ การจัดเรียงแบบวงกลมพลิกกลับได้เท่ากับ (12-1)! / 2 = 11! / 2

 แหล่งที่มา

Faticoni G.T. (2013). Combinatorics an introduction. John Wiley & Sons, Canada.

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

Harnett D.L. (1998). Data, Statistic, and Decision model with excel. John Wiley & Sons, USA.

วีระ ยุคุณธร (2016) เอกสารประกอบการสอนวิชาคณิตศาสตร์เต็มหน่วย มหาวิทยาลัยราชภัฏกาญจนบุรี.

 การจัดกลุ่ม

การเลือกหรือการจัดหมู่เป็นการจัดเรียงแบบไม่สนใจลำดับ ถ้ากำหนดเซต A = {1, 2, 3, 4} หากทำการจัดเรียงเลข 2 หลักจากเลขโดดในเซต A โดยไม่ใช้เลขซ้ำจะได้ P(4,2) = 4! / 2! = 12 จำนวนดังตารางที่ 5

ตารางที่ 5 การสร้างเลข 2 หลักจากเซต A

          แต่หากทำการเลือกจำนวน 2 จำนวนจากเซต A จะพบว่าการเลือก 1 และ 2 เป็นสิ่งเดียวกันกับการเลือก 2 และ 1 นั้นคือ {1, 2} = {2, 1} การเลือกนี้มีความหมายเทียบเท่ากับสับเซตของเซต A ที่มีสมาชิกสองตัวได้แก่ {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4} มีทั้งหมด 6 แบบ เมื่อเราคิดย้อนกลับจะพบว่าหากเรามองการจัดหมู่ให้เป็นลำดับโดยการสลับสมาชิกในเซตที่ถูกเลือกจะทำให้ได้การจัดเรียงเชิงเส้น

• ปัญหาการจัดหมู่

          สมมติให้มีสิ่งของ n สิ่ง  N = {n1, n2, n3,…, nn} ทำการเลือก k สิ่งจะแทนด้วย C(n,k) จะได้เซตในรูปของ {c1, c2, …, ck} เป็นสับเซตของ N ที่มีสมาชิก k ตัว หากเราทำการเรียงสับเปลี่ยน k ตัวนี้จะได้ k! จะเกิดเป็นการจัดเรียงสิ่งของ n สิ่ง k ตำแหน่ง P(n,k) เขียนเป็นสมการได้ดังนี้ C(n,k) x k! = P(n,k) จะได้ว่า C(n,k) = P(n,k) / k! = n! / [ (n - k)!k! ]

ตัวอย่างที่ 12 ในการทดสอบการให้บริการผู้ใช้บริการจำนวน 30 คนถ้าสุ่มตรวจจำนวน 10 คนจะมีวิธีการสุ่มตรวจได้ทั้งหมดกี่วิธี

วิธีทำ เลือกคน 10 คนจากทั้งหมด 30 คนเท่ากับ C(30,10) = 30! / (10! x 20!)

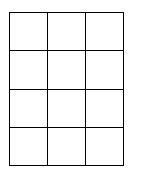
ตัวอย่างที่ 13 กำหนดพื้นที่ขนาด 3x4 ตารางเมตรดังรูป จงหาจำนวนรูปสี่เหลี่ยมมุมฉาก

ขั้นตอนที่ 1 เลือกเส้นแนวตั้งได้ 2 เส้นจาก 4 เส้น C(4,2)

ขั้นตอนที่ 2 เลือกเส้นแนวตั้งได้ 2 เส้นจาก 5 เส้น C(5,2)

จำนวนรูปสี่เหลี่ยมมุมฉากทั้งหมดเท่ากับ C(4,2) x C(5,2) = 60 รูป

คุณสมบัติที่ควรรู้ของ C(n,k) พิจารณา C(100,9) = 100! / [91! 9!] = 100! / [9! 91!] = C(100,91) สังเกตได้ว่า C(n,r) = C(n,k) ถ้า r + k = n เนื่องจาก r = n – k จะได้ C(n,r) = n! / [ (n - r)!r! ] = n! / [ k!(n - k)! ] = C(n,k) หากตีความหมายของ C(n,k) = C(n, n - k) จะแปลความได้ว่าการจัดหมู่หรือเลือกสิ่งของจำนวน k สิ่ง จะทำให้ได้สิ่งของที่ไม่ถูกเลือกจะเกิดเป็นการจัดกลุ่มของสิ่งของที่มีจำนวน n - k สิ่งพร้อมกัน

• จำนวนสเตอร์ลิงชนิดที่สอง

ในกรณีที่เรามีเซต {n1, n2, n3} หากเราต้องการสร้างเซตย่อยที่เป็นผลแบ่งกันจำนวน 2 เซตจะได้ {n1, n2} {n3} / {n1, n3} {n2} / {n2, n3} {n1} จะพบว่ามีจำนวน 3 รูปแบบที่แตกต่างกัน เขียนแทนด้วย S(3,2) เรานิยามจำนวนสเตอร์ลิงชนิดที่ได้สองไว้ดังนี้

S(n,r) = จำนวนรูปแบบของเซตที่มีขนาด n ที่มีผลแบ่งกัน r ส่วน ดังนั้น S(3,2) = 3 แสดงให้เห็นว่าเซตที่มีจำนวนสมาชิก 3 ตัวสามารถแบ่งเป็นผลแบ่งกัน 2 เซตได้ 3 แบบ ในส่วนถัดไปเราจะลองพิจารณาจำนวนสเตอร์ลิงชนิดที่สองเซตที่มีสมาชิกมากกว่า 3 จำนวน พิจารณาเซตที่มีสมชิกจำนวน 4 ตัวคือ {1, 2, 3, 4} พิจารณาค่า S(4,1), S(4,2), S(4,3) และ S(4,4)

          S(4,1) หมายถึงจำนวนรูปแบบของเซตที่มีขนาด 4 ที่มีผลแบ่งกัน 1 ส่วน จะพบว่ามีเพียงเซตเดียวคือ {1, 2, 3, 4} ดังนั้น S(4,1) = 1

          S(4,2) หมายถึงจำนวนรูปแบบของเซตที่มีขนาด 4 ที่มีผลแบ่งกัน 2 ส่วน จะพบว่ามีสองกรณีคือผลแบ่งกันที่มีสมาชิก 1 ; 3 และ 2 ; 2

กรณี 1 ; 3 มีรูปแบบ C(4,1) x C(3,3) = 4 x 1 = 4 ได้แก่

{1} {2, 3, 4} / {2} {1, 3, 4} / {3} {1, 2, 4} / {4} {1, 2, 3}

กรณี 2 ; 2 มีรูปแบบ 3 ได้แก่

{1, 2} {3, 4} / {1, 3} {2, 4} / {1, 4} {2, 3}

ดังนั้น S(4,2) = 7

S(4,3) หมายถึงจำนวนรูปแบบของเซตที่มีขนาด 4 ที่มีผลแบ่งกัน 3 ส่วนตามสัดส่วน 1; 1; 2 จะได้ 

          {1} {2} {3, 4} / {1} {3} {2, 4} / {1} {4} {2, 3}

          {2} {3} {1, 4} / {2} {4} {1, 3} / {3} {4} {1, 2}

สังเกตว่า รูปแบบจะขึ้นอยู่กับจำนวนเซตที่มีสมาชิกสองตัว เนื่องจากสมาชิกที่เหลือจะมีวิธีการเลือกเพียงแบบเดียวนั้นคือ S(4,3) = C(4,2) = 6 S(4,4) หมายถึงจำนวนรูปแบบของเซตที่มีขนาด 4 ที่มีผลแบ่งกัน 4 ส่วน จะพบว่ามีเพียงแบบเดียวคือ {1}, {2}, {3}, {4} ดังนั้น S(4,4) = 1 เมื่อพิจารณาการวางนัยยะทั่วไปของเซต N = {1, 2, 3, …, n} จะพบว่า จำนวนผลแบ่งกั้น  N ที่มี r ส่วน = จำนวนผลแบ่งกั้นที่มี {n} + จำนวนผลแบ่งกั้นที่ไม่มี {n} โดยที่ผลแบ่งกั้นที่มี {n} ซึ่งเหลืออีก r - 1 ส่วนจาก {1, 2, 3, …, n - 1} = S(n - 1,r - 1) และจำนวนผลแบ่งกั้นที่ไม่มี {n} หาได้จากการพิจารณาการนำ { 1, 2, 3, …, n - 1} ไปทำผลแบ่งกั้นจำนวน r ส่วนจะเท่ากับ S(n - 1,r) จากนั้นนำ n ไปแทรกในผลแบ่งกั้นแทรกได้ r ทำให้ได้ว่า  จำนวนผลแบ่งกั้นที่ไม่มี {n} = rS(n - 1,r) เราจึงได้สมการ S(n,r) = S(n - 1,r - 1) + rS(n - 1,r) จากตัวแบบอย่างข้างต้นของเซต {1, 2, 3, 4} จะเห็นว่า S(4,2) = S(3,1) + 2S(3,2) = 1 + 2(3) = 1 + 6 = 7

 แหล่งที่มา

Faticoni G.T. (2013). Combinatorics an introduction. John Wiley & Sons, Canada.

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

Harnett D.L. (1998). Data, Statistic, and Decision model with excel. John Wiley & Sons, USA.

วีระ ยุคุณธร (2016) เอกสารประกอบการสอนวิชาคณิตศาสตร์เต็มหน่วย มหาวิทยาลัยราชภัฏกาญจนบุรี.

 การกระจาย

1. การกระจาย (1 + x)ⁿ และคุณสมบัติ C(n,k)

          ในหัวข้อนี้จะเป็นการศึกษาคุณสมบัติของตัวเลข C(n,k) ที่ได้จากการกระจายทวินามรวมถึงบทพิสูจน์การประยุกต์ รวมถึงเอกลักษณ์ต่างๆในคณิตศาสตร์ด้านการจัดหมู่

พิจารณา (1 + x)ⁿ = C(n,0) + C(n,1)x + C(n,2)x² + … + C(n,n)xⁿ

ถ้าให้ x = 1 จะได้ว่า

2ⁿ = C(n,0) + C(n,1) + C(n,2) + … + C(n,n)

ถ้า n เป็นเลขคี่จะได้ว่า

2ⁿ = 2 [ C(n,0) + C(n,1) + C(n,2) + … + C(n,(n - 1) / 2) ]

ถ้า n เป็นเลขคู่จะได้ว่า

2ⁿ = 2 [C(n,0) + C(n,1) + C(n,2) + … + C(n,n / 2 - 1)] + C(n,n / 2)

จะเห็นว่า (1 + x)ⁿ = sum { C(n,k)x^k }

          เอกลักษณ์ที่ถูกแสดงข้างต้นยังสามารถนำไปอธิบายการพิจารณาจำนวนเซตย่อยของเซตที่มีสมาชิก n ตัวซึ่งมีจำนวนเซตย่อยทั้งหมด 2ⁿ เซตที่แตกต่างกัน เราสามารถจำเป็นออกเป็น n + 1 ประเภทได้แก่ เซตย่อยที่มีสมาชิก 0, 1, 2, …, n ตัวตามลำดับ โดยที่ C(n,k) จะหมายถึงจำนวนเซตย่อยที่มีสมาชิก k ตัว เช่น กำหนดให้ A = {0, 1, 2, 3, …, 9} แล้วจำนวนเซตย่อยของ A ที่มีสมาชิก 0, 1, 2, …, 10 ตัวจะเท่ากับ

C(10,0) จำนวนเซตย่อยที่ได้จากการเลือกสมาชิก 0 จากสมาชิกในเซต A 10 ตัว

C(10,1) จำนวนเซตย่อยที่ได้จากการเลือกสมาชิก 1 จากสมาชิกในเซต A 10 ตัว

C(10,2) จำนวนเซตย่อยที่ได้จากการเลือกสมาชิก 2 จากสมาชิกในเซต A 10 ตัว

 …

C(10,10) จำนวนเซตย่อยที่ได้จากการเลือกสมาชิก 10 จากสมาชิกในเซต A 10 ตัว เมื่อพิจารณาจำนวนเซตย่อยทั้งหมดจะเท่ากับ C(10,0) + C(10,1) + C(10,2) + … + C(10,10) = 2¹⁰ ตามเอกลักษณ์ที่กล่าวมา 

ต่อมากเราลองพิจารณาอนุพันธ์ (1 + x)ⁿ เทียบ x จะได้

d(1 + x)ⁿ / dx = d[sum_k=0,n {C(n,k)x^k}] / dx

  n(1 + x)^{n - 1} = sum_k=0,n {k*C(n,k)x^{k – 1}}

ถ้าให้ x = 1 จะได้

n2^{n - 1} = sum_k=0,n {k*C(n,k)}

 2^{n - 1} = sum_k=0,n {k*C(n,k)} / n

= [C(n,1) + 2C(n,2) + 3C(n,3) + … + n] / n

          จะเห็นว่าเราได้เอกลักษณ์ของคณิตศาสตร์ด้านการจัดหมู่เพิ่มเติมในทางแคลคูลัสมีการใช้ทฤษฎีทวินามพิสูจน์สูตรการหาอนุพันธ์ของฟังก์ชันยกกำลังสมมติให้ f(x) = xⁿ สมมติให้ x มีการเปลี่ยนแปลงเพิ่มขึ้นแบบน้อยมากมากชนิดเข้าใกล้ศูนย์โดยแทนปริมาณการเพิ่มดังกล่าวด้วย dx เราจะพิจารณาว่าค่าของฟังก์ชันจะเปลี่ยนแปลงไปเท่าใด เริ่มจากการพิจารณา

f(x + dx)

= (x + dx)ⁿ

= xⁿ + C(n,1)x^{n - 1}dx + C(n,2)x^{n - 2}(dx)² + … + C(n,n)(dx)ⁿ

= f(x) + (C(n,1)xⁿ  + C(n,2)x^{n - 1}(dx) + … + C(n,n)(dx)^{n - 1})dx

จะเห็นได้ว่า f(x + dx) ประมาณได้ด้วย

f(x) + (C(n,1)x^{n - 1})dx = f(x) + nx^{n - 1}(dx)

ในแคลคูลัสปริมาณ (dx)ⁿ เมื่อ n > 1 ประมาณได้ด้วย 0 เนื่องจากมีค่าน้อยมาก จะเห็นว่า  [f(x+dx) – f(x)] / dx ถูกนิยามเป็นอนุพันธ์ของฟังก์ชัน สรุปได้ว่า df/dx = nx^{n – 1}

*หมายเหตุแคลคุลัสที่ผู้เขียนใช้อธิบายเป็นแคลคูลัสที่ไม่มีลิมิตเป็นที่รู้จักกันในชื่อ infinitesimal calculus หรือ nonstandard calculus การคำนวณจะอยู่บนระบบจำนวนจริงไฮเปอร์ (hyper real number system) ซึ่งนิยามใช้ในการวิเคราะห์งานทางด้านกลศาสตร์ความต่อเนื่อง

          นอกจากนี้เอกลักษณ์ดังกล่าวสามารถนำไปช่วยพิจารณาการหาเศษจากการหาร ถ้าเราพิจารณาเศษที่เกิดจากการนำ 2563²⁰²⁰ หารด้วย 4 เราเขียน 2563 ได้ในรูปของ 2563 = 4(640) + 3 ดังนั้นการพิจารณาเศษจากการหาร 2563²⁰²⁰ = [4(640) + 3]²⁰²⁰ เมื่อกระจายทวินามแล้วจะพบว่า มีเพียงพจน์ C(2020,0)3²⁰²⁰ ที่ไม่มี 4 เป็นตัวประกอบจึงเพียงพอที่จะพิจารณาเศษจาก 3²⁰²⁰ ยิ่งไปกว่านั้น หากเราเขียน 2563²⁰²⁰ = [4(641) + (- 1)]²⁰²⁰ จะเห็นได้โดยง่ายว่าการพิจารณาเศษสามารถพิจารณาได้จาก (-1)²⁰²⁰ จะได้เศษเท่ากับ 1

         จะเห็นว่าทฤษฎีบททวินามนั้นมีบทประยุกต์ใช้ทั้งในด้านคณิตศาสตร์เองอาทิ แคลคูลัส และทฤษฎีจำนวนซึ่งเป็นเครื่องมือวิทยาศาสตร์ วิศวกรรม ตลอดจนการวิเคราะห์ข้อมูล ผลตอบแทนด้านธุรกิจและเศรษฐศาสตร์ เป็นต้น

สำหรับคุณสมบัติของจำนวน C(n,k) ยังมีคุณสมบัติที่น่าสนใจตามที่กล่าวไว้ในหัวข้อที่ 5 ผู้เขียนจะแสดงวิธีการพิสูจน์คุณสมบัติดังนี้

คุณสมบัติ 1 C(n,k) + C(n,k + 1) = C(n + 1,k + 1)

พิสูจน์

พิจารณา C(n,k) + C(n,k + 1) โดยนิยามจะได้ว่า

C(n,k) + C(n,k + 1) = n!/[(k!)(n – k)!] + n! / [(k + 1)!(n – k – 1)!]

ดึงตัวร่วม n! / [(k!)(n – k – 1)!] จะได้

C(n,k) + C(n,k + 1)

= n! / [(k!)(n – k – 1)!] * [1 / (n – k) + 1 / (k + 1)]

จัดรูป RHS ให้อยู่ในรูปอย่างง่าย

[1 / (n – k) + 1 / (k + 1)] = [(k + 1 + n – k) / ((n – k)*(k + 1))]

                                      = [(n + 1) / ((n – k)*(k + 1))]

จะได้ว่า

C(n,k) + C(n,k + 1)

= n! / [(k!)(n – k – 1)!] *[(n + 1) / ((n – k)*(k + 1))]

= [n! (n + 1)] / [(k!)*(n – k – 1)!*(n – k)*(k + 1))]

= (n + 1)! / [(n – k)!*(k + 1)!]

= (n + 1)! / [((n + 1) – (k + 1))!*(k + 1)!]

= C(n + 1,k + 1)

ตัวอย่างที่ 16 ค่าของ C(10,6) + C(10,7) = C(11,7)

สามารถแสดงวิธีการคำนวณโดยละเอียดได้ดังนี้

C(10,6) + C(10,7)

= 10! / [6!*4!] + 10! / [7!*3!]

          = [10! / (6!*3!) ]*[1/4 + 1/7]

          = [10! / (6!*3!) ]*[11/(7*4)]

            = (11*10!) / (7*6!*4*3!)

          = 11!/[7!*4!]

          = C(11,7) = C(11,4)

ตัวอย่างที่ 17 จงหาค่าของ C(10,3) + 2C(10,4) + C(10,5)

วิธีทำ การทำวิธีคำนวณโดยตรงแบบตัวอย่างที่ 16 ค่อยข้างมีความซับซ้อนในการคำนวณ การใช้คุณสมบติข้อที่ 1 สามารถช่วยลดความซับซ้อนในการตรวจสอบค่าจากการคำนวณได้เราพิจารณา

C(10,3) + 2C(10,4) + C(10,5)

= [ C(10,3) + C(10,4) ] + [ C(10,4) + C(10,5) ]

= C(11,4) + C(11,5) 

= C(12,5)

พิจารณา

C(11,7) = C(10,7) + C(10,6)

= C(9,7) + C(9,6) + C(10,6)

= C(8,7) + C(8,6) + C(9,6) + C(10,6)

= C(7,7) + C(7,6) + C(8,6) + C(9,6) + C(10,6)

= C(6,6) + C(7,6) + C(8,6) + C(9,6) + C(10,6)

จะได้คุณสมบัติข้อที่ 2 ซึ่งคุณสมบัติข้อนี้ผู้เขียนละการพิสูจน์ผู้อ่านสามารถศึกษาเพิ่มเติมได้จาก (Faticoni, 2013).

คุณสมบัติ 2

C(k,k) + C(k + 1,k) + C(k + 2,k) + … + C(n,k) = C(n + 1,k + 1)

ตัวอย่างที่ 18 พิจารณา

C(1,1) + C(2,1) + C(3,1) + … + C(n,1) = C(n + 1,2) = (n + 1)! / [ 2! x (n - 1)! ] = n(n + 1)/2

จะเห็นว่าเป็นไปตามผลบวกของเกาส์

1 + 2 + 3 + … + n = n(n + 1)/2

แหล่งที่มา

Faticoni G.T. (2013). Combinatorics an introduction. John Wiley & Sons, Canada.

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

Harnett D.L. (1998). Data, Statistic, and Decision model with excel. John Wiley & Sons, USA.

วีระ ยุคุณธร (2016) เอกสารประกอบการสอนวิชาคณิตศาสตร์เต็มหน่วย มหาวิทยาลัยราชภัฏกาญจนบุรี.

ทฤษฏีบททวินาม

          จากที่กล่าวมาข้างต้น เราสามารถนำเรื่องการจัดกลุ่มมาศึกษาการกระจายนิพจน์ (x + y)ⁿ โดยที่ n เป็นจำนวนเต็มบวกหรือศูนย์ เรียกว่าการกระจายนี้ว่าการกระจายทวินาม โดยค่าสัมประสิทธิ์จะแสดงถึงจำนวนรูปแบบทั้งหมดของการจัดกลุ่มที่เกิดจากการเลือกนิพจน์พจน์หน้าและนิพจน์พจน์หลัง

พิจารณานิพจน์ต่อไปนี้

      (x + y)⁰ = 1

      (x + y)¹ = x + y

      (x + y)² = (x + y)(x + y) = xx + xy + yx + yy = x² + 2xy + y²

      (x + y)³ = (x + y)(x + y)(x + y) = xxx + xyx + yxx + yyx + xxy + xyy + yxy + yyy

                  = x³ + 3x²y + 3xy² + y³

           สังเกตได้ว่าค่าสัมประสิทธิ์ของ x²y เท่ากับการเรียงสับเปลี่ยน {x,x,y} = 3!/2! หากเราพิจารณาในกรณีที่เป็น x^ky^{n - k} จะได้ค่าสัมประสิทธิ์คือ n! / [ k!(n - k)! ] = C(n,k) ดังนั้นการกระจายทวินาม

            (x + y)ⁿ = C(n,n)xⁿy⁰ + C(n,n-1)x^n-1y¹ + C(n,n-2)x^n-2y² + … + C(n,2)x²y^n-2 + C(n,1)x¹y^n-1 + C(n,0)x⁰yⁿ

           ตีความ C(n,k) สำหรับ (x + y)ⁿ ได้ว่าเป็น เลือก x จำนวน k ตัวและเลือก y จำนวน n – k ตัว

ตัวอย่างที่ 14 จงหาสัมประสิทธิ์ของพจน์ x⁸y¹⁸ จากการกระจาย (4x² – 3y³)¹⁰

วิธีทำ เนื่องจากต้องการพจน์ x⁸ จะต้องทำการเลือก 4x² จำนวน 4 พจน์จาก 10 พจน์และเลือก 3y³ จำนวน 6 พจน์จะได้สัมประสิทธิ์ของพจน์ x⁸y¹⁸ คือ C(10,4) x 4⁴ x (-3)⁶ = C(10,4) x 4⁴ x 3⁶

ตัวอย่างที่ 15 จงหาพจน์ค่าคงที่จากการกระจาย (4x² – 3 / x³)²⁰

วิธีทำ พจน์ค่าคงที่จะเกิดขึ้นเมื่อมีการเลือกพจน์หน้าและพจน์หลังในสัดส่วน 3:2 โดยรวมกันเท่า 20 พจน์ จะได้ว่า 3k+2k = 20 พบว่า k = 4 นั้นคือจะต้องเลือกพจน์แรก 12 พจน์และเลือกพจน์หลัง 8 พจน์จะได้สัมประสิทธิ์คือ C(20,12) x 4¹² x 3⁸

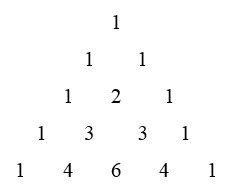
         หากเราพิจารณาค่าตัวเลขจากการแยกสัมประสิทธิ์ออกจากตัวแปรจะได้ของการกระจายทวินามนิพจน์ (x + 1)ⁿ เมื่อ n = 0, 1, 2, 3 และ 4 ตามลำดับ เราสังเกตได้ง่ายว่า

          เราเรียกสามเหลี่ยมข้างต้นว่าสามเหลี่ยมปาสคาลซึ่งปรากฏในประวัติศาตร์คณิตศาสตร์ทั้งในกรีก จีน และอินเดีย ก่อนที่แบลส ปาสคาลจะเผยแพร่สามเหลี่ยมดังกล่าว โดยค่าตัวเลขของสามเหลี่ยมแสดงถึงค่าสัมประสิทธิ์ของการกระจายนิพจน์ โดยสามเหลี่ยมปาสคาลนี้ยังเกี่ยวกับกับเนื้อหาทางคณิตศาสตร์อีกมากมายอาทิ จำนวนเฉพาะ ลำดับฟิโบนักซี จำนวนเชิงรูปหลายเหลี่ยม และจำนวนจุดบนวงกลมเป็นต้น แต่ในที่นี้อยู่เขียนจะศึกษาเพียงสามเหลี่ยมปาสคาลที่เกี่ยวกับกับการกระจายทวินาม พิจารณาสัมประสิทธิ์การกระจายทวินามกรณีเลขชี้กำลังเท่ากับ n = 0, 1, 2 และ 3 จากสามเหลี่ยมปาสคาล

            กรณี n = 0    จะได้พจน์เดียวคือ 1

            กรณี n = 1    จะได้สัมประสิทธิ์เป็น 1 และ 1

            กรณี n = 2    จะได้พจน์แรก และ พจน์สุดท้าย คือ 1 จะได้พจน์ที่ 2 จาก พจน์ที่ 1 และ พจน์ที่ 2 ของกรณี n = 1 

            กรณี n = 3    จะได้พจน์แรก และ พจน์สุดท้าย คือ 1 จะได้พจน์ที่ 2 จาก พจน์ที่ 1 และ พจน์ที่ 2 ของกรณี n = 2

                                จะได้พจน์ที่ 3 จาก พจน์ที่ 2 และ พจน์ที่ 3 ของกรณี n = 2

      สังเกตกรณีที่ n ทั่วไปจะได้พจน์ที่ k จาก พจน์ที่ k - 1 และ พจน์ที่ k ของกรณี n - 1 นั้นคือ  C(n,k) = C(n - 1,k - 1) + C(n - 1,k) หรือ 

C(n + 1,k + 1) = C(n,k) + C(n,k + 1)

       ซึ่งจะแสดงวิธีการพิสูจน์ไว้ในหัวข้อถัดไป

           การแจงแจกทวินาม

          การแจกแจงทวินามถูกนำไปประยุกต์ใช้ในเรื่องของความน่าจะเป็นซึ่งมีเงื่อนไข 5 ข้อดังนี้ 1) ผลลัพธ์ที่ได้จากการทดลองจะต้องออกมาเป็นสำเร็จ (S) หรือไม่สำเร็จ (F) อย่างใดอย่างหนึ่ง 2) มีจำนวนครั้งในการทดลองจำกัดในที่นี้เราสมมติให้มีการทดลองจำนวน n ครั้ง 3) ผลลัพธ์จากการทดลองในแต่ละครั้งอิสระต่อกัน 4) สมมติให้ความน่าจะเป็นที่จะสำเร็จ P(S) = s และให้ความน่าจะเป็นที่จะไม่สำเร็จ P(F) = f = 1 - s และ 5) ให้ X คือผลรวมความสำเร็จของตัวแปรสุ่มที่เราสนใจ ถ้าสมมติให้เราทำการทดลอง n ครั้งและสนใจโอกาสสำเร็จ k ครั้ง นั้นคือความน่าจะเป็นที่จะสำเร็จจะได้รูปแบบการกระจายดังนี้ {s, s, …, s} := k ครั้ง และ {f, f, …, f} := n - k ครั้ง จากทฤษฎีความน่าจะเป็นเราพบว่า 1 = s + f = (s + f)ⁿ

         ดังนั้นจำนวนวิธีที่ทำการทดลอง n ครั้งแล้วได้ผลลัพธ์สำเร็จ k ครั้งจะเท่ากับ C(n,k) จะได้ฟังก์ชันมวลความน่าจะเป็น p.m.f: P(X = k) = C(n,k)s^kf ^{n - k} = C(n,k)s^k(1 – s)^{n – k}

          ตัวอย่างเช่นในการลงทุนของบริษัทแห่งหนึ่งเมื่อประมาณความเสี่ยงในการลงทุนแต่ละครั้งพบว่าในการลงทุนแต่ละครั้งจะมีโอกาสที่จะได้กำไรประมาณ 10,000 บาทประมาณ 70 % นั้นคือมีโอกาสได้กำไร 0 บาทคิดเป็น 30 %  หากเราทำการลงทุนจำนวน 3 ครั้งและสนใจความเสี่ยงและผลกำไรที่ได้จากการลงทุนสามารถ คำนวณได้ดังนี้

          ในการลงทุนจำนวน 3 ครั้ง (n = 3) แต่ละครั้งมีผลลัพธ์ {S,F} โดยที่ P(S) = s = 0.7 และ P(F) = f = 0.3 จะมีรูปแบบการเกิดเหตุการณ์ได้ดังนี้

           โอกาสสำเร็จ 0 ครั้ง { FFF } หรือความน่าจะเป็น P(X = 0) C(3,0)f⁰ = 0.33 = 0.027 และได้กำไร 0 บาท สำเร็จ 1 ครั้ง { SFF, FSF, FFS } หรือความน่าจะเป็น P(X = 1) C(3,1)sf² = C(3,1)(0.7)(0.3)² = 3(0.7)(0.3)² = 0.189 และได้กำไร  10,000 บาท

           สำเร็จ 2 ครั้ง { SSF, SFS, FSS } หรือความน่าจะเป็น P(X = 2) C(3,2)s²f = C(3,2)(0.7)²(0.3) = 3(0.7)²(0.3) = 0.441 และได้กำไร 20,000 บาท

           สำเร็จ 3 ครั้ง { SSS } หรือความน่าจะเป็น P(X = 3) C(3,3)s³ = 0.73 = 0.343 และได้กำไร 30,000 บาท

           ดังนั้นผลตอบแทนเฉลี่ยหรือกำไรที่คาดว่าจะได้รับ(ค่าคาดหวัง)ของการลงทุนครั้งนี้จะพบว่า 

          มีโอกาส 0.027 = 2.7 % ที่จะได้กำไร 0 บาท

          มีโอกาส 0.189 = 18.9 % ที่จะได้กำไร 10,000 บาท

          มีโอกาส 0.441 = 44.1 % ที่จะได้กำไร 20,000 บาท

          มีโอกาส 0.343 = 34.3 % ที่จะได้กำไร 30,000 บาท

          เฉลี่ยแล้วคิดเป็น 0.027(0) + 0.189(10k) + (0.441)(20k) + (0.343)(30k) = 21,000 บาท

          นอกจากนี้เรายังสามารถวิเคราะห์ส่วนเบี่ยงเบนมาตรฐานและค่าความแปรปรวนได้อีกด้วยแต่ผู้เขียนจะไม่กล่าวถึงในที่นี้ ผู้อ่านสามารถศึกษาเพิ่มเติมในบทเรียนสถิติเรื่องการกระจายตัวแบบทวินาม

แหล่งที่มา

Faticoni G.T. (2013). Combinatorics an introduction. John Wiley & Sons, Canada.

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

Harnett D.L. (1998). Data, Statistic, and Decision model with excel. John Wiley & Sons, USA.

วีระ ยุคุณธร (2016) เอกสารประกอบการสอนวิชาคณิตศาสตร์เต็มหน่วย มหาวิทยาลัยราชภัฏกาญจนบุรี.