เซต (Set)
2 - แผนภาพของเวนน์–ออยเลอร์ และการดำเนินการของเซต
แผนภาพของเวนน์–ออยเลอร์ (Venn-Euler Diagram)
เป็นแผนภาพที่นิยมใช้เขียนเพื่อแสดงความสัมพันธ์ของเซต เพื่อให้ดูง่ายและชัดเจนมากขึ้น ปกติจะกำหนดเอกภพสัมพัทธ์![]() ด้วยกรอบสี่เหลี่ยมมุมฉาก ภายในนั้นมีเซตซึ่งอาจเขียนเป็นวงกลม วงรี หรือรูปปิดอื่นๆ
ด้วยกรอบสี่เหลี่ยมมุมฉาก ภายในนั้นมีเซตซึ่งอาจเขียนเป็นวงกลม วงรี หรือรูปปิดอื่นๆ
สมมติเรามีเซตต่างๆ ดังภาพต่อไปนี้
จากรูป (a): A = {1, 2} B = {3, 4, 5} จะเห็นได้ว่า A และ B ไม่มีสมาชิกร่วมกันเลย
ส่วนรูป (b): C = {a, b,c,d} D = {c,d, e, f, g} จะเห็นได้ว่าทั้งสองเซตนี้มีสมาชิกบางตัวร่วมกัน
สำหรับรูป (c): E = {1,2, 3} F = {1,2} หรือกล่าวได้ว่า Fhttp://www.w3.org/1998/Math/MathML¨»«mo»§#8834;«/mo»«/math»"
การดำเนินการของเซต (Set Operations)
การดำเนินการของเซตจะทำให้ได้เซตใหม่เกิดขึ้น (แสดงด้วยส่วนที่แรเงาสีเทา) หลักๆแล้วมีอยู่ 4 แบบ ดังนี้
1)ยูเนี่ยน(Union): ทำให้เกิดเซตใหม่ซึ่งสมาชิกมาจากทั้งสองเซต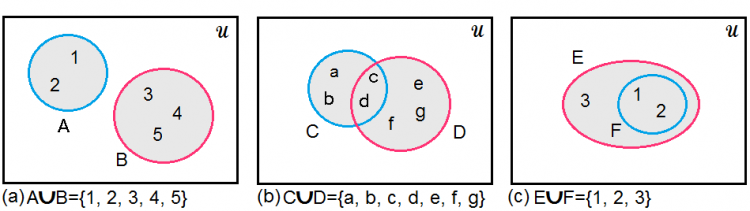
2)อินเตอร์เซกชั่น(Intersection): เซตใหม่ที่ได้เป็นสมาชิกร่วมกันของทั้งสองเซต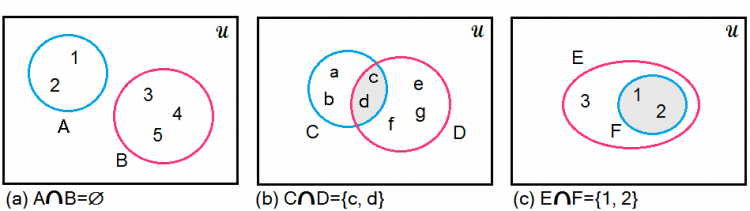
3)ผลต่าง(Difference): ถ้าหาผลต่างของ A-B จะได้เซตผลลัพธ์เป็นเซตที่ประกอบด้วยสมาชิกที่อยู่ใน A แต่ไม่อยู่ใน B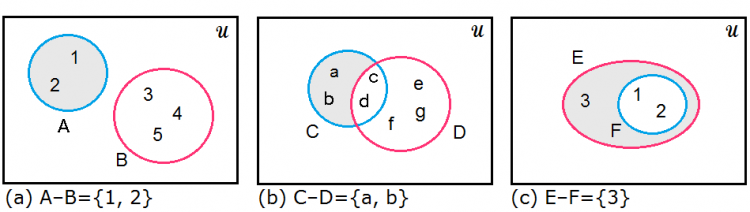
4)คอมพลีเมนต์(Complement): คอมพลีเมนต์ของ A เขียนแทนด้วย A’ คือสมาชิกทุกตัวที่เหลือในเอกภพสัมพัทธ์ยกเว้น A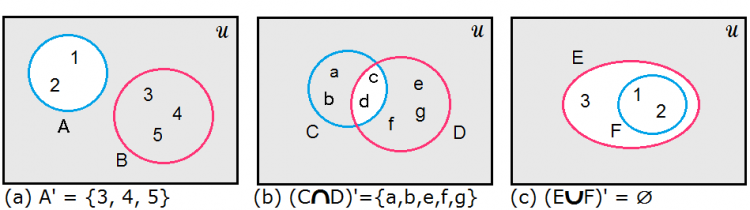
กลับไปที่เนื้อหา
คุณสมบัติบางประการที่สำคัญเกี่ยวกับการดำเนินการของเซต มีดังนี้ค่ะ
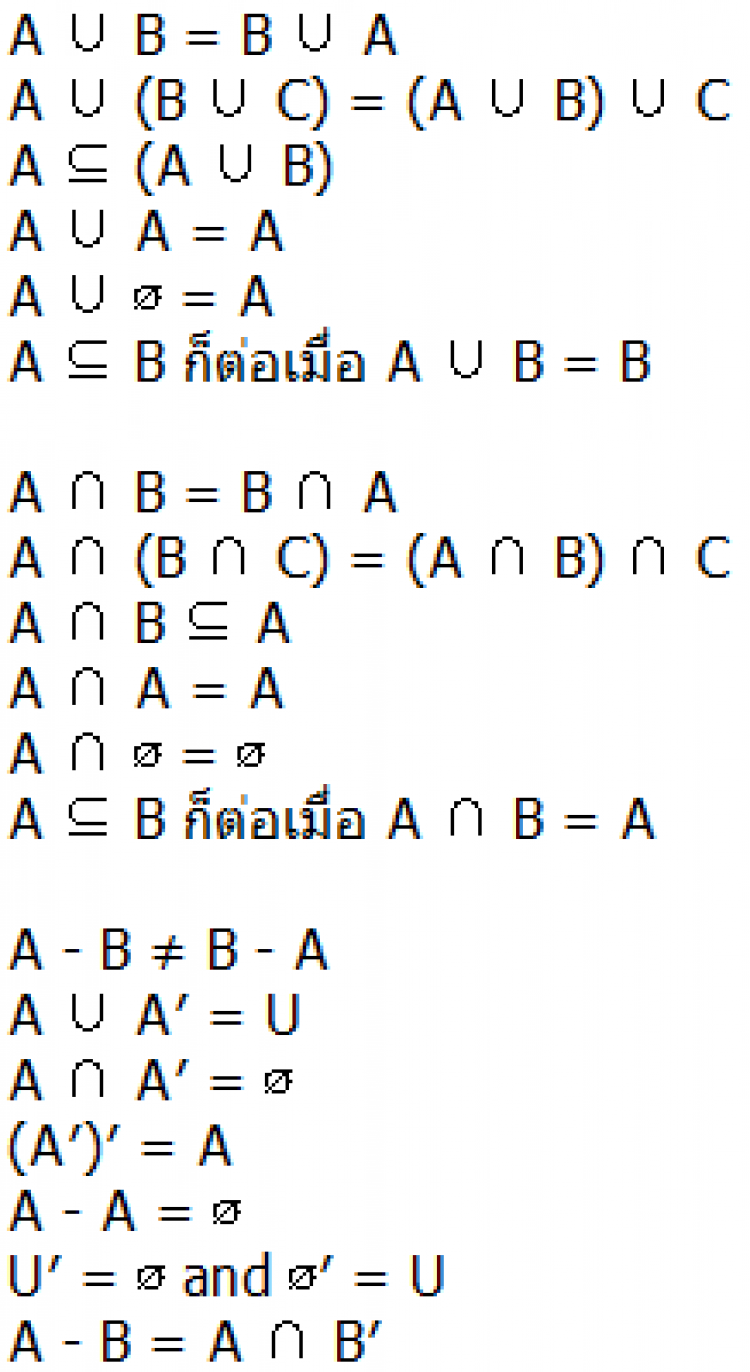
ครูแนะนำว่าควรวาดภาพเซตของเวนน์-ออยเลอร์ควบคู่กันไปกับการทำความเข้าใจคุณสมบัติเหล่านี้นะคะ หลีกเลี่ยงการท่องให้มากที่สุดเพราะนั่นจะทำให้เราจำได้แป๊บเดียว พอสอบก็ลืมหมดค่ะ ^_^
กลับไปที่เนื้อหา
หลังจากที่เราทราบแล้วว่าเซตคืออะไร มีการดำเนินการอย่างไร หลายคนอาจจะยังคิดไม่ออกว่าแล้วจะเอาเซตไปใช้ประโยชน์อะไรได้บ้าง ลองดูตัวอย่างการแก้ปัญหาที่เกี่ยวกับเซตต่อไปนี้กันนะคะ
Ex 1ในการสอบถามความชอบเรื่องสี ในกลุ่มเด็กป.1 จำนวน 44 คน พบว่า ชอบสีชมพู 12 คน ชอบสีฟ้า 9 คน ชอบทั้งสองสี 4 คน อยากทราบว่ามีเด็กกี่คนที่ไม่ชอบสีทั้งสองเลย
Soln ครูจะอธิบายการคิดเป็นขั้นๆ เพื่อให้ง่ายต่อการทำความเข้าใจและเห็นภาพชัดเจนยิ่งขึ้นนะคะ
ขั้นที่หนึ่งข้อนี้กำหนดกลุ่มเด็กป.1 มาให้ ดังนั้นในขั้นนี้เราจึงทราบว่าเอกภพสัมพัทธ์คือเด็กป.1 จำนวน 44 คน
ขั้นที่สองลองดูว่ามีเซตที่แตกต่างกันกี่เซต จะได้ทราบว่าจะวาดแผนภาพเวนน์-ออยเลอร์อย่างไร
เซตที่ 1 คือเซตของเด็กที่ชอบสีชมพู
เซตที่ 2 คือเซตของเด็กที่ชอบสีฟ้า
ส่วนคำว่า “ชอบทั้งสองสี” ไม่ใช่เซตใหม่ แต่หมายถึงทั้งสองเซตข้างบนมีความเกี่ยวข้องกันแบบ intersection
สรุปว่า มีเซต 2 เซตในเอกภพสัมพัทธ์นี้
ขั้นที่สามการแก้ปัญหาเรื่องเซต ครูแนะนำให้ลองวาดแผนภาพเวนน์-ออยเลอร์เสมอ เพราะถ้าวาดได้จะทำให้การแก้ปัญหาง่ายและสนุกขึ้นมากเลยค่ะ ^_^
- วาดกรอบสี่เหลี่ยมขึ้นมาเพื่อกำหนดเอกภพสัมพัทธ์ จากนั้นวาดรูปปิด (แนะนำวงกลมหรือวงรี) เพื่อแทนเซตทั้งสองที่ได้ในขั้นก่อนหน้านี้ เขียนชื่อเซตกำกับไว้ด้วยจะได้ไม่งงว่าวงไหนแทนเซตอะไร และที่สำคัญให้แทนจำนวนสมาชิกของเซตลงไปในวงปิดนั้นด้วย
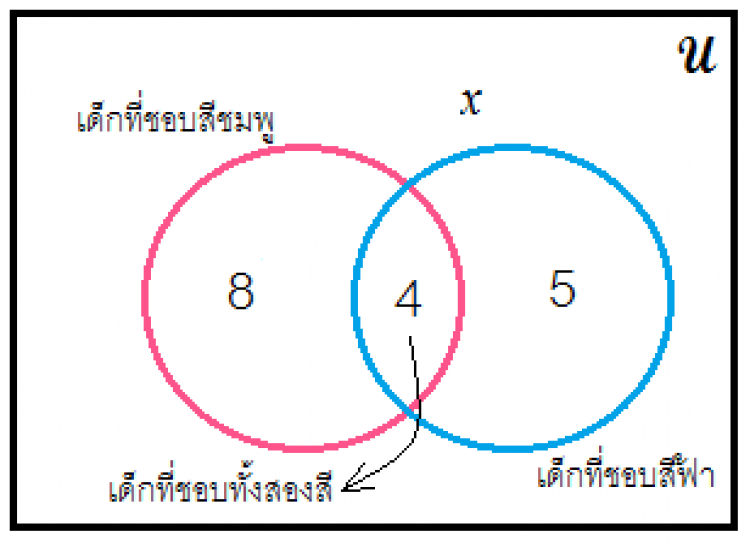
- จะเห็นได้ว่า เซตของเด็กที่ชอบสีชมพูมีจำนวน 12 คน แต่ครูแยกใส่จำนวนเด็กที่ชอบสีชมพูอย่างเดียว 8 คน กับเด็กที่ชอบสีชมพูกับสีฟ้า (ส่วนที่ intersection ของทั้งสองเซต) อีก 4 คนเพราะ 8+4=12 คน
- เซตของเด็กที่ชอบสีฟ้าก็เช่นกัน ครูแยกจำนวนเด็กที่ชอบสีฟ้าอย่างเดียว 5 คน กับที่ชอบทั้งสีฟ้าและสีชมพูอีก 4 คน รวมเป็น 5+4=9 คน
-เช็คเอกภพสัมพัทธ์ อย่าลืมว่าเด็กทั้งหมดมี 44 คน ดังนั้นจำนวนสมาชิกของทุกเซตรวมกันภายใต้เอกภพสัมพัทธ์นี้จะต้องไม่หายไปไหน นั่นคือ 8+4+5+x= 44 (เด็กที่ไม่ชอบทั้งสองสีนี้เลย ก็คือxนั่นเองค่ะ)
-จะได้ว่าx= 44 – 8 – 4 – 5 = 27
เพราะฉะนั้นจำนวนเด็กที่ไม่ชอบทั้งสองสีนี้เลยเท่ากับ 27 คนAns
******************************************************************************
Ex 2ในการสำรวจคะแนนนิยมจากผู้ชมละคร 100 คนที่มีต่อละคร 3 เรื่องคือดอกมะม่วงสีทอง วนาลัย ชื่นชีวันนาวี โดยที่ผู้ชมจะต้องแสดงความนิยมให้อย่างน้อย 1 เรื่อง ปรากฏว่า ดอกมะม่วงสีทองได้รับคะแนนนิยมมากกว่าวนาลัยอยู่ 6 คะแนน และสามารถเขียนแผนภาพได้ดังรูป
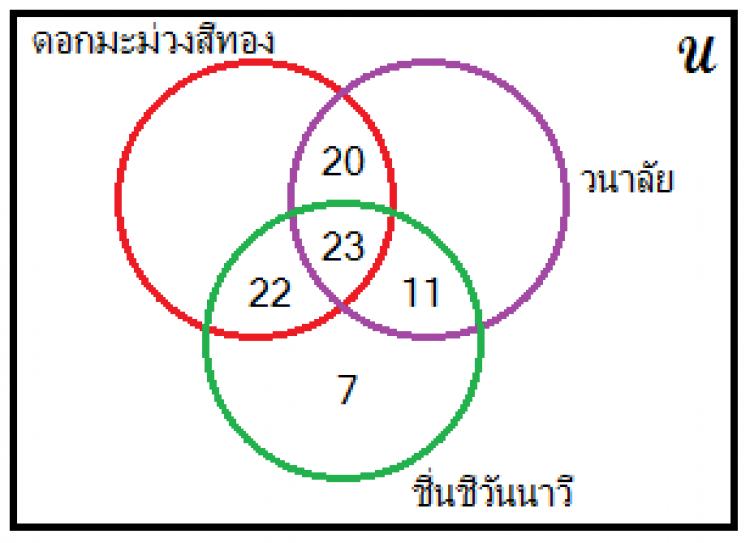
ข้อใดต่อไปนี้ผิด
ก. ผู้ชมชอบละครวนาลัยน้อยที่สุด
ข. ผู้ชมที่ชอบเฉพาะเรื่องดอกมะม่วงสีทอง มี 10 คน
ค. ผลรวมของผู้ชมที่ชอบละครเพียงเรื่องเดียว เท่ากับ 24
Soln
จำนวนในส่วนที่เราไม่ทราบตอนนี้ คือผู้ชมที่ชอบดอกมะม่วงสีทองเพียงเรื่องเดียว (พื้นที่ว่างในวงสีแดง สมมติแทนด้วย x) กับ ผู้ชมที่ชอบวนาลัยเพียงเรื่องเดียว (พื้นที่ว่างในวงสีม่วง สมมติแทนด้วย y)
เราทราบว่าเอกภพสัมพัทธ์คือผู้ชมจำนวน 100 คน ดังนั้น
x+20+23+22+11+y+7 = 100 ……………………….(1)
ดอกมะม่วงสีทองได้รับคะแนนนิยมมากกว่าวนาลัยอยู่ 6 คะแนน นั่นก็คือ
x+20+23+22 – (y+20+23+11) = 6……………………….(2)
จากสมการ (1) จะได้ x+y = 17
จากสมการ (2) จะได้ x-y = -5
เมื่อแก้สมการทั้งสองแล้วจะได้ x=6, y=11
แสดงแผนภาพเซตที่มีจำนวนสมาชิกครบสมบูรณ์ได้ดังนี้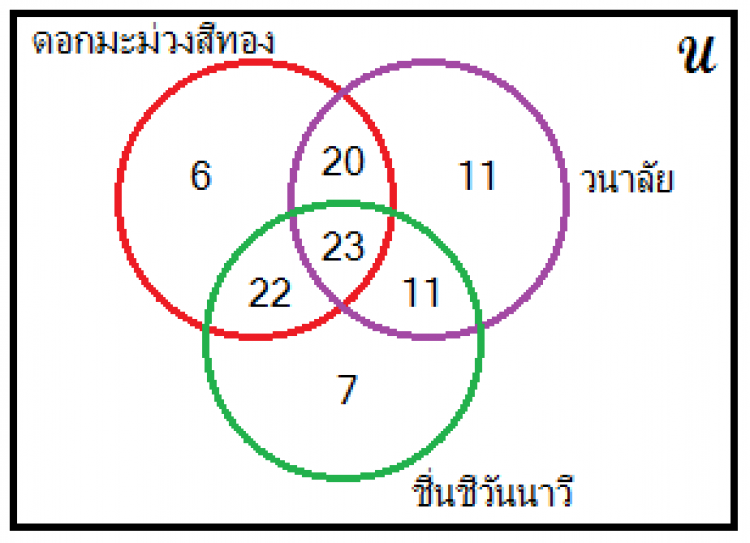
พิจารณาคำกล่าวในแต่ละข้อ
ก. ผู้ชมชอบละครวนาลัยน้อยที่สุด
จำนวนรวมของผู้ที่ชอบละครดอกมะม่วงสีทอง = 6+20+23+22 = 71 คน
จำนวนรวมของผู้ที่ชอบละครวนาลัย = 11+20+23+11 = 65 คน
จำนวนรวมของผู้ที่ชอบละครชื่นชีวันนาวี = 23+22+11+7 = 63 คน
ดังนั้นข้อ ก. จึงผิดAns
ข. ผู้ชมที่ชอบเฉพาะเรื่องดอกมะม่วงสีทอง มี 10 คน
จากที่เราหาได้ จะเห็นได้ว่าผู้ชมที่ชอบเฉพาะเรื่องดอกมะม่วงสีทองมี 6 คน ดังนั้นข้อ ข. จึงผิด Ans
ค. ผลรวมของผู้ชมที่ชอบละครเพียงเรื่องเดียว เท่ากับ 24
จำนวนผู้ชมที่ชอบละครเรื่องเดียว = 6+11+7 = 24 ดังนั้นข้อ ค. ถูกต้อง
กลับไปที่เนื้อหา



