การประยุกต์ใช้กำหนดการเชิงเส้น

กำหนดการเชิงเส้นสามารถนำไปใช้แก้ปัญหาเกี่ยวกับการจัดการทรัพยากรที่มีอยู่อย่างจำกัด ให้ได้ประโยชน์สูงสุดได้อย่างมากมาย นับตั้งแต่ในระดับเล็ก ๆ เช่นการค้าขายระดับครัวเรือน ไปจนถึงกิจการขนาดใหญ่ระดับบริษัทมหาชน ในที่นี้จะแสดงตัวอย่างการประยุกต์ใช้กำหนดการเชิงเส้น 3 ตัวอย่างดังนี้

ตัวอย่างที่ 1แม่ค้าคนหนึ่งทำทุเรียนกวนส่งไปขายที่ห้างสรรพสินค้า และร้านสะดวกซื้อ โดยบรรจุขายชิ้นละ 500 กรัม โดยทุเรียนกวนที่ส่งไปขายยังห้างสรรพสินค้า เป็นทุเรียนกวน 100 % คุณภาพดีไม่ผสมแป้ง มีต้นทุนอยู่ที่ชิ้นละ 60 บาท ส่งขายในราคาชิ้นละ 150 บาท แต่ส่งขายได้ ไม่เกิน 1,000 ชิ้น ในขณะที่ทุเรียนกวนที่ส่งไปขายยังร้านสะดวกซื้อเป็นทุเรียนกวนที่ผสมแป้ง มีต้นทุนอยู่ที่ชิ้นละ 30 บาท ส่งขายชิ้นละ 70 บาท และส่งขายได้ไม่เกิน 3,000 ชิ้น แม่ค้ามีต้นทุนอยู่เพียง 120,000 บาท แม่ค้าควรจะทำทุเรียนกวนชนิดไหนส่งให้ห้าง สรรพสินค้าและร้านสะดวกซื้ออย่างละกี่ชิ้น และได้กำไรสูงสุดเท่าไร

วิธีทำจากข้อมูลที่ให้มาสามารถเขียนสรุปเป็นตารางได้ดังนี้

และสามารถนำข้อมูลมาสร้าง อสมการข้อจำกัดได้เป็น

โดยที่ต้นทุน 60x + 30y ≤ 120,000
หรือ 2x + y ≤ 4,000 ----L3
และราคาขาย 150x + 70y ≤ 360,000
หรือ 15x + 7y ≤ 36,000 ----L4
ฟังก์ชันจุดประสงค์ของกำไรหาได้จาก P = ราคาขาย - ต้นทุน
P = 150x +70y - 60x -30y หรือP = 90x + 40y

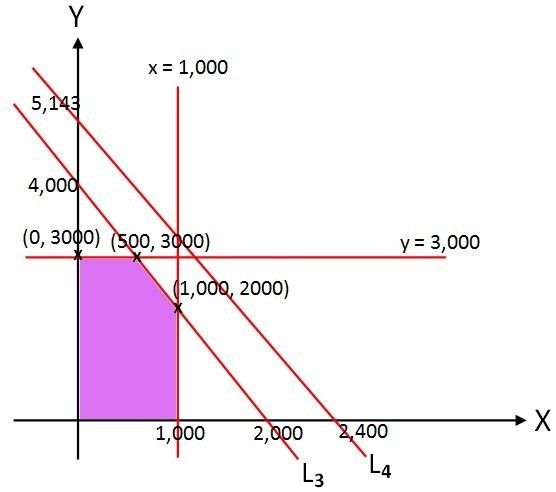
เมื่อนำจุดยอดจากกราฟมาตรวจสอบค่าของ P จะได้

ค่าสูงสุดของ P เกิดขึ้นที่จุด (1,000, 2,000)
ดังนั้นแม่ค้าควรส่งทุเรียนกวน ให้ห้างสรรพสินค้า 1,000 ชิ้น และร้านสะดวกซืือ 2,000 ชิ้น โดยได้กำไร 170,000 บาท

ตัวอย่างที่ 2บริษัทผลิตรองเท้าแห่งหนึ่ง ผลิตรองเท้าผู้ชาย และรองเท้าผู้หญิง โดยรองเท้าผู้ชายขายได้ กำไรคู่ละ 200 บาท และรองเท้าผู้หญิงได้กำไรคู่ละ 120 บาท ในแต่ละวันบริษัท จะผลิตรองเท้าผู้ชายระหว่าง 50 ถึง 100 คู่ และผลิตรองเท้าผู้หญิงระหว่าง 80 ถึง 150 คู่ ถ้าบริษัทสามารถผลิตรองเท้าสำหรับผู้ชาย และผู้หญิง รวมกัน ไม่เกิน 200 คู่ แล้วบริษัทจะได้กำไรสูงสุดกี่บาท จากการผลิตรองเท้าทั้ง 2 แบบ และต้องผลิตรองเท้าอย่างละเท่าใด

วิธีทำจากโจทย์สามารถเขียน อสมการข้อจำกัดได้ดังนี้
ทั้งนี้ ให้จำนวนรองเท้าผู้ชายที่ผลิตได้ต่อวันคือ x คู่
ให้จำนวนรองเท้าผู้หญิงที่ผลิตได้ต่อวันคือ y คู่

สามารถนำข้อมูลมาสร้างอสมการข้อจำกัดได้เป็น

x + y ≤ 200 -----L1
50 ≤ x ≤ 100 -----L2
80 ≤ y ≤ 150 -----L3
สมการจุดประสงค์ คือP = 200x + 120y

บริเวณที่สอดคล้องกับอสมการข้อจำกัดแสดงดังรูป

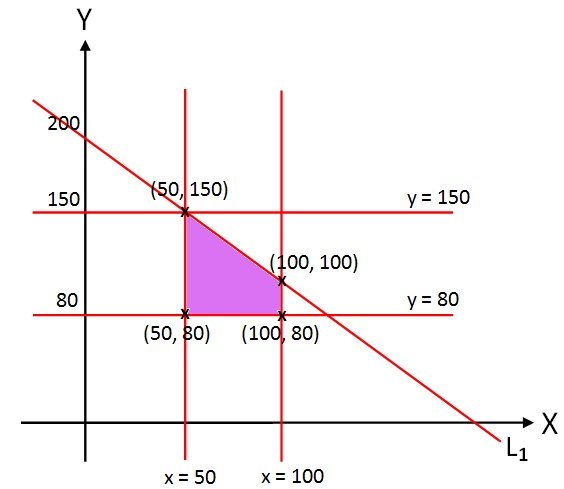
พิจารณาจุดยอดที่เกิดขึ้นจะพบว่า

เมื่อนำจุด (100, 100) และ (50, 150) มาแทนใน P = 200x + 120y
จะได้ จุด (100, 100) : P = 20,000 + 12,000 = 32,000
(50, 50) : P = 10,000 + 18,000 = 28,000

ดังนั้น บริษัทควรผลิตรองเท้าผู้ชาย และรองเท้าผู้หญิง อย่างละ 100 คู่ต่อวัน จึงจะได้กำไรสูงสุดเป็นเงิน 32,000 บาท

ตัวอย่างที่ 3มีที่ดิน 100 ไร่ ปลูกผลไม้สองชนิด คือ มังคุดและทุเรียน การปลูกมังคุดต้องลงทุน 100 บาท ต่อไร่ ส่วนการปลูกทุเรียนต้องลงทุน 160 บาทต่อไร ปลูกมังคุดให้ผลผลิต 100 กิโลกรัมต่อไร่ ปลูกทุเรียนให้ผลผลิต 40 กิโลกรับต่อไร่ ถ้ามีเงินอยู่ 14,000 บาท สำหรับลงทุนปลูกผลไม้ และมีที่เก็บผลผลิตได้ไม่เกิน 5,000 กิโลกรัม เขาควรปลูกพืชชนิดละกี่ไร่ จึงจะได้กำไรสูงสุด ถ้าขายมังคุดได้กำไร กิโลกรัมละ 6 บาท ขายทุเรียนได้กำไรกิโลกรัมละ 10 บาท

วิธีทำให้เนื้อที่ที่ใช้ปลูกมังคุด เป็น x ไร่
และเนื้อที่ที่ใช้ปลูกทุเรียน เป็น y ไร่
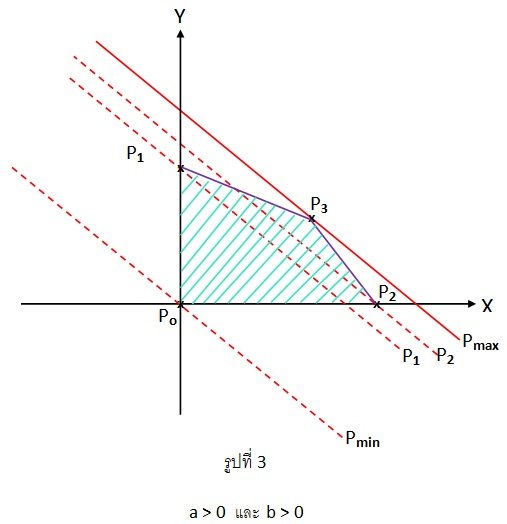
จะหาค่าสูงสุดของฟังก์ชันจุดประสงค์ P = 600x + 400y
โดยมีสมการข้อจำกัด คือ
x + y≤ 100
100x + 160y≤ 14,000
100x + 40y ≤ 5,000

เขียนกราฟของอสมการข้อจำกัดได้ดังนี้

x + y ≤ 100 ----L1
5x + 8y ≤ 700 ----L2
5x + 2y ≤ 250 ----L3

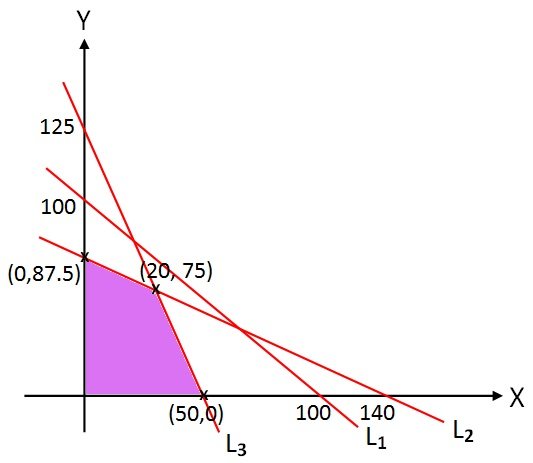
เมื่อนำจุดยอดในกราฟมาหาค่า P ได้จาก P = 600x + 400y
จะได้ (0,0) → P = 0
(0, 87.5) → P = 35,000
(20, 75) → P = 42,000
(50, 0) → P = 30,000
ค่า P สูงสุด ที่จุด (20, 75)
ดังนั้น ควรปลูกมังคุด 20 ไร่ และปลูกทุเรียน 75 ไร่ จึงจะได้กำไรสูงสุด เท่ากับ 42,000 บาท