ความสัมพันธ์แบบทวิภาค

        ท่ามกลางความหลากของธรรมชาติเราอาจจำแนกสิ่งต่างออกเป็นกลุ่ม แน่นอนว่าสมาชิกระหว่างกลุ่มนั้นอาจมีความเกี่ยวข้องกัน การจับคู่สมาชิกระหว่างกลุ่มสามารถเขียนแทนได้ด้วยคู่อันดับ (order pair) เมื่อเราทำการรวบรวมคู่อันดับของสมาชิกระหว่างกลุ่มที่เกี่ยวข้องกันในทำนองเดียวกันเราเรียกกลุ่มของคู่อันดับนี้ว่าความสัมพันธ์ กล่าวได้ว่า ความสัมพันธ์คือเซตของคู่อันดับของสิ่งสองสิ่งที่มีความเกี่ยวข้องกันในทำนองเดียวกันตัวอย่างเช่นการจัดตารางเวรทำความสะอาดจะเป็นการจับคู่นักเรียนและวันที่จะต้องทำความสะอาด ถ้านักเรียนเลขที่ 1 ของห้องจะต้องทำเวรความสะอาดทุกวันจันทร์เราสามารถเขียนในรูปคู่อันดับคือ (เลขที่1,วันจันทร์) เป็นต้น ในขณะเดียวกันหากเราพิจารณากลุ่มของนักเรียนกับกลุ่มของหน้าที่ทำความสะอาดเช่นเลขที่ 1 มีหน้าที่ ลบกระดาน เราสามารถเขียนในรูปคู่อันดับคือ (เลขที่ 1,ลบกระดาน) นอกจากนี้หากเราต้องการระบุความเกี่ยวข้องกันของนักเรียน วันที่รับผิดชอบ และหน้าที่ที่ต้องรับผิดชอบในแต่ละวันเราสามารถเขียนได้ในรูป 3 ทูเพิล ( 3-tuples ) ดังนี้ (เลขที่ 1,วันจันทร์,ลบกระดาน) เป็นต้น เมื่อเรารวบรวมทูเพิลทั้งหมดเราจะได้ความสัมพันธ์ของเลขที่ เวรที่รับผิดชอบ และหน้าที่ที่รับผิดชอบของนักเรียนแต่ละคน

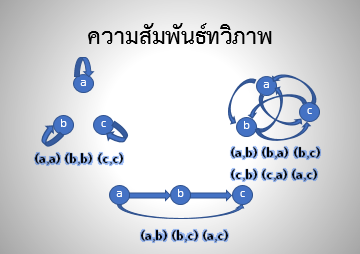
ภาพกราฟมีทิศทางแสดงความสัมพันธ์สมมูล
ที่มา วีระ ยุคุณธร

ความสัมพันธ์เชิงคณิตศาสตร์

          ความสัมพันธ์เป็นหัวข้อทางคณิตศาสตร์ที่มีบทบาทมากในการวิเคราะห์ความเกี่ยวข้องกันระหว่างสมาชิกในเซตเดียวกับหรือสมาชิกต่างเซตกัน โดยสมาชิกที่สัมพันธ์กันจะถูกเขียนในรูปของคู่อันดับ ถ้าเราให้ S เป็นเซตของนักเรียน และ C เป็นเซตของวิชา ถ้านักเรียนคนที่ s ได้ลงเรียนวิชา c นั้นคือนักเรียน s และวิชา c สัมพันธ์กันในลักษณะของการลงเรียนวิชาเขียนแทนด้วยคู่อัน (s,c) โดยที่คู่อันดับ (s,c) เป็นสมาชิกของผลคูณคาร์ทีเซียน S x C  เมื่อเรารวบรวมคู่อัน (s,c) ทั้งหมดเราจะได้เซตที่แสดงถึงความสัมพันธ์ของนักเรียนกับวิชาที่เรียน นอกจากนี้หากนักเรียน s ได้ลงเรียนวิชา c1, c2 และ c4 เราสามารถแทนด้วยคู่อันดับ

( s, { c1, c2, c4 } ) ซึ่งเป็นสมาชิกของผลคูณคาร์ทีเซียน S x P(C) โดยที่ P(C) คือเพาเวอร์เซตของเซต C

ตัวอย่างที่ 1 กำหนดให้ A = { a, b } จงหา A x P(A)

วิธีทำ พิจารณา P(A) = { { }, {a}, {b}, { a, b } } จะได้ว่า

A x P(A) = { (a, { }), (a, {a}),  (a, {b}), (a, { a, b }), (b, { }), (b, {a}),  (b, {b}), (b, { a, b }) }

ตัวอย่างที่ 2 ถ้า A และ B เป็นเซตที่มีจำนวนสมาชิกเท่ากับ 3  และ 5 ตามลำดับจำนวนความสัมพันธ์ของ A และ B ที่แตกต่างกันมีค่าเท่าใด

วิธีทำ เนื่องจาก n(A) = 3 และ n(B) = 5 จะได้ว่า n( A x B ) = 15 ความสัมพันธ์คือการเลือกหรือรวบรวมผลคูณคาร์ทีเซียนของ A และ B นั้นคือเซตย่อยของ A x B ดังนั้นจำนวนความสัมพันธ์ที่เป็นไปได้ทั้งหมดจะเท่ากับจำนวนเซตย่อยของ A x B เท่ากับ 2¹⁵

ความสัมพันธ์ทวิภาค

ความสัมพันธ์ทวิภาคเป็นการรวบรวมสมาชิกของเซต 2 เซตที่สัมพันธ์กันอาจจะเป็นเซตเดียวกันหรือต่างเซตกันก็ได้ตัวอย่างเช่น กำหนดให้ A = {1,2,3,4,5} และ B = {2,4} การจับคู่กับระหว่างเซต A และ B หรือผลคูณคาร์ทีเซียน

A x B = { (1,2), (1,4), (2,2), (2,4), (3,2), (3,4), (4,2), (4,4), (5,2), (5,4) }

จะเห็นว่ามีการจับคู่ได้ทั้งหมด 10 แบบ แต่หากเราต้องการรวบรวมสมาชิกในเซต A และ B โดยที่สมาชิกในเซต A มีค่าน้อยกว่าสมาชิกในเซต B จาก A x B จะได้คู่อันดับ (1,2), (1,4), (2,4) และ (3,4) กำหนดใด้ R เป็นความสัมพันธ์ของเซต A และ B โดยที่สมาชิกในเซต A มีค่าน้อยกว่าสมาชิกในเซต B จะได้ว่า

R = { (1,2), (1,4), (2,4), (3,4) }

ให้ R1 เป็นความสัมพันธ์ระหว่างเซต A และเซต B โดยที่สมาชิกในเซต B หารสมาชิกในเซต A ได้ลงตัว

R1 = { (2,2), (4,2), (4,4) }

ให้ R2 เป็นความสัมพันธ์บนเซต A (ระหว่างเซต A และเซต A) โดยที่สมาชิกตัวค่าแรกมีค่าน้อยกว่าค่าที่ 2

R2 = { (1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,4), (3,4), (3,5), (4,5) }

ความสัมพันธ์สมมูล

ความสัมพันธ์สมมูลเป็นความสัมพันธ์บนเซตโดยที่สอดคล้องคุณสมบัติ 3 ข้อได้แก่ การสะท้อน ความสมมาตร และ การถ่ายทอด ถ้ากำหนดให้ R เป็นความสัมพันธ์สมมูลบนเซต A แล้วจะได้ว่า

1. การสะท้อน สำหรับสมาชิก x ใด ๆ ของเซต A สมาชิก x จะต้องสัมพันธ์กับ x นั้นคือ x R x
2. ความสมมาตร สำหรับสมาชิก x และ y ใด ๆ ของเซต A ถ้า x สัมพันธ์กับ y แล้ว y จะต้องสัมพันธ์กับ x ด้วย นั้นคือ ถ้า x R y แล้ว y R x
3. การถ่ายทอด สำหรับสมาชิก x, y และ z ใด ๆ ของเซต A ถ้า x สัมพันธ์กับ y และ y สัมพันธ์กับ z แล้ว x จะต้องสัมพันธ์กับ z ด้วย นั้นคือ ถ้า x R y และ y R z แล้ว x R z

ตัวอย่างที่ 3 ความสัมพันธ์การเท่ากัน ( = ) ของจำนวนจริงเป็นความสัมพันธ์แบบสมมูลเนื่องจากสอดคล้องคุณสมบัติ 3 ข้อดังต่อไปนี้

1. จำนวนจริง x ใด ๆ x = x
2. จำนวนจริง x และ yใด ๆ ถ้า x = y แล้ว y = x
3. จำนวนจริง x, yและ yใด ๆ ถ้า x = y และ y = z แล้ว x = z

ตัวอย่างที่ 4 กำหนดความสัมพันธ์ r บนเซตจำนวนเต็มโดย x r y หมายถึง 2 หาร x – y ลงตัวเมื่อ x และ y เป็นจำนวนเต็มใด ๆ เราสามารถแสดงได้ว่า r เป็นความสัมพันธ์สมมูลดังต่อไปนี้

1. เนื่องจาก 2 หาร x – x ได้ลงตัวดังนั้น x r x
2. ให้ x r y นั้นคือ x – y หารด้วย 2 ลงตัวจะเห็นได้ว่า y - x = - ( x – y ) หารด้วย 2 ลงตัวเช่นเดียวกันดังนั้น y r x
3. ให้ x r y และ y r z จะได้ว่า x – y และ y – z หารด้วย 2 ลงตัว เรารู้ว่าผลบวกจำนวนคู่ย่อมเป็นจำนวนคู่ดังนั้น (x – y) + (y – z) = x – z จะต้องหารด้วย 2 ลงตัวทำให้ได้ว่า x r z

สอดคล้องสมบัติสามข้อของความสัมพันธ์สมมูล

แต่ น้อยกว่า ( < ) ไม่เป็นความสัมพันธ์สมมูลบนจำนวนจริงเนื่องจากขาดสมบัติการสะท้อนนั้นคือสำหรับจำนวนจริง x  ใด ๆ x < x เป็นเท็จ

แหล่งที่มา

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

กราฟความสัมพันธ์

          วิธีการหนึ่งสำหรับการนำเสนอความสัมพันธ์โดยไม่ผ่านภาษาหรือสัญลักษณ์ของคู่อันดับคือการใช้กราฟ หรือ แผนผัง โดยที่หางลูกศรแทนสมาชิกของเซตแรกที่สัมพันธ์กับสมาชิกของเซตที่สองตรงตำแหน่งหัวลูกศรในที่นี้จะนำเสนอการใช้กราฟและแผนผังแสดงความสัมพันธ์ทวิภาคแบบเต็มหน่วยซึ่งเป็นประโยชน์อย่างมากสำหรับการศึกษาความสัมพันธ์ของข้อมูล

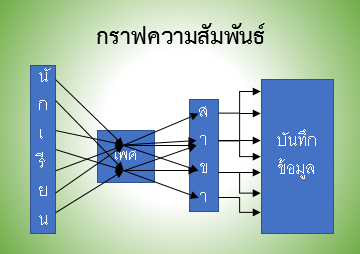
ภาพที่ 1 กราฟความสัมพันธ์กับการเก็บข้อมูล
ที่มา วีระ ยุคุณธร

กราฟความสัมพันธ์แบบเต็มหน่วย

ความสัมพันธ์แบบ one to one เป็นความสัมพันธ์ที่สมาชิกแต่ละตัวของเซตที่สองจะสัมพันธ์กับสมาชิกของเซตแรกได้เพียงตัวเดียวเท่านั้นนั้นคือถ้า y R x1 และ y R x2 แล้ว x1 = x2

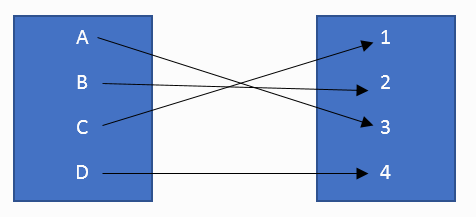
ภาพที่ 2 แผนผังความสัมพันธ์แบบ one to one

เซตความสัมพันธ์ของรูปที่ 2 เขียนแทนด้วย

{ ( A , 3 ), ( B , 2 ), ( C , 1 ), ( D , 4 ) }

จะเห็นว่าสมาชิกของเซตแรกสัมพันธ์กับสมาชิกเซตที่ 2 ตัวใดตัวหนึ่งตัวอย่างเช่นนักเรียนหนึ่งคนจะมีรหัสนักเรียนแค่รหัสเดียวซึ่งไม่ซ้ำกับนักเรียนคนอื่น

ความสัมพันธ์แบบ one to many เป็นความสัมพันธ์ที่สมาชิกของเซตที่แรกมีความสัมพันธ์กับสมาชิกของเซตที่สองได้มากกว่า 1 ตัว

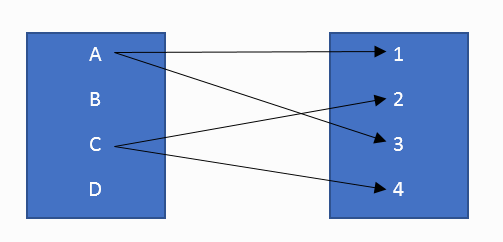
ภาพที่ 3 ความสัมพันธ์แบบ one to many

เซตความสัมพันธ์ของรูปที่ 3 เขียนแทนด้วย

{ ( A , 1 ), ( A , 3 ), ( C, 2 ), ( C , 4 ) }

จะเห็นว่ามีสมาชิกของเซตแรกสัมพันธ์กับสมาชิกเซตที่ 2 อย่างน้อย 1 ตัว ตัวอย่างของความสัมพันธ์ของข้อมูลที่เป็นแบบ one to many อาทิในการแข่งขันกีฬาสี เซตแรกเป็นเซตของนักเรียนและเซตที่ 2 เป็นเซตของประเภทกีฬาโดยแต่ละสีส่งนักกีฬาได้เพียงคนเดียว แต่นักเรียนแต่ละคนสามารถเล่นกีฬาได้มากกว่า 1 ประเภท

ความสัมพันธ์แบบ many to one เป็นความสัมพันธ์ที่สมาชิกของเซตที่แรกมีความสัมพันธ์กับสมาชิกของเซตที่สองได้มากกว่า 1 ตัว

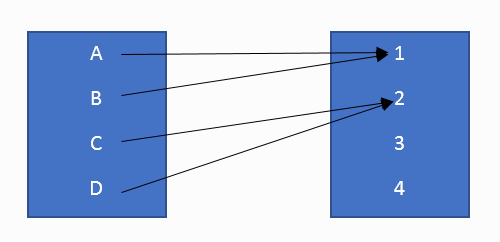
ภาพที่ 4 แผนผังความสัมพันธ์แบบ many to one

เซตความสัมพันธ์ของรูปที่ 4 เขียนแทนด้วย

{ ( A , 1 ), ( B , 1 ), ( C , 2 ), ( D , 2 ) }

จะเห็นว่ามีสมาชิกของเซตที่ 2 สัมพันธ์กับสมาชิกเซตของแรกอย่างน้อย 1 ตัว ข้อมูลในชีวิตประจำวันที่มีความสัมพันธ์แบบ many to one ได้แก่ ความสัมพันธ์ของข้อมูลนักเรียนในห้องและข้อมูลเพศ

ความสัมพันธ์แบบ many to many

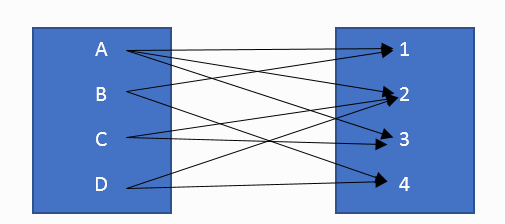
ภาพที่ 5 แผนผังความสัมพันธ์แบบ many to many

เซตความสัมพันธ์ของรูปที่ 5 เขียนแทนด้วย

{ ( A , 1 ), ( A , 2 ), ( A , 3 ), ( B , 1 ), ( B , 4 ), ( C , 2 ), ( C , 3 ), ( D , 2 ), ( D , 4 ) }

จะเห็นว่ามีสมาชิกของเซตแรกสัมพันธ์กับสมาชิกเซตที่ 2 อย่างน้อย 1 ตัวและสมาชิกของเซตที่ 2 สัมพันธ์กับสมาชิกของเซตที่ 1 อย่างน้อย 1 ตัวเช่นเดียวกัน ตัวอย่างของความสัมพันธ์ของข้อมูลที่เป็นแบบ one to many อาทินักเรียนหนึ่งคนอาจมีความถนัดในการเรียนมากกว่า 1 วิชาในขณะเดียวกันแต่ละวิชามีนักเรียนที่ถนัดมากกว่า 1 คนเป็นต้น

ความสัมพันธ์กับฟังก์ชัน

จากความสัมพันธ์ทั้ง 4 รูปแบบข้างต้นอย่างเราต้องการออกแบบการทำงานโดยที่อินพุตที่ถูกป้อนเข้าสู่ระบบจะให้เอาท์พุตเพียงแค่เอาท์พุตเดียวเราเรียกการทำงานแบบนี้ว่าฟังก์ชัน เมื่อย้อนกลับไปพิจารณารูปแบบความสัมพันธ์ข้างต้นแล้วจะพบว่าความสัมพันธ์แบบ one to one และ many to one เท่านั้นที่เป็นฟังก์ชัน เราให้นิยามของฟังก์ชัน f ที่เป็นความสัมพันธ์ของเซต A และ B โดยผ่านเงื่อนไขสองข้อต่อไปนี้

1. Existence การมีของเอาท์พุตของแต่ละอินพุต สำหรับ x ใดๆที่เป็นสมาชิกของ A จะมี y ที่เป็นสมาชิกของ B ซึ่ง ( x , y ) เป็นสมาชิกของฟังก์ชัน
2. Uniqueness การมีอยู่เพียงหนึ่งเดียวของเอาท์พุตสำหรับแต่ละอินพุตนั้นคือ สำหรับ x ใดๆที่เป็นสมาชิกของ A ถ้า ( x , y1 ) และ ( x , y2 ) เป็นสมาชิกของฟังก์ชันแล้ว y1 = y2

เราเรียกเซต A ว่าโดเมนของฟังก์ชัน เรียก B ว่าโคโดเมนของฟังก์ชัน และ เรียก f(A) ว่าเรนจ์ของฟังก์ชัน

ตัวอย่างที่ 1 จงพิจารณาว่าความสัมพันธ์  { ( 1 , a ), ( 1 , b ), ( 2 , c ), ( 3 , a ) } เป็นฟังก์ชันหรือไม่

วิธีทำ เนื่องจากอินพุต 1 ให้เอาท์พุต a และ b จะเห็นว่ามีเอาท์พุตมากกว่า 2 ดังนั้นความสัมพันธ์ที่กำหนดให้ไม่เป็นฟังก์ชัน

 ตัวอย่างที่ 2 จงพิจารณาว่าความสัมพันธ์  { ( 1 , a ), ( 2 , c ), ( 3 , a ) } จงหาโดเมนและเรนจ์ของฟังก์ชัน

วิธีทำ โดเมน = { 1, 2, 3 } และ เรนจ์ = { a, c }

ตัวอย่างที่ 3 กำหนดฟังก์ชัน { ( x , y ): x และ y เป็นจำนวนจริงใด ๆ ซึ่ง y - 2x =1 } จงหาโดเมนและเรจน์ของฟังก์ชัน

วิธีทำ เนื่องจากโดเมนของฟังก์ชันเป็นจำนวนจริงใด ๆ สำหรับเรนจ์ของฟังก์ชันพิจารณา y – 2x = 1 จะเห็นได้ว่า y = 2x + 1 เนื่องจาก x เป็นจำนวนจริงใด ๆ แล้ว 2x + 1 เป็นจำนวนจริงด้วยเช่นกันดังนั้นเรนจ์ของฟังก์ชันคือจำนวนจริง

ตัวอย่างที่ 4  กำหนดฟังก์ชัน { ( x , y ): x และ y เป็นจำนวนเต็มบวก ซึ่ง y - 2x =1 } จงหาโดเมนและเรนจ์ของฟังก์ชัน

วิธีทำ จากคุณสมบัติของ x พบว่า x เป็นจำนวนเต็มบวกซึ่งเป็นโดเมนของฟังก์ชันก์ พิจารณาเรนจ์ของฟังก์ชันจาก y - 2x =1 จะได้ว่า y = 2x + 1 เนื่องจาก 2x เป็นจำนวนเต็มคู่ ดังนั้น 2x + 1 เป็นจำนวนเต็มคี่ สรุปได้ว่าเรนจ์ของฟังก์ชันคือเซตของจำนวนเต็มคี่

แหล่งที่มา

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.

ความสัมพันธ์ประกอบ

          หากเรามีความสัมพันธ์ระหว่างกลุ่มสองกลุ่ม และต้องการเชื่อมโยงความสัมพันธ์กับกลุ่มที่สามโดยที่สมาชิกของกลุ่มที่สามมีความสัมพันธ์กับกลุ่มใดกลุ่มหนึ่งในสองกลุ่มข้างต้น เราสามารถสร้างความสัมพันธ์ใหม่ที่ถ่ายถอดความสัมพันธ์จากกลุ่มที่ 1 ไปยังกลุ่มที่ 2 และจากกลุ่มที่ 2 ไปยังกลุ่มที่ 3 เราเรียกความสัมพันธ์นี้ว่าความสัมพันธ์ประกอบซึ่งแสดงความสัมพันธ์ของสมาชิกในกลุ่มที่ 1 และสมาชิกในกลุ่มที่ 3

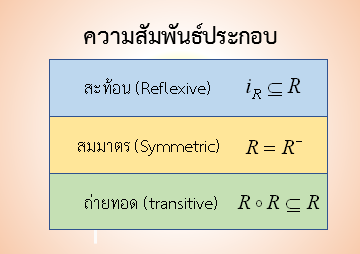
ภาพที่ 1 ทฤษฎีบทตรวจสอบความสัมพันธ์สมมูล
ที่มา วีระ ยุคุณธร

ความสัมพันธ์ประกอบ

          กำหนดให้ S เป็นความสัมพันธ์ระหว่างเซต A และ B และ R เป็นความสัมพันธ์ระหว่างเซต B และ เซต C  ถ้าเราเลือกสมาชิกในเซต B ที่มีสัมพันธ์กับเซต A และ เซต C แล้วเราจะสามารถเชื่อมโยงความสัมพันธ์ระหว่างเซต A และ C ด้วยความสัมพันธ์ประกอบเขียนแทนด้วย RoS

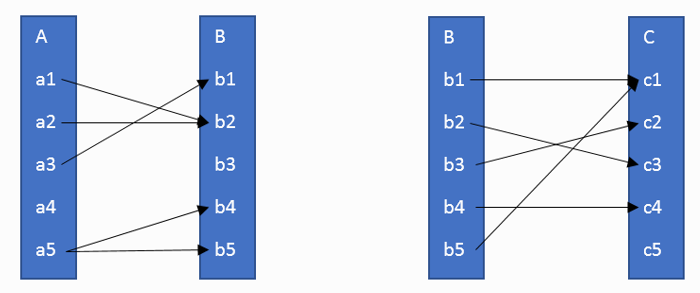
รูปที่ 2 แผนผังแสดงความสัมพันธ์ S (ซ้าย) และ ความสัมพันธ์ R (ขวา)
ที่มา วีระ ยุคุณธร

จากรูปที่ 2 เราสามารถเขียนความสัมพันธ์ในรูปของเซตของคู่อันดับได้ดังนี้

            S = { (a1,b2), (a2,b2), (a3,b1), (a5,b4), (a5,b5) } และ   R = { (b1,c1), (b2,c3), (b3,c2), (b4,c4), (b5,c1) }

เมื่อนำความสัมพันธ์ทั้งสองมาประกอบกันจะพบว่าสมาชิกของเซต B ที่มีความสัมพันธ์กับเซต A และ C ได้แก่ b1, b2, b4 และ b5

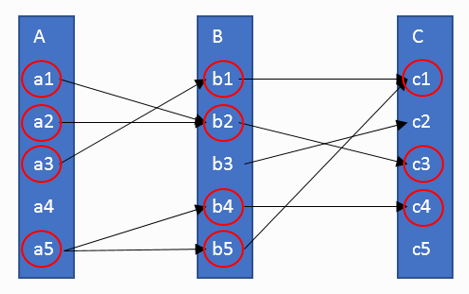
รูปที่ 3 แผนผังแสดงความสัมพันธ์ RoS
ที่มา วีระ ยุคุณธร

     ในรูปที่ 3 จะเห็นว่าเซต B ที่สัมพันธ์กับเซต A และ C ประกอบด้วย b1, b2, b4 และ b5 ซึ่ง 

              b1 สัมพันธ์แบบ S กับ a3 ( a3 S b1 ) และสัมพันธ์แบบ R กับ c1 ( b1 R c1 ) จะได้ว่า a3 RoS c1

              b2 สัมพันธ์กับ a1 และ a2 แบบ S ( a1 S b2, a2 S b2 ) และ b2 สัมพันธ์แบบ R กับ c3 (b2 R c3)  

        จะได้ว่า a1 RoS c3 และ a2 RoS c3

              b4 สัมพันธ์แบบ S กับ a5 ( a5 S b4 ) และสัมพันธ์แบบ R กับ c4 ( b4 R c4 ) จะได้ว่า a5 RoS c4

              b5 สัมพันธ์แบบ S กับ a5 ( a5 S b5 ) และสัมพันธ์แบบ R กับ c1 ( b5 R c1 ) จะได้ว่า a5 RoS c1

       ผลพิจารณาข้างต้นเราได้ความสัมพันธ์ประกอบของ S และ R ดังนี้  RoS = { (a3,c1), (b2,c3), (a5,c4), (a5,c1) }

ตัวอย่างการคำนวณ

กำหนดให้ A = { (ก,ก), (ก,ค), (ข,ค), (ข,ง), (ค,ก), (ค,ง), (ค,จ) } และ B = { (ก,ก), (ก,ข), (ข,ก), (ง,ข), (จ,ก), (จ,ข) } จงหา BoA

        พิจารณาความสัมพันธ์ A จะได้ กAก กAค ขAค ขAง คAก คAง คAจ และความสัมพันธ์ B จะได้ กBก กฺBข ขBก งBข จBก จBข

        จาก กAกฺ จะเห็นว่า กAกฺBก, กAกฺBข => กBoAก, กBoAข

        จาก ขAง จะเห็นว่า ขAงBข => ขBoAข

        จาก คAก จะเห็นว่า คAกฺBก, คAกฺBข => คBoAก, คBoAข

        จาก คAง จะเห็นว่า คAงBข => คBoAข

        จาก คAจ จะเห็นว่า คAจBก, คAจBข => คBoAก, คBoAข

        ดังนั้น BoA = { (ก,ก), (ก,ข), (ข,ข), (ค,ก), (ค,ข) }

ความสัมพันธ์เอกลักษณ์และความสัมพันธ์ผกผัน

        คุณสมบัติเอกลักษณ์ของการดำเนินการทางคณิตศาสตร์กำหนดไว้ว่าเมื่อเรานำเอกลักษณ์ไปดำเนินการกับสมาชิกในเซตใด ๆแล้วผลการดำเนินการทำให้ได้สมาชิกค่าเดิมเช่น เอกลักษณ์การบวกของจำนวนจริง เมื่อเรานำเอกลักษณ์การบวกไปบวกกับจำนวนจริงใดๆ แล้วจะได้จำนวนเดิมเช่นถ้าให้ a เป็นจำนวนจริงใด ๆและ e เป็นเอกลักษณ์การบวกแล้ว a + e = a = e + a จะเห็นได้โดยง่ายว่า e = 0 สรุปได้ว่า ศูนย์เป็นเอกลักษณ์การบวก ในทำนองเดียวกันเราจะพบว่า 1 คือเอกลักษณ์การคูณของจำนวนจริง นอกจากนี้สังเกตได้ว่า เซตว่างเป็นเอกลักษณ์การยูเนียน ยูนิเวอร์สเป็นเอกลักษณ์การผนวกของเซต ข้อยังแย้งเป็นเอกลักษณ์การดำเนินการเลือกทางตรรกศาสตร์ (หรือ) และสัจนิรันดร์เป็นเอกลักษณ์การดำเนินรวมทางตรรกศาสตร์ (และ)

        ความสัมพันธ์เอกลักษณ์จึงเป็นความสัมพันธ์ที่ถูกนิยามในทำนองเดียวกันกล่าวคือ ถ้า iA เป็นเอกลักษณ์ความสัมพันธ์บนเซต A แล้ว a iA a เมื่อ a เป็นสมาชิกใดของเซต A ตัวอย่างเข่น iA = { (a,a), (b,b), (c,c) } เมื่อ A = { a, b, c }

        เมื่อระบบมีเอกลักษณ์ระบบอาจจะมีตัวผกผัน เช่นตัวผกผันการบวกคือจำนวนที่ทำให้ผลบวกของจำนวนจริงใดๆ กับตัวผกผันของจำนวนนั้นเป็นเอกลักษณ์การบวก ถ้ากำหนดให้ a เป็นจำนวนจริงใด ๆ แล้ว –a เป็นตัวผกผันของ a ซึ่ง a + (-a) = 0 สำหรับการคูณเมื่อพิจารณาจำนวนจริงที่ไม่ใช่ 0 แล้วเราจะได้ว่าตัวผกผันการคูณของ a คือ 1/a เพราะว่า a x (1/a) = 1 ในการศึกษาตัวผกผันของความสัมพันธ์ ถ้าเรากำหนดให้ A = { a, b, c, d} และ B = { x, y, z } โดยที่ความสัมพันธ์ R ระหว่างเซต A และ เซต B กำหนดไว้ดังนี้

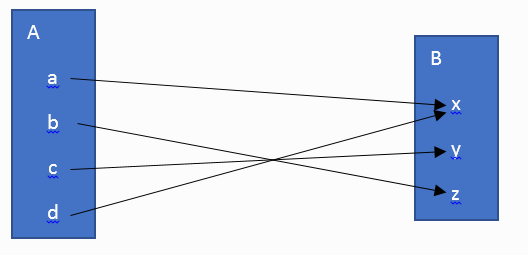
ภาพที่ 4 แสดงความสัมพันธ์ R ระหว่างเซต A และ B

       เขียนความสัมพันธ์ในรูปของเซตได้ดังนี้ R = { (a,x), (b,z), (c,y), (d,x) } สมมติให้ R^- เป็นความสัมพันธ์ผกผันของความสัมพันธ์ R นั้นหมายความว่า R^- จะต้องเป็นความสัมพันธ์ระหว่างเซต B และ เซต A โดยที่ R^-oR เป็นความสัมพันธ์เอกลักษณ์

       R^-oR= { (a,a), (b,b), (c,c), (d,d) }

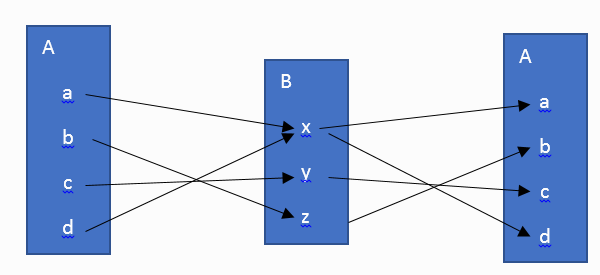
ภาพที่ 5 ความสัมพันธ์ประกอบของ R^-1oR

     จะเห็นว่า R^- = { (x,a), (y,c), (z,b), (x,d) } นิยามความสัมพันธ์ผกผันได้ดังนี้

     R^- = { (y,x), เมื่อ (x,y) เป็นความสัมพันธ์ R

ตัวอย่างคำนวณ

      กำหนด R = { (a,b), (a,c), (b,b), (b,d) (c,d) (d,b) }  จงหา R^-

      R^-= { (b,a), (c,a), (b,b), (d,b), (d,c), (b,d) }

แหล่งที่มา

Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.