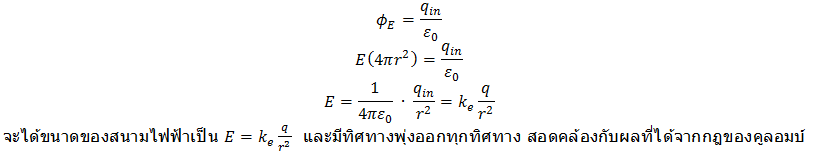เบนจามิน แฟรงคลิน (Benjamin Franklin, 1706-1790) พบว่าการขัดสีวัตถุด้วยผ้าขนสัตว์  ทําให้เกิดประจุบนวัตถุ และได้ทดลองนําแท่งแก้วและยางที่มีประจุจากการขัดสีไปวางใกล้แท่งยาง  ที่แขวนไว้ด้วยเชือกพบว่าแท่งแก้วออกแรงดูดแต่แท่งยางออกแรงผลัก แสดงว่าประจุที่เกิดในวัสดุ  ชนิดเดียวกันจะผลักกันและประจุในวัสดุต่างชนิดจะดูดกัน ประจุทําให้เกิดแรงกระทํากับวัตถุได้ 2  แบบ จึงคิดว่าควรมีประจุ 2 ชนิดโดยเรียกประจุชนิดหนึ่งว่าประจุบวก (positive charge) และ ประจุอีกชนิดว่าประจุลบ (negative charge) แรงที่เกิดจากประจุต่างชนิดกันจะดูดกันและประจุ ชนิดเดียวกันจะผลักกัน ในภายหลังได้มีการทดลองและศึกษาคุณสมบัติของประจุทั้งสอง

คุณสมบัติของประจุ

อนุภาคประจุบวกเรียกว่าโปรตอน (proton, p) มีประจุเท่ากับ +e อนุภาคประจุลบเรียกว่าอิเล็กตรอน (electron, e ) มีประจุเท่ากับ -e การขัดสีทําให้เกิดประจุบนวัตถุเนื่องจากการแลกเปลี่ยนประจุระหว่างวัตถุที่ขัดสีกัน ภายหลังทราบว่าประจุลบมีมวลน้อยกว่าประจุบวกมาก ดังนั้นการแลกเปลี่ยนประจุเกิดขึ้นเพราะประจุลบเคลื่อนที่โดยจํานวนประจุที่เกิดขึ้นเป็นจํานวนเท่า (จํานวนเต็ม) ของประจุอิเล็กตรอน วัสดุที่เป็นกลางทางไฟฟ้าจะมีจํานวน อนุภาคประจุบวกเท่ากับประจุลบ ถ้าเอาอิเล็กตรอน n ตัวออกจากวัสดุจะทําให้วัสดุมีประจุสุทธิ เป็นบวกเท่ากับ +ne ถ้าให้อิเล็กตรอน n ตัวกับวัสดุจะทําให้มีประจุสุทธิเป็น -ne

วัสดุตัวนําและฉนวน

วัสดุโดยทั่วไปจะเป็นกลางทางไฟฟ้าคือมีประจุบวกเท่ากับประจุลบ และมีอิเล็กตรอนจํานวนมหาศาลในเนื้อวัสดุ ฉนวน เช่น แก้ว และ ยาง เป็นวัสดุที่ไม่นําไฟฟ้า เมื่อนําไปขัดถูจะเกิดประจุบริเวณที่มีการเสียดสี ประจุที่เกิดขึ้นจะไม่สามารถเคลื่อนที่ไปยังส่วนอื่น ๆ ของวัสดุได้ ตัวนํา เช่น ทองแดง อลูมิเนียม และ เงิน เมื่อมีประจุเกิดขึ้นในส่วนหนึ่งของวัสดุ ประจุจะกระจายตัวออกไปทั่วทั้งพื้นผิวของวัสดุเพราะอิเล็กตรอนสามารถเคลื่อนที่ได้อย่างอิสระที่ผิวตัวนํา

กฎของคูลอมบ์ (Coulomb’s Law)

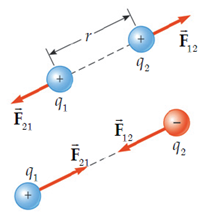
ชาร์ล คูลอมบ์ (Charles Coulomb, 1736-1806) ศึกษาขนาดของแรงระหว่างประจุไฟฟ้าพบว่าแรงที่เกิดขึ้นระหว่างประจุจะมีทิศตามแนวเส้นตรงที่เชื่อมระหว่างประจุนั้น ถ้าประจุเป็นชนิดเดียวกันจะเป็นแรงผลักและประจุต่างชนิดเป็นแรงดูด ขนาดของแรงลดลงตามระยะห่างกำลังสอง และขึ้นกับปริมาณประจุ

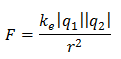
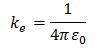
ตัวอย่างแรงระหว่างอนุภาคประจุ อนุภาค A มีประจุ +2.0 μC และอนุภาค B มีประจุ +6.0 μC อยู่ห่างกันเป็นระยะ 1.0 m  แรงที่อนุภาค B กระทำต่ออนุภาค A มีขนาดเท่าใดและมีทิศใดใช้กฎของคูลอมบ์หาแรงระหว่างอนุภาคประจุ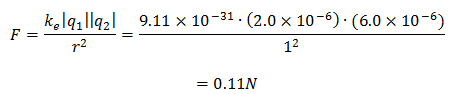มีแรงกระทำขนาด 0.11N มีทิศตามแนวเส้นตรงที่เชื่อมระหว่างอนุภาค A และ B ทำให้อนุภาคA พุ่งออกจากอนุภาค Bสนามไฟฟ้า (Electric Field)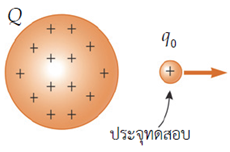

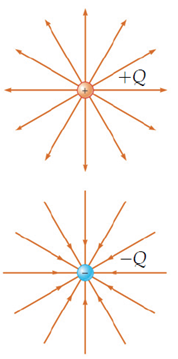
ถ้าอนุภาค q เป็นประจุบวก แรงที่เกิดขึ้นจะมีทิศเดียวกับทิศของสนามไฟฟ้า แต่ถ้า q เป็นประจุ ลบ แรงจะมีทิศตรงข้ามกับทิศของสนามไฟฟ้า
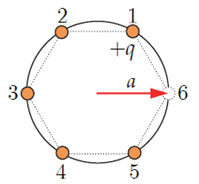
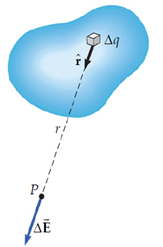
ตัวอย่างสนามไฟฟ้าเนื่องจากอนุภาคประจุจำนวนมาก อนุภาคประจุ +q จำนวน 6 ตัว ถูกตรึงให้ห่างกันอย่างสม่ำเสมอบนโครงวงกลมรัศมี a ถ้านำ อนุภาคออกจากระบบหนึ่งตัว สนามไฟฟ้าที่จุดศูนย์กลางวงกลมจะมีขนาดเท่าใดและมีทิศใด สนามไฟฟ้าจากประจุที่กระจายตัวต่อเนื่องวัตถุที่มีการกระจายตัวต่อเนื่องเป็นรูปทรงนั้นประกอบถือว่าประกอบด้วยอนุภาคจุดประจุ จำนวนมาก สนามไฟฟ้าเนื่องจากวัตถุหาได้โดยพิจารณาอิทธิพลของสนามที่เกิดจากแต่ละอนุภาค  (จุดเล็ก ๆ) ที่รวมเป็นวัตถุ ซึ่งสนามไฟฟ้ารวมเท่ากับผลรวมของแต่ละจุดเล็ก ๆ บนวัตถุทั้งชิ้น หลักง่าย ๆ ในการพิจารณาคือ สมมติว่าวัตถุนั้นประกอบขึ้นจากหน่วยเล็ก ๆ (อาจจินตนาการว่าเป็นเม็ดทราย) จำนวนมาก (ให้เป็น i หน่วย) ซึ่งแต่ละหน่วยมีประจุเป็น แน่นอนว่าถ้ารวมประจุจากทุกหน่วยเข้าด้วยกันจะต้องได้ขนาดประจุเท่ากับประจุรวม (ให้เป็น Q ) ดังนั้นสนามไฟฟ้าจากหนึ่งหน่วยเล็ก ๆ จะเท่ากับ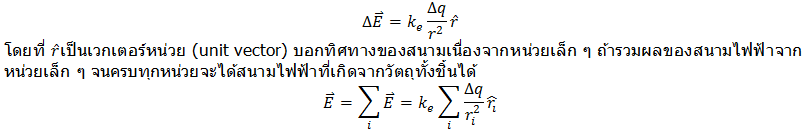

จากสมการข้างต้นจะเห็นว่าตัวแปรของการอินทิเกรตคือการรวมอิทธิพลของ dq ที่ระยะห่าง r จากหน่วยย่อยไปยังจุดที่จะหาค่าสนามไฟฟ้า ซึ่งหน่วยของประจุและระยะทางเป็นหน่วยที่แตกต่างกัน การอินทิเกรตนี้จะง่ายขึ้นถ้าปรับหน่วยของตัวแปรทั้งสองให้สอดคล้องกันและขึ้นกับลักษณะรูปทรงของวัตถุ การหาสนามไฟฟ้าจากประจุที่กระจายตัวต่อเนื่องจะง่ายขึ้นถ้าหาขนาดของประจุที่จุดเล็ก ๆ นั้นจากความหนาแน่นของประจุ ความหนาแน่นประจุ (Charge Density)ตัวอย่างสนามไฟฟ้าเนื่องจากเส้นลวดที่มีประจุกระจายตัวอย่างสม่ำเสมอลวดยาว  มีประจุสุทธิ Q กระจายตัวอย่างสม่ำเสมอ สนามไฟฟ้าที่จุด P ซึ่งห่างจากปลายลวด ตามแนวเส้นลวดเป็นระยะ a มีขนาดและทิศทางอย่างไร

ตัวอย่างสนามไฟฟ้าเนื่องจากลวดวงกลมที่มีประจุกระจายตัวอย่างสม่ำเสมอเส้นลวดดัดเป็นวงกลมรัศมี a มีประจุสุทธิ Q กระจายตัวอย่างสม่ำเสมอ สนามไฟฟ้าที่จุด P ซึ่งห่างจากจุดศูนย์กลางในแนวตั้งฉากกับระนาบของวงกลมเป็นระยะ x มีขนาดและทิศทางอย่างไรหาสนามไฟฟ้าเนื่องจากส่วนย่อยที่อยู่บนเส้นลวด แล้วรวมผลจากส่วนย่อยตลอดเส้นรอบวงกลม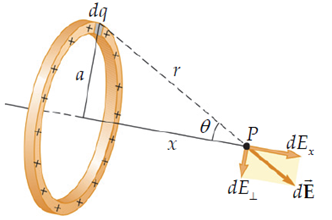

เส้นสนามไฟฟ้า (Electric Field Lines)เส้นสนามไฟฟ้าเป็นเส้นที่ใช้แสดงทิศทางของสนามไฟฟ้า สนามไฟฟ้าจะมีทิศในแนวเส้นสัมผัส กับเส้นสนาม จำนวนเส้นสนามที่ทะลุผ่านพื้นที่ที่ตั้งฉากกับเส้นสนามแปรผันตรงกับขนาด หรือความเข้มของสนามไฟฟ้าในบริเวณนั้น บริเวณที่มีเส้นสนามอยู่ชิดกันมากจะมีค่าสนามไฟฟ้าสูง ข้อควรระวังคือเส้นสนามบอกทิศทางของแรงที่กระทำกับประจุทดสอบแต่เส้นสนามไม่ใช่เส้นทางการเคลื่อนที่ของประจุฟลักซ์ไฟฟ้า (Electric Flux)ฟลักซ์ไฟฟ้าแปรผันตรงกับเส้นสนามไฟฟ้าที่ทะลุผ่านพื้นที่สมมติหนึ่ง ๆ ทั้งนี้จะคิดเฉพาะองค์ประกอบของสนามไฟฟ้าที่ตั้งฉากกับพื้นที่สมมติ ( A) ถ้าสนามไฟฟ้าที่ผ่านพื้นที่มีค่าสม่ำเสมอ (E) ฟลักซ์ไฟฟ้าที่ผ่านพื้นที่นั้นจะเท่ากับถ้าเส้นสนามที่ทะลุผ่านพื้นที่นั้นไม่ตั้งฉากกับพื้นผิวและทำมุมค่าหนึ่งกับ แนวที่ตั้งฉากกับพื้นผิว หรือ เวกเตอร์ปกติ (normal vector) สำหรับพื้นผิวใดใดเวกเตอร์ปกติจะตั้งฉากกับพื้นผิว และมีทิศพุ่งออกจากพื้นผิวเสมอ ฟลักซ์จะมีค่าสูงสุดเมื่อพื้นผิวทำมุมตั้งฉากกับเส้นสนาม (หรือเวกเตอร์ปกติอยู่ในทิศทางเดียวกับสนามไฟฟ้า) และจะมีค่าน้อยที่สุดเป็นศูนย์ เมื่อพื้นผิวอยู่ในแนวเดียวกับเส้นสนาม (หรือเวกเตอร์ปกติตั้งฉากกับทิศของสนามไฟฟ้า)ฟลักซ์ของปริมาณใด ๆ เปรียบเหมือนกับปริมาณนั้น ๆ ที่ตกกระทบพื้นที่หนึ่ง ๆ ยกตัวอย่างเช่น ถ้านำกระดาษแผ่นหนึ่งใช้เป็นร่มบังแสงแดด ถ้าให้แผ่นกระดาษตั้งฉากกับทิศทางของแสงแดด เงาที่เกิดจากกระดาษเปรียบได้กับฟลักซ์ของแสงแดดที่ตกกระทบพื้นที่ของกระดาษ ถ้าปรับเปลี่ยนทิศทางของเส้นปกติของแผ่นกระดาษเป็นมุมต่าง ๆ เงาของกระดาษจะมีขนาดเล็กลง และถ้าแนวกระดาษอยู่ในแนวเดียวกับแสงแดด เงาของกระดาษจะเล็กมากเทียบได้กับฟลักซ์ที่เป็นศูนย์ฟลักซ์ของปริมาณใด ๆ เปรียบเหมือนกับปริมาณนั้น ๆ ที่ตกกระทบพื้นที่หนึ่ง ๆ ยกตัวอย่างเช่น ถ้านำกระดาษแผ่นหนึ่งใช้เป็นร่มบังแสงแดด ถ้าให้แผ่นกระดาษตั้งฉากกับทิศทางของแสงแดด เงาที่เกิดจากกระดาษเปรียบได้กับฟลักซ์ของแสงแดดที่ตกกระทบพื้นที่ของกระดาษ ถ้าปรับเปลี่ยนทิศทางของเส้นปกติของแผ่นกระดาษเป็นมุมต่าง ๆ เงาของกระดาษจะมีขนาดเล็กลง และถ้าแนวกระดาษอยู่ในแนวเดียวกับแสงแดด เงาของกระดาษจะเล็กมากเทียบได้กับฟลักซ์ที่เป็นศูนย์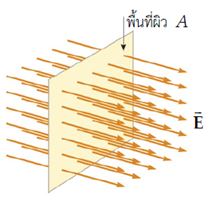ตัวอย่างฟลักซ์ไฟฟ้าจากจุดประจุ หาฟลักซ์ไฟฟ้าที่ทะลุผ่านทรงกลมซึ่งมีรัศมี 1.00m และมีประจุขนาด +1.00 μC อยู่ที่ศูนย์กลางพิจารณาขนาดและทิศทางของสนามไฟฟ้าที่ผ่านพื้นผิวทรงกลม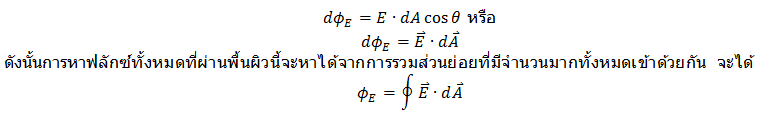เครื่องหมายของฟลักซ์ฟลักซ์เป็นผลคูณเชิงสเกลาร์ระหว่างสนามกับพื้นที่ ขนาดของสนามและพื้นที่จะมีค่าเป็นบวกเสมอ ดังนั้นเครื่องหมายของฟลักซ์จะได้จากการคูณเชิงสเกลาร์ (dot product) ของทิศทางระหว่างสนามกับเวกเตอร์ปกติของพื้นผิว เมื่อพิจารณาวัตถุที่เป็นรูปร่างใดใดและอยู่ในบริเวณที่มีสนาม จะพิจารณาผลลัพธ์เครื่องหมายของฟลักซ์ได้ 3 กรณีแยกตามมุมระหว่างเวกเตอร์ปกติของพื้นผิวกับทิศของสนามไฟฟ้า โดยฟลักซ์จะมีเครื่องหมายสอดคล้องกับทิศทางของสนามไฟฟ้าว่าพุ่งออกหรือสัมผัสกับแนวพื้นผิวหรือพุ่งเข้า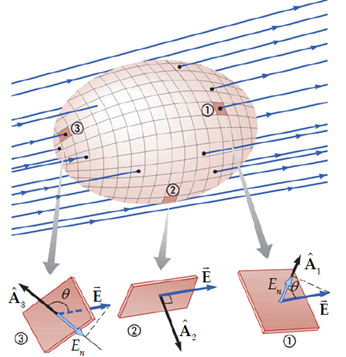ถ้าสร้างพื้นผิวปิดสมมติล้อมรอบอนุภาคประจุหนึ่ง จะพบว่าถ้าประจุนั้นเป็นประจุบวกสนามไฟฟ้าที่เกิดขึ้นจะมีทิศพุ่งออกจากผิวปิดทำให้ฟลักซ์เป็นบวก ถ้าเป็นประจุลบสนามไฟฟ้ามีทิศพุ่งเข้าหาประจุและมีทิศพุ่งเข้าผิวปิดด้วย ทำให้ฟลักซ์มีค่าเป็นลบ แสดงว่าเครื่องหมายของฟลักซ์สอดคล้องกับชนิดของประจุสุทธิที่อยู่ภายในผิวปิดนั้นตัวอย่างหาฟลักซ์ไฟฟ้าที่ทะลุผ่านลูกบาศก์หาฟลักซ์ไฟฟ้าที่ทะลุผ่านลูกบาศก์ซึ่งมีความยาวแต่ละด้านเป็น  และวางอยู่ในบริเวณที่มีสนามไฟฟ้าสม่ำเสมอไปทางแกน +x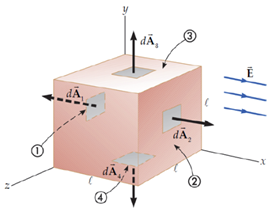
คำนวณฟลักซ์โดยแบ่งผิวปิดออกเป็นพื้นผิวย่อยเนื่องจากสนามไฟฟ้ามีขนาดสม่ำเสมอและมีทิศอยู่ในแนวขอบลูกบาศก์พอดี สามารถแบ่งผิวปิดเป็น 6 ด้านเพื่อแยกคำนวณฟลักซ์ของกล่องลูกบาศก์ได้ เวกเตอร์ปกติของพื้นผิวทั้ง 6 ด้านจะมีทิศตั้งฉากกับกล่องดังรูป จะเห็นว่ามีด้าน 4 ด้านที่พื้นผิวอยู่ในแนวเดียวกับสนามไฟฟ้า จะได้

ที่น่าสังเกตคือกฎของเกาส์แสดงความสัมพันธ์ระหว่างประจุที่อยู่ภายในผิวปิดกับฟลักซ์ไฟฟ้าที่ผ่านผิวปิดซึ่งผิวปิดจะมีรูปร่างแบบใดก็ได้ ดังนั้นไม่ว่าผิวปิดจะมีรูปแบบใดถ้าเราทำการคำนวณฟลักซ์ไฟฟ้าของผิวปิดนั้นที่บรรจุประจุเช่นเดียวกันฟลักซ์ไฟฟ้าจะไม่ขึ้นกับรูปร่างและขนาดของผิดปิดเลย ถ้าผิวปิดไม่มีประจุบรรจุอยู่ภายใน หรือผลรวมของประจุสุทธิที่อยู่ภายในผิวปิดเป็นศูนย์ฟลักซ์ที่ผ่านผิวปิดนั้นย่อมเป็นศูนย์ แต่ไม่ได้หมายความว่าบริเวณนั้นไม่มีสนามไฟฟ้า

ตัวอย่างใช้กฎของเกาส์หาสนามไฟฟ้าเนื่องจากจุดประจุสร้างผิวปิดสมมติแล้วคำนวณฟลักซ์ไฟฟ้าที่ผ่านผิวปิดจะเห็นว่าสิ่งที่มีอยู่จริงในระบบคือประจุ q เพียงตัวเดียว แล้วเราต้องการหาอิทธิพลที่เกิดจากประจุที่ระยะห่างใดใด r เมื่อพิจารณาระบบจะเห็นว่าจุดใดใดที่ห่างจากประจุเป็นระยะทางที่เท่ากันจะไม่สามารถแยกแยะความแตกต่างได้เนื่องจากระบบมีสมมาตรในแนวรัศมี ดังนั้นในระบบนี้เราควรจินตนาการให้ผิวปิดสมมติเป็นรูปทรงกลมโดยให้มีรัศมีของผิวสมมติเป็น r แล้วคำนวณฟลักซ์ไฟฟ้าเพื่อหาค่าสนามไฟฟ้า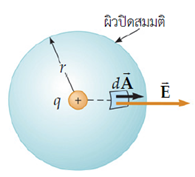พิจารณาผิวปิดทรงกลม จะเห็นว่าเวกเตอร์ปกติจะมีทิศตั้งฉากกับพื้นผิวทรงกลม ซึ่งทิศของเวกเตอร์ปกติจะมีทิศตั้งฉากกับทรงกลมและพุ่งออกจากผิวปิด และเมื่อพิจารณาทิศของสนามไฟฟ้าจะพบว่าทุกทุกจุดใดใดบนผิวปิดสนามไฟฟ้าก็มีทิศพุ่งออกและอยู่ในแนวเดียวกับเวกเตอร์ปกติเสมอ จะได้เมื่อพิจารณาผิวปิดทรงกลม ขนาดของสนามไฟฟ้าบนทุกทุกจุดบนผิวปิดทรงกลมมีขนาดเท่ากันดังนั้น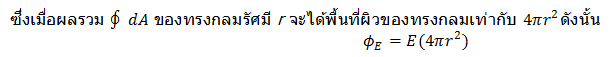จากกฎของเกาส์