แรง มวล และกฎการเคลื่อนที่
1. แรง (Force)
จากการศึกษาการเคลื่อนที่ของวัตถุในแนวตรง พบว่า วัตถุอาจมีการเคลื่อนที่ด้วยความเร็วคงตัว หรือมีการเปลี่ยนแปลงความเร็ว ซึ่งอะไรคือสาเหตุที่ทำให้วัตถุมีการเคลื่อนที่เป็นแบบดังกล่าว โดยปริมาณที่เกี่ยวข้องกับลักษณะการเคลื่อนที่ของวัตถุในแนวตรง ได้แก่ ระยะทาง, การกระจัด, อัตราเร็ว, ความเร็ว, ความเร่ง และช่วงเวลา หากเดิมมีวัตถุหยุดนิ่งอยู่กับที่แล้วต้องการให้วัตถุเคลื่อนที่ หรือถ้ากำลังเคลื่อนที่ด้วยความเร็วแล้วต้องการให้วัตถุเกิดการเปลี่ยนแปลงความเร็ว พบว่า จะต้องมีแรงมากระทำกับวัตถุ แสดงว่า แรงที่กระทำต่อวัตถุ จะทำให้วัตถุมีความเร็วเปลี่ยนไป ซึ่งอาจเปลี่ยนเฉพาะขนาด หรือทิศทาง หรืออาจเปลี่ยนทั้งขนาดและทิศทางก็เป็นได้
ภาพ แรง มวล และกฎการเคลื่อนที่
ที่มา ชาญ เถาวันนี
ดัดแปลงจาก https://www.haikudeck.com
ดังนั้น แรง คือ ความพยายามที่จะทำให้วัตถุเกิดการเปลี่ยนแปลง โดยการเปลี่ยนแปลงของวัตถุ มีในลักษณะต่างกัน เช่น รูปร่าง ตำแหน่ง หรือการหมุน ซึ่งเกิดจากการกระทำของแรงในลักษณะต่าง ๆ และอาจจะมีแรงมากกว่า 1 แรงที่มากระทำต่อวัตถุนั้น
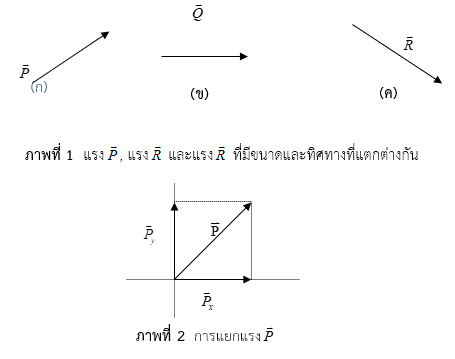
เนื่องจากแรงเป็นปริมาณที่มีทั้งขนาดและทิศทาง จึงจัดได้ว่าแรงเป็นปริมาณเวกเตอร์ มีหน่วยคือ นิวตัน (N) และ ![]()
1.1 องค์ประกอบของแรง

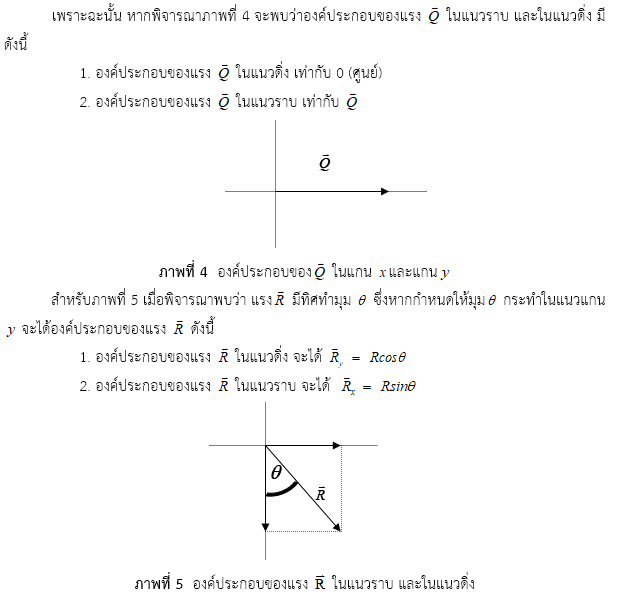
1.2 การหาแรงลัพธ์
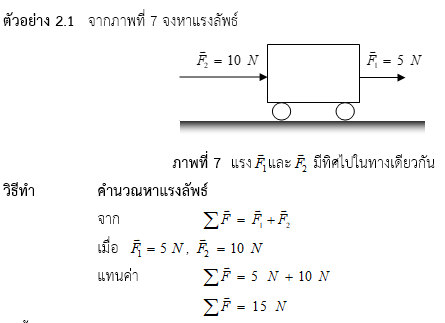
จากความรู้เบื้องต้นเกี่ยวกับเวกเตอร์ ถ้าหากมีแรงกระทำกับวัตถุมากกว่า 1 แรง จะสามารถรวมแรงเหล่านั้น หรือหาแรงลัพธ์ด้วยวิธีการทางเวกเตอร์ ซึ่งอาจจะสรุปวิธีการหาแรงลัพธ์ได้ ดังนี้
1. วิธีการวาดรูปแบบหางต่อหัว การหาแรงลัพธ์ด้วยวิธีการนี้ ต้องนำหางของแรงที่สองไปวางต่อหัวลูกศรของแรงแรก และนำหางของแรงที่สามไปตัวหัวของแรกที่ 2 ทำวิธีการนี้ไปเรื่อยๆ จนครบทุกแรง แรงลัพธ์ที่ได้ คือ แรงที่ลากจากหางของตัวแรกไปยังหัวของแรงตัวสุดท้าย
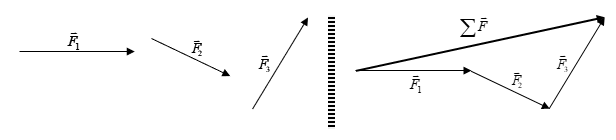
ภาพที่ 6 แสดงการหาแรงลัพธ์ โดยวิธีการวาดรูป
2. วิธีการคำนวณ ใช้สำหรับการหาแรงลัพธ์ของแรงย่อยที่มี 2 แรง แบ่งได้ 3 ลักษณะ คือ
2.1 แรงทั้งสองไปในทิศทางเดียวกัน แรงลัพธ์มีขนาดเท่ากับผลบวกของแรงทั้งสอง ส่วนทิศทางของแรงลัพธ์ ไปทางเดียวกับทิศทางของแรงทั้งสอง จะได้ว่า
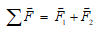
ดังนั้น แรงลัพธ์มีขนาด 15 นิวตัน มีทิศตามแกน



2. มวล และน้ำหนัก
2.1 มวล (Mass)
จากความรู้เรื่องแรง พบว่าแรงสามารถทำให้วัตถุเปลี่ยนสภาพการเคลื่อนที่ได้ แต่ในการเปลี่ยนสภาพการเคลื่อนที่ของวัตถุต่างๆ นอกจากจะขึ้นอยู่กับแรงแล้วยังพบว่ามีปริมาณอื่นที่มีความเกี่ยวข้องด้วย ดังตัวอย่างเหตุการณ์ต่อไปนี้ ถ้านำขวดพลาสติกขนาดเท่ากับ 3 ใบ แล้วใช้กระดาษหุ้มให้มิดชิด ใบแรกภายในวางเปล่า ใบที่สองเติมน้ำลงไปครึ่งขวด และใบที่สามเติมน้ำจนเต็มขวด แล้วแขวนไว้ในแนวดิ่งและลองขยับขวดไปมาในแนวระดับ ดังภาพที่ 12
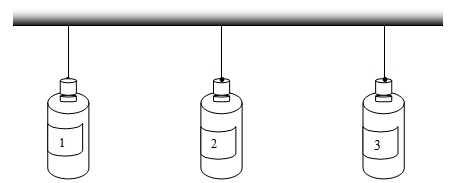
ภาพที่ 12 ขวด 3 ใบ ถูกแขวนในแนวดิ่ง
เมื่อขยับขวดขวดแต่ละใบในมือ โดยใช้แรงที่เท่ากัน การต้านมือของวัตถุเป็นความรู้สึกว่า เมื่อออกแรงผลักวัตถุ แล้ววัตถุไม่เคลื่อนที่หรือเมื่อให้ขวดทั้งสามใบแกว่งแล้วใช้มือต้านให้วัตถุหยุด ความยากง่ายหรือแรงที่ใช้ต้านทานการเคลื่อนที่ย่อมแตกต่างกัน โดยขวดที่บรรจุน้ำเต็มขวดจะรู้สึกว่าต้านทานการเปลี่ยนสภาพการเคลื่อนที่มากที่สุด และสำหรับขวดเปล่าจะรู้สึกว่าต้านทานการเปลี่ยนสภาพการเคลื่อนที่น้อยที่สุด จะเรียก สมบัติของวัตถุที่ต้านต่อการเปลี่ยนสภาพการเคลื่อนที่ของวัตถุนั้นว่า “ความเฉื่อย (Inertia)” และเรียกปริมาณที่บอกให้ทราบว่า วัตถุใดมีความเฉื่อยมากหรือน้อยว่า มวล
อาจสรุปได้ว่า มวล คือ ปริมาณที่บอกให้ทราบถึงการต้านการเปลี่ยนสภาพการเคลื่อนที่ของวัตถุ ซึ่งเป็นปริมาณสเกลาร์ ใช้สัญลักษณ์ คือ “ m ”มีหน่วยเป็น กิโลกรัม (kg )
2.2 น้ำหนัก (Weight)
จากการศึกษาการตกอย่างเสรีของวัตถุใกล้ผิวโลก พบว่า เมื่อมีแรงมากระทำกับวัตถุ จะทำให้วัตถุเคลื่อนที่ด้วยความเร่งคงตัว ซึ่งแรงที่มากระทำกับวัตถุนั้นคือ แรงดึงดูดของโลก ที่กระทำต่อวัตถุ อาจเรียกแรงนี้ว่า น้ำหนักของวัตถุ โดยที่ 
2.3.1 กฎการเคลื่อนที่ข้อที่หนึ่งของนิวตัน
จากการศึกษาเกี่ยวกับแรงและสภาพการเคลื่อนที่ พบว่า ถ้าวัตถุวางนิ่งอยู่บนพื้นราบแล้วไม่มีแรงอื่นใดมากระทำต่อวัตถุ วัตถุจะคงอยู่นิ่งต่อไปหรือถ้าให้แรง 2 สองแรงที่มีขนาดเท่ากันมากระทำกับวัตถุในทิศตรงข้ามกัน พบว่า วัตถุยังคงหยุดนิ่งเช่นเดิม
หรือถ้าพิจารณา วัตถุที่กำลังเคลื่อนที่บนพื้นระดับราบรื่น ซึ่งไม่มีแรงภายนอกใดมากระทำต่อวัตถุ วัตถุก็จะรักษาสภาพการเคลื่อนที่ด้วยความเร็วคงตัวค่าหนึ่ง หรือถ้าให้แรง 2 สองแรงที่มีขนาดเท่ากันมากระทำกับวัตถุในทิศตรงข้ามกัน พบว่า วัตถุยังคงรักษาสภาพการเคลื่อนที่ด้วยความเร็วคงตัวต่อไป
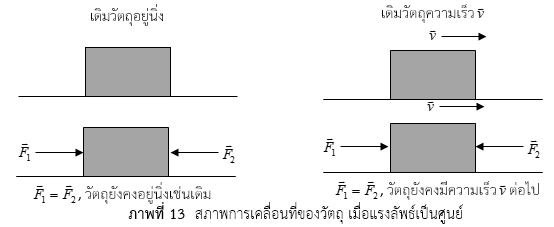
นิวตัน ได้สรุปเกี่ยวกับการรักษาสภาพการเคลื่อนที่ของวัตถุ มีใจความว่า “วัตถุจะรักษาสภาพอยู่นิ่งหรือสภาพการเคลื่อนที่อย่างสม่ำเสมอเป็นแนวตรง นอกจากจะมีแรงลัพธ์ที่ซึ่งมีค่าไม่เป็นศูนย์มากระทำ” สามารถกล่าวได้ว่า ผลรวมของแรงที่กระทำต่อวัตถุทั้งหมดมีค่าเป็นศูนย์
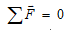
กฎการเคลื่อนที่ข้อที่หนึ่งของนิวตัน มีชื่อเรียกอีกชื่อหนึ่งว่า “กฎความเฉื่อย (Inertia Law)”
2.3.2 กฎการเคลื่อนที่ข้อที่สองของนิวตัน
จากการศึกษาสภาพการเคลื่อนที่ของวัตถุ และกฎการเคลื่อนที่ข้อที่หนึ่งของนิวตันทำให้ทราบว่าถ้าไม่มีแรงมากระทำหรือมีแรงหลายแรงมากระทำ แต่แรงลัพธ์ของแรงเหล่านั้นเป็นศูนย์แล้ววัตถุจะไม่มีการเปลี่ยนสภาพการเคลื่อนที่ แต่ถ้าแรงที่มีกระทำแล้วแรงลัพธ์ไม่เป็นศูนย์ วัตถุจะเปลี่ยนสภาพการเคลื่อนที่ คือ ความเร็วของวัตถุอาจเพิ่มขึ้นหรือลดลง หรืออาจเปลี่ยนทิศทางการเคลื่อนที่ ซึ่งเรียกว่า วัตถุมีความเร่ง ทั้งนี้ขึ้นอยู่กับขนาดและทิศทางของแรงลัพธ์ที่กระทำกับวัตถุ
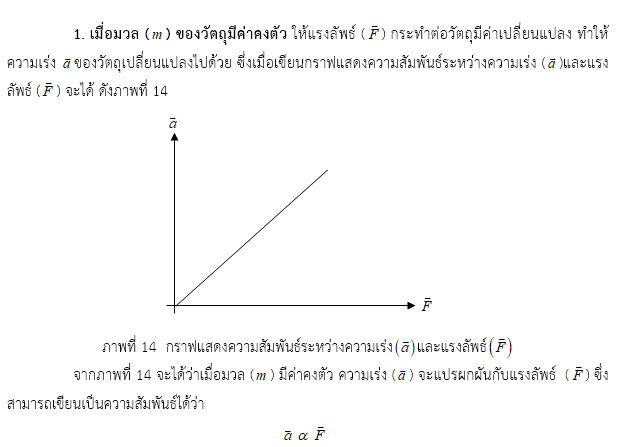
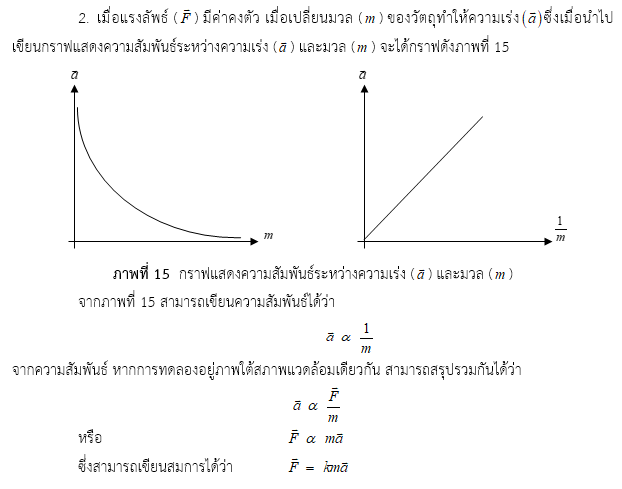
เมื่อ เป็นค่าคงที่ของการแปรผัน และจากนิยาม แรง 1 นิวตัน เป็นแรงที่ทำให้วัตถุมวล 1 กิโลกรัม เคลื่อนที่ด้วยความเร่ง 1 เมตรต่อวินาที2 จะทำให้ได้ k = 1 Ns2 / kgm
ดังนั้น จะได้

นิวตัน ได้สรุปเกี่ยวกับแรงและการเปลี่ยนสภาพการเคลื่อนที่ของวัตถุว่า “เมื่อมีแรงลัพธ์ที่มีค่าไม่เป็นศูนย์มากระทำต่อวัตถุ จะทำให้วัตถุเกิดความเร่งในทิศเดียวกับแรงลัพธ์ที่มากระทำ โดยขนาดของความเร่งนี้จะแปรผันตรงกับขนาดของแรงลัพธ์ แต่จะแปรผกผันกับมวลของวัตถุ” สรุปได้ว่า ผลรวมของแรงที่กระทำต่อวัตถุทั้งหมดมีค่าไม่เป็นศูนย์
2.3.3 กฎการเคลื่อนที่ข้อที่สามของนิวตัน
จากการศึกษากฎการเคลื่อนที่ข้อที่หนึ่งและสองของนิวตัน เป็นการอธิบายสภาพการเคลื่อนที่ของวัตถุ เมื่อมีแรงภายนอกมากระทำต่อวัตถุ ตากการศึกษาพบว่า เมื่อออกแรงกระทำต่อวัตถุ วัตถุ จะออกแรงตอบโต้ที่มากระทำนั้น เช่น เมื่อออกแรงดันกำแพง จะรู้สึกได้ว่ากำลังก็ออกแรงดันมือเช่นเดียวกัน และยิ่งออกแรงดันกำแพงมากขึ้นเท่าไร กำลังก็จะออกแรงดันมือมากขึ้นเท่านั้น
จากตัวอย่าง พบว่า เมื่อมีแรงกระทำต่อวัตถุหนึ่ง วัตถุนั้นจะออกแรงโต้ตอบในทิศตรงข้ามกับแรงที่มากระทำ แรงทั้งสองจะเกิดขึ้นพร้อมกันเสมอ เรียกแรงที่มากระทำต่อวัตถุว่า แรงกิริยา (action force) และเรียกแรงที่วัตถุโต้ตอบต่อแรงที่มากระทำว่า แรงปฏิกิริยา (reaction force) ซึ่งจะเรียกแรงทั้งสองว่า แรงคู่กิริยา-ปฏิกิริยา (action – reaction pairs) สามารถเขียนความสัมพันธ์ได้ว่า
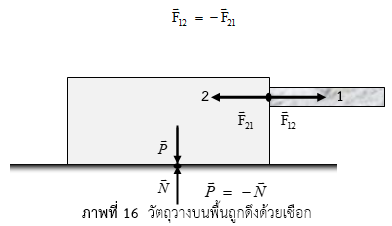
นิวตัน ได้สรุปความสัมพันธ์ระหว่างแรงกิริยากับแรงปฏิกิริยาว่า “ทุกแรงกิริยาย่อมมีแรงปฏิกิริยาขนาดเท่ากันกระทำในทิศตรงกันข้ามเสมอ หรือแรงกระทำซึ่งกันและกันของวัตถุสองก้อนย่อมมีขนาดเท่ากัน แต่มีทิศตรงกันข้าม” สรุปได้ว่า จะมีแรงเกิดขึ้นตรงตำแหน่งที่กระทำสองแรงขนาดเท่ากันแต่มีทิศตรงข้าม
2.4 กฎแรงดึงดูดระหว่างมวลของนิวตัน
ความคิดของมนุษย์ในสมัยโบราณ เชื่อว่า โลกเป็นศูนย์กลางของจักรวาล การเกิดกลางวันและกลางคืน การเห็นดวงอาทิตย์ ดวงจันทร์ ดาวตก ดาวหาง ตลอดจนเทหฟากฟ้าต่างๆ เหล่านี้ มนุษย์จะมีทั้งความยินดีและความกลัวคิดไปว่าคือ เทพเจ้าและการกระทำของเทพเจ้า
ต่อมาความคิดก็เปลี่ยนไปว่า โลกอาจไม่ใช่ศูนย์กลางของจักรวาล สิ่งต่างๆ ที่เกิดขึ้นนั้นไม่ใช่เทพเจ้าใดๆ โดยประมาณ ค.ศ.1500 นิโคลัส โคเปอร์นิคัส ชาวโปแลนด์พิสูจน์ได้ว่า โลกโคจรรอบดวงอาทิตย์
ทิโค บราห์ (Tycho Brahe, ค.ศ. 1546 - 1601) นักดาราศาสตร์ชาวเดนมาร์กสังเกตการเคลื่อนที่ของดาวเคราะห์และจดบันทึกตำแหน่งอย่างละเอียดทุกวันเป็นเวลานับสิบปี ผลการสังเกตครั้งนี้ทำให้เขา ไม่เชื่อในคำอธิบายการโคจรของดาวเคราะห์รอบดวงอาทิตย์ของโคเปอร์นิคัส (Nicolous Copernicus) ชาวโปแลนด์ ที่กล่าวว่าดาวเคราะห์เคลื่อนที่รอบดวงอาทิตย์เป็นวงกลม แต่ผลการสังเกตและการสรุปผลนี้ไม่เป็นผลสำเร็จในช่วงที่ทิโค บราห์ยังมีชีวิต อย่างไรก็ตามบราห์ได้มอบผลงานทั้งหมดนี้ให้แก่ผู้ช่วยของเขาชาวเยอรมมัน ชื่อ โยฮันเนส เคปเลอร์
โยฮันเนส เคปเลอร์ (Johannes Kepler, ค.ศ. 1571 - 1630) เคปเลอร์ได้บันทึกตำแหน่งดาวเคราะห์เพิ่มเติมแล้วจึงตั้งแบบจำลองที่อธิบายการเคลื่อนที่ของดวงดาวต่างๆ ว่าดาวเคราะห์จะโคจรรอบดวงอาทิตย์เป็นวงรี โดยมีดวงอาทิตย์อยู่ที่จุดโฟกัสของวงโคจรรูปวงรีนั้น ส่วนดาวฤกษ์ต่างๆ อยู่ในตำแหน่งประจำซึ่งไกลออกไปจากดาวเคราะห์ เคปเลอร์พบว่าการอธิบายข้อมูลจากการสังเกตของ ทิโค บราห์ด้วยแบบจำลองของเขาพบว่าแบบจำลองของเขาจะมีความถูกต้องแม่นยำมากกว่าการอธิบายด้วยแบบจำลองของโคเปอร์นิคัส โดยได้เสนอกฎ 3 ข้อ ดังนี้
1. กฎแห่งการโคจรเป็นวงรี กล่าวว่า “ทางโคจรของดาวเคราะห์เป็นรูปวงรี โดยมีดวงอาทิตย์อยู่ที่ตำแหน่งจุดโฟกัสจุดหนึ่ง”
2. กฎแห่งพื้นที่ กล่าวว่า “เมื่อดาวเคราะห์โคจรไปรอบดวงอาทิตย์ เส้นตรงที่ต่อระหว่างดวงอาทิตย์กับดาวเคราะห์นั้นจะกวาดพื้นที่ได้เท่ากันภายในเวลาเท่ากัน”
3. กฎแห่งคาบ กล่าวว่า “กำลังสองของคาบของดาวเคราะห์เป็นสัดส่วนโดยตรงกับกำลังสามของระยะทางเฉลี่ยดาวเคราะห์ไปยังดวงอาทิตย์” ดังนี้

จากผลการวิเคราะห์เกี่ยวการโคจรของดาวเคราะห์รอบดวงอาทิตย์ของเคปเลอร์ ทำให้นิวตัน เกิดความคิดว่า ทำไมดาวเคราะห์จึงโคจรรอบดวงอาทิตย์อยู่ได้ ทำไมจึงไม่หลุดออกไปจากวงโคจร แสดงว่าต้องมีแรงอย่างใดอย่างหนึ่งดึงเอาไว้ตลอดเวลา เลยคิดต่อไปว่า วัตถุบนโลกก็จะต้องถูกแรงนี้กระทำเหมือนกัน และมีทิศเข้าสู่ศูนย์กลางของจุดศูนย์กลางของระบบนั้น และแรงนี้จะมีทิศสู่ศูนย์กลางตลอดเวลา แรงนี้นิวตันคิดว่าน่าจะเกิดจากมวลของวัตถุ จึงเรียกแรงนี้ว่า แรงดึงดูดระหว่างมวล

2.4.1 มวลของโลก
วิธีการหนึ่งที่จะสามารถหามวลวัตถุได้ คือ การชั่ง แต่ทว่าวิธีการชั่วสามารถทำได้เฉพาะวัตถุที่มีขนาดเล็กเท่านั้น หากวัตถุมีขนาดใหญ่มากๆ เช่น โลก ดวงจันทร์ ดาวเคราะห์ต่าง จะไม่สามารถนำสิ่งเหล่านี้มาชั่งเพื่อหามวลได้ ดังนั้น การหามวลของวัตถุที่มีขนาดใหญ่มากๆ สามารถทำได้โดยการใช้กฎแรงดึงดูดระหว่างมวลของนิวตัน

2.4.2 ความเร่งโน้มถ่วง
สำหรับการหาความเร่งโน้มถ่วงสามารถแยกออกได้ 2 ลักษณะ ดังนี้
1. การหาความเร่งโน้มถ่วง ณ ตำแหน่งที่อยู่นอกดาวเคราะห์
ให้วัตถุมวล อยู่ห่างจากจุดศูนย์กลางของดาวเคราะห์ (x ) มวล mx เป็นระยะทาง R และมีความเร่งโน้มถ่วง g' ดังภาพที่ 18
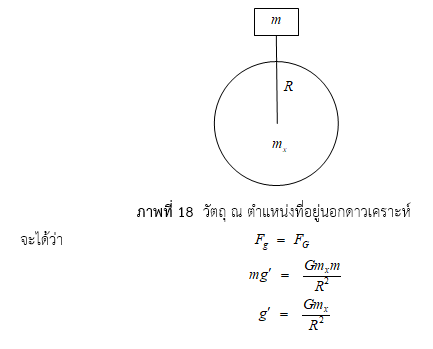
จากสมการ จะพบว่า ความเร่งโน้มถ่วงที่ตำแหน่งใดๆ จะแปรผกผันกับระยะทางจาก จุดศูนย์กลางโลกยกกำลังสอง ดังความสัมพันธ์
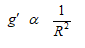
แสดงว่า ขนาดของความเร่งโน้มถ่วงจะลดลงเมื่อตำแหน่งนั้นอยู่ห่างจากดาวเคราะห์มากขึ้น
2. การหาความเร่งโน้มถ่วง ณ ตำแหน่งที่อยู่ในดาวเคราะห์

3. สภาพไร้น้ำหนัก
น้ำหนักบนดวงดาวต่าง คือ แรงโน้มถ่วงของดวงดาวที่กระทำต่อวัตถุ ซึ่งหาได้จากสมการ W = mg' และจากสมการการหาค่าความเร่งโน้มถ่วง ณ ตำแหน่งที่อยู่ห่างจากดาวเคราะห์ใด ๆ ที่ว่า
หมายความว่าน้ำหนักของวัตถุจะมีค่าน้อยตามไปด้วย ซึ่งก็ยังคงมีน้ำหนักอยู่บ้าง แต่จากการสังเกตของคนที่อยู่ในดาวเทียมที่กำลังโคจรรอบโลก จะรู้สึกว่าไม่มีน้ำหนักเลยที่เป็นเช่นนี้ เนื่องจากวัตถุทุกสิ่งที่อยู่ภายในดาวเทียม จะมีการเคลื่อนที่สัมพัทธ์กับดาวเทียมเป็นศูนย์ คือ อยู่นิ่งเมื่อเทียบกับดาวเทียม วัตถุที่อยู่ในดาวเทียมจึงลอยอยู่ในดาวเทียมได้โดยไม่ตก ซึ่งเรียกสภาพนี้ว่า สภาพไร้น้ำหนัก (weightlessness)



