เมื่อได้ยินคำว่า  "จำนวนเชิงซ้อน"  หลายคนอาจถึงกับเบือนหน้าหนี เพราะรู้สึกว่าจำนวนเชิงช้อนนั้น ชับซ้อน เป็นนามธรรม และเข้าใจได้ยาก ในบทความนี้ จะขอยกตัวอย่างปัญหาสนุก ๆ ที่อาจทำให้บางคนต้องเปลี่ยนความคิดและหันมาสนใจจำนวนเชิงซ้อน สำหรับคนที่รักคณิตศาสตร์โดยเฉพาะในเรื่องของจำนวนแล้ว ก็จะหลงเสน่ห์ของจำนวนเชิงซ้อนยิ่งขึ้นไปอีก

            ปัญหาดังกล่าวมีชื่อว่า "Treasure Island Problem" หรือ "เกาะมหาสมบัติ" เรื่องมีอยู่ว่า เด็กหนุ่มนักผจญภัยคนหนึ่งได้ค้นพบชิ้นส่วนที่มีลักษณะคล้ายหนังสัตว์ในกองเอกสารของปู่ทวดของเขา แผ่นหนังสัตว์นั้นได้ระบุลายแทงของที่ซ่อนขุมทรัพย์บนเกาะร้างแห่งหนึ่งโดยเขียนไว้ว่า

            “....เมื่อไปถึงเกาะร้างนั้น จะพบที่แขวนคอนักโทษซึ่งใช้แขวนคอกบฏในอดีต และมีตันโอ๊ก กับตันสนให้เริ่มต้นที่จุดที่พบที่แขวนคอนักโทษ แล้วเดินไปที่ตันโอ๊กพร้อมทั้งนับจำนวนก้าวที่เดิน เมื่อไปถึงต้นโอ๊กให้หันไปทางขวาเป็นมุมฉาก แล้วเดินต่อด้วยจำนวนก้าวเท่ากับที่เดินม าจาที่แขวนคอนักโทษ เมื่อถึงให้ทำเครื่องหมายตรงจุดนั้น จากนั้นให้กลับไปที่แขวนคอนักโทษอีกครั้ง แล้วให้เดินไปที่ต้นสน พร้อมทั้งนับจำนวนก้าวที่เดิน เมื่อไปถึงต้นสนให้หันไปทางซ้ายเป็นมุมฉาก แล้วเดินต่อด้วยจำนวนก้าวเท่ากับที่เดินมาจากที่แขวนคอนักโทษ เมื่อถึงให้ทำเครื่องหมายอีกตรงจุดนั้น จุดที่ฝังขุมทรัพย์อยู่บริเวณกึ่งกลางระหว่างจุดที่ทำเครื่องหมายทั้งสอง"

            จะเห็นว่า ลายแทงได้กล่าวไว้อย่างชัดเจนว่าจะหาขุมทรัพย์ได้อย่างไร แต่ทว่า เมื่อเด็กหนุ่มไปถึงเกาะร้างเขากลับพบเพียงต้นโอ๊กและต้นสน ไม่ว่าเขาจะพยายามหาเท่าไร ก็ไม่พบที่แขวนคอนักโทษบนเกาะนั้น สาเหตุที่เป็นเช่นนี้ก็เพราะลายแทงนี้ได้ถูกเขียนขึ้นนานมากแล้ว ลม แสงแดด และฝนต่างได้ชะล้างบริเวณที่เคยแสดงที่แขวนคอนักโทษจนไม่เหลือร่องรอย เด็กหนุ่มรู้สึกหมดหวัง และโกรธ จึงเริ่มขุดไปทั่วทั้งเกาะ แต่ความพยายามของเขาไร้ประโยชน์ เนื่องจากเกาะมีขนาดใหญ่มากเขาจึงต้องกลับบ้านมือเปล่าในที่สุด แต่ถ้าเด็กหนุ่มมีความรู้เรื่องคณิตศาสตร์ โดยเฉพาะเรื่องจำนวนเชิงซ้อน เขาคงค้นพบขุมทรัพย์ไปแล้ว

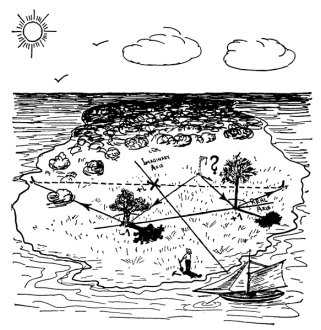
รูปที่ 1 ล่าขุมทรัพย์กับจำนวนเชิงซ้อน (Gamow: 1947)

            การนำจำนวนเชิงซ้อนไปใช้ไขปัญหาขุมทรัพย์นี้ จะต้องทำความเข้าใจความหมายของการคูณจำนวนเชิงซ้อนก่อน จากที่เคยเรียนมาแล้วว่า การคูณจำนวนเชิงซ้อนด้วยจำนวนจริงเปรียบได้กับการคูณเวกเตอร์ด้วยปริมาณสเกลาร์ ตัวอย่างเช่น เมื่อนำจำนวนจริง 3 ไปคูณจำนวนเชิงซ้อน 2+3i จะได้ 6+9i หรือกล่าวว่า

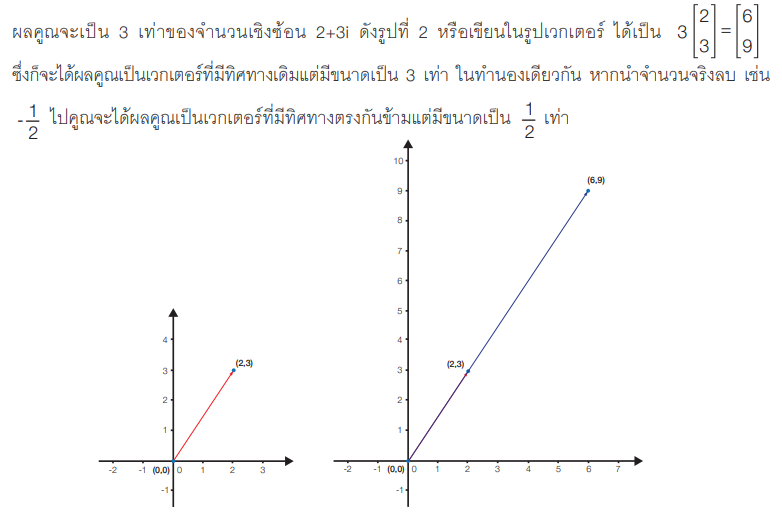
รูปที่ 2 การคูณ 2+3i ด้วย 3

            ลองพิจารณาการคูณจำนวนเชิงซ้อนด้วย i เมื่อคูณ 1 ด้วย จะได้ i และเมื่อคูณผลคูณด้วย i ไปเรื่อย ๆ จะได้ -1, -i และ 1 ตามลำด้บ สามารถเขียนแสดงในรูปเวกเตอร์ได้ดังรูปที่ 3

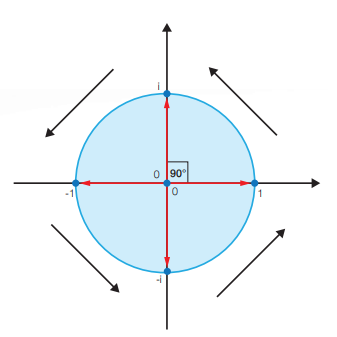
รูปที่ 3 การคูณ 1 ด้วย i

            การคูณจำนวนเชิงซ้อนด้วย  เป็นการหมุนเวกเตอร์รอบจุด (0,0) เป็นมุม 90 องศา ในทิศทวนเข็มนาฬิกาในทำนองเดียวกัน การคูณจำนวนเชิงซ้อนด้วย -i เป็นการหมุนเวกเตอร์รอบจุด (0,0) ไปเป็นมุม 90 องศาในทิศตามเข็มนาฬิกา

            เมื่อนำลายแทงขุมทรัพย์มาเขียนลงบนระนาบเชิงซ้อน ดังรูปที่ 4 โดยกำหนดจุด R(a.b) แทนตำแหน่งของที่แขวนคอนักโทษ จุด P และ Q แทน ตำแหน่งต้นสนและต้นโอ๊ก ตามลำดับ ให้แกนจริงเป็นเส้นตรงที่ผ่านต้นไม้ทั้งสองต้น และแกนจินตภาพเป็นเส้นตรงที่ตั้งฉากกับแกนจริงและตัดแกนจริงที่จุดกึ่งกลางระหว่างต้นไม้ทั้งสองโดยไม่เสียนัยทั่วไป เราสามารถกำหนดให้ P มีพิกัดเป็น (1,0) และ Q มีพิกัดเป็น (-1,0)

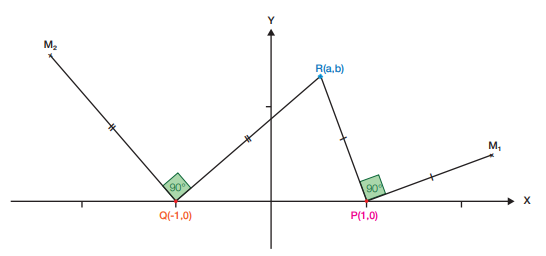
รูปที่ 4 ลายแทงขุมทรัพย์บนระนาบเชิงซ้อน

            จะสังเกตเห็นว่า เวกเตอร์ RP ที่เกิดจากการเดินจากที่แขวนคอนักโทษไปยังต้นสน สามารถมองได้เป็นจำนวนเชิงซ้อน (1-a)-bi การหันไปทางซ้ายเป็นมุมฉากเปรียบได้กับการคูณ (1-a)-bi ด้วย i ซึ่งได้เป็น 6+(1-a)I ดังนั้น จากรูปที่ 5 จะได้ว่า พิกัดของจุด M₁ คือ (1+b, 1-a)

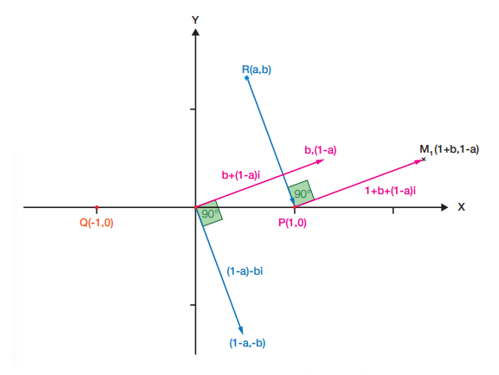
รูปที่ 5 การคำนวณหาพิกัดของจุด M₁

             ในทำนองเดียวกัน จะได้พิกัดของจุด M2 คือ (-1-b,1+a) ดังแสดงในรูปที่ 6

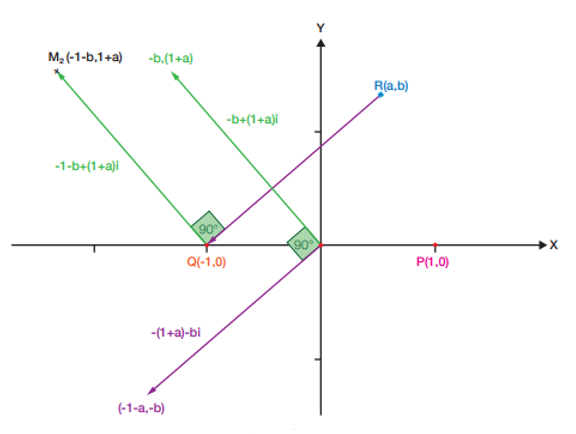
รูปที่ 6 การคำนวณหาพิกัดของจุด M₂

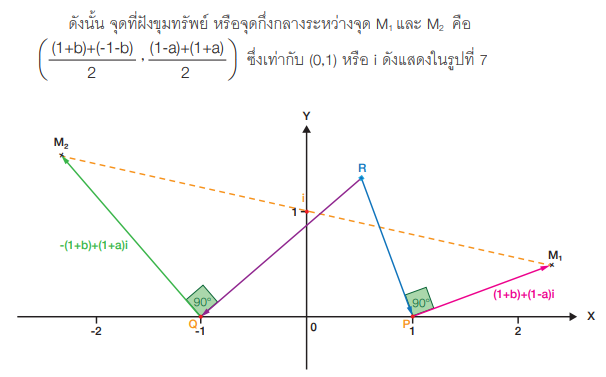
รูปที่ 7 การคำนวณหาพิกัดของจุดที่ฝังขุมทรัพย์

            จากรูป จะเห็นว่าจุดที่ฝังขุมทรัพย์มีพิกัดเป็น (0,1) ซึ่งก็คือ จุดที่ห่างจากจุดกึ่งกลางของตันไม้ทั้งสองต้นไปทางเหนือ โดยจุดที่ฝังขุมทรัพย์มีระยะห่างจากจุดกึ่งกลางเท่ากับระยะทางจากจุดกึ่งกลางไปยังตันไม้ต้นใดต้นหนึ่งจะสังเกตเห็นว่า พิกัดที่ได้ไม่ขึ้นกับ a และ b เลย นั่นแ เสดงว่า ตำแหน่งของจุดที่ฝังขุมทรัพย์ สามารถหาได้จากตำแหน่งของต้นโอ๊กและตันสน โดยไม่จำเป็นต้องรู้ตำแหน่งที่แขวนคอนักโทษ

            การคูณจำนวนเชิงซ้อนด้วย i และ -i ดังที่กล่าวข้างต้น เปรียบได้กับการหมุนเวกเตอร์บนระนาบสองมิติทำให้สามารถแก้ปัญหาข้างต้นได้ง่ายขึ้น ผู้ที่สนใจวิธีคิดอย่างละเอียดสามารถศึกษาเพิ่มเติมได้จากสื่อวีดิทัศน์ชุด "Math in My Life เพราะคณิตอยู่ในชีวิตจริง "Season 2 ซึ่งจัดทำโดย สาขาวิชาคณิตศาสตร์ สสวท. ติดตามได้ทาง YouTube ช่อง IPST Thailand

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Azad, Kalid. A Visual, Intuitive Guide to Imaginary Numbers. สืบคั้นเมื่อ 30 พฤษภาคม 2558, จาก http://betterexplained.com/articles/a-visual-intuitive-guide-to-imaginary-numbers/

Gamow, George. (1947). One, Two, Three ... Infinity: Acts and Speculations of Science.  NY: Dover Publications.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2553). หนังสือเรียนรายวิชาเพิ่มเติม คณิตศาสตร์ เล่ม 3 ชั้นมัธยมศึกษาปีที่ 4-6 กลุ่มสาระการเรียนรู้ณิตศาสตร์ ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551.กรุงเทพมหานคร: โรงพิมพ์องค์การค้า สกสค.

สถาบันส่งเสริ่มการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2553). หนังสือเรียนรายวิชาเพิ่มเติม คณิตศาสตร์ เล่ม 4 ชั้นมัธยมศึกษาปีที่ 4-6 กลุ่มสาระการเรียนรู้ณิดศาสตร์ ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551.กรุงเทพมหานคร: โรงพิมพ์องค์การค้า สกสค.