รูปที่ 1 หนังสือพิมพ์ The Wall Street Journal
ที่มา:   http://www.wsj.com/articles/the-best-language-for-math-1410304008

            หนังสือพิมพ์ The Wall Street Journal ฉบับวันที่ 15 กันยายน ค.ศ. 2014 ได้ตีพิมพ์บทความซื่อ The Best Language for Math ซึ่งเรียบเรียงโดย Sue Shellenbarger เนื้อหาในบทความนี้กล่าวถึงผลการวิจัยด้านคณิตศาสตร์ศึกษาที่ระบุว่า ในบรรดาภาษาที่ใช้สื่อสารกันในโลก ภาษาจีนภาษาญี่ปุ่นและภาษาเกาหลี เป็นภาษาที่เอื้อต่อการเรียนรู้คณิตศาสตร์ของนักเรียนระดับประถมศึกษามากที่สุด เมื่อเปรียบเทียบวิธีการใช้คำบอกจำนวน(ต่อไปจะเรียกว่า ชื่อจำนวน) ในภาษาจีนเทียบกับภาษาอื่น ๆ โดยเฉพาะภาษาอังกฤษแล้ว ชื่อจำนวนในภาษาจีนมีแบบแผนที่สอดคล้องกับการเขียนตัวเลขแสดงจำนวนในระบบฐานสิบ และการเขียนตัวเลขด้วยอักขระฮินดูอารบิกซึ่งใช้กันทั้งในชีวิตประจำวันและในการศึกษาวิชาคณิตศาสตร์อย่างตรงไปตรงมามากที่สุด ซึ่งทำให้ผู้เรียนที่ใช้ภาษาจีนเป็นภาษาหลักในการเรียนคณิตศาสตร์สามารถเข้าใจหลักการของค่าประจำหลักสิบ และหลักหน่วยของจำนวนโดยเฉพาะตั้งแต่ 1 ถึง 99 ได้ดีกว่าในภาษาอื่น

รูปที่ 2 Sue Shellenbarger
ที่มา:  http://alumni.msu.edu/newsarticle.cfm?id=470

การนับในกาษาจีน

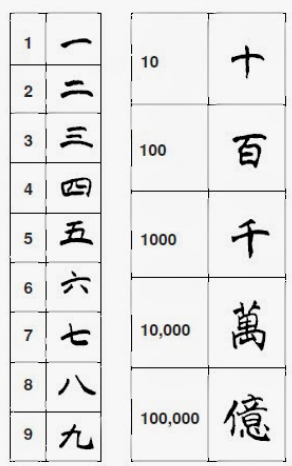
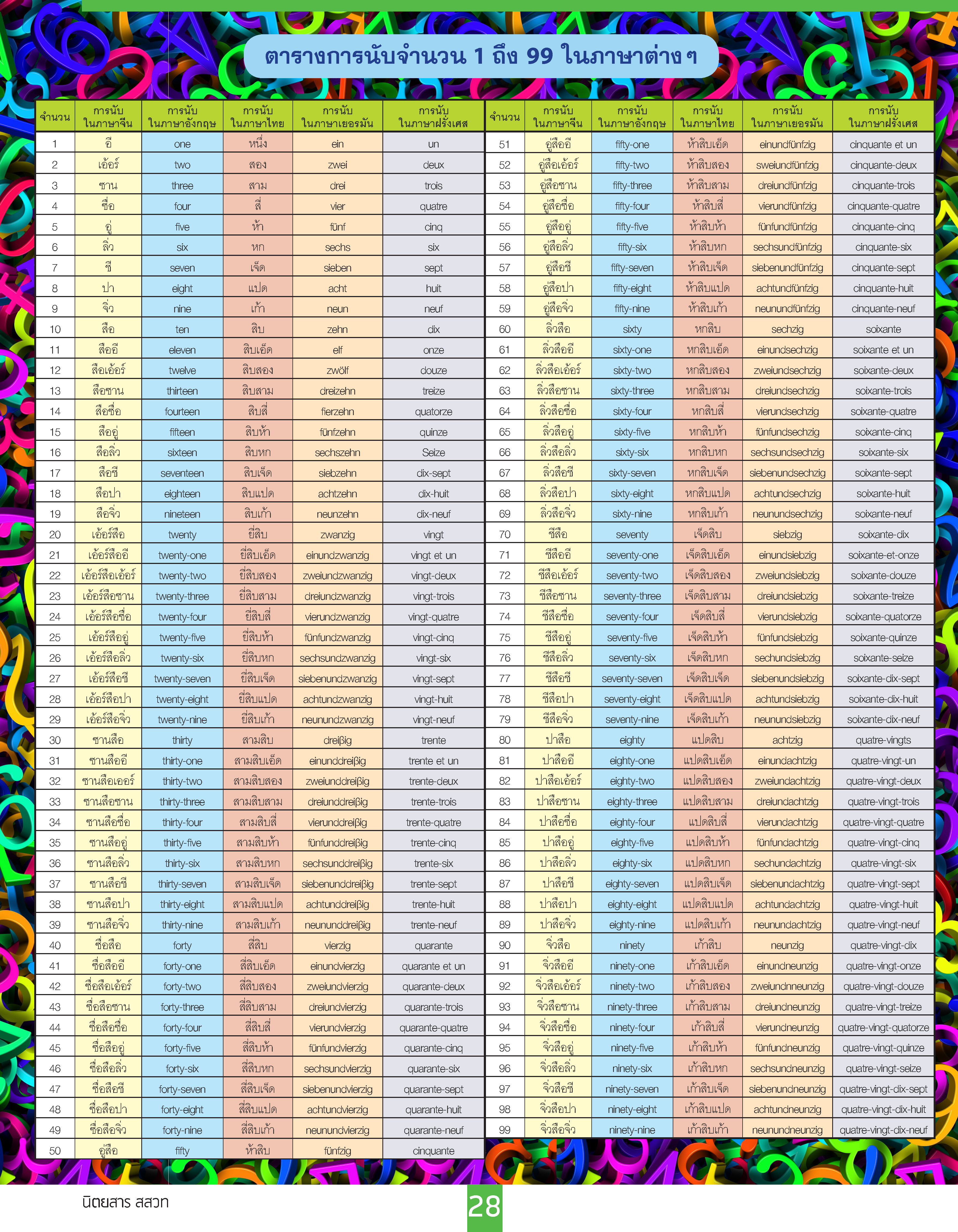
            จากตารางการนับจำนวน 1 ถึง 99 ในภาษาต่าง ๆ ที่อยู่ท้ายบทความนี้ มีข้อน่าสังเกตว่าภาษาจีนมีชื่อเรียกจำนวนตั้งแต่ 1 ถึง 10 ที่แตกต่างกัน นั่นคือ อี เอ้อ ซาน ซื่อ อู่ ลิ่ว ชี ปา จิ่วสือ ตามลำดับ การเรียกจำนวน 11 ถึง 19 ก็เริ่มตันด้วยการขานชื่อสิบนั่นคือ ลือ แล้วตามด้วยชื่อตัวเลขในหลักหน่วยที่ต้องการ เช่น 16 ก็จะขานว่า สือ-ลิ่ว ซึ่งก็คือ  สิบ-หก คล้ายภาษาไทย สำหรับจำนวนตั้งแต่ 20 ถึง 99 ก็จะเริ่มตันด้วยการขานชื่อตัวเลขประจำหลักสิบก่อน ตามด้วยการขานชื่อสิบ แล้วตามด้วยชื่อตัวเลขในหลักหน่วย เช่น 72 จะขานว่า ชี-สื่อ-เอ้อ หรือ เจ็ด-สิบ-สอง ดังนั้นความหมายเชิงเลขคณิตของการเรียกชื่อตัวเลขใน 72 ว่า ชี-ลือ-เอ้อ ในภาษาจีน จึงสามารถแสดงให้อยู่ในรูปการดำเนินการทางคณิตศาสตร์ได้ว่า มันคือ ของ 7 กอง กองละ 10 ชิ้น รวมกับอีก 2 ชิ้น หรือ (7x10) + 2 = 72 นั่นเอง

            เมื่อสังเกตการเรียกชื่อจำนวนในภาษาจีนจากตารางแล้ว จะเห็นได้ว่า ภาษาจีนรักษาแบบแผนการเรียกชื่อจำนวนในลักษณะนี้อย่างเคร่งครัดโดยไม่มีข้อยกเว้นซึ่งก็เป็นวิธีการนับคล้ายกับในภาษาญี่ปุ่น และภาษาเกาหลีที่แม้จะเรียกชื่อจำนวน 1 ถึง 10 ไม่เหมือนกัน แต่ก็ใช้แบบแผนในการเรียกชื่อจำนวน 1 ถึง 99ในลักษณะเดียวกับในภาษาจีนทุกประการ

รูปที่ 3 การนับภาษาจีน

ที่มา: http://ratiihayu.blogspot.com/2014/01/the-earlier-number-system-and.html

การนับในกาษาอังกฤษ

            การเรียกชื่อจำนวนในภาษาอังกฤษไม่ได้กำหนดชื่อเฉพาะให้กับจำนวน 1 ถึง 10 เท่านั้น แต่ยังมีชื่อเรียกเฉพาะให้จำนวน 11 และ 12 นั่นคือ eleven และ twelve และเรียกจำนวน 13 ถึง 19 ด้วยคำว่า -teen เช่น thirteen, fourteen, fifteen. แล้วเรียกชื่อจำนวนพหุคูณของสิบด้วยคำว่า -ty เช่น twenty, thirty, forty การที่ภาษาอังกฤษมีชื่อเฉพาะสำหรับจำนวน 11 และ 12 และการใช้คำว่า -teen กับ -ty นี้อาจทำให้การเรียกชื่อจำนวนในภาษาอังกฤษมีแบบแผนที่แตกต่างจากระบบการเขียนตัวเลขแสดงจำนวนในระบบฐานสิบ เนื่องจากจำนวน เช่น 12 ซึ่งใช้คำว่า twelve หรือ 17 ซึ่งใช้คำว่า seventeen ไม่ปรากฏความสัมพันธ์ที่เชื่อมโยงกับค่าประจำหลักสิบในลักษณะเดียวกับในภาษาจีน ความซับซ้อนในการเรียกชื่อจำนวน 1 ถึง 20 ในภาษาอังกฤษจึงอาจเป็นเหตุผลที่ทำให้นักเรียนที่ใช้ภาษาอังกฤษเป็นภาษาหลักไม่มีโอกาสสัมผัสกับโครงสร้างของค่าประจำหลักสิบและหลักหน่วยในการขานซื่อจำนวนโดยเฉพาะเมื่อเขาเริ่มต้นรู้จักวิธีการนับจำนวน 1 ถึง 20 แล้วต้องมาทำความเข้าใจเรื่องค่าประจำหลักใหม่หลังจากที่ได้เริ่มต้นเรียนคณิตศาสตร์แล้ว บทความของ Sue Schellenbarger ได้อ้างถึงงานวิจัยของ Ho & Fuson (1998) ที่ได้ศึกษาเปรียบเทียบความเข้าใจเรื่องค่าประจำหลักของจำนวนตั้งแต่ 11 ถึง 19 ระหว่างเด็กจีนและเด็กที่ใช้ภาษาอังกฤษทั้งในสหราชอาณาจักรและสหรัฐอเมริกา และพบว่าในวัย 5 ขวบ เด็กจีนจะเริ่มเข้าใจและเห็นความสัมพันธ์ระหว่างหลักสิบและหลักหน่วย ในขณะที่เด็กที่ใช้ภาษาอังกฤษไม่ปรากฎความเข้าใจลักษณะนี้ในช่วงวัยเดียวกัน ซึ่งวิธีการเรียกชื่อจำนวน 1 ถึง 20 ที่ไม่เหมือนกันในภาษาจีนและภาษาอังกฤษน่าจะเป็นสาเหตุที่ทำให้เกิดความแตกต่างในผลการวิจัยนี้

รูปที่ 4 การนับภาษาอังกฤษ

ที่มา: http://4.bp.blogspot.com/-YJqlaHv-A4w/VpYkR4KKZ1I/AAAAAAAAAAg/wBC9d0TxDe0/s1600/unnamed.png

การนับในกาษาไทย

            เมื่อพิจารณาการเรียกชื่อจำนวน 1 ถึง 99 ในภาษาไทยของเราดังแสดงไว้ในตาราง จะพบว่ามีการเรียกชื่อที่ใกล้เคียงกับภาษาจีนมาก นั่นคือในการขานจำนวนสองหลัก เช่น 72 จะเริ่มต้นด้วยการขานชื่อตัวเลขหลักสิบก่อน ตามด้วยการขานชื่อหลักสิบแล้วตามด้วยชื่อตัวเลขหลักหน่วย ซึ่งก็จะได้ว่า 'เจ็ด-สิบ-สอง' ตามวิธีการเดียวกับการเรียกชื่อจำนวนในภาษาจีนว่า 'ชี-สือ-เอ้อ' โดยสามารถแสดงการดำเนินการทางเลขคณิตที่ละไว้ได้ว่า เจ็ด(คูณสิบ(แล้วบวก)สอง หรือ (7x10) +2 = 72 เพียงแต่จะมีข้อยกเว้นอยู่สองจุด คือ หาก 1 เป็นตัวเลขประจำหลักหน่วยของตัวเลขสองหลักเมื่อใด เราจะเปลี่ยนจากการขาน "หนึ่ง' เป็น 'เอ็ด' เช่น สี่-สิบ-เอ็ด" และหาก 2 เป็นตัวเลขประจำหลักสิบเมื่อใด เราจะเปลี่ยนจากการขาน 'สอง' เป็น 'ยี่' เช่น ยี่-สิบ-สอง' ซึ่งก็เป็นวิธีการเรียกชื่อจำนวนที่ใช้กันมาตั้งแต่สมัยโบราณการใช้คำว่า 'เอ็ด' และ 'ยี่' นี้เองที่อาจทำให้การเรียกชื่อจำนวน 1 ถึง 100 ในภาษาไทยมีแบบแผนการนับที่ซับซ้อนกว่าในภาษาจีน และอาจทำให้นักเรียนไม่เห็นความเชื่อมโยงของการที่ 1 เป็นเลขประจำหลักหน่วยของตัวเลขสองหลัก เนื่องจากได้เปลี่ยนไปเรียกว่า 'เอ็ด" และความเชื่อมโยงของการที่ 2 เป็นตัวเลขประจำหลักสิบ เนื่องจากได้เปลี่ยนไปเรียกว่า 'ยี่' เสียแล้วประเด็นที่เกี่ยวกับการนับนี้แม้จะเป็นเรื่องที่เราคุ้นเคยกันมานานแล้ว แต่ในการเริ่มต้นสอนคณิตศาสตร์ในเรื่องค่าประจำหลัก ครูผู้สอนจำเป็นต้องเชื่อมโยงคำว่า "เอ็ด" กับ "หนึ่ง" และ "ยี่" กับ "สอง" ตามลำดับเพื่อให้เห็นกลไกการคำนวณที่แฝงอยู่ในการนับ เช่นจำนวน 'ยี่-สิบ-เอ็ด' ซึ่งนักเรียนควรสามารถเชื่อมโยงได้ว่ามันคือ สอง(คูณสิบ(แล้วบวก)หนึ่ง หรือ (2x10) + 1 = 21  แม้ว่าในคำว่า ยี่-สิบ-เอ็ด' จะไม่มีคำว่า สองหรือ หนึ่ง ปรากฏอยู่เลย ดังนั้นจึงเป็นข้อสังเกตได้ว่า หากการนับในภาษาไทยจะเปลี่ยนจากการขานคำว่า 'เอ็ด' กับ ยี่' มาเป็น "หนึ่ง' กับ 'สอง' เสีย ภาษาไทยก็จะกลายเป็นภาษาที่สอดคล้องกับระบบการนับด้วยตัวเลขฐานสิบที่ใช้ในคณิตศาสตร์เหมือนภาษาจีน ภาษาญี่ปุ่น หรือภาษาเกาหลีแต่เนื่องจากการนับในลักษณะนี้เราได้ใช้กันจนเคยชินแล้วจึงอาจเป็นเรื่องยากที่จะเปลี่ยนแปลง

การนับในกาษาเยอรมันและกาษาฝรั่งเศส

            หลังจากที่บทความดังกล่าวได้ตีพิมพ์เผยแพร่ไปได้มีเสียงสะท้อนแสดงความสงสัยและการไม่เห็นด้วยจากผู้อ่านจำนวนมาก โดยส่วนใหญ่จะยังคลางแคลงใจว่าผลสัมฤทธิ์ทางคณิตศาสตร์ของการสอบระดับนานาชาติในกลุ่มนักเรียนจีนที่มักจะสูงกว่าชาติอื่น ๆ เป็นผลจากโครงสร้างด้านภาษาและการนับเหล่านี้จริงหรือไม่ เพราะหากจะมองจากเนื้อหาของข้อสอบเหล่านี้จริง ๆ ส่วนใหญ่จะประเมินทักษะทางคณิตศาสตร์ที่มีความซับซ้อนมากกว่าการนับเบื้องต้นเหล่านี้ นอกจากนี้ยังมีการตั้งข้อสังเกตอีกด้วยว่าการนับในภาษาอื่น ๆ ที่มีกลไกการคำนวณทางคณิตศาสตร์ที่ซับซ้อนมากกว่าซ่อนอยู่ อาจเป็นการกระตุ้นให้นักเรียนรู้จักการดำเนินการทางคณิตศาสตร์ตั้งแต่รู้จักการนับเสียด้วยซ้ำตัวอย่างเช่น การเรียกชื่อจำนวน 20 ถึง 99 ในภาษาเยอรมันตามที่แสดงไว้ในตาราง จะใช้วิธีการขานตัวเลขหลักหน่วยก่อนจากนั้นจะตามด้วยคำว่า und (อุนด์) ซึ่งแปลว่า "กับ" ก่อนจะขานตัวเลขพหุคูณของสิบซึ่งมีชื่อเรียกเฉพาะ เช่น ในการขานจำนวน 53 จะขานเลขสามก่อนนั่นคือ drei (ไดร) ตามด้วยคำว่า und แล้วปิดท้ายด้วยการขานคำว่าห้าสิบ นั่นคือ funfzig (ฟื้นฟ์ซิก) รวมเป็น dreiundfunfzig (ไดรอุนด์ฟินฟ์ซิก) ซึ่งไม่เพียงแต่จะแสดงให้เห็นถึงความเป็นไปได้ในการรวมค่าประจำหลักหน่วยและหลักสิบที่สามารถเริ่มตันจากหลักหน่วยก่อนได้ แต่ยังมีการใช้คำว่า und หรือ กับ อย่างชัดเจนซึ่งสามารถแทนได้ด้วยการดำเนินการ "บวก" ในคณิตศาสตร์กลไกการคำนวณทางเลขคณิตที่ซ่อนอยู่ในการขานจำนวน 53 ในภาษาเยอรมันจึงสามารถเขียนได้เป็น 3+50 - 53 ซึ่งแตกต่างไปจากโครงสร้างในภาษาอื่น ๆ อย่างชัดเจน

รูปที่ 5 การนับภาษาเยอรมันและภาษาฝรั่งเศส
ที่มา: http://pad2.whstatic.com/images/thumb/5/56/Write-German-Numbers-Step-1.jpg/728px-Write-German-Numbers-Step-1.jpg

            นอกจากนี้ การเรียกชื่อจำนวน 70 ถึง 99 ในภาษาฝรั่งเศส ได้มีการใช้การดำเนินการทางคณิตศาสตร์ที่ซับซ้อนมากยิ่งขึ้น โดยจำนวนตั้งแต่ 70 ถึง 79 จะใช้วิธีการบวกจำนวน 60 ด้วย จำนวน 10 ถึง 19 ตามลำดับ เช่น จำนวน 72 จะขานว่า soixante-douze (ซิ้วซองเตอ-ดูซ) ซึ่งแปลตรงตัวได้ว่า หกสิบ-สิบสอง และสามารถเขียนเป็นการดำเนินการทางคณิตศาสตร์ได้ 60+12 - 72 หรือจำนวน 79 จะขานว่า soixante-dix-neuf (ซิ้วซองเตอ-ดิซ-เนิฟ) ซึ่งแปลตรงตัวได้ว่า หกสิบ-สิบ-เก้า และสามารถเขียนเป็นการดำเนินการทางคณิตศาสตร์ได้ว่า 60+10+9 ซึ่งซับซ้อนกว่าการบวกของหลักสิบและหลักหน่วยตามที่ใช้กันทั่วไปในภาษาอื่น ๆ แต่กลุ่มตัวเลขที่มีใครงสร้างในการขานซับซ้อนมากที่สุดในภาษาฝรั่งเศส คือจำนวน 80 ถึง 99 โดยจำนวน 80 จะเรียกกันว่า quatre-vingts (ทัทตรอะ-แวงต์ส์) ซึ่งแปลตรงตัวได้ว่า สี่-ยี่สิบ เพื่อแสดงว่าจำนวนแปดสิบคือจำนวนยี่สิบสี่ชุดและในการขานจำนวน 81 ถึง 99 ก็ให้เพิ่มจำนวน 1 ถึง 19 ต่อท้ายไป ทำให้การขานจำนวน 81 ถึง 99 ในภาษาฝรั่งเศสมีความซับซ้อนและยาวกว่าในภาษาอื่น ๆ เช่น จำนวน 98 จะขานว่า quatre-vingt-dix-huit (กัทเตรอะ-แวงศ์ส์-ดีส-วีท) ซึ่งแปลตรงตัวได้ว่า สี่-ยี่สิบ-สิบ-แปด และสามารถเขียนเป็นการดำเนินการทางคณิตศาสตร์ได้เป็น (4x20+(10+8) = 98 จึงเห็นได้ว่ามีการใช้การดำเนินการทั้งการคูณและการบวกที่ขับข้อนและแตกต่างจากลักษณะการดำเนินการในจำนวนสองหลักในภาษาจีนและภาษาไทยเป็นอย่างมาก

            ซึ่งความซับซ้อนของการขานจำนวนสองหลักในภาษาเยอรมันและภาษาฝรั่งเศสเหล่านี้ สามารถยกเป็นประเด็นอภิปรายได้ว่า ในการขานจำนวนด้วยภาษาเหล่านี้ซึ่งเป็นทักษะที่นักเรียนได้เรียนรู้ก่อนจะรู้จักการดำเนินการทางคณิตศาสตร์ อาจทำให้พวกเขามีมโนทัศน์เกี่ยวกับการบวกการคูณ และสมบัติการสลับที่ ตั้งแต่เริ่มรู้จักการนับก็ได้ ซึ่งอาจส่งผลให้นักเรียนเข้าใจกลไกการคำนวณทางคณิตศาสตร์เหล่านี้ได้ดียิ่งขึ้นในเวลาต่อมา

รูปที่ 6 การเรียนการสอนในแต่ละประเทศ
ที่มา: http://www.wsj.com/news/interactive/WORKFAM0910

สรุป

            จากตัวอย่างที่ได้แสดงในบทความนี้จะเห็นได้ว่าภาษาและการนับมีความละเอียดอ่อนต่อการศึกษาหลักการทางคณิตศาสตร์ของนักเรียนอย่างมีนัยสำคัญ และความแดกต่างของโครงสร้างการขานจำนวนในแต่ละภาษาอาจส่งผลต่อความเข้าใจเรื่องค่าประจำหลักและระบบการเขียนตัวเลขฐานสิบของนักเรียนที่แตกต่างกันได้ แต่น่าเสียดายที่ยังไม่มีงานวิจัยที่เน้นศึกษาปัจจัยด้านความแตกต่างทางการขานจำนวนในแต่ละภาษากับการเรียนรู้คณิตศาสตร์ของนักเรียนอย่างจริงจัง เหตุผลหนึ่งอาจเป็นเพราะนอกจากผู้วิจัยจะต้องมีความเข้าใจด้านคณิตศาสตร์ศึกษาเป็นพื้นฐานแล้วอาจจำเป็นต้องมีความเชี่ยวชาญในภาษาต่าง ๆ มาประกอบกันไปด้วย แม้แต่ในภาษาไทยเอง ปฏิกิริยาของนักเรียนที่มีต่อคำว่า "เอ็ด" กับ "ยี่" กับการเรียนรู้คณิตศาสตร์เกี่ยวกับค่าประจำหลักของตัวเลข 1 และ 2 ก็เป็นหัวข้อที่น่าสนใจที่ควรมีผู้ศึกษา และทำงานวิจัย เพื่อสำรวจต่อไปว่าได้สร้างปัญหาในการตีความและทำความเข้าใจของผู้เรียนบ้างหรือไม่ เพียงใด

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Ho. Connie Suk-Han & Fuson. Karen C. (1998). Children's knowledge of teen quantities as tens and ones: Comparisons of Chinese British and American kindergarteners. Journal of Educational Psychology.90 (3).536-544.

Schellenbarger. S. (2014). The Best Language for Math. The Wal Street Journal. Retrieved March 21. 2016, from http://www.wsj.com/articles/the-best-language-for-math-1410304008.