แผนภาพเวนน์ (Venn Diagram) เป็นแผนภาพที่นำเสนอโดยนักคณิตศาสตร์ชาวอังกฤษ ชื่อ John Venn (1834 – 1923) เขาได้เผยแพร่งานของเขาในปี ค.ศ. 1880 เพื่อใช้แสดงความสัมพันธ์เชิงตรรกะระหว่างเซต เป็นแผนภาพที่แสดงทุกความสัมพันธ์ที่เป็นไปได้ทั้งหมดระหว่างเซตต่าง ๆ ที่มีจำนวนจำกัด แผนภาพนี้แทนสมาชิกด้วยจุดในระนาบ และแทนเซตด้วยบริเวณที่อยู่ภายในเส้นโค้งปิด (ปกตินิยมใช้วงกลมหรือวงรีแทนเซต และใช้รูปสี่เหลี่ยมผืนผ้าแทนเอกภพสัมพัทธ์) แผนภาพเวนน์ประกอบด้วยวงกลมหลาย ๆ วงซ้อนทับกัน จุดทั้งหลายในวงกลมที่เขียนกำกับด้วยอักษร S หมายถึง สมาชิกของเซต S ส่วนจุดที่อยู่นอกวงกลมจะแทนสมาชิกที่ไม่อยู่ในเซต S ตัวอย่าง เช่น เซตของสมาชิกทั้งหมดที่เป็นสมาชิกของทั้งเซต S และ T ซึ่งแทนด้วยสัญลักษณ์ S∩T และอ่านว่า “S อินเตอร์เซก T”ที่แทนด้วยพื้นที่ที่มองเห็นด้วยบริเวณที่ซ้อนทับกันระหว่างเซต S และ T

John Venn
ภาพจาก : https://en.wikipedia.org/wiki/John_Venn

   แผนภาพออยเลอร์ (Euler diagram) เป็นแผนภาพที่นำเสนอโดยนักคณิตศาสตร์ชาวสวิตเซอร์แลนด์ชื่อ Leonhard Euler (1707–1783) งานของเขาถูกเผยแพร่ในปี ค.ศ. 1768 แผนภาพเวนน์จะคล้ายกับแผนภาพออยเลอร์มาก ดังนั้นจึงเข้าใจได้ว่า ทำไมคนบางคนจึงสับสนเรื่องความแตกต่างระหว่างแผนภาพเวนน์และแผนภาพออยเลอร์

Leonhard Euler
ที่มา: https://en.wikipedia.org/wiki/Leonhard_Euler

   ในแผนภาพเวนน์ วงกลมต่าง ๆ จะซ้อนทับกันในทุก ๆ ทางที่เป็นไปได้ ส่วนแผนภาพออยเลอร์ไม่จำเป็นต้องแสดงทุกความสัมพันธ์ระหว่างเซต จะแสดงเฉพาะความสัมพันธ์ที่เป็นจริงในชีวิตจริงเท่านั้น ดังนั้นแผนภาพเวนน์จึงเป็นกรณีพิเศษของแผนภาพออยเลอร์ กล่าวคือ ทุกแผนภาพเวนน์เป็นแผนภาพออยเลอร์ แต่ไม่ใช่ทุกแผนภาพออยเลอร์จะเป็นแผนภาพเวนน์

   ตัวอย่าง กรณีที่มี 2 เซตในภาพนี้ เซต A แทนเซตของสัตว์สี่เท้า และเซต B แทนเซตของนก

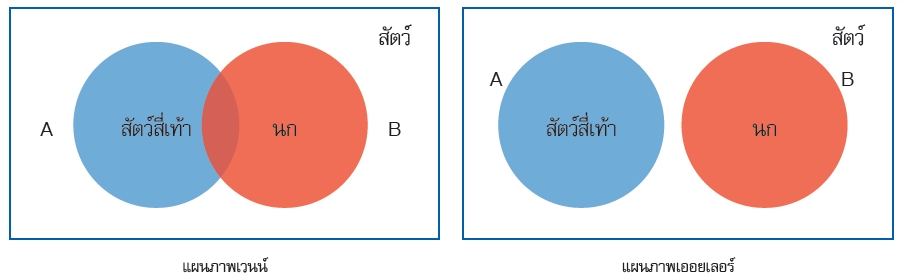
ภาพ 1 ความแตกต่างระหว่างแผนภาพเวนน์กับแผนภาพออยเลอร์

   ในแผนภาพเวนน์แสดงส่วนที่เป็นอินเตอร์เซกชันทั้ง ๆ ที่ไม่มีสมาชิกในชีวิตจริงอยู่ในนั้นก็ตาม นั่นคือ บริเวณที่วงกลม A ตัดกับวงกลม B เป็นเซตว่าง ในทางตรงกันข้ามแผนภาพออยเลอร์วงกลมสองวงไม่ตัดกัน เพราะในโลกแห่งความเป็นจริงไม่มีสัตว์ใดที่มีสี่เท้าและเป็นนกด้วย ในขณะเดียวกัน เมื่อนับจำนวน 2² = 4 บริเวณในแผนภาพเวนน์จะพบว่ามีจำนวนบริเวณทั้งหมดรวมทั้งบริเวณที่อยู่นอกวงกลมทั้งสองวงด้วย

   หมายเหตุ ในกรณีที่ไม่ต้องการเน้นเอกภพสัมพัทธ์ เราอาจละรูปสี่เหลี่ยมผืนผ้าไว้ เช่นในตัวอย่างต่อไปนี้

   ตัวอย่าง กรณีที่มี 3 เซตให้ A = {1, 2, 5}, B = {1, 6} และ C = {4, 7} เขียนอธิบายความสัมพันธ์ระหว่างเซตด้วยแผนภาพได้ดังนี้

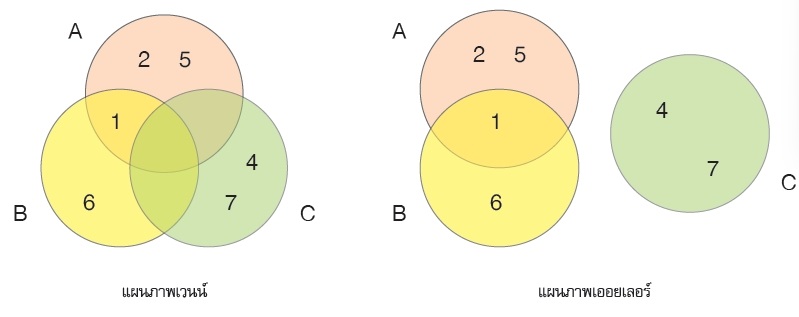
ภาพ 2 ความแตกต่างระหว่างแผนภาพเวนน์กับแผนภาพออยเลอร์

   จำนวนบริเวณในแผนภาพเวนน์ มีทั้งหมด 2³ = 8 บริเวณ รวมทั้งบริเวณที่อยู่นอกวงกลมทั้งสามวงด้วย

   ตัวอย่าง กรณีที่มี 3 เซต ให้ A = {1, 2, 4, 7}, B = {2, 3, 4, 5} และ C = {1, 2, 3, 6} เนื่องจากแต่ละเซตเหล่านี้มีส่วนร่วมกัน ไม่มีบริเวณที่ตัดวงกลมใดเป็นเซตว่าง ดังนั้น ในกรณีนี้แผนภาพออยเลอร์จะเหมือนกับแผนภาพเวนน์ ดังแสดงในภาพ 3

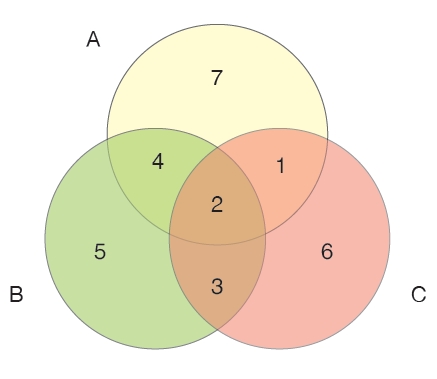
ภาพ 3 แผนภาพออยเลอร์กับแผนภาพเวนน์เหมือนกัน

การนับจำนวนบริเวณในแผนภาพเวนน์

   โดยทั่วไปเราสร้างแผนภาพเวนน์โดยใช้วงกลมที่สมภาคกัน (มีรูปร่างเหมือนกันและขนาดเท่ากัน) ดังเช่นในภาพ 1 - ภาพ 3 ถ้าเราพยายามจัดวงกลม 4 วง ที่สมภาคกัน เพื่อแสดงการตัดกันทั้งหมดที่เป็นไปได้ระหว่างวงกลม 4 วงนี้ จะเห็นว่าทำไม่ได้ แต่ถ้าอนุญาตให้ใช้เส้นโค้งปิดที่ไม่จำเป็นต้อง “สมภาคกัน” จะเห็นว่าเราสามารถเขียนแผนภาพเวนน์ได้ ดังตัวอย่างในภาพ 4

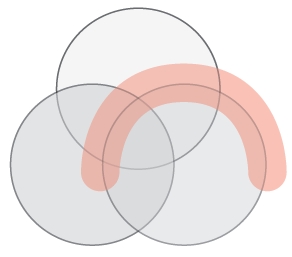
แผนภาพเวนน์ดังภาพใช้วงกลม 3 วงกับเส้นโค้งปิด 1 เส้น

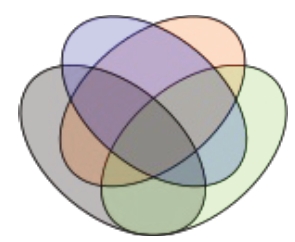
แผนภาพเวนน์ดังภาพใช้เส้นโค้งปิด 4 เส้นที่สมภาคกันแต่ไม่ใช่วงกลมแต่เป็นวงรี

ภาพ 4

   เราได้เห็นแผนภาพเวนน์ใน ภาพ 1 ว่าบริเวณที่เกิดจากวงกลม 2 วง ตัดกันทำให้เกิด 2² = 4 บริเวณ และบริเวณที่เกิดจากวงกลม 3 วง ในภาพ 2 บริเวณที่เกิดจากวงกลม 3 วง ตัดกันทำให้เกิด 2³ = 8 บริเวณ และถ้าเรานับจำนวนบริเวณในแผนภาพเวนน์ที่เกิดจากการตัดกัน ที่เป็นไปได้ทั้งหมดของเส้นโค้งปิด n เส้น จะได้บริเวณทั้งหมด 2ⁿ บริเวณ ดังข้อพิสูจน์ต่อไปนี้

   สมมุติให้ {C₁, C₂, ..., C_n} เป็นเซตของเส้นโค้งปิด n เส้น และให้ x = (x₁, x₂, ..., x_n) แทนบริเวณใดๆ ในแผนภาพเวนน์เมื่อ xi ∈ {Y, N} โดยที่ x_i = Y เมื่อ x เป็นบริเวณที่อยู่ในเส้นโค้งปิด C₁ และ x_i = N เมื่อ x เป็นบริเวณที่ไม่อยู่ใน C_i สำหรับ 1 ≤ i ≤ n จะเห็นว่าแต่ละ x_i มีทางเลือกที่เป็นไปได้สองทางคือ Y หรือ N ดังนั้น จำนวนบริเวณ x = (x₁, x₂, ..., x_n) มีทั้งหมด 2ⁿ บริเวณ

   การคำนวณข้างล่างนี้ แสดงให้เห็นว่าการเขียนแผนภาพเวนน์ทำได้เมื่อใช้วงกลมที่สมภาคกัน 2 วง หรือ 3 วง และไม่สามารถเขียนแผนภาพเวนน์ได้เมื่อใช้วงกลมที่สมภาคกัน n วง เมื่อ n ≥ 4

   ขั้นแรกเราจะนับจำนวนบริเวณที่มากที่สุดในแผนภาพเวนน์ที่เกิดจากวงกลม n วงตัดกัน เพื่อให้ได้จำนวนบริเวณมากที่สุด เราจะกำหนดให้วงกลมสองวงใดๆ ต้องตัดกันที่สองจุดและไม่มีวงกลมมากกว่าสองวงใดๆ ตัดกันที่จุดเดียวกัน เราจะนับโดยใช้สมการเวียนเกิดดังนี้

   ให้ r_n แทนจำนวนบริเวณที่มากที่สุดที่เกิดจากวงกลม n วง ตัดกัน ดังนั้น r_n-1 คือจำนวนบริเวณที่มากที่สุดที่เกิดจากวงกลม n - 1 วง ตัดกัน สมมุติว่ามีแผนภาพเวนน์ที่เกิดจากวงกลม n - 1 วง ตัดกันอยู่ก่อนแล้ว และเราจะเพิ่มวงกลมวงที่ n เข้าไปในแผนภาพเวนน์ที่มีวงกลม n - 1 วงเหล่านั้น เมื่อวงกลมวงที่ n ตัดกับวงกลมวงใด ใน n - 1 วง จะทำให้มีบริเวณเพิ่มขึ้น 2 บริเวณ เพราะเมื่อวงกลมวงที่ n ตัดกับวงกลม C_i ที่เป็นวงใดวงหนึ่งใน n - 1 วง ส่วนของเส้นโค้งของวงกลมวงที่ n ที่อยู่ภายในวงกลม C_i จะแบ่ง C_i ออกเป็นสองบริเวณ นั่นคือทำให้มีบริเวณเพิ่มขึ้น 1 บริเวณ และส่วนโค้งอีกส่วนของวงที่ n ที่อยู่ภายนอกวงกลม C_i จะทำให้บริเวณที่อยู่ภายนอกเพิ่มขึ้นอีก 1 บริเวณ ดังนั้นเมื่อเพิ่มวงกลมวงที่ n จะทำให้มีบริเวณเพิ่มขึ้นอีก 2 บริเวณ แสดงว่าเมื่อเพิ่มวงกลมวงที่ n ไปตัดกับวงกลม n - 1 วง ที่มีอยู่ก่อนแล้วจะทำให้มีบริเวณเพิ่มขึ้นทั้งหมด 2(n - 1) บริเวณ นั่นคือ r_n = r_n-1 + 2_{(n - 1)} ซึ่งเป็นจริงเมื่อ n ≥ 2 และ r₁ = 2 ใช้การแทนค่าไปเรื่อยๆ จะได้ r_n ในรูปของตัวแปร n เพียงตัวเดียว ดังนี้

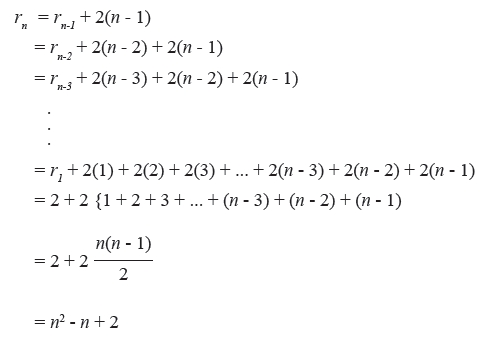
   จะเห็นว่า n² - n + 2 = 2ⁿ เมื่อ n = 1, 2, 3 และ n² - n + 2 < 2ⁿ เมื่อ n ≥ 4 แสดงว่า เราสามารถเขียนแผนภาพเวนน์โดยใช้วงกลมที่สมภาคกันได้ก็ต่อเมื่อ จำนวนวงกลมเหล่านั้นเท่ากับ 1 2 หรือ 3 เท่านั้น

   ทั้งแผนภาพเวนน์และแผนภาพออยเลอร์ถูกใช้เป็นเครื่องมือในการสอนเรื่องเซต ทฤษฎีเซต ตรรกศาสตร์ ภาษาศาสตร์ บริหารธุรกิจ และอื่น ๆ

   คามาลา แฮร์ริส (Kamala Harris) รองประธานาธิบดีของสหรัฐอเมริกาคนปัจจุบัน ตกหลุมรักและหลงใหลในแผนภาพเวนน์เป็นอย่างมาก เธอกล่าวว่าเธอใช้แผนภาพเวนน์ในการอธิบายอะไรได้หลายสิ่งหลายอย่าง นอกจากนี้ เธอยังกล่าวอีกว่าถ้าเผชิญกับปัญหาที่ยุ่งยากซับซ้อนให้เขียนแผนภาพเวนน์จะช่วยให้การแก้ปัญหาง่ายขึ้น

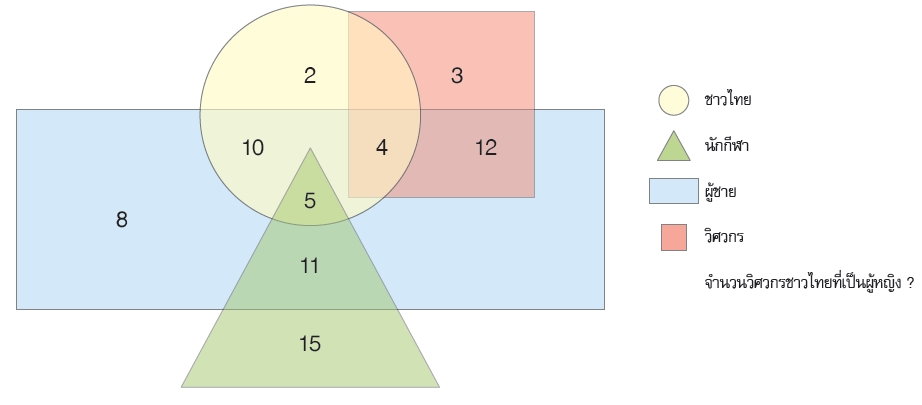
ตัวอย่างการนับบริเวณในภาพ

บรรณานุกรม

Kamala’s Obsession with Venn Diagrams. Retrived October 20, 2022, from https://www.skynews.com.au/opinion/rita-panahi/kamala-harris-apparentlyloves-a-venn-diagram/video/bc8cc574c0b2007c1139530c90c79ebf.

Myers, Amy N. Are Venn Diagrams Limited to Three or Fewer Set ?. Retrived October 20, 2022, from https://images.template.net/wp-content/uploads/2016/02/26060612/ Colourful-Venn-Diagram.pdf.

Venn Diagram. Retrived October 20, 2022, from https://en.wikipedia.org/wiki/John_Venn.