ในปัจจุบันโรคนิ่วในระบบทางเดินปัสสาวะเป็นโรคที่พบได้บ่อย เกิดได้กับทุกเพศทุกวัย แต่จะพบในชายมากกว่าหญิงประมาณ 3 เท่า สำหรับประเทศไทยจะพบคนที่เป็นโรคนิ่วมากในภาคเหนือและภาคอีสาน

   ทางการแพทย์จึงให้ความสำคัญกับการรักษาโรคนี้ และมีการพัฒนาวิธีการรักษาอยู่ตลอดเวลา จนในปัจจุบันมีวิธีการรักษาแบบหนึ่ง ซึ่งเป็นการรักษาจากภายนอกและใช้เวลาพักฟื้นไม่นานนัก แต่สิ่งที่น่าทึ่งคือการรักษาด้วยวิธีนี้ ได้นำความรู้ทางด้านคณิตศาสตร์มาช่วยในกระบวนการดำเนินงานด้วย

   นิ่ว เป็นสิ่งแปลกปลอมที่อยู่ในร่างกายของเรา นิ่วในระบบทางเดินปัสสาวะเกิดจากการตกผลึกของตะกอนในปัสสาวะ เช่น หินปูน (แคลเซียม) ออกซาเลต ฟอสเฟต กรดยูริก และซีสตีน ดังนั้นอวัยวะใดที่ปัสสาวะผ่านในระบบทางเดินปัสสาวะ ดังรูปที่ 1 ก็จะทำให้เกิดนิ่วได้ นิ่วจึงสามารถเกิดได้ทั้งในไต ท่อไต กระเพาะปัสสาวะ และท่อปัสสาวะ

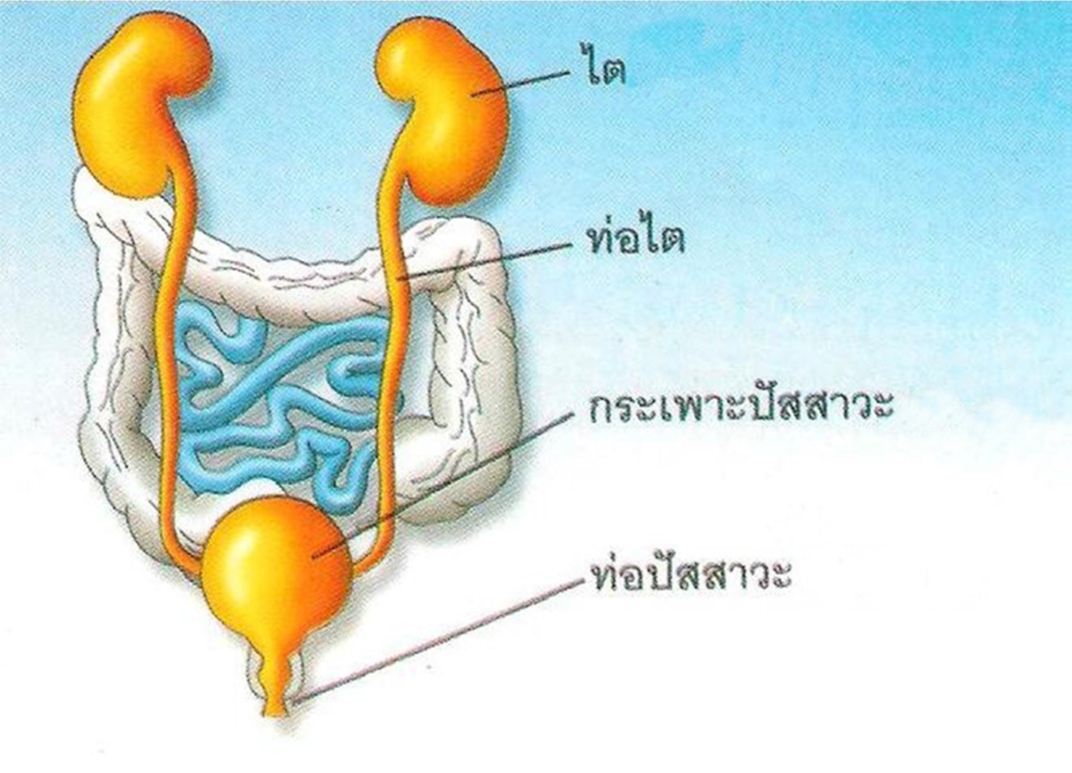
รูปที่ 1 ระบบทางเดินปัสสาวะ
ที่มา: http://bomsand.blogspot.com/2013_01_01_archive.html

   “อั้นฉี่นาน ๆ ระวังเป็นนิ่วนะ” เป็นวลีที่คงจะคุ้นหูตั้งแต่เด็ก เพราะว่าการอั้นปัสสาวะนาน ๆ จะทำให้ตะกอนที่อยู่ในปัสสาวะตกค้างอยู่ในระบบทางเดินปัสสาวะ เมื่อนานเข้าตะกอนก็จะสะสมกันจนเกิดเป็นก้อนนิ่ว นอกจากนั้น เพศ อายุ กรรมพันธุ์ ปริมาณน้ำที่ดื่ม ก็ยังเป็นปัจจัยที่ทำให้เกิดนิ่วได้อีกด้วย

   โดยปกติ นิ่วที่มีขนาดเล็กจะหลุดออกได้เองพร้อมกับปัสสาวะโดยการดื่มน้ำสะอาดมาก ๆ รับประทานยาละลายนิ่ว หรือยาขับปัสสาวะ ในกรณีที่นิ่วมีขนาดใหญ่จนร่างกายไม่สามารถขับออกมาได้ จำเป็นที่จะต้องใช้วิธีการรักษาแบบอื่นที่เรียกว่า lithotripsy และในบทความนี้ จะขอพูดถึงวิธีการรักษาดังกล่าว เนื่องจากเครื่องมือที่ใช้ มีความน่าสนใจทางคณิตศาสตร์ เพราะใช้สมบัติการสะท้อนของวงรีในกระบวนการทำงาน แต่การรักษาด้วยวิธีนี้ จะเหมาะกับนิ่วที่อยู่ในไตและท่อไต และนิ่วจะต้องมีขนาดไม่เกิน 2 เซนติเมตร ถ้านิ่วมีขนาดใหญ่กว่านี้ ต้องใช้วิธีการผ่าตัด

   วงรีมีสมบัติที่มีความสำคัญประการหนึ่ง คือ สมบัติการสะท้อน เช่น ถ้าสร้างทรงรีให้เป็นกระจกที่สะท้อนแสงได้ แล้วแสงจะเดินทางจากโฟกัสหนึ่งของทรงรีไปกระทบกับพื้นผิวของทรงรี จากนั้นจะถูกสะท้อนไปยังโฟกัสที่สองของทรงรี ดังรูปที่ 2

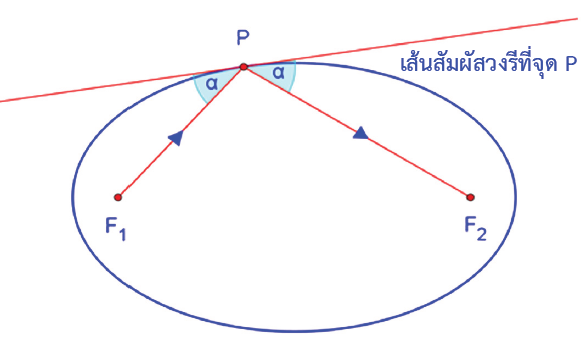
รูปที่ 2 การสะท้อนของวงรี

   สมบัติดังกล่าวอธิบายได้โดยเริ่มจากกฎการสะท้อนของบนเส้นตรง เพราะเมื่อแสงเดินทางไปกระทบกับเส้นตรงแล้ว แสงจะถูกสะท้อนออกมาโดยมุมตกกระทบเท่ากับมุมสะท้อน ดังรูปที่ 3 ทำให้แสดงได้ด้วยว่าระยะทางของแสงที่เดินทางจากจุด R ไปกระทบจุด O แล้วสะท้อนไปยังจุด S เป็นระยะทางที่สั้นที่สุด เมื่อเทียบกับระยะทางที่แสงเดินทางจากจุด R ไปกระทบจุดอื่น ๆ บนเส้นตรง M แล้วสะท้อนไปยังจุด S (อ่านวิธีการพิสูจน์ได้จากหนังสือเพิ่มเติมเสริมศักยภาพการเรียนรู้คณิตศาสตร์มัธยมศึกษาตอนปลาย (ม.4-6) : เรขาคณิตวิเคราะห์)

   จากรูปที่ 2 ถ้าจะแสดงว่าแสงเดินทางจากจุด F₁ ไปกระทบกับพื้นผิวทรงรีที่จุด P แล้วสะท้อนไปยังจุด F₂ ก็เพียงแค่แสดงว่าระยะทางของแสงที่เดินทางจากจุด F₁ ไปกระทบผิวทรงรีที่จุด Pแล้วสะท้อนไปยังจุด F₂ เป็นระยะทางที่สั้นที่สุดเมื่อเทียบกับระยะทางที่แสงเดินทางจากจุด F₁ ไปกระทบจุดอื่น ๆ บนเส้นสัมผัสวงรีที่จุด P แล้วสะท้อนไปยังจุด F₂ ซึ่งสามารถพิสูจน์ได้ ดังนี้

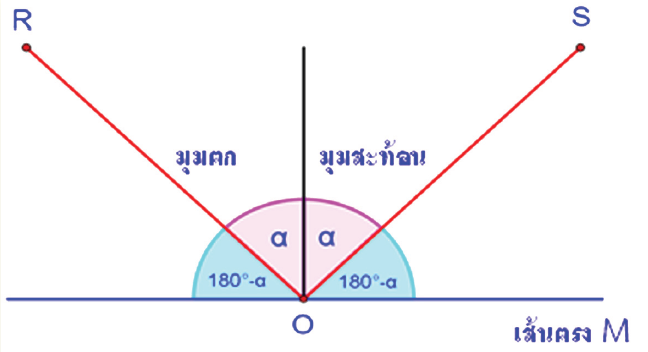
รูปที่ 3 การสะท้อนของแสงบนเส้นตรง

การพิสูจน์ จากรูปที่ 4 ให้ A เป็นจุดใด ๆ บนวงรี สร้างเส้นตรง l ซึ่งเป็นเส้นสัมผัสของวงรีที่จุด A

                                ให้ B เป็นจุดใด ๆ บนเส้นตรง l โดยที่จุด B ไม่ทับจุด A

                                ให้ C เป็นจุดตัดของวงรีกับเส้นตรง BF₂

               จากบทนิยามของวงรี จะได้ว่า

                                F₁C + CF₂ = F₁A + AF₂

               จากอสมการอิงรูปสามเหลี่ยม (triangle inequality) จะได้ว่า

                                F₁B + BC > F₁C

               ดังนั้น        F₁B + BF₂ = F₁B + BC + CF₂ > F₁C + CF₂ = F₁A + AF₂

               จะได้ว่าจุด A เป็นจุดบนเส้นตรง l ที่ทำให้ระยะทางของแสงที่เดินทางจาก F₁ ไปตกกระทบเส้นตรง l  แล้วสะท้อนไปยัง F₂ เป็นระยะทางที่สั้นที่สุด จากหลักการสะท้อนแสงบนเส้นตรงที่ได้กล่าวมา จะได้ว่ามุมตกกระทบเท่ากับมุมสะท้อน ดังนั้นแสงที่เดินทางจากโฟกัสหนึ่งของทรงรีไปกระทบกับพื้นผิวของทรงรีจะถูกสะท้อนไปยังอีกโฟกัสหนึ่งของทรงรีเสมอ

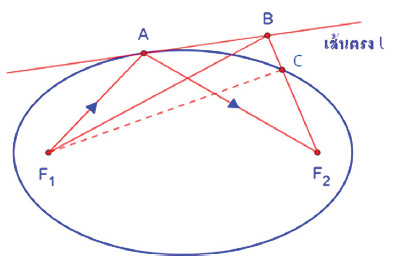
รูปที่ 4

   สมบัติการสะท้อนนี้ไม่ได้เป็นจริงสำหรับแสงเท่านั้น แต่ยังเป็นจริงสำหรับคลื่นเสียงด้วย และสมบัตินี้เองที่ถูกนำไปใช้เป็นกระบวนการทำงานของเครื่องสลายนิ่ว (Extracorporeal Shock Wave Lithotripsy/ESWL machine) โดยเครื่องสลายนิ่วถูกออกแบบให้มีลักษณะเป็นรูปครึ่งทรงรี และมีแหล่งกำเนิดคลื่นเสียงความถี่สูงอยู่ในตำแหน่งโฟกัสที่หนึ่งของทรงรี การสลายนิ่วด้วยเครื่องนี้ จะเลื่อนเครื่องสลายนิ่วเข้าไปใกล้ตัวผู้ป่วยจนตำแหน่งโฟกัสที่สองของทรงรีตรงกับตำแหน่งของนิ่ว เมื่อปล่อยคลื่นเสียงความถี่สูงออกจากแหล่งกำเนิดคลื่นเสียงตรงตำแหน่งโฟกัสที่หนึ่ง คลื่นเสียงก็จะเคลื่อนที่ไปกระทบกับผิวของทรงรี จากสมบัติการสะท้อนของทรงรี ไม่ว่าคลื่นเสียงไปกระทบที่ส่วนไหนของทรงรีก็ตาม คลื่นจะถูกสะท้อนไปยังจุดโฟกัสที่สองเสมอ นั่นคือตำแหน่งของนิ่วดัง รูปที่ 5 ดังนั้นตำแหน่งของนิ่วจึงเป็นจุดรวมของคลื่นเสียงที่ถูกสะท้อนจากทรงรีทุกทิศทุกทาง ซึ่งทำให้เกิดการสั่นสะเทือนที่ก้อนนิ่ว และทำให้ก้อนนิ่วแตกเป็นชิ้นเล็ก ๆ ในที่สุด โดยจะใช้เวลาในการรักษาประมาณ 1 ชั่วโมง จากนั้นร่างกายก็จะขับก้อนนิ่วที่แตกเป็นชิ้นเล็ก ๆ ออกมาทางปัสสาวะ

   เครื่องสลายนิ่วเป็นเครื่องมือที่ใช้ภายนอกร่างกาย ดังนั้นผู้ป่วยที่รักษาด้วยวิธีนี้ จะไม่ได้รับความเจ็บปวดมากนัก และสามารถกลับบ้านได้ภายใน 1 วัน ด้วยเหตุนี้วิธีการรักษานิ่วโดยใช้เครื่องสลายนิ่วจึงเป็นที่นิยมอย่างแพร่หลาย

   ไม่เพียงแต่วงรีเท่านั้น รูปเรขาคณิตอื่น ๆ ก็มีสมบัติ ซึ่งสามารถนำมาประยุกต์ใช้เพื่อช่วยในการแก้ปัญหาต่าง ๆ หรือช่วยในการพัฒนาเทคโนโลยีใหม่ ๆ ได้ เช่น การใช้สมบัติของพาราโบลาในการสร้างจานรับส่งสัญญาณ การใช้สมบัติของไฮเพอร์โบลาในการสร้างกล้องโทรทรรศน์ชนิดสะท้อนแสง ดังนั้นการจัดการเรียนรู้ให้ผู้เรียนได้ศึกษาคณิตศาสตร์จากชีวิตจริงจะช่วยให้ผู้เรียนมองเห็นประโยชน์ในการเรียนคณิตศาสตร์มากขึ้น อีกทั้งยังช่วยพัฒนาศักยภาพของผู้เรียนในการแก้ปัญหาที่เกิดขึ้นในชีวิต และเตรียมความพร้อมให้แก่ผู้เรียนสำหรับการทำงานในอนาคต

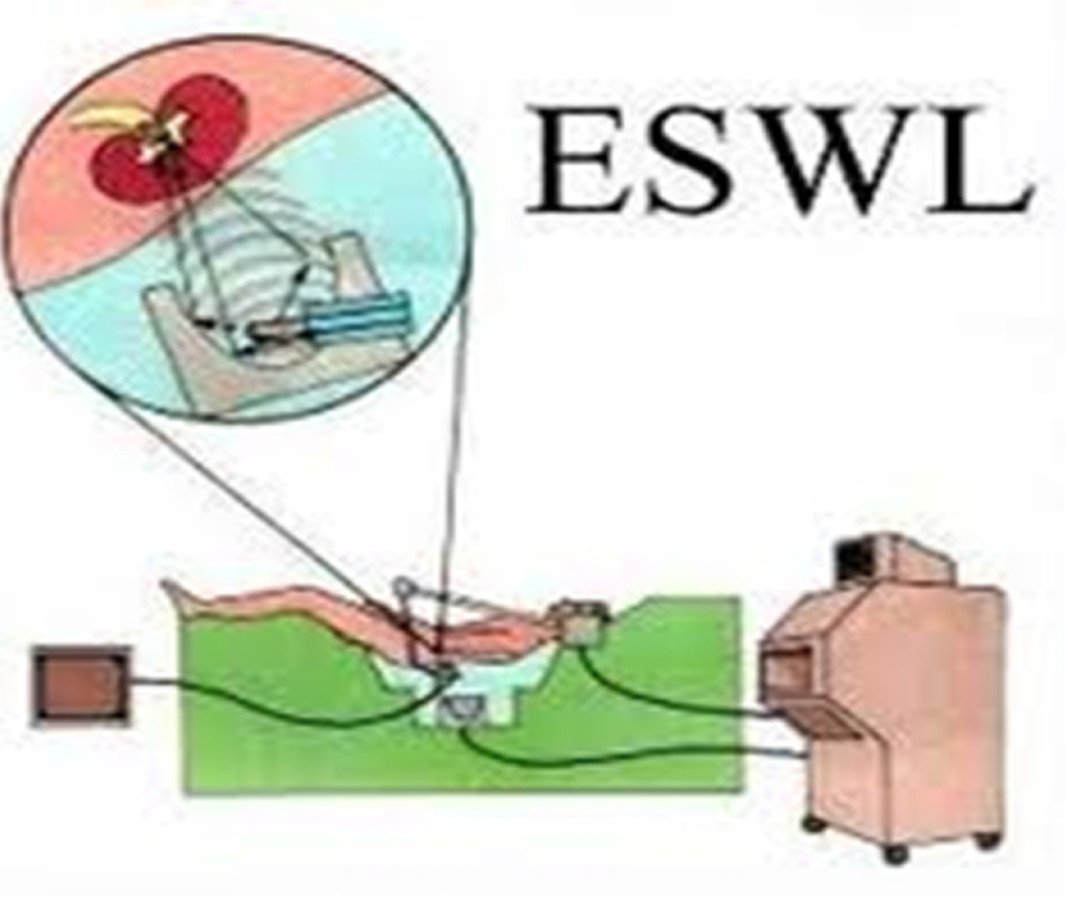
รูปที่ 5 เครื่องสลายนิ่ว (ESWL)
ที่มา: http://bme240.eng.uci.edu/students/09s/ysantoro/CurrTechn.html

บรรณานุกรม

Natasha Glydon. Lithotripsy – A Medical Application of theEllipse. สืบค้นเมื่อ 20 มกราคม 2557, จาก http://mathcentral.uregina.ca/beyond/articles/Lithotripsy/lithotripsy1.html

วิสูตร คงเจริญสมบัติ. (2557). อาการและการรักษานิ่วในระบบทางเดินปัสสาวะ. สืบค้นเมื่อ 20 มกราคม 2557, จาก http://www.prostate-rama.com/reading_detailphp?cid=5

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ(2557). หนังสือเพิ่มเติมเสริมศักยภาพการเรียนรู้คณิตศาสตร์มัธยมศึกษาตอนปลาย (ม.4-6) : เรขาคณิตวิเคราะห์ กรุงเทพมหานคร:สถาบันพัฒนาคุณภาพวิชาการ.