ภาคตัดกรวยเป็นเนื้อหาหนึ่งในเรื่องเรขาคณิตวิเคราะห์ โดยการศึกษาเกี่ยวกับภาคตัดกรวยได้เริ่มต้นมานานแล้ว ผู้หนึ่งที่ศึกษาเกี่ยวกับภาคตัดกรวยและค้นพบสมบัติที่น่าสนใจบางประการของภาคตัดกรวย คือ อะพอลโลเนียสแห่งเพอร์กา (Apollonius of Perga) เขาได้เขียนตำราเกี่ยวกับภาคตัดกรวยไว้มากมาย ภาคตัดกรวยสามารถนำไปใช้ประโยชน์ได้หลากหลายด้าน เช่น การออกแบบจานรับส่งสัญญาณในระบบโทรคมนาคม การออกแบบอุปกรณ์ทางการแพทย์ที่อาศัยการสะท้อนของคลื่นเสียง การออกแบบสิ่งก่อสร้างเพื่อกักเก็บพลังงานแสงอาทิตย์เพื่อนำไปใช้ในการผลิตไฟฟ้า การผลิตกล้องโทรทรรศน์ชนิดสะท้อนแสง

หลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551 (ฉบับปรับปรุง พ.ศ. 2560) ได้กำหนดให้ภาคตัดกรวยเป็นส่วนหนึ่งในสาระการเรียนรู้เพิ่มเติมเรื่องเรขาคณิตวิเคราะห์ สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี (สสวท.) ได้จัดเนื้อหาเรื่องภาคตัดกรวยไว้ในหนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ชั้นมัธยมศึกษาปีที่ 4 เล่ม 2 และได้อธิบายว่า "ภาดตัดกรวยคือ รูปในระนาบที่เกิดจากการตัดกันของระนาบกับกรวย" โดยในที่นี้ กรวย คือ ผิวที่เกิดจากการหมุนเส้นตรงเส้นที่หนึ่งรอบเส้นตรง เส้นที่สองที่ตรึงอยู่กับที่ โดยเส้นตรงทั้งสองเส้นนี้ตัดกันที่จุดจุดหนึ่งและทำมุมแหลมต่อกัน เรียกกรวยในลักษณะนี้อีกชื่อหนึ่งว่า "กรวยกลมตรง" และเรียกจุดตัดระหว่างเส้นตรงทั้งสองเส้นว่า "จุดยอด"

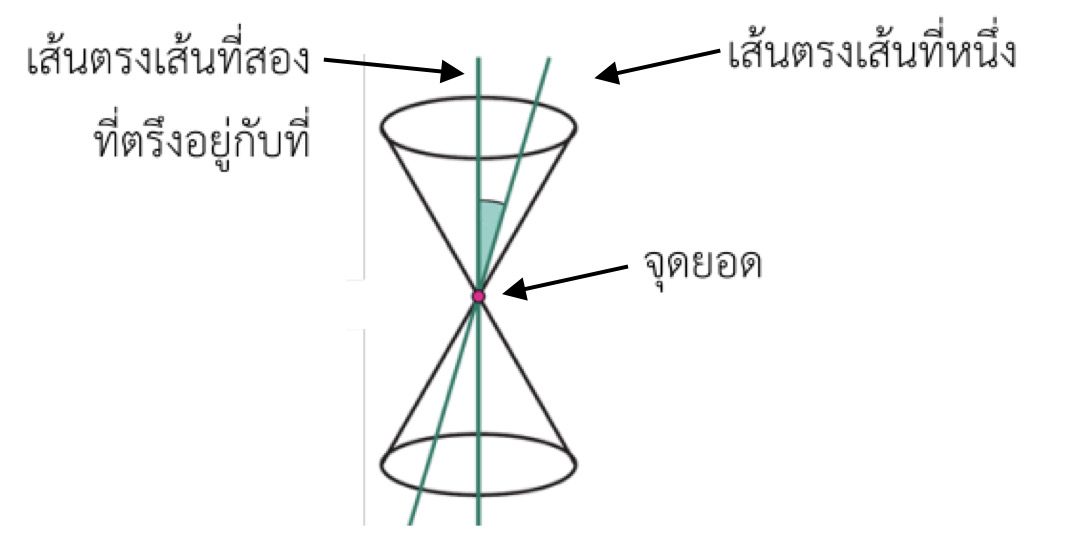
ภาพ 1 กรวย
ที่มา : หนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 4 เล่ม 2 ของ สสวท.

การตัดกันของระนาบกับกรวยสามารถแบ่งออกเป็น 2 กรณี ได้แก่ กรณีที่ 1 ระนาบและกรวยตัดกันโดยไม่ผ่านจุดยอดของกรวย จะได้ภาคตัดกรวยที่เรียกว่า วงกลม วงรี พาราโบลา และไฮเพอร์โบลา ดังภาพ 2

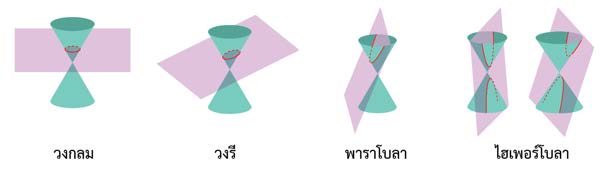
ภาพ 2 แสดงภาคตัดกรวยกรณีที่ระนาบและกรวยตัดกัน โดยไม่ผ่านจุดยอดของกรวย
ที่มา : หนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 4 เล่ม 2 ของ สสวท.

และกรณีที่ 2 ระนาบและกรวยตัดกัน โดยผ่านจุดยอดของกรวย เรียกรูปที่ได้จากการตัดในลักษณะนี้ว่า "ภาคตัดกรวยลดรูป" ซึ่งอาจจะ ได้เป็น จุด 1 จุด เส้นตรง 1 เส้น หรือเส้นตรง 2 เส้นตัดกัน ดังภาพ 3

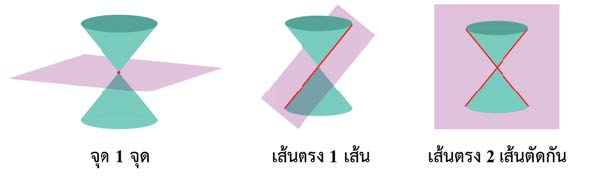
ภาพ 3 แสดงภาคตัดกรวยกรณีที่ระนาบและกรวยตัดกัน โดยผ่านจุดยอดของกรวย
ที่มา : หนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 4 เล่ม 2 ของ สสวท.

บทความนี้จะกล่าวถึงเฉพาะกรณีระนาบและกรวยตัดกันโดยไม่ผ่านจุดยอดของกรวย และเพื่อให้ผู้เรียนสามารถจดจำความรู้เนื้อหาที่เรียนได้อย่างยาวนาน เกิดความคงทนในการเรียนรู้ สามารถนำความรู้ที่ได้รับไปปรับใช้กับสถานการณ์ต่างๆ ที่แตกต่างจากตัวอย่างและแบบฝึกหัดในหนังสือเรียนได้ ผู้เรียนควรได้ทบทวนความรู้ ความเข้าใจในเนื้อหาจากการฝึกปฏิบัติหรือจากการทำกิจกรรม เพื่อให้เกิดความเข้าใจอย่างถ่องแท้ ผู้เขียนขอแนะนำสื่อการเรียนรู้ CsC (Conic sections Circle) เป็นตัวเลือกหนึ่งในการทบทวน ความรู้ความเข้าใจเกี่ยวกับภาคตัดกรวยในส่วนของวงกลม โดยสื่อการเรียนรู้ CsC จัดทำขึ้นโดยโปรแกรมสำเร็จรูป GeoGebra

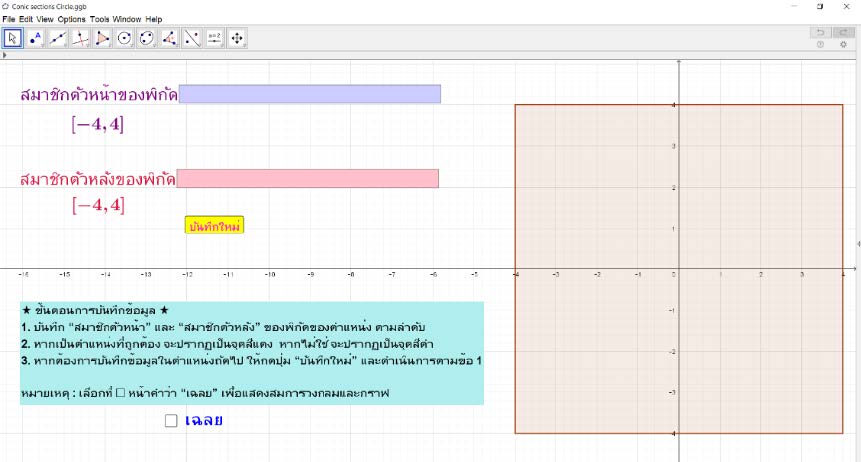
ภาพ 4 แสดงหน้าจอสื่อการเรียนรู้ CsC

ทั้งนี้ สามารถทดลองใช้สื่อการเรียนรู้ CsC ได้ที่ https://www.geogebra.org/m/gbndetjd โดยสื่อการเรียนรู้ CsC มีส่วนประกอบสำคัญ 3 ส่วน ดังนี้

          ส่วนที่ 1 (มุมซ้ายบนของหน้าจอสื่อ) แสดง "ช่องบันทึกสมาชิกตัวหน้าของพิกัด" และ "ช่องบันทึกสมาชิกตัวหลังของพิกัด" และปุ่ม "บันทึกใหม่" ดังภาพ 5

ภาพ 5 หน้าจอส่วนที่ 1 ของสื่อการเรียนรู้ CsC

          ส่วนที่ 2 (มุมซ้ายล่างของหน้าจอสื่อ) แสดง "ขั้นตอนการบันทึกข้อมูล" และปุ่ม "เฉลย" ดังภาพ 6

ภาพ 6 หน้าจอส่วนที่ 2 ของสื่อการเรียนรู้ CsC

          ส่วนที่ 3 (ด้านขวาของหน้าจอสื่อ) บริเวณแสดงคู่อันดับที่เป็นพิกัดของตำแหน่ง สมการวงกลมและกราฟ ดังภาพ 7

ภาพ 7 หน้าจอส่วนที่ 3 ของสื่อการเรียนรู้ CsC

จะนำสื่อการเรียนรู้ CsC ไปจัดกิจกรรมการเรียนรู้ได้อย่างไร
ตัวอย่างขั้นตอนการจัดกิจกรรมการเรียนรู้โดยใช้สื่อการเรียนรู้ CsC
          ขั้นตอนที่ 1 อ่านสถานการณ์ที่กำหนดให้ต่อไปนี้
          กองกำลังเรือดำน้ำประกอบด้วยเรือดำน้ำจำนวน 5 ลำ ได้แก่ เรือลูกจำนวน 4 ลำ และอีกหนึ่งลำคือเรือดำน้ำหลัก โดยมีเงื่อนไขการวางกำลังดังนี้
                - เรือลูกแต่ละลำวางตัวอยู่บนเส้นรอบวงของวงกลม ซึ่งพิกัดของตำแหน่งของเรือลูกแต่ละลำแสดงด้วยคู่อันดับ โดยที่สมาชิกตัวหน้าและสมาชิกตัวหลังของคู่อันดับเป็นจำนวนเต็มที่มีค่าตั้งแต่ -4 ถึง 4
                - เรือดำน้ำหลักอยู่ที่จุดศูนย์กลางของวงกลม
          ภารกิจของนักเรียนคือออกคำสั่งยิงขีปนาวุธ โดยกำหนดพิกัดของตำแหน่งที่จะปล่อยขีปนาวุธเพื่อทำลายกองกำลังเรือดำน้ำของข้าศึก และใช้ขีปนาวุธน้อยที่สุด
          อาจใช้การถาม - ตอบ เพื่อทบทวนข้อมูลสำคัญของสถานการณ์ ดังนี้
                - ภารกิจคืออะไร (คำตอบ: ทำลายกองกำลังเรือดำนำของข้าศึก และใช้ขีปนาวุธน้อยที่สุด)
                - ข้าศึกจัดกองกำลังเรือดำน้ำมาทั้งหมดกี่ลำ (คำตอบ: 5 ลำ)
                - ข้าศึกจัดวางกองกำลังเรือดำน้ำในรูปแบบใด (คำตอบ: วงกลม)
                - มีเงื่อนไขการจัดวางเรือดำน้ำแต่ละลำอย่างไร (แนวคำตอบ: เรือดำน้ำ 4 ลำ วางตัวอยู่บนเส้นรอบวงของวงกลม และ เรือดำน้ำอีกหนึ่งลำอยู่ที่จุดศูนย์กลางของวงกลม)
                - ยกตัวอย่างคำสั่งยิงที่คาดว่าเป็นไปได้ที่จะเป็นตำแหน่งของกองเรือดำน้ำของข้าศึก (แนวคำตอบ: (0, 0), (1, -4), (-2, 3) หรือ (-3, -1))
                - สรุปคำสั่งยิงที่ถูกต้อง จะต้องมีสมบัติอย่างไร (คำตอบ: สมาชิกตัวหน้าและตัวหลังของคู่อันดับที่เป็นพิกัดของตำแหน่งของกองกำลังเรือดำน้ำแต่ละลำต้องเป็นจำนวนเต็ม โดยมีค่าตั้งแต่ -4 ถึง 4)

          ขั้นตอนที่ 2 พิมพ์สมาชิกตัวหน้าของคู่อันดับที่เป็นพิกัดของตำแหน่งลงในช่องบันทึกสมาชิกตัวหน้าของพิกัด (ในหน้าจอของสื่อ ส่วนที่ 1) โดยต้องเป็นจำนวนเต็ม และมีค่าตั้งแต่ -4 ถึง 4

          ขั้นตอนที่ 3 พิมพ์สมาชิกตัวหลังของคู่อันดับที่เป็นพิกัดของตำแหน่ง ลงในช่องบันทึกสมาชิกตัวหลังของพิกัด (ในหน้าจอของสื่อ ส่วนที่ 1) โดยต้องเป็นจำนวนเต็ม และมีค่าตั้งแต่ -4 ถึง 4

          ขั้นตอนที่ 4 กดปุ่ม Enter บนแป้นพิมพ์ หากเป็น
                - ตำแหน่งที่ถูกต้องตามเงื่อนไข จะปรากฎเป็นจุดสีแดงในบริเวณแสดงคู่อันดับ (ในหน้าจอของสื่อ ส่วนที่ 3)
                - ตำแหน่งที่ไม่ถูกต้องตามเงื่อนไข จะปรากฎเป็นจุดสีดำในบริเวณแสดงคู่อันดับ (ในหน้าจอของสื่อ ส่วนที่ 3)

          ขั้นตอนที่ 5 ถ้าต้องการบันทึกข้อมูลพิกัดของตำแหน่งถัดไป ให้กดปุ่ม "บันทึกใหม่" (ในหน้าจอของสื่อ ส่วนที่ 1) แล้วดำเนินการ ตามขั้นตอนที่ 2 - 4

          ขั้นตอนที่ 6 ทำนายหรือคาดการณ์สมการวงกลมจากผลลัพธ์ที่ได้

          ขั้นตอนที่ 7 ตรวจสอบความถูกต้องของสมการวงกลม โดยกดปุ่ม "เฉลย" (ในหน้าจอของสื่อ ส่วนที่ 2)

หมายเหตุ หากต้องการเริ่มจัดกิจกรรมการเรียนรู้     ใหม่ ให้กด Ctrl + F

ทั้งนี้ สามารถปรับสมการวงกลมในสื่อการเรียนรู้ CsC ได้ โดยปรับที่ค่าของ h, k และ r ใน Algebra View ของโปรแกรมมสำเร็จรูป GeoGebra ซึ่งสมการวงกลมจะมีจุดศูนย์กลางอยู่ที่ (h, k) และรัศมียาว r หน่วย ต่อไปจะขอยกตัวอย่างสิ่งที่จะปรากฏบนสื่อการเรียน     รู้ CsC เมื่อมีการจัดกิจกรรมตามขั้นตอนที่กล่าวมาข้างต้น เมื่อมีนักเรียน 3 คน คือ นักเรียน A นักเรียน B และนักเรียน C ใช้สื่อการเรียนรู้ CsC ร่วมกัน ดังนี้

จากตัวอย่างการจัดกิจกรรมการเรียนรู้โดยใช้สื่อการเรียนรู้ CsC ข้างต้น จะพบว่า

          นักเรียน A เมื่อได้คู่อันดับที่เป็นตำแหน่งที่ถูกต้อง 2 คู่อันดับแล้ว ก็ได้ทำนายสมการวงกลมทันที โดยให้คู่อันดับ (1,0) เป็นจุดศูนย์กลางของวงกลม และคู่อันดับ (1,-2) เป็นจุดที่วงกลมผ่าน ซึ่งการคาดการณ์จากข้อมูลในลักษณะเช่นนี้ เป็นเพียงรูปแบบหนึ่งที่อาจจะเป็นไปได้เท่านั้น ซึ่งผลก็ปรากฏว่าสมการวงกลมที่นักเรียน A ทำนายไว้ไม่ถูกต้อง

          สำหรับนักเรียน B ได้คาดการณ์คู่อันดับที่เป็นพิกัดของตำแหน่งอีกหนึ่งคู่และเป็นตำแหน่งที่ถูกต้อง แล้วจึงทำนายสมการวงกลม โดยให้คู่อันดับ (1,-2) เป็นจุดศูนย์กลางของวงกลม และคู่อันดับที่เหลืออีกสองอันดับคือ คู่อันดับ (1, 0) และคู่อันดับ (3,-2) เป็นจุดบนวงกลม ซึ่งจุดทั้งสองห่างจากจุดศูนย์กลางของวงกลมเป็นระยะทางเท่ากับรัศมีของวงกลม ซึ่งการคาดการณ์จากข้อมูลในลักษณะเช่นนี้ พบว่ามีเพียงรูปแบบเดียวที่เป็นไปได้ จึงทำให้สมการวงกลมที่นักเรียน B ทำนายไว้ถูกต้อง

          จากตัวอย่างนี้จะเป็นการเพิ่มประสบการณ์ให้แก่นักเรียนว่า การจะทำนายสมการวงกลมนั้นจะต้องมีข้อมูลที่จำเป็น เพียงพอและถูกต้อง จึงจะสามารถทำนายสมการวงกลมได้ถูกต้อง

          ทั้งนี้ ผู้ที่นำสื่อการเรียนรู้ CsC ไปใช้สามารถสร้างสถานการณ์หรือกำหนดรูปแบบ กฎ กติกา รวมทั้งกำหนดเกณฑ์การ คิดคะแนนเพื่อให้เกิดความสนุกสนานหรือความท้าทายแก่ผู้เล่นเพิ่มเติมได้ เช่น การนำไปใช้ในกิจกรรมกลุ่ม โดยให้แต่ละกลุ่มระบุ สมาชิกตัวหน้าและสมาชิกตัวหลังของคู่อันดับที่เป็นพิกัดของตำแหน่ง และครูผู้สอนเป็นผู้บันทึกข้อมูลที่แต่ละกลุ่มระบุ และจะเปลี่ยนเป็นกลุ่มถัดไปให้ข้อมูล เมื่อข้อมูลที่ระบุของกลุ่มนั่นทำให้เกิดเป็นจุดสีดำ แต่ถ้าเป็นจุดสีแดง กลุ่มเดิมยังสามารถระบุข้อมูลต่อได้ หรือบอก สมการวงกลมก็ได้ ทั้งนี้ อาจมีกติกาเพิ่มเติมว่าจะบอกสมการวงกลมได้ก็ต่อเมื่อทราบพิกัดของตำแหน่ง (ปรากฏจุดสีแดง) อย่างน้อย 3 จุด และสามารถบอกได้ทั้งรูปแบบมาตรฐานของสมการวงกลมหรือรูปแบบทั่วไปของสมการวงกลม โดยอาจกำหนดการคิดคะแนน เป็นดังนี้ 
          - กลุ่มที่ให้ข้อมูลพิกัดของตำแหน่งได้ถูกต้อง (ได้จุดสีแดง) จะได้จุดละ 1 คะแนน
          - กลุ่มที่ระบุสมการวงกลมได้ถูกต้อง จะได้ 2 คะแนน จากนั้นคำนวณคะแนนรวมทั้งหมดของแต่ละกลุ่ม โดยกลุ่มที่มีคะแนนรวมมากที่สุดเป็นกลุ่มชนะ ทั้งนี้ อาจกำหนดจำนวนรอบของการเล่นด้วยก็ได้ และก่อนเล่นเกมควรอธิบายกฎ กติกา เกณฑ์การคิดคะแนนให้ผู้เล่นทุกคนเข้าใจตรงกัน
          นอกจากสื่อการเรียนรู้ CsC ซึ่งเป็นสื่อเพื่อใช้ในการทบทวนความรู้ความเข้าใจเรื่องวงกลมแล้ว ผู้เขียนยังได้พัฒนา สื่อการเรียนรู้อีก 2 ชิ้น ที่จัดทำขึ้นโดยโปรแกรมสำเร็จรูป GeoGebra เพื่อใช้ในการทบทวนความรู้ความเข้าใจเกี่ยวกับเรื่องวงรีและ เรื่องไฮเพอร์โบลา ดังนี้
          - สื่อการเรียนรู้ CsE (Conic sections Ellipse) ใช้ในการทบทวนความรู้ความเข้าใจเกี่ยวกับเรื่องวงรี โดยสามารถทดลอง ใช้สื่อได้ที่ https://www.geogebra.org/m/mtsnqquq

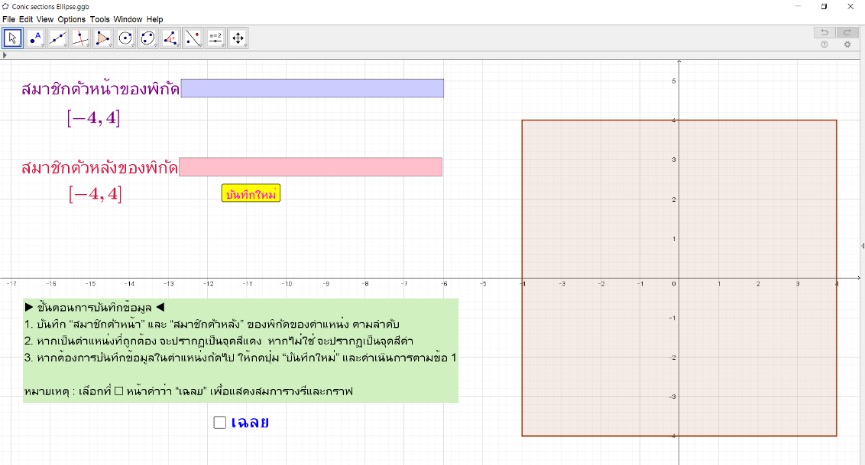
ภาพ 8 หน้าจอสื่อการเรียนรู้ CsE

สมการวงรีในสื่อการเรียนรู้นี้จะอยู่ในรูป \[ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 \] และสามารถปรับรูปแบบของวงรีได้ด้วยการปรับที่ค่าของ h, k, a และ b ใน Algebra View ของโปรแกรมสำเร็จรูป GeoGebra
          - สื่อการเรียนรู้ CsH (Conic sections Hyperbola) ใช้ในการทบทวนความรู้ความเข้าใจเกี่ยวกับเรื่องไฮเพอร์โบลา โดยสามารถ ทดลองใช้สื่อได้ที่ https://www.geogebra.org/m/sdhab97j

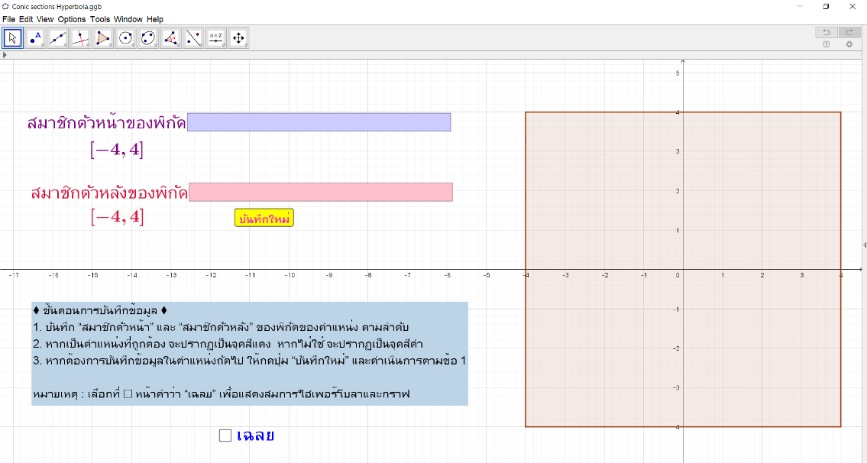
ภาพ 9 หน้าจอสื่อการเรียนรู้ CsH

สมการไฮเพอร์โบลาในสื่อการเรียนรู้นี้จะอยู่ในรูป \[\frac{\text{cofx2} (x-h)^2}{a^2} + \frac{\text{cofy2} (y-k)^2}{b^2} = 1\] และสามารถปรับรูปแบบของไฮเพอร์โบลา ได้ด้วยการปรับที่ค่าของ cofx2, h, k, a และ b ใน Algebra View ของโปรแกรมสำเร็จรูป GeoGebra

หมายเหตุ cofx2 มีค่าเป็น 1 หรือ -1 และ cofy2 = -coix2

(cofx2 และ cofy2 เป็นสัมประสิทธิ์หน้า x และ y โดยที่
          - ถ้า cofx2 = 1 และ cofy2 = -1 ไฮเพอร์โบลาที่ได้เป็นไฮเพอร์โบลาที่มีแกนตามขวางอยู่ในแนวนอน
          - ถ้า cofx2 = -1 และ cofy2 = 1 ไฮเพอร์โบลาที่ได้เป็นไฮเพอร์โบลาที่มีแกนตามขวางอยู่ในแนวตั้ง)

จะเห็นได้ว่า การที่ผู้เรียนได้ทบทวนเนื้อหาอย่างสม่ำเสมอ ไม่ว่าจะด้วยการฝึกปฏิบัติ การฝึกฝนจากการทำแบบฝึกหัด หรือการนำความรู้ที่ได้รับไปปรับใช้กับสถานการณ์ต่างๆ จะทำให้ผู้เรียนมีความรู้ความเข้าใจในเนื้อหาสาระนั้นมากขึ้นและความรู้นั้นจะคงทนอยู่กับผู้เรียนตลอดไป โดยครูมีส่วนสำคัญอย่างยิ่งในการจัดการเรียนรู้ จัดกิจกรรม รวมทั้งสร้างสื่อหรือเครื่องมือที่ดึงดูดใจ เพื่อเปิดโลกการเรียนรู้ของนักเรียนให้กว้างไกลมากยิ่งขึ้น สิ่งเหล่านี้จะส่งผลโดยตรงต่อตัวผู้เรียนทำให้ผู้เรียนมีการเปลี่ยนแปลงพฤติกรรม เปลี่ยนแปลง วิธีการเรียนรู้ ทำให้เกิดความอยากรู้อยากเห็นมากยิ่งขึ้นและมีความคงทนในการเรียนรู้ อีกทั้งยังช่วยให้เกิดความตระหนัก มองเห็นประโยชน์และคุณค่าของการเรียนวิชาคณิตศาสตร์อย่างแท้จริง

บรรณานุกรม

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2563). หนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 4 เล่ม 2 ตามผลการเรียนรู้ กลุ่มสาระการเรียนรู้คณิตศาสตร์ (ฉบับปรับปรุง พ.ศ.2560) ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551. พิมพ์ครั้งที่ 2 กรุงเทพมหานคร จุฬาลงกรณ์มหาวิทยาลัย.