“ภาคตัดกรวย” ได้มาจากการ “ตัดกรวย” จริง กล่าวคือถ้าต่อกรวยกลมตรงสองชิ้นโดยหันจุดยอดเข้าหากันแล้วตัดกรวยในแนวต่าง ๆ ด้วยระนาบ รอยตัดที่ได้จะแตกต่างกันไปดังรูปที่ 1 ดังนั้น ภาคตัดกรวย (conic section หรือ conic) ในทางคณิตศาสตร์ จึงหมายถึงเส้นโค้งที่ได้จากการตัดกรวยกลมตรงด้วยระนาบที่ไม่ผ่านจุดยอดของกรวย เรียกเส้นโค้งที่ได้จากการตัดว่า วงกลม วงรี พาราโบลา และไฮเพอร์โบลา

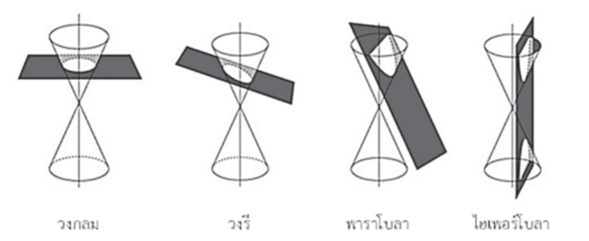
รูปที่ 1 แสดงภาคตัดกรวย
ที่มา: สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี

   การศึกษาเกี่ยวกับภาคตัดกรวยเริ่มมานานแล้ว โดยเส้นโค้งที่เกิดขึ้นไม่เพียงให้ความสวยงามเท่านั้น แต่สามารถนำไปใช้ประโยชน์ได้หลายอย่างเช่น ใน   พ.ศ. 2133 ( ค.ศ. 1590) กาลิเลโอพบว่า ขีปนาวุธที่ยิงขึ้นจากพื้นดินด้วยมุมที่กำหนดมีวิถีการเคลื่อนที่เป็นพาราโบลา ใน   พ.ศ. 2152 ( ค.ศ. 1609) โยฮันส์  เคปเลอร์ พบว่าดาวเคราะห์แต่ละดวงโคจรรอบดวงอาทิตย์เป็นวงรี โดยมีดวงอาทิตย์เป็นโฟกัสจุดหนึ่ง ปัจจุบันจึงได้มีการศึกษาและนำสมบัติต่าง ๆ ของภาคตัดกรวยไปใช้ประโยชน์ในชีวิตจริงเพิ่มมากขึ้น เช่นในอุตสาหกรรมยานยนต์ได้มีการออกแบบล้อของยานพาหนะเป็นวงกลมที่มีผลต่อการเคลื่อนที่ของยานพาหนะ การออกแบบตัวถังหรือส่วนประกอบของยานพาหนะให้มีหน้าตัดเป็นวงรีเพื่อลดระดับจุดศูนย์ถ่วงลงและลดความเสี่ยงในการพลิกคว่ำหรือการกระแทกซึ่งก่อให้เกิดอุบัติเหตุตามมา หรือการออกแบบไฟหน้าของยานพาหนะที่ต้องอาศัยความรู้เรื่องพาราโบลา ดังแสดงในรูปที่ 2

รูปที่ 2 แสดงการนำสมบัติของภาคตัดกรวยมาใช้ออกแบบด้านอุตสาหกรรมยานยนต์
ที่มา: http://www.autoyim.com/260646, http://img.tarad.com/shop/a/asiatrailer/img-lib/spd_20100215145724_b.jpg และ http://www.myfirstbrain.com/student_view.aspx?ID=88460

   อย่างไรก็ตาม หลายคนอาจจะนึกภาพไม่ออกว่าสามารถนำสมบัติของไฮเพอร์โบลาไปใช้ประโยชน์ดังเช่นกรณีของวงกลม วงรีหรือพาราโบลาได้หรือไม่ ดังนั้นในบทความนี้จะขอพูดถึงการนำสมบัติของไฮเพอร์โบลาไปประยุกต์ใช้ในชีวิตจริง

   ในอุตสาหกรรมยานยนต์  มีการออกแบบเฟืองท้าย (differential) ซึ่งเป็นอุปกรณ์ที่ทำให้ล้อด้านซ้ายและล้อด้านขวาของรถหมุนไปด้วยความเร็วที่แตกต่างกัน ในขณะเข้าโค้งโดยเฉพาะรถยนต์ที่ขับเคลื่อนล้อหลัง เฟืองท้ายจะมีเฟืองวงแหวน หรือเฟืองบายศรีและเฟืองขับเป็นส่วนประกอบ ซึ่งต้องอาศัยความรู้เกี่ยวกับไฮเพอร์โบลาในการออกแบบการหมุนของเฟืองท้าย และจัดเฟืองขับให้วางเยื้องจากเส้นผ่านศูนย์กลางของเฟืองบายศรี ทำให้เฟืองมีอัตราการขับที่มากกว่า จึงมีเสียงเงียบ เรียกการจัดเฟืองท้ายแบบนี้ว่าไฮปอยด์บีเวล (hypoid bevel gear)

รูปที่ 3 แสดงตำแหน่งการจัดวางของเฟืองขับและเฟืองบายศรีแบบไฮปอยด์บีเวล
ที่มา: http://www.tatc.ac.th/files/09021213134814_11052619190547.pdf

   นอกจากนี้ ในวิชาทัศนศาสตร์ซึ่งเป็นแขนงหนึ่งของ วิชาฟิสิกส์ ที่ศึกษาเกี่ยวกับแสงและการมองเห็นก็มีการใช้สมบัติการสะท้อนของไฮเพอร์โบลาได้อย่างน่าสนใจ โดยแสงที่พุ่งไปที่โฟกัสจุดหนึ่งของกระจกที่มีภาคตัดขวางเป็นไฮเพอร์โบลาหรือที่เรียกว่า กระจกเงาไฮเพอร์โบลา จะกระทบกับกระจกเงาซึ่งทำหน้าที่สะท้อนแสงไปยังโฟกัสอีกจุดหนึ่ง ดังแสดงในรูปที่ 4.1 หลักการดังกล่าวสามารถนำไปใช้สร้างกล้องโทรทรรศน์ได้โดยนำกระจกเงาไฮเพอร์โบลาวางในลำกล้อง เพื่อทำหน้าที่สะท้อนแสงจากกระจกเงาพาราโบลาที่เข้ามาจากภายนอก แสงที่สะท้อนจากกระจกเงาพาราโบลาจะพุ่งไปยังโฟกัสจุดหนึ่ง (F1) ของกระจกเงาไฮเพอร์โบลาและกระจกเงาไฮเพอร์โบลาจะสะท้อนแสงกลับไปยังโฟกัสอีกจุดหนึ่งที่อยู่ในตำแหน่งของนัยน์ตา (F2) ดังแสดงในรูปที่ 4.2

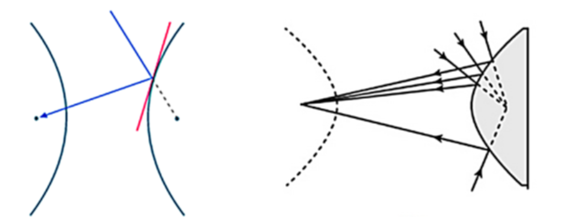
4.1 แสดงสมบัติการสะท้อนของไฮเพอร์โบลา

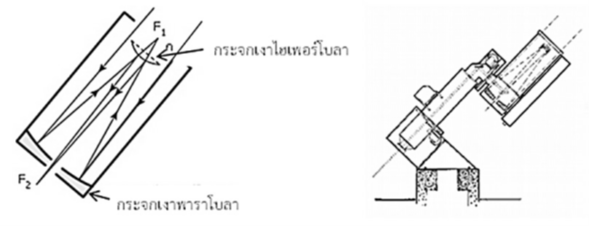
4.2 แสดงหลักการทำงานของกล้องโทรทรรศน์
ที่มา : http://www.myfirstbrain.com/student_view.aspx?ID=88461 และ http://platonicrealms.com/encyclopedia/conics

   คาสสิเกรน (Guillaume Cassegrain) ได้คิดค้นและดัดแปลงกล้องโทรทรรศน์ชนิดสะท้อนแสง โดยอาศัยหลักการเกี่ยวกับพาราโบลาและไฮเพอร์โบลาจนได้กล้องสะท้อนแสงคาสสิเกรน (Cassegrain Reflector) ซึ่งใช้กระจกไพรมารี่ (Primary Mirror) ที่เป็นกระจกเว้าและมีความโค้งเป็นแบบพาราโบลาในการรวบรวมแสงขนานและสะท้อนแสงย้อนไปหน้ากล้อง จากนั้นใช้กระจกชิ้นที่สองซึ่งเป็นกระจกนูนและมีความโค้งไฮเพอร์โบลาทำหน้าที่สะท้อนแสงครั้งที่สอง เพื่อให้ตำแหน่งโฟกัสกลับไปตกที่ท้ายกล้องเรียกโฟกัสแบบนี้ว่า โฟกัสคาสสิเกรน (Cassegrain Focus)

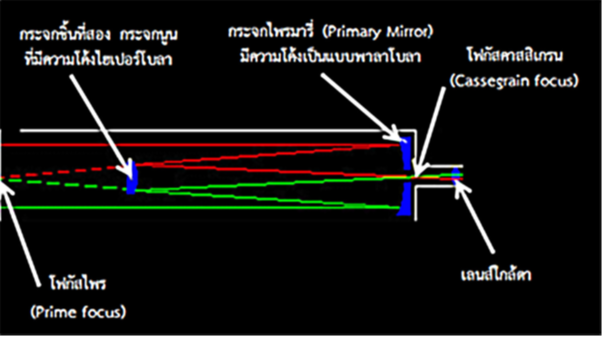
รูปที่ 5 ภาพวาดแสดงทางเดินแสงของกล้องสะท้อนแสงคาสสิเกรน (CassegrainReflector)
ที่มา: http://www.atom.rmutphysics.com/charud/oldnews/0/278/cosmos/35.htm

   ปัจจุบันมนุษย์ได้นำความรู้และหลักการเรื่องไฮเพอร์โบลาเข้ามาประยุกต์ใช้ในการติดตามความเคลื่อนไหว การคมนาคมหรือค้นหาตำแหน่งวัตถุด้วยคลื่นวิทยุ เรียกระบบนี้ว่า LORAN (Long Range Navigation)

   LORAN เป็นระบบค้นหาตำแหน่งของวัตถุ ซึ่งประกอบด้วยสถานีส่งสัญญาณคลื่นวิทยุภาคพื้นดินที่รู้ตำแหน่งแน่นอนอย่างน้อยสองสถานี หนึ่งในนั้นกำหนดให้เป็น MASTER และเรียกสถานีอื่น ๆ ว่า SECONDARY หรือ SLAVE  มีหลักการทำงานคือสถานี MASTER จะส่งคลื่นสัญญาณเป็นวงกลมถึงสถานี SLAVE จากนั้น สถานี SLAVE ก็จะส่งคลื่นสัญญาณเป็นวงกลมความถี่เดิมไปยังตัวรับสัญญาณที่เคลื่อนที่ดังแสดงในรูปที่ 6.1 การมาถึงของ สัญญาณ ณ จุดใด ๆ เช่น จุด P ในรูปที่ 6.1 จะมีเวลาที่ต่างกันขึ้นอยู่กับระยะทาง เวลาในการปล่อยสัญญาณ และตำแหน่งของตัวรับสัญญาณ ซึ่งตัวรับสัญญาณ LORAN จะวัดความแตกต่างของเวลาที่สัญญาณมาถึงจากสถานีต่าง ๆ ซึ่งความแตกต่างจากสถานีคู่ส่งนี้เป็นเส้นโค้งไฮเพอร์โบลา ดังแสดงในรูปที่ 6.2

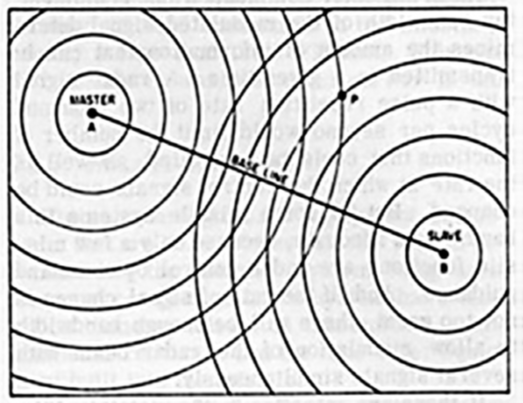
รูปที่ 6.1 แสดงการทำงานของระบบ LORAN  และรูปที่ 6.2 แสดงความแตกต่างค่าคงตัวของเวลาที่มาถึงของสัญญาณ
รูปที่ 6 ระบบ LORAN
ที่มา: http://www.hnsa.org/doc/missile/part2.htm และ http://britton.disted.camosun.bc.ca/jbconics.htm

   ระบบ LORAN นอกจากใช้ในการติดตามความเคลื่อนไหวการคมนาคมทางอากาศ ดังรูปที่ 7.1 แล้วระบบนี้สามารถนำไปใช้กับการคมนาคมทางน้ำได้อีกด้วย เช่น การหาตำแหน่งของเรือเดินสมุทร ดังรูปที่ 7.2 หรือการหาตำแหน่งของวัตถุในระยะไกล

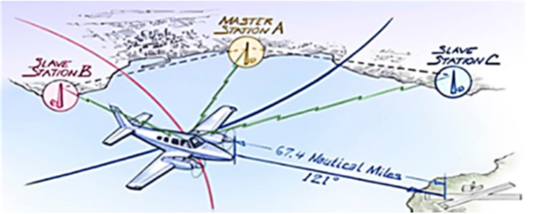
รูปที่ 7.1 แสดงการใช้งานระบบ LORAN สำหรับการคมนาคมทางอากาศ

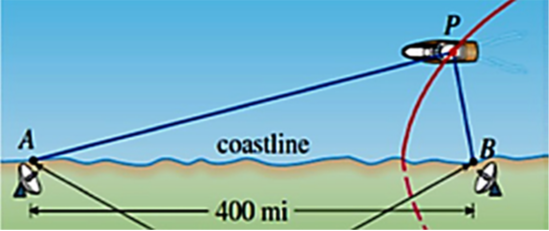
รูปที่ 7.2 แสดงการใช้งานระบบ LORAN สำหรับการคมนาคมทางน้ำ

   นอกจากนี้ มีการนำความรู้เรื่องไฮเพอร์โบลาไปประยุกต์ใช้ในการออกแบบสถาปัตยกรรม เพื่อให้ได้สิ่งก่อสร้างที่มีคุณลักษณะโดดเด่นด้านความงามในเรื่องของรูปทรงหรือองค์ประกอบ เช่น Le planétarium James S. McDonnell เป็นอาคารรวมพิพิธภัณฑ์วิทยาศาสตร์และท้องฟ้าจำลอง ตั้งอยู่ในศูนย์วิทยาศาสตร์เซนต์หลุยส์ (The Saint Louis Science Center) เป็นสถานที่ที่น่าจดจำของนักท่องเที่ยวเป็นอย่างมาก กับโครงสร้างของอาคารแบบ hyperboloid ที่ได้รับการออกแบบโดยสถาปนิก Gyo Obata และสร้างขึ้นในปี ค.ศ. 1963

รูปที่ 8 รูป Le planetarium James S. McDonnell
ที่มา : http://fr.wikipdia.org/wikiPlan%C3%A9tarium_James_S._McDonnell

   ท่าอากาศยานนานาชาติวอชิงตันดัลเลส ในรัฐเวอร์จิเนีย เป็นท่าอากาศยานหลักของยูไนเต็ดแอร์ไลน์  และเป็นศูนย์กลางที่สำคัญสำหรับการเดินทางทางอากาศภายในประเทศและต่างประเทศ มีรูปทรงแบบ hyperboloid ซึ่งได้รับการออกแบบโดย Eero Saarinen

รูปที่ 9 รูป Washington Dulles International Airport
ที่มา: http://www.pleacher.com/mp/mlessons/calculus/apphyper.html

   หอหล่อเย็นของโรงงานผลิตไฟฟ้าพลังงานนิวเคลียร์ที่เยอรมนี เป็นอาคารระบายความร้อนที่ใช้กันทั่วไปในทุกโรงไฟฟ้าพลังงานความร้อน โดยปล่อยไอน้ำจากส่วนของกังหันไอน้ำที่ไม่มีกัมมันตรังสีออกสู่สิ่งแวดล้อมภายนอก ซึ่งมีรูปทรงแบบ hyperboloid ที่ทนต่อแรงลมและใช้วัสดุน้อยชิ้นในการสร้าง

รูปที่ 10 รูปหอหล่อเย็นของโรงงานผลิตไฟฟ้าพลังงานนิวเคลียร์
ที่มา : http://th.wikipedia.org/

   Kobe Port Tower ตั้งอยู่ในสวน Meriken ประเทศญี่ปุ่น เป็นหอชมวิวที่นักท่องเที่ยวสามารถเพลิดเพลินไปกับทัศนียภาพของเมืองโกเบ ซึ่งเป็นอาคารที่สวยงามที่สุดในประเทศญี่ปุ่น และได้รับรางวัลด้านสถาปัตยกรรมหลายรางวัล มีรูปทรงแบบ hyperboloid และสูง 108 เมตร สร้างขึ้นในปี ค.ศ. 1963 โดยมีแรงบันดาลใจจากกลองดั้งเดิมของญี่ปุ่นที่มีรูปร่างเหมือนนาฬิกาทราย

รูปที่ 11 รูป Kobe Port Tower
ที่มา : http://muza-chan.net/japan/index.php/blog/japanese-architecture-kobe-port-towe

   Corporation Street Bridge เป็นสะพานข้ามถนนคอร์ปอเรชัน ใจกลางเมืองแมนเชสเตอร์ซึ่งเชื่อมอาคาร Marks & Spencer / Selfridges กับอาคาร The Manchester Arndale มีรูปทรงแบบ hyperboloid โดยมี Hodder และPartners เป็นสถาปนิกที่ชนะการออกแบบในปี ค.ศ. 1997 ซึ่งการก่อสร้างเกิดขึ้นอย่างรวดเร็วและเสร็จสมบูรณ์พร้อมเปิดใช้งานในปี ค.ศ. 1999

รูปที่ 12 รูป Corporation Street Bridge
ที่มา : http://en.wikipedia.org/wiki/Corporation_Street_Bridge

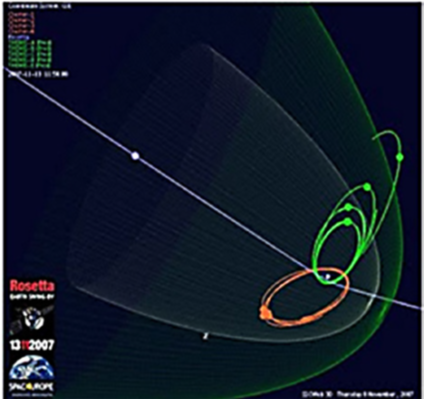
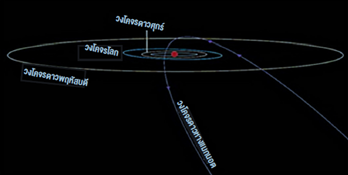
   นอกจากนี้ คนทั่วไปมักเข้าใจว่าวงโคจรของดาวในระบบสุริยะเป็นวงรีเท่านั้น เช่น วงโคจรของดาวเคราะห์รอบดวงอาทิตย์ ดังแสดงในรูปที่ 13.1 วงโคจรของดาวเทียมสำรวจสนามแม่เหล็กโลกดังแสดงในรูปที่ 13.2 แต่ในความเป็นจริง วงโคจรมีหลากหลายรูปแบบ เช่น ดาวหางแบบปรากฏครั้งเดียว (Single-apparition comets) มีการโคจรแบบพาราโบลาหรือไฮเพอร์โบลา หรือดาวหางไม่มีคาบ (Non-periodic comets) จะมีวงโคจรเป็นพาราโบลาหรือไฮเพอร์โบลาในกรณีที่ใช้เวลาโคจรรอบดวงอาทิตย์มากกว่า 200 ปี นอกจากนี้มีดาวหางอีกชนิดหนึ่งที่มีวงโคจรเป็นไฮเพอร์โบลา และโคจรเข้าใกล้โลกมากที่สุด แต่ผ่านมาให้ชาวโลกได้ชมเพียงครั้งเดียวในวันที่ 16 มิถุนายน พ.ศ. 2553 ก่อนจะจากไปตลอดกาลคือดาวหาง C/2009 R1 หรือดาวหางแมคนอต (McNaught) ดังแสดงในรูปที่ 13.3

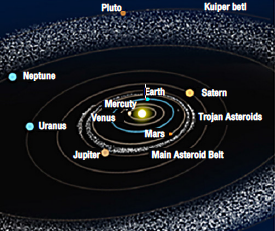
13.1 แสดงวงโคจรของดาวเคราะห์รอบดวงอาทิตย์ที่เป็นวงรี และ 13.2 แสดงวงโคจรของดาวเทียมสำรวจสนามแม่เหล็กโลกที่เป็นวงรี

13.3 แสดงวงโคจรของดาวหาง C/2009 R1 หรือดาวหางแมคนอต (McNaught) ที่เป็นไฮเพอร์โบลา

รูปที่ 13 วงโคจรของดาวในระบบสุริยะ
ที่มา: http://www.lesa.biz/space-technology/satellite/orbits ,http://www.manager.co.th/Science/ViewNewsaspx?NewsID=9530000081180

และ http://www.sunflowercosmos.org/cosmology/cosmology_main/scale_universe%20_1.html

   จะเห็นได้ว่าความรู้เกี่ยวกับไฮเพอร์โบลาและภาคตัดกรวยสามารถนำไปประยุกต์ใช้ในการแก้ปัญหาหรือประดิษฐ์  คิดค้น และสร้างเทคโนโลยีใหม่ ๆ ได้ ดังนั้น ในการจัดกิจกรรมการเรียนรู้ จึงควรเปิดโอกาสให้นักเรียนเรียนรู้จากสิ่งแวดล้อมนอกห้องเรียนด้วย เพื่อให้นักเรียนได้ศึกษาคณิตศาสตร์จากชีวิตจริง ซึ่งจะช่วยให้เกิดความตระหนัก มองเห็นประโยชน์และคุณค่าของการเรียนวิชาคณิตศาสตร์ อย่างแท้จริง อีกทั้งยังช่วยพัฒนาศักยภาพของนักเรียน ในการแก้ปัญหาที่เกิดขึ้นในชีวิตและเตรียมความพร้อมสำหรับการทำงานในอนาคต

บรรณานุกรม

Applications of Hyperbolas. Retrieved June 4, 2014, from http ://www.pleacher.com/mp/mlessons/calculus/apphyper.html

Conic. (2014). Retrieved July 15, 2014, from http ://platonicrealms.com/encyclopedia/conics

Corporation Street Bridge. (2013). Retrieved July 2, 2014, from http ://en.wikipedia.org/wiki/Corporation_Street_Bridge

Japanese Architecture, Kobe Port Tower. (2012). Retrieved, July 2, 2014, from http ://muza-chan.net/japan/index.php/blog/japanese-architecture-kobe-port-tower

The Hyperbola. (2013). Retrieved July 15, 2014, from http ://britton.disted.camosun.bc.ca/jbconics.htm

Le planétarium James S. McDonnell. (2013). Retrieved June 4, 2014, from http ://fr.wikipedia.org/wiki/Plan%C3%A9tarium_James_S._McDonnell

LORAN-C (LOng RAnge Navigation). (2012). Retrieved July 15, 2014, from http ://timeandnavigation.si.edu/multimedia-asset/loran-c-long-range-navigation

LORAN principle. (1997). Retrieved July 15, 2014, from http ://www.hnsa.org/doc/missile/part2.htm

PARABOLA PROBLEMS. Retrieved July 15, 2014, from http ://math-project-athsfuj.weebly.com/part-1-parabola-problems.html

กล้องโทรทรรศน์ . (2554). สืบค้นเมื่อ 18 กรกฎาคม 2557, จาก http ://www.atom.rmutphysics.com/charud/oldnews/0/278/cosmos/35.htm

ขนาดของจักรวาล. (2550). สืบค้นเมื่อ 26 มิถุนายน 2557, จาก http ://www.sunflowercosmos.org/cosmology/cosmology_main/scale_universe%20_1.html

ดาวหางแมคนอต. (2533). สืบค้นเมื่อ 26 มิถุนายน 2557, จาก http ://www.manager.co.th/Science/ViewNews.aspx?NewsID=9530000081180

เฟืองท้ายรถ. สืบค้นเมื่อ 19 กรกฎาคม 2557, จาก http ://www.tatc.ac.th/files/09021213134814_11052619190547.pdf

โรงไฟฟ้านิวเคลียร์ . (2556). สืบค้นเมื่อ 4 มิถุนายน 2557, จาก https://th.wikipedia.org/wiki/โรงไฟฟ้านิวเคลียร์

วงโคจรของดาวเทียม. สืบค้นเมื่อ 26 มิถุนายน 2557, จาก http ://www.lesa.biz/space-technology/satellite/orbits

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2554). หนังสือเรียนรู้รายวิชาเพิ่มเติมคณิตศาสตร์ เล่ม 2 ชั้นมัธยมศึกษาปีที่ 4 - 6 กลมสาระการเรียนรู้คณิตศาสตร์  ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช2551. (พิมพ์ครั้งที่ 3). กรุงเทพมหานคร  : โรงพิมพ์  สกสค. ลาดพร้าว.

ไฮเพอร์โบลา. สืบค้นเมือ 18 กรกฎาคม 2557, จาก http ://www.myfirstbrain.com/student_view.aspx?ID=88461