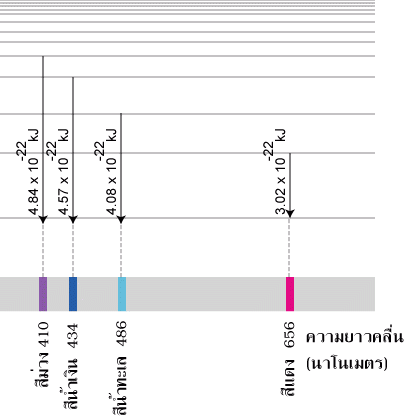เคมีพื้นฐาน
- 1. การแนะนำ
- 2. บทเรียนที่ 2 แบบจำลองอะตอมของดอลตัน
- 3. บทเรียนที่ 3 แบบจำลองอะตอมของทอมสัน
- 4. บทเรียนที่ 4 แบบจำลองอะตอมของรัทเทอร์ฟอร์ด
- 5. บทเรียนที่ 5 อนุภาคในอะตอม
- 6. บทเรียนที่ 6 คลื่นและสมบัติของแสง
- 7. บทเรียนที่ 7 สเปกตรัมเกิดได้อย่างไร
- 8. บทเรียนที่ 8 แบบจำลองอะตอมแบบกลุ่มหมอก
- 9. บทเรียนที่ 9 การจัดเรียงอิเล้กตรอนในอะตอม
- 10. บทเรียนที่ 10 การจัดเรียงอิเล็กตรอนในอะตอม(ต่อ)
- 11. บทเรียนที่ 10 วิวัฒนาการของการสร้างตารางธาตุ
- 12. บทเรียนที่ 11 วิวัฒนการของการสร้างตารางธาตุ
- 13. บทเรียนที่ 12 ขนาดอะตอม
- 14. แบบฝึกหัดที่ 13 พลังงานไอออไนเซชัน
- 15. บทเรียนที่ 14 อิเล็กโทรเนกาติวิตี
- 16. บทเรียนที่ 15 สัมพรรคภาพอิเล็กตรอน
- 17. บทเรียนที่ 16 จุดหลอมเหลว-จุดเดือด
- 18. บทเรียนที่ 17 เลขออกซิเดชัน
- - ทุกหน้า -
![]()
บทเรียนที่ 1 การวัด
หน่วยที่ 1
Introduction to Instrumentation
เครื่องมือวัดทางอิเล็กทรอนิกส์นั้นมีหลายลักษณะและรูปแบบ ถ้าอยู่ในห้องทดลองก็จะเป็นชนิดเครื่องมือวัดและทดสอบ เพื่อใช้สำหรับวิเคราะห์วงจรทางอิเล็กทรอนิกส์ต่าง ๆ กระแส แรงเคลื่อน กำลังงาน ความต้านทาน ฯลฯ เครื่องมือวัดทางอิเล็กทรอนิกส์ที่แสดงให้เราทราบค่านั้น จะเป็น 2 ลักษณะ คือ
1. ลักษณะที่แสดงให้ทราบค่าโดยใช้เข็มชี้ ซึ่งจะหมุนขึ้นลงบนหน้าปัทม์ ตามความแรงของกระแสที่ไหลผ่านขดลวดมูฟวิ่งคอยล์ ( Moving Coil )ค่าของหน่วยไฟฟ้าต่างๆบนสเกลที่จะแสดงไว้จะปรับค่ามาตรฐานซึ่งเครื่องมือวัดชนิดนี้ เรียกว่า แบบอนาล็อก ( Analog Instrument )
2. ลักษณะที่แสดงให้ทราบค่าโดยแสดงเป็นตัวเลข ค่าของหน่วยไฟฟ้าต่างๆที่จะแสดงไว้จะปรับค่ามาตรฐานซึ่งเครื่องมือวัดชนิดนี้ เรียกว่า แบบดิจิตอล ( Digital Instrument )
เครื่องมือวัดหลายชนิดจะทำหน้าที่ให้ข้อมูลเชิงปริมาณของตัวแปรต่าง ๆ และในบางครั้งยังทำหน้าที่บันทึกข้อมูลไว้ด้วย นอกจากนี้เครื่องมือวัดบางชนิดยังทำหน้าที่ควบคุมจำนวนต่าง ๆด้วย จึงสรุปได้ว่า เครื่องมือวัดจะทำหน้าที่อยู่ 3 อย่างคือ แสดงค่า( Indicating ) , บันทึก (Recording) , และ ควบคุม ( Controlling ) ซึ่งเครื่องมือวัดบางชนิดอาจจะทำหน้าที่เพียงอย่างเดียว หรือพร้อมกันก็ได้ จุดประสงค์ทั่วไปของเครื่องมือวัดทางไฟฟ้าและอิเล็กทรอนิกส์จะทำหน้าที่เพียงสองอย่างคือ แสดงค่าและบันทึกค่า
สำหรับการวัดกระแส แรงดันทางไฟฟ้า จะมีเครื่องมือวัดทางอิเล็กทรอนิกส์ที่มีราคาแพงกว่าเครื่องมือวัดทางไฟฟ้าทั่วไป ที่เป็นเช่นนี้ก็เพื่อสนองความต้องการหลายอย่าง เช่น การใช้วงจรขยายอิเล็กทรอนิกส์ เป็นผลทำให้เครื่องวัดมีความไวสูง ( High Sensitivity ) สามารถทำการวัดสัญญาณที่มีขนาดเล็กมากได้ ( Low Amplitude Signal ) การที่มีความไวสูงนี้สามารถเพิ่มอินพุตอิมพีแดนซ์ ( Input Impedance ) ให้แก่เครื่องวัด และเป็นผลทำให้ลดผลของการโหลดในวงจรเมื่อทำการวัด
1.1 หน่วยวัดทางไฟฟ้า
เนื่องจากเครื่องวัดทางไฟฟ้าและทางอิเล็กทรอนิกส์ วัดปริมาณทางไฟฟ้า ดังนั้นจึงจำเป็นต้องเรียนรู้หน่วยทางไฟฟ้า รวมทั้งหน่วยทางวิทยาศาสตร์อื่น ๆ ที่เกี่ยวข้อง
ปริมาณทางไฟฟ้ามีอยู่ 6 ชนิด ที่เกี่ยวข้องกับการวัด คือ
1. ประจุไฟฟ้า ( Electrical Charge ) ใช้สัญลักษณ์ Q
2. กระแสไฟฟ้า ( Electrical Current ) ใช้สัญลักษณ์ I
3. แรงเคลื่อนไฟฟ้าหรือความต่างศักย์ ใช้สัญลักษณ์ V
( Electromotive Force or Potential Difference)
4. ความต้านทาน ( Resistance ) ใช้สัญลักษณ์ R
5. ตัวนำ ( Inductance ) ใช้สัญลักษณ์ L
6. ความจุ ( Capacitance ) ใช้สัญลักษณ์ C
|
ปริมาณ ( Quantity ) |
สัญลักษณ์ ( Symbol ) |
หน่วย ( Unit ) |
อักษรย่อของหน่วย ( Unit Abbreviation ) |
|
หน่วยพื้นฐาน ยาว / กว้าง / สูง ( Length ) น้ำหนัก ( Mass ) เวลา ( Time ) อุณหภูมิทางเทอร์โมไดนามิกส์ ( Temperature ) ความเข้มของการส่องสว่าง ( Luminous Intensity ) |
l m t T |
เมตร กิโลกรัม วินาที องศาเคลวิน (Kelvin ) แคนเดอล่า ( Candela ) |
m. kg. s. k. cd. |
|
หน่วยทางไฟฟ้า กระแสไฟฟ้า ( Electrical Current ) แรงเคลื่อนไฟฟ้า ( Electromotive Force) ปริมาณการประจุ ( Quantity of Charge) ความต้านทานทางไฟฟ้า (Electrical Resistance ) ความจุ ( Capacitance ) ความนำ ( Inductance ) |
I V Q R C L |
แอมแปร์ โวลท์ (Volt) คูลอมป์ โอหม์ ( Ohm ) ฟารัด(Farad) เฮนรี่ (Henry) |
A. V. C. W F. H. |
ตารางที่ 1.1 แสดงปริมาณสัญลักษณ์และอักษรย่อของระบบ SI ( System International unit )
1.2 มาตรฐานการวัด
มาตรฐานการวัด ( Standard of measurement ) แบ่งได้ 4 ประเภท คือ
- มาตรฐานสากล ( International standard )
- มาตรฐานหลักขั้นต้น ( Primary standard )
- มาตรฐานหลักขั้นรอง ( Secondary standard )
- มาตรฐานใช้งาน ( Working standard )
1.2.1 มาตรฐานสากล คือข้อตกลงระดับชาติที่ได้กำหนดและวางรากฐานของหน่วย ( Units ของการวัดให้มีความเที่ยงตรงหรือใกล้เคียงที่สุดของผลิตภัณฑ์ และเทคโนโลยีในการผลิตและการวัดจะเอื้ออำนวยให้ มาตรฐานสากลจะถูกตรวจและทดสอบค่าอย่างสม่ำเสมอ โดยการวัดแบบสัมบูรณ์ ในรูปของหน่วยพื้นฐาน ( ความยาว มวล เวลา กระแส อุณหภูมิ ความเข้มของการส่องสว่าง ) มาตรฐานเหล่านี้จะถูกเก็บรักษาอยู่ที่ International Bureau of Weights and Measures ( BIPM ) และไม่ได้ใช้ในการเปรียบเทียบ ( Comparison ) หรือปรับเทียบ ( Calibration )
1.2.2 มาตรฐานขั้นต้น เป็นประเภทที่รองลงมาจากมาตรฐานสากล จะถูกเก็บรักษาให้คงมาตรฐาน ที่ห้องปฏิบัติการมาตรฐานแห่งชาติ ในส่วนต่าง ๆ ของโลก เช่น National Bureau of standard ( NBS ปัจจุบันเป็น NIST ) ในวอชิงตัน จะเก็บมาตรฐานขั้นต้นสำหรับทวีปอเมริกาเหนือ เช่นเดียวกับประเทศอังกฤษก็มีห้องปฏิบัติการมาตรฐานแห่งชาติ คือ National Physics Laboratory ( NPL ) และประเทศเยอรมัน
ก็มีห้องปฏิบัติการมาตรฐานแห่งชาติ คือ Physikalisch Technische Reiehsanstalt มาตรฐานขั้นต้นจะใช้แต่เพียงในห้องปฏิบัติการแห่งชาติเท่านั้น โดยใช้ตรวจสอบเพื่อยืนยันความถูกต้อง และปรับเทียบมาตรฐานขั้นรอง
1.2.3 มาตรฐานขั้นรอง มาตรฐานนี้จะถูกยึดปฏิบัติในกลุ่มของอุหสาหกรรมที่เกี่ยวข้องโดยเฉพาะอย่าง และจะนำมาเปรียบเทียบกันเองในกลุ่ม และจะทดสอบกันเป็นระยะ ๆ กับมาตรฐานขั้นต้น โดยส่งให้ห้องทดสอบระดับชาติเป็นผู้ทดสอบและปรับแต่ง ( Calibrate ) แล้วส่งกลับมายังกลุ่ม โรงงานอุตสาหกรรมนั้น พร้อมกับออกใบรับรองค่าผิดพลาด โดยยึดหรือเทียบกับมาตรฐานขั้นต้น
1.2.4 มาตรฐานใช้งาน จะเป็นมาตรฐานที่สำคัญยิ่งในขั้นปฏิบัติงาน โดยจะเป็นการนำเครื่องมือ เครื่องวัดต่าง ๆ ในโรงงานมาปรับปรุงแก้ไข ให้ได้ความเที่ยงตรงให้อยู่ในมาตรฐานที่กำหนด
1.1มาตรฐานสากลของหน่วยทางไฟฟ้า
1.3.1 กระแสมาตรฐาน ( Current standard )
ในระบบ SI ให้คำจำกัดความของหน่วยแอมแปร์ ซึ่งเป็นหน่วยของกระแสไฟฟ้า ว่าได้จากการนำลวดทองแดงมาวางขนานกันสองเส้น ห่างกัน 1 เมตร ในหลอดแก้วสูญญากาศ โดยความยาวภายนอกหลอดแก้วยาวมากแบบอนันต์ โดยค่ากระแสของหนึ่งแอมแปร์จะทำให้เกิดแรงดึงดูดของเส้นลวดทั้งสองเส้นเป็น 2 X 10-7นิวตันต่อเมตร การวัดครั้งแรกมีการผิดพลาดมาก แต่ต่อมา แอมแปร์สากลได้ใช้หลักการดึงดูดของสายทองแดงเดิมขนาดมาตรฐานสองเส้นวางห่างกันหนึ่งเมตร โดยกระบวนการและเทคโนโลยีสมัยใหม่ขึ้นและจัดสมดุลและแก้ไขทางกระแสและแรงดัน จึงทำให้ได้มาตรฐานของแอมแปร์ซึ่งภายหลังเป็นที่ยอมรับเป็นมาตรฐานสากล
1.3.2 ความต้านทานมาตรฐาน ( Resistance standard )
ค่ามาตรฐานของความต้านทานซึ่งมีหน่วยเป็นโอห์ม ได้ถูกสร้างขึ้นมาโดยสมาคมมาตรฐานสากล BIPM และสมาคม NBS โดยจะทำการทดสอบเป็นระยะ ๆ โดยกำหนดได้ว่า ค่าความต้านทาน หนึ่งโอห์ม จะได้จากความต้านทานของขดลวดแมงกานิน ( Manganin ) (โลหะผสมที่ประกอบด้วยทองแดง 85 % แมงกานีส 11 % และนิเกิล 4 % ) ซึ่งมีความต้านทานคงตัวและไม่แปรเปลี่ยนต่ออุณหภูมิ
ประเทศรับรอง
1.3.3 มาตรฐานทางโวลท์ ( Voltage standard )
สมาคม NBS ได้มาตรฐานของโวลท์ซึ่งจะใช้เซลล์แบตตอรี่ของเวสตัน ( Weston Cell ) ลักษณะของเวสตันเซลล์จะประกอบขึ้นดังรูปที่ 1.2 โดยมีขั้วบวกเป็นปรอท และขั้วลบเป็นเซลล์แคดเมียมอะมาลกัม ( cadmiun amalgam ) มีจำนวนแคดเมียมร้อยละ 10 สารละลายทางไฟฟ้า หรือที่เรียกว่าอิเล็กโทรไลต์ ( Electrolyte ) เป็นสารละลายของแคดเมียมซัลเฟต ( cadmiun sulphate ) โดยทั้งหมดอยู่ในหลอดแก้วรูปตัวเฮส ( H )
1.2 ข้อผิดพลาดในการวัด
การวัดเป็นขบวนการเปรียบเทียบ ระหว่างปริมาณที่ไม่ทราบค่า กับปริมาณมาตรฐาน จะเกี่ยวข้องกับการต่อเครื่องมือวัดเข้ากับระบบที่ต้องการจะวัด ดังนั้นการวัดนี้จึงเป็นการแสดงค่าวัดที่ออกมาโดยมีชื่อเรียกว่า ค่าที่วัดได้ แต่เนื่องจากว่าการวัดใด ๆ จะมีผลกระทบต่อตัวแปรหลายตัว ดังนั้นค่าที่วัดได้จึงไม่ใช่เป็นค่า ค่าจริง ( True Value ) ปัจจัยบางประการที่มีผลกระทบต่อการวัดเกิดจากเครื่องมือวัดเอง และบุคคลที่ใช้เครื่องมือวัดอันนั้น การเบี่ยงเบนค่าที่วัดได้ที่แตกต่างไปจากค่าจริง คือ ข้อผิดพลาด ( Error ) ของการวัด ข้อผิดพลาดอาจจะเป็นแอ็บโซลูต ( Absolute ) หรือสิ่งที่วัด กับ ค่าที่วัดได้จริงจากสิ่งนั้น
1.4.1 ค่าผิดพลาดเป็นแอ็บโซลูต ( Absolute ) หมายถึงผลต่างของค่าที่วัดได้กับค่าจริง เขียนเป็นสมการดังนี้
E = Yn - Xn
เมื่อ
E = ค่าแอ็บโซลูต
Yn = ค่าจริง
Xn = ค่าที่วัดได้
ถ้าเราต้องการแสดงค่าที่ผิดพลาดเป็นเปอร์เซ็นต์ อาจเขียนเป็นสมการได้ดังนี้
เปอร์เซ็นต์ที่ผิดพลาด = ค่าผิดพลาดแอ็บโซลูต X 100
ค่าจริง
หรือ
เปอร์เซ็นต์ที่ผิดพลาด =
แทนค่า E ในสมการ
เปอร์เซ็นต์ที่ผิดพลาด = X 100
1.4.2 ค่าความถูกต้อง ( Accuracy ) หมายถึง ความใกล้เคียงระหว่างค่าที่เป็นจริงกับค่าที่อ่านได้จากเครื่องวัด เขียนเป็นสมการดังนี้
A = 1 -
และ เปอร์เซ็นต์ความถูกต้อง = A X 100 %
ตัวอย่างที่1.1
ค่าโวลท์เตจตกคร่อมความต้านทานตัวหนึ่ง ซึ่งคำนวณได้คือ 100 V แต่วัดได้จริง 98 V ให้หาค่าต่าง ๆ ดังนี้
(ก) ค่าผิดพลาดแอ็บโซลูต (ค) ค่าความเที่ยงตรง
(ข) เปอร์เซ็นต์ของการผิดพลาด (ง) เปอร์เซ็นต์ของความถูกต้อง
(ก) E = Yn - Xn
= 100 V - 98 V = 2 V
(ข) เปอร์เซ็นต์ผิดพลาด = X 100
= X 100 = 2 %
(ค) ค่าความเที่ยงตรง (A) = 1 - X 100 %
= 1 - 0.02 = 0.98
(ง) เปอร์เซ็นต์ของความถูกต้อง = 100 % X 0.98
= 98 %
1.1 ชนิดของความผิดพลาด
ความผิดพลาดจะปรากฏเสมอในทุกการวัด เนื่องจากเราไม่สามารถทำการวัดโดยไม่มีความผิดพลาดได้ ซึ่งข้อผิดพลาดดังกล่าวอาจจะแบ่งออกได้เป็น 3 ลักษณะด้วยกันคือ
1.5.1. ความผิดพลาดเนื่องจากผู้ทำการวัด ( Gross Error ) หมายถึงข้อผิดพลาดที่เกิดขึ้นจากความบกพร่องของบุคคลที่ใช้เครื่องมือวัด เช่น การอ่านค่าเครื่องมือวัดผิด หรือการใช้เครื่องวัดไม่ถูกต้อง
1.5.2. ความผิดพลาดจากระบบ ( Systematic Error ) หมายถึงข้อผิดพลาดที่เกิดจากตัวเครื่องมือวัดเอง ซึ่งสามารถแบ่งย่อยได้เป็น
1. ความผิดพลาดเนื่องจากเครื่องวัด ( Instrumental Error ) ข้อผิดพลาดนี้อาจเกิดจากความยืดของแบร์ริ่งของส่วนเคลื่อนไหวของมิเตอร์ ( Meter Movement ) แรงดึงของสปริงไม่ถูกต้อง การปรับแต่งไม่ถูกต้อง หรือตัวเครื่องมือบกพร่องเอง ข้อผิดพลาดนี้สามารถลดลงได้โดยการบำรุงรักษาที่ถูกต้อง การใช้และการรักษา
2. ความผิดพลาดเนื่องจากสิ่งแวดล้อม ( Environmental Error ) ข้อผิดพลาดนี้เกิดจากสภาพแวดล้อมในสถานที่ใช้เครื่องมือวัดชนิดนั้น เช่น มีอุณหภูมิสูง ความกดดันอากาศสูง ความชื้น หรือมีสนามไฟฟ้าสถิต หรือสนามแม่เหล็กเป็นผลกระทบต่อเครื่องวัด
1.5.3. ความผิดพลาดแบบแรนดอม ( Random Error ) ข้อผิดพลาดนี้เกิดขึ้นหลังจากการ แก้ไขของข้อผิดพลาดจากผู้ใช้ และข้อผิดพลาดจากระบบแล้ว ซึ่งจะมีค่าน้อยลงแล้ว หรืออาจจะเกิดจากการสะสมจำนวนมาก ซึ่งจะมีผลกระทบน้อยที่จะทราบค่าได้จากการวิเคราะห์เชิงสถิติเท่านั้น ซึ่งเราอาจจะยอมรับได้เพราะมีค่าน้อยมาก
1.2 การจำกัดข้อผิดพลาด
บริษัทผู้ผลิตเครื่องมือวัดเกือบทั้งหมดจะกำหนดความถูกต้อง (Accuracy) ของเครื่องวัดภายใต้เปอร์เซ็นต์ที่กำหนดได้จากการอ่านค่าเต็มเสกล เช่น บริษัทผู้ผลิตโวลท์มิเตอร์แห่งหนึ่งจะกำหนดไว้ว่าเครื่องมือวัดจะถูกต้องภายใน + 2 % ของการที่เข็มชี้เต็มสเกล ( Accuracy + 2 % of full scale ) รายละเอียดเฉพาะนี้เรียกว่า การจำกัดข้อผิดพลาด ซึ่งหมายความว่าบริษัทจะประกันว่าเมื่อเข็มชี้เต็มสเกลนั้น จะมีข้อผิดพลาดไม่เกิน + 2 % ดังนั้น ถ้าเข็มชี้น้อยกว่าเต็มสเกลแล้วข้อผิดพลาดก็จะลดน้อยลงตามลำดับ เช่น โวลท์มิเตอร์ชนิด 300 V กำหนดไว้ว่า Accuracy + 2 % of full scale จะคำนวณหาค่าความจำกัดข้อผิดพลาดของเครื่องมือวัดนี้ เมื่อใช้วัดโวลท์เตจที่ 120 V
แทนค่าในสมการได้ดังนี้
ขนาดของความจำกัดข้อผิดพลาดคือ 0.02 X 300 V = 6 V ( ที่เต็มสเกล )
เพราะฉะนั้น ค่าความจำกัดข้อผิดพลาดที่ 120 V คือ X 100 = 5 %
ตัวอย่างที่1.3
Voltmeter และ Ammeter ตัวหนึ่งใช้วัดกำลังที่สูญเสียไปในความต้านทานตัวหนึ่ง เครื่องวัดทั้งสองรับประกันความผิดพลาดภายใน + 1 % ของการวัดเต็มสเกล ( Accuracy + 1 % of full scale ) ถ้า Voltmeter อ่านค่าได้ 80 V บนสเกล 150 V และ Ammeter อ่านค่าได้ 70 mA บนสเกล 100 mA ให้คำนวณหาค่าความผิดพลาดจากการวัดกำลังที่สูญเสียไป จากความต้านทานตัวนี้
แทนค่าในสมการ
ขนาดของความผิดพลาดสำหรับ Voltmeter คือ
0.01 X 150 V = 1.5 V.
ข้อจำกัดของความผิดพลาดที่ 80 V คือ
X 100 % = 1.87 %
ขนาดของความผิดพลาดสำหรับ Ammeter คือ
0.01 X 100 mA = 1 mA.
ข้อจำกัดของความผิดพลาดที่ 100 mA คือ
X 100 % = 1.43 %
เพราะฉะนั้นข้อผิดพลาดสำหรับการหาค่ารวมของกำลังงานที่ถูกใช้ไปแต่ละตัว คือ
ข้อผิดพลาดรวม = 1.87 % + 1.43 %
= 3.30 %
กลับไปที่เนื้อหา
บทเรียนที่ 2 แบบจำลองอะตอมของดอลตัน
อะตอม เป็นคำที่มาจากภาษากรีกว่าatomosโดยนักปราชญ์กรีกยุคโบราณมีความเชื่อว่า สิ่งของต่าง ๆ ประกอบด้วยอนุภาคขนาดเล็กมาก เมื่อแบ่งสารต่าง ๆ ออกไปเรื่อย ๆ จนมีขนาดเล็กที่สุดซึ่งไม่สามารถแบ่งได้อีกต่อไป จึงเรียกอนุภาคที่เล็กที่สุดนี้ว่า“อะตอม”
แบบจำลองอะตอม:
เป็นที่ยอมรับกันแล้วว่าสารต่าง ๆ นั้นประกอบด้วยอะตอม แต่อย่างไรก็ตามยังไม่มีผู้ใดเคยเห็นรูปร่างที่แท้จริงของอะตอม รูปร่างหรือโครงสร้างของอะตอมจึงเป็นเพียงจินตนาการหรือมโนภาพที่สร้างขึ้นเพื่อให้สอดคล้องกับการทดลอง เรียกว่า“แบบจำลอง”ซึ่งจัดเป็นทฤษฎีประเภทหนึ่ง แบบจำลองอะตอมอาจเปลี่ยนแปลงไปได้ตามผลการทดลองหรือข้อมูลใหม่ ๆ เมื่อแบบจำลองอะตอมเดิมอธิบายไม่ได้ ดังนั้นแบบจำลองอะตอมจึงได้มีการแก้ไขพัฒนาหลายครั้งเพื่อให้สอดคล้องกับการทดลอง นักวิทยาศาสตร์ได้ใช้กล้องจุลทรรศน์อิเล็กตรอนที่มีกำลังขยายสูงมากร่วมกับคอมพิวเตอร์ และถ่ายภาพที่เชื่อว่าเป็นภาพภายนอกของอะตอม
วิวัฒนาการของแบบจำลองอะตอม
วิวัฒนาการของแบบจำลองอะตอมตั้งแต่อดีตจนถึงปัจจุบันมีดังนี้
- แบบจำลองอะตอมของดอลตัน
- แบบจำลองอะตอมของทอมสัน
- แบบจำลองอะตอมของรัทเทอร์ฟอรด์
- แบบจำลองอะตอมของโบร์
- แบบจำลองอะตอมแบบกลุ่มหมอก
กลับไปที่เนื้อหา
บทเรียนที่ 3 แบบจำลองอะตอมของทอมสัน
การนำไฟฟ้าของแก๊ส
ปกติแก๊สเป็นตัวนำไฟฟ้าที่ไม่ดี ปรากฏการณ์ที่ยืนยันได้ว่าแก๊สนำไฟฟ้าได้ก็คือการเกิดฟ้าแลบ ฟ้าผ่า แก๊สนำไฟฟ้าได้ดีขึ้นเมื่อแก๊สมีความดันต่ำ ๆ และมีความต่างศักย์ของขั้วไฟฟ้าสูง ๆ แก๊สนำไฟฟ้าได้เพราะแก๊สสามารถแตกตัวเป็นไอออนบวกและอิเล็กตรอน เมื่ออยู่ในสนามไฟฟ้าศักย์สูง ๆ เช่น แก๊สฮีเลียม (He) และแก๊สไฮโดรเจน (H2) จะเกิดการแตกตัวดังสมการ
He(g) ---------- > He+(g) + e–
H(g) ----------- > H+(g) + e–
รางวัลโนเบล (Nobel Prize) สาขาฟิสิกส์ ในปีค.ศ. 1906
United Kingdom
University of Cambridge
Cambridge, United Kingdom
มีชีวิตอยู่ระหว่างปี 1856 - 1940
เซอร์ โจเซฟ จอห์น ทอมสัน (J.J Thomson) นักวิทยาศาสตร์ชาวอังกฤษได้สนใจปรากฏการณ์ที่เกิดขึ้นในหลอดรังสีแคโทด จึงทำการทดลองเกียวกับการนำไฟฟ้าของแก๊สขึ้นในปี พ.ศ. 2440 (ค.ศ. 1897) และได้สรุปสมบัติของรังสีไว้หลายประการ ดังนี้
1. รังสีแคโทดเดินทางเป็นเส้นตรงจากขั้วแคโทดไปยังขั้วแอโนด เนื่องจากรังสีแคโทดทำให้เกิดเงาดำของวัตถุได้ ถ้านำวัตถุไปขวางทางเดินของรังสี
2.รังสีแคโทดเป็นอนุภาคที่มีมวล เนื่องจากรังสีทำให้ใบพัดที่ขวางทางเดินของรังสีหมุนได้เหมือนถูกลมพัด
3. รังสีแคโทดประกอบด้วยอนุภาคที่มีประจุลบ เนื่องจากเบี่ยงเบนเข้าหาขั้วบวกของสนามไฟฟ้า
จากผลการทดลองนี้ ทอมสันอธิบายได้ว่า อะตอมของโลหะที่ขั้วแคโทดเมื่อได้รับกระแสไฟฟ้าที่มีความต่างศักย์สูงจะปล่อยอิเล็กตรอนออกมาจากอะตอม อิเล็กตรอนมีพลังงานสูง และเคลื่อนที่ภายในหลอด ถ้าเคลื่อนที่ชนอะตอมของแก๊สจะทำให้อิเล็กตรอนในอะตอมของแก๊สหลุดออกจากอะตอม อิเล็กตรอนจากขั้วแคโทดและจากแก๊สซึ่งเป็นประจุลบจะเคลื่อนที่ไปยังขั้วแอโนด ขณะเคลื่อนที่ถ้ากระทบฉากที่ฉาบสารเรืองแสง เช่นZnSทำให้ฉากเกิดการเรืองแสง ซึ่งทอมสันสรุปว่ารังสีแคโทดประกอบด้วยอนุภาคที่มีประจุลบเรียกว่า“อิเล็กตรอน”และยังได้หาค่าอัตราส่วนประจุต่อมวล (e/m) ของอิเล็กตรอนโดยใช้สยามแม่เหล็กและสนามไฟฟ้าช่วยในการหา ซึ่งได้ค่าประจุต่อมวลของอิเล็กตรอนเท่ากับ 1.76x 108C/gค่าอัตราส่วนe/mนี้จะมีค่าคงที่ ไม่ขึ้นอยู่กับชนิดของโลหะที่เป็นขั้วแคโทด และไม่ขึ้นอยู่กับชนิดของแก๊สที่บรรจุอยู่ในหลอดรังสีแคโทด แสดงว่าในรังสีแคโทดประกอบด้วยอนุภาคไฟฟ้าที่มีประจุลบเหมือนกันหมดคืออิเล็กตรอนนั่นเอง ทอมสันจึงสรุปว่า
| “อิเล็กตรอนเป็นส่วนประกอบส่วนหนึ่งของอะตอม และอิเล็กตรอนของทุกอะตอมจะมีสมบัติเหมือนกัน” |

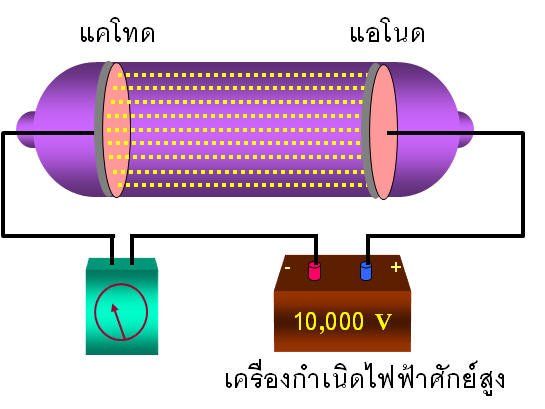
ปรากฏการณ์ที่เกิดขึ้นในหลอดรังสีแคโทด
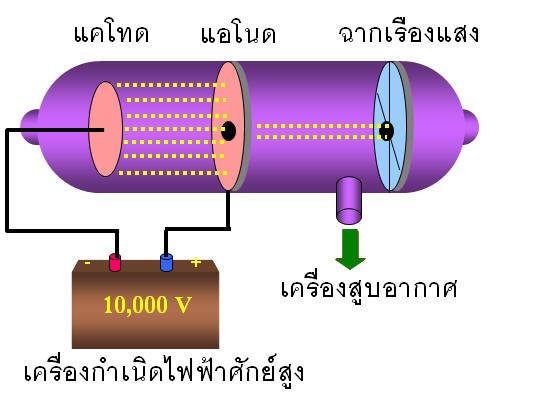
รังสีแคโทดเดินทางเป็นเส้นตรงจากขั้วแคโทดไปยังขั้วแอโนด
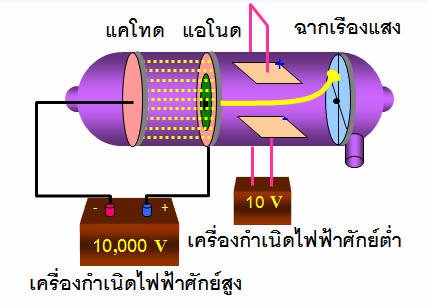
รังสีแคโทดบี่ยงเบนเข้าหาขั้วบวกของสนามไฟฟ้า
การค้นพบโปรตอน
ในปี พ.ศ. 2409 (ค.ศ. 1866) ออยเกน โกลด์ชไตน์ นักวิทยาศาสตร์ชาวเยอรมัน ได้ทำการทดลองโดยเจาะรูที่ขั้วแคโทดในหลอดรังสีแคโทด พบว่าเมื่อผ่านกระแสไฟฟ้าเข้าไปในหลอดรังสีแคโทดจะมีอนุภาคชนิดหนึ่งเคลื่อนที่เป็นเส้นตรงไปในทิศทางตรงกันข้ามกับการเคลื่อนที่ของรังสีแคโทดผ่านรูของขั้วแคโทด และทำให้ฉากด้านหลังขั้วแคโทดเรืองแสงได้ โกลด์ชไตน์ได้ตั้งชื่อว่า“รังสีแคแนล”(canal ray)หรือ“รังสีบวก”(positive ray)สมบัติของรังสีบวกมีดังนี้
1. เดินทางเป็นเส้นตรงไปยังขั้วแคโทด
2. เมื่อผ่านรังสีนี้ไปยังสนามแม่เหล็กและสนามไฟฟ้า รังสีนี้จะเบี่ยงเบนไปในทิศทางตรงข้ามกับรังสีแคโทด แสดงว่ารังสีนี้ประกอบด้วยอนุภาคที่มีประจุไฟฟ้าเป็นบวก
3. มีอัตราส่วนประจุต่อมวลไม่คงที่ ขึ้นอยู่กับชนิดของแก๊สในหลอด และถ้าเป็นแก๊สไฮโดรเจนรังสีนี้จะมีอัตราส่วนประจุต่อมวลสูงสุด เรียกอนุภาคบวกในรังสีแคแนลของไฮโดรเจนว่า“โปรตอน”
4.มีมวลมากกว่ารังสีแคโทด เนื่องจากความเร็วในการเคลื่อนที่ต่ำกว่ารังสีแคโทด
ทอมสันได้วิเคราะห์การทดลองของโกลด์ ชไตน์ และการทดลองของทอมสัน จึงเสนอแบบจำลองอะตอมว่า
|
“อะตอมเป็นรูปทรงกลมประกอบด้วยเนื้ออะตอมซึ่งมีประจุบวกและมีอิเล็กตรอนซึ่งมีประจุลบกระจายอยู่ทั่วไป อะตอมในสภาพที่เป็นกลางทางไฟฟ้าจะมีจำนวนประจุบวกเท่ากับจำนวนประจุลบ” |
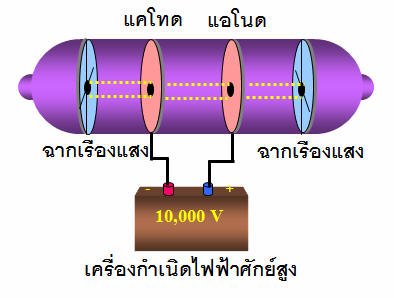

แบบจำลองอะตอมของทอมสัน
กลับไปที่เนื้อหา
บทเรียนที่ 4 แบบจำลองอะตอมของรัทเทอร์ฟอร์ด
แบบจำลองอะตอมของรัทเทอร์ฟอร์ด
ในปี พ.ศ. 2453 (ค.ศ. 1910) เซอร์ เออร์เนสต์ รัทเทอร์ฟอร์ด (Sir Ernest Rutherford) ได้ศึกษาแบบจำลองอะตอมของทอมสัน และเกิดความสงสัยว่าอะตอมจะมีโครงสร้างตามแบบจำลองของทอมสันจริงหรือไม่ โดยตั้งสมมติฐานว่า
“ถ้าอะตอมมีโครงสร้างตามแบบจำลองของทอมสันจริง ดังนั้นเมื่อยิงอนุภาคแอลฟาซึ่งมีประจุไฟฟ้าเป็นบวกเข้าไปในอะตอม แอลฟาทุกอนุภาคจะทะลุผ่านเป็นเส้นตรงทั้งหมดเนื่องจากอะตอมมีความหนาแน่นสม่ำเสมอเหมือนกันหมดทั้งอะตอม”
เพื่อพิสูจน์สมมติฐานนี้ รัทเทอร์ฟอร์ดได้ทำการทดลองยิงอนุภาคแอลฟาไปยังแผ่นทองคำบาง ๆ โดยมีความหนาไม่เกิน 10–4 cm โดยมีฉากสารเรืองแสงรองรับ ปรากฏผลการทดลองดังนี้
1. อนุภาคส่วนมากเคลื่อนที่ทะลุผ่านแผ่นทองคำเป็นเส้นตรง
2. อนุภาคส่วนน้อยเบี่ยงเบนไปจากเส้นตรง
3. อนุภาคส่วนน้อยมากสะท้อนกลับมาด้านหน้าของแผ่นทองคำ
Ernest_Rutherford
รางวัลโนเบลสาขาเคมี ปี ค.ศ.1908
United Kingdom and New Zealand
Victoria University
Manchester, United Kingdom
มีชีวิตอยู่ระหว่าง ค.ศ. 1871 -1937
ถ้าแบบจำลองอะตอมของทอมสันถูกต้อง เมื่อยิงอนุภาคแอลฟาไปยังแผ่นทองคำบาง ๆ นี้ อนุภาคแอลฟาควรพุ่งทะลุผ่านเป็นเส้นตรงทั้งหมดหรือเบี่ยงเบนเพียงเล็กน้อย เพราะอนุภาคแอลฟามีประจุบวกจะเบี่ยงเบนเมื่อกระทบกับประจุบวกที่กระจายอยู่ในอะตอม แต่แบบจำลองอะตอมของทอมสันอธิบายผลการทดลองของรัทเทอร์ฟอร์ดไม่ได้ รัทเทอร์ฟอร์ดจึงเสนอแบบจำลองอะตอมขึ้นมาใหม่ดังนี้
“อะตอมประกอบด้วยนิวเคลียสที่มีโปรตอนรวมกันอยู่ตรงกลาง นิวเคลียสมีขนาดเล็กแต่มีมวลมา และมีประจุบวก ส่วนอิเล็กตรอนซึ่งมีประจุลบและมีมวลน้อยมากวิ่งอยู่รอบ ๆ นิวเคลียส”
แบบจำลองอะตอมของรัทเทอร์ฟอร์ด
การอธิบายโครงสร้างอะตอมด้วยแบบจำลองอะตอมของรัทเทอร์ฟอร์ด
จากแบบจำลองอะตอมของรัทเทอร์ฟอร์ดสามารถอธิบายได้ว่า เมื่อผ่านอนุภาคแอลฟาซึ่งมีประจุบวกและมวลมากให้เดินทางเป็นเส้นตรงไปยังแผ่นทองคำ อนุภาคแอลฟาส่วนมากจะเคลื่อนที่ผ่านไปยังที่ว่างซึ่งมีอิเล็กตรอนเคลื่อนที่อยู่ แต่อิเล็กตรอนมีมวลน้อยมากจึงไม่มีผลต่อการเคลื่อนที่ของอนุภาคแอลฟา อนุภาคแอลฟาบางส่วนที่เคลื่อนที่ใกล้นิวเคลียสทำให้เบี่ยงเบนออกจากที่เดิม และอนุภาคที่กระทบกับนิวเคลียสซึ่งมีประจุบวกและมวลมากจึงสะท้อนกลับ การที่อนุภาคแอลฟาจำนวนน้อยมากสะท้อนกลับทำให้เชื่อว่านิวเคลียสมีขนาดเล็กมาก
แบบจำลองอะตอมของดอลตัน แบบจำลองอะตอมของทอมสัน แบบจำลองอะตอมของรัทเทอร์ฟอรด์
กลับไปที่เนื้อหา
บทเรียนที่ 5 อนุภาคในอะตอม
อนุภาคมูลฐานของอะตอม
รางวัลโนเบล (Nobel Prize) สาขาฟิสิกส์ ในปี ค.ศ.1935
United Kingdom
Liverpool University
Liverpool, United Kingdom
มีชีวิตอยู่ระหว่างปี ค.ศ.1891 -1974
ในการทดลองของรัทเทอร์ฟอร์ดสรุปว่าอะตอมมีโปรตอนและอิเล็กตรอนเป็นองค์ประกอบ ดังนั้น การคิดมวลอะตอมควรคิดจากมวลโปรตอนรวมกับมวลของอิเล็กตรอน แต่มวลของอิเล็กตรอนน้อยมาก การคิดมวลอะตอมจึงคิดจากมวลโปรตอน พบว่ามวลโปรตอน 1 โปรตอนเท่ากับ 1.7 x 10–24กรัม หรือคิดเป็น 1 หน่วยมวลอะตอม (1 amu = 1 atomic mass unit) ดังนั้นมวลอะตอมควรมีค่าเท่ากับหรือใกล้เคียงกับจำนวนโปรตอน แต่จากการทดลองกลับพบว่ามวลอะตอมจริง ๆ มีค่าเป็น 2 เท่าหรือมากกว่า 2 เท่าของจำนวนโปรตอน ในปี พ.ศ. 2463 (หรือค.ศ.1920) รัทเทอร์ฟอร์ดได้เสนอความเห็นว่าน่าจะมีอนุภาคอีกชนิดหนึ่งที่เป็นกลางทางไฟฟ้าซึ่งมีมวลใกล้เคียงกับมวลโปรตอน
ต่อมาในปี พ.ศ. 2475 (ค.ศ. 1932) เจมส์ แชดวิก (James Chadwick) ได้ค้นพบอนุภาคอีกชนิดหนึ่ง ไม่มีประจุไฟฟ้า และตั้งชื่อว่า “นิวตรอน” (neutron) นิวตรอนมีมวลมากกว่าโปรตอนเล็กน้อย โดยมีมวลเท่ากับ 1.675 x 10–24กรัม และรัทเทอร์ฟอร์ดได้เสนอว่านิวตรอนเป็นอนุภาคที่อยู่ในนิวเคลียสของอะตอม ปัจจุบันนักวิทยาศาสตร์พบว่าโปรตอนและนิวตรอนอัดกันแน่นอยู่ในนิวเคลียสยึดเหนี่ยวกันด้วยแรงนิวเคลียร์ (nuclear force) และอนุภาคที่ประกอบเป็นนิวเคลียสเรียกว่า “นิวคลีออน” (nucleon)
อนุภาคในอะตอม
ในปัจจุบันพบว่าในอะตอมประกอบด้วยอนุภาคเล็ก ๆ มากกว่า 30 ชนิด และแบ่งออกเป็น 2 ประเภท ดังนี้
1. อนุภาคที่ไม่เสถียร (unstable particles) เป็นอนุภาคที่ไม่อยู่ตัว สลายตัวได้ง่าย อนุภาคเหล่านี้เกิดจากการยิงนิวเคลียสของอะตอมด้วยอนุภาคชนิดต่าง ๆตัวอย่างอนุภาคที่ไม่เสถียรได้แก่ positron , antiproton , neutrinoเป็นต้น
2. อนุภาคที่เสถียร (stable particles) เป็นอนุภาคที่อยู่ตัว ไม่สลายตัว มี 3 ชนิดคือ โปรตอน นิวตรอน และอิเล็กตรอน เรียกอนุภาคทั้งสามว่า“อนุภาคมูลฐานของอะตอม”
| อนุภาค | สัญลักษณ์ | ประจุไฟฟ้า (C) | ชนิดประจุไฟฟ้า | มวล (กรัม) |
| อิเล็กตรอน | e |
1.602 x 10–19 |
-1 |
9.109 x 10–28 |
| โปรตอน | p |
1.602 x 10–19 |
+1 |
1.673 x 10–24 |
| นิวตรอน | n |
0 |
0 |
1.673 x 10–24 |
เลขอะตอม เลขมวล และสัญลักษณ์นิวเคลียร์
1. เลขอะตอม (Atomic number)
คือตัวเลขที่แสดงจำนวนโปรตอนของธาตุ ใช้สัญลักษณ์Zนักวิทยาศาสตร์คนแรกที่หาเลขอะตอมได้คือ เฮนรี โมสลีย์ เป็นนักวิทยาศาสตร์ชาวอังกฤษ เลขอะตอมเป็นค่าเฉพาะสำหรับธาตุหนึ่ง ๆ ธาตุแต่ละชนิดมีเลขอะตอมไม่ซ้ำกัน ดังนั้นเลขอะตอมจึงบอกชนิดของธาตุได้
2. เลขมวล (Mass number)
คือตัวเลขที่แสดงผลรวมของจำนวนโปรตอนและจำนวนนิวตรอน มีสัญลักษณ์Aเลขมวลจะมีค่าใกล้เคียงกับมวลอะตอม (Atomic mass) แต่เลขมวลเป็นเลขจำนวนเต็มเสมอ ส่วนมวลอะตอมอาจเป็นจำนวนเต็มหรือทศนิยมก็ได้ และเลขมวลไม่เป็นค่าเฉพาะสำหรับธาตุ ธาตุต่างชนิดกันอาจมีเลขมวลเท่ากันได้
|
เลขมวล |
= |
จำนวนโปรตอน + จำนวนนิวตรอน |
3. สัญลักษณ์นิวเคลียร์ (nuclear symbol)
เป็นสัญลักษณ์ที่แสดงให้ทราบว่าอะตอมของธาตุ 1 อะตอมประกอบด้วยอนุภาคมูลฐานอย่างละกี่อนุภาค โดยเขียนสัญลักษณ์ของธาตุซึ่งแสดงเลขมวลที่มุมบนด้านซ้าย และเขียนเลขอะตอมที่มุมล่างด้านซ้าย เช่น
p = 12 p = 6 p = 8
e–= 12 e–= 6 e–= 10
n = 12 n = 6 n = 8
จากสัญลักษณ์นิวเคลียร์ทำให้ทราบจำนวนอนุภาคมูลฐานของอะตอม โดยจำนวนโปรตอนดูจากเลขอะตอม อะตอมอยู่ในสภาพที่เป็นกลางทางไฟฟ้าจึงมีจำนวนอิเล็กตรอนเท่ากับจำนวนโปรตอน ส่วนจำนวนนิวตรอน =เลขมวล – เลขอะตอม
ไอโซโทป ไอโซโทน และไอโซบาร์
ไอโซโทป (Isotope)
หมายถึงอะตอมของธาตุชนิดเดียวกัน แต่มีเลขมวลต่างกัน หรืออะตอมของธาตุที่มีเลขอะตอมเท่ากัน แต่มีจำนวนนิวตรอนต่างกัน
อะตอมที่มีเลขมวลหรือจำนวนโปรตอนแต่ละจำนวนเรียกว่า 1 ไอโซโทป ตัวอย่างไอโซโทป เช่น ไฮโดรเจนมี 3 ไอโซโทปคือ, ,
p = 1 p = 1 p = 1
e–= 1 e–= 1 e–= 1
n = 0 n = 1 n = 2
protium (H) deuterium (D) tritium (T)
ไอโซโทน (Isotone)
หมายถึงอะตอมของธาตุต่างชนิดกัน มีเลขอะตอมและเลขมวลต่างกัน แต่มีจำนวนนิวตรอนเท่ากัน
p = 6 p = 7
e–= 6 e–= 7
n = 7 * n = 7 *
ไอโซบาร์ (Isobar)
หมายถึงอะตอมของธาตุต่างชนิดกัน แต่มีเลขมวลเท่ากัน
p = 6 p = 7
e–= 6 e–= 7
n = 8 n = 7
ตารางที่ 1 สรุปความหมายของไอโซโทป ไอโซโทน ไอโซบาร์
|
ชนิด |
เลขอะตอม |
เลขมวล |
จำนวนนิวตรอน |
จำนวนโปรตอน |
ชนิดของธาตุ |
|
ไอโซโทป |
เท่ากัน |
ต่างกัน |
ต่างกัน |
เท่ากัน |
ชนิดเดียวกัน |
|
ไอโซโทน |
ต่างกัน |
ต่างกัน |
เท่ากัน |
ต่างกัน |
ต่างชนิดกัน |
|
ไอโซโทน |
ต่างกัน |
เท่ากัน |
ต่างกัน |
ต่างกัน |
ต่างชนิดกัน |
กลับไปที่เนื้อหา
บทเรียนที่ 6 คลื่นและสมบัติของแสง
คลื่นและสมบัติของแสง
จากแบบจำลองอะตอมของรัทเทอร์ฟอร์ดทำให้ทราบถึงการจัดโครงสร้างของอนุภาคต่าง ๆ ในนิวเคลียส แต่ไม่ได้อธิบายว่าอิเล็กตรอนรอบนิวเคลียสอยู่ในลักษณะใด นักวิทยาศาสตร์ในลำดับต่อมาได้หาวิธีทดลองเพื่อรวบรวมข้อมูลเกี่ยวกับตำแหน่งของอิเล็กตรอนที่อยู่รอบนิวเคลียส วิธีหนึ่งก็คือการศึกษาสมบัติและปรากฏการณ์ของคลื่นและแสง แล้วนำมาสร้างเป็นแบบจำลอง
คลื่นชนิดต่าง ๆ เช่น คลื่นแสง คลื่นเสียง มีสมบัติสำคัญ 2 ประการ คือ ความยาวคลื่นและความถี่
คลื่นแสงเป็นคลื่นแม่เหล็กไฟฟ้าที่มีความถี่และความยาวคลื่นต่าง ๆ กัน ดังรูปต่อไปนี้
แสงที่ประสาทตาคนรับได้เรียกว่า“แสงที่มองเห็นได้”(visible light) ซึ่งมีความยาวคลื่นอยู่ในช่วง 400 – 700nmแสงในช่วงคลื่นนี้ประกอบด้วยแสงสีต่าง ๆ กัน ตามปกติประสาทตาของคนสามารถสัมผัสแสงบางช่วงคลื่นที่ส่องมาจากดวงอาทิตย์ได้ แต่ไม่สามารถแยกเป็นสีต่าง ๆ จึงมองเห็นเป็นสีรวมกันซึ่งเรียกว่า“แสงขาว”
กลับไปที่เนื้อหา
บทเรียนที่ 7 สเปกตรัมเกิดได้อย่างไร
| สเปกตรัมเกิดได้อย่างไร | |
|
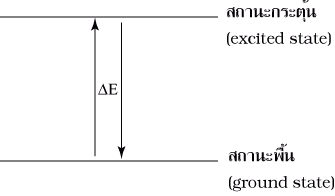
สถานะพื้น (ground state) หมายถึงอะตอมที่อิเล็กตรอนซึ่งเคลื่อนที่อยู่รอบนิวเคลียสมีพลังงานเฉพาะตัวอยู่ในระดับพลังงานต่ำ อะตอมในสถานะพื้นจะมีความเสถียรเนื่องจากมีพลังงานต่ำ สถานะกระตุ้น (excited state) หมายถึงอะตอมที่ได้รับพลังงานเพิ่มขึ้น ทำให้อิเล็กตรอนถูกกระตุ้นให้อยู่ในระดับพลังงานสูงขึ้น ที่สถานะกระตุ้นอะตอมจะไม่เสถียร เนื่องจากมีพลังงานสูง |
|
|
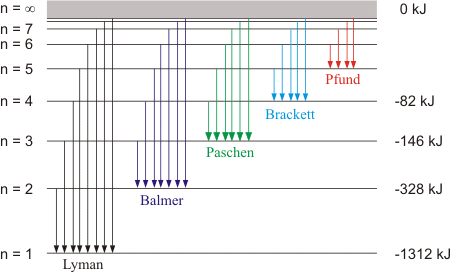
อะตอมที่ได้รับพลังงาน เช่น จากการเผา หรือจากกระแสไฟฟ้า อิเล็กตรอนจะเปลี่ยนจากสถานะพื้นไปสู่สถานะกระตุ้นซึ่งไม่เสถียร จึงต้องคายพลังงานออกมา ซึ่งพลังงานที่คายออกมาจะอยู่ในรูปพลังงานแสงหรือคลื่นแม่เหล็กไฟฟ้า เมื่อผ่านปริซึมหรือสเปกโตรสโคปจะแยกแสงออกเป็นเส้นสเปกตรัม การที่ธาตุแต่ละชนิดให้เส้นสเปกตรัมออกมาหลายเส้น แสดงว่าอิเล็กตรอนที่อยู่รอบนิวเคลียสมีหลายระดับพลังงาน ระดับพลังงานที่อยู่ใกล้นิวเคลียสจะมีพลังงานต่ำ ส่วนระดับพลังงานที่อยู่ห่างนิวเคลียสจะมีพลังงานสูง เมื่ออิเล็กตรอนคายพลังงานอาจคายพลังงานได้หลายช่วงความยาวคลื่น จึงมองเห็นเส้นสเปกตรัมได้หลายเส้น นักวิทยาศาสตร์ได้ศึกษาสเปกตรัมของแก๊ส เพราะว่ามีอะตอมอยู่ห่างกัน และใช้อะตอมไฮโดรเจนเนื่องจากมี 1 อิเล็กตรอน พบว่ามีเส้นสเปกตรัมที่ปรากฏในช่วงความยาวคลื่นที่มองเห็นได้โดยมีความยาวคลื่น 410 , 434 , 486 และ 656 นาโนเมตร ตามลำดับ นอกจากนี้การศึกษาเส้นสเปกตรัมของอะตอมของธาตุอื่นๆ ก็พบว่าอิเล็กตรอนในอะตอมของแต่ละธาตุคายพลังงานได้บางค่า และมีเส้นสเปกตรัมเฉพาะตัวไม่ซ้ำกัน โดยเส้นสีแดงมีพลังงานต่ำสุด (3.02 x 10–22kJ) และเส้นสีม่วงมีพลังงานสูงสุด (4.48 x 10–22kJ)
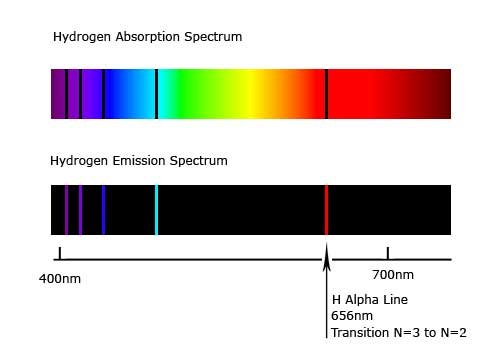
เส้นสเปกตรัมของแก๊สไฮโดรเจน (H2) การที่นักวิทยาศาสตร์ใช้อะตอมของไฮโดรเจนเป็นตัวอย่างในการแปลความหมายของเส้นสเปกตรัม เพราะเป็นอะตอมที่มีอิเล็กตรอนเดียว จากการทดลองหลายครั้งพบว่าอะตอมของไฮโดรเจนให้เส้นสเปกตรัมได้หลายเส้นที่มีลักษณะเหมือนกันทุกครั้ง จึงสรุปได้ว่าอิเล็กตรอนในอะตอมของไฮโดรเจนขึ้นไปอยู่ในสถานะกระตุ้นที่มีพลังงานแตะต่างกันได้หลายระดับ ค่าพลังงานของเส้นสเปกตรัมแสดงให้เห็นถึงการเปลี่ยนระดับพลังงานของอิเล็กตรอนในอะตอมจากระดับพลังงานสูงมายังระดับพลังงานต่ำ
Lyman series เป็นอนุกรมของเส้นสเปกตรัมของอะตอมไฮโดรเจน ซึ่งแสดงการเปลี่ยนแปลงพลังงานระหว่างสถานะพื้นกับสถานะกระตุ้น ตารางแสดงความยาวคลื่นและพลังงานของเส้นสเปกตรัม
จากข้อมูลในตาราง แสดงว่าอะตอมของไฮโดรเจนมีพลังงานหลายระดับและความแตกต่างระหว่างพลังงานของแต่ละระดับที่อยู่ถัดไปก็ไม่เท่ากัน ความแตกต่างของพลังงานจะมีค่าน้อยลงเมื่อระดับพลังงานสูงขึ้น จากเหตุผลที่อธิบายมานี้ช่วยให้สรุปได้ว่า |
||||||||||||||||||||||||||||||||||
|
1. เมื่ออิเล็กตรอนได้รับพลังงานในปริมาณที่เหมาะสม อิเล็กตรอนจะขึ้นไปอยู่ในระดับพลังงานที่สูงกว่าระดับพลังงานเดิม แต่จะอยู่ในระดับใดขึ้นกับปริมาณพลังงานที่ได้รับ การที่อิเล็กตรอนขึ้นไปอยู่ในระดับพลังงานใหม่ทำให้อะตอมไม่เสถียร อิเล็กตรอนจะกลับมาอยู่ในระดับพลังงานที่ต่ำกว่า ซึ่งในการเปลี่ยนตำแหน่งนี้อิเล็กตรอนจะคายพลังงานออกมา การดูดหรือคายพลังงานจะต้องมีค่าเฉพาะตามทฤษฎีของพลังค์ โดยค่าต่ำสุดจะเท่ากับความถี่ของอิเล็กตรอนนั้นคูณด้วยค่าคงที่ของพลังค์ 2. การเปลี่ยนระดับพลังงานของอิเล็กตรอนไม่จำเป็นต้องเปลี่ยนไปยังระดับพลังงานที่อยู่ติดกันอาจมีการเปลี่ยนข้ามระดับได้ แต่เมื่ออิเล็กตรอนรับพลังงานแล้วจะขึ้นไปอยู่ระหว่างระดับพลังงานไม่ได้ จะต้องขึ้นไปอยู่ในระดับใดระดับหนึ่งเสมอ 3. ผลต่างของพลังงานระหว่างระดับพลังงานต่ำจะมีค่ามากกว่าผลต่างของพลังงานระหว่างระดับพลังงานที่สูงขึ้นไป |
|
|||||||||||||||||||||||||||||||||
|
Niels Bohr
|
||||||||||||||||||||||||||||||||||
แบบจำลองอะตอมของโบร์
|
|
กลับไปที่เนื้อหา
บทเรียนที่ 8 แบบจำลองอะตอมแบบกลุ่มหมอก
แบบจำลองอะตอมแบบกลุ่มหมอก
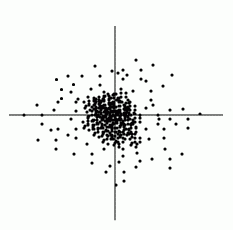
เนื่องจากแบบจำลองอะตอมของโบร์ (Niels Bohr) มีข้อจำกัดที่ไม่สามารถใช้อธิบายสเปกตรัมของอะตอมที่มีหลายอิเล็กตรอน ได้มีการศึกษาเพิ่มเติมจนได้ข้อมูลที่เชื่อว่าอิเล็กตรอนมีสมบัติเป็นทั้งอนุภาคและคลื่น โดยเคลื่อนที่รอบนิวเคลียสในลักษณะของคลื่นนิ่ง บริเวณที่พบอิเล็กตรอนได้พบได้หลายลักษณะเป็นรูปทรงต่าง ๆ ตามระดับพลังงานของอิเล็กตรอน จากการใช้ความรู้ทางกลศาสตร์ควอนตัมสร้างสมการขึ้นเพื่อคำนวณหาโอกาสที่จะพบอิเล็กตรอนในระดับพลังงานต่าง ๆ พบว่าแบบจำลองนี้อธิบายเส้นสเปกตรัมได้ดีกว่าแบบจำลองอะตอมของโบร์ โดยแบบจำลองอะตอมแบบกลุ่มหมอกกล่าวไว้ดังนี้
1. อิเล็กตรอนมีขนาดเล็กมากและเคลื่อนที่อย่างรวดเร็วตลอดเวลาไปทั่วทั้งอะตอม จึงไม่สามารถบอกตำแหน่งที่แน่นอนของอะตอมได้
2. มีโอกาสที่จะพบอิเล็กตรอนรอบนิวเคลียสบางบริเวณเท่านั้น ทำให้สร้างมโนภาพได้ว่าอะตอมประกอบด้วยกลุ่มหมอกของอิเล็กตรอนรอบ ๆ นิวเคลียส
3. บริเวณที่กลุ่มหมอกทึบแสดงว่าโอกาสที่จะพบอิเล็กตรอนได้มากกว่าบริเวณที่มีกลุ่มหมอกจาง”
การแสดงแบบจำลองอะตอมในลักษณะที่แสดงถึงความหนาแน่นของอิเล็กตรอนทำได้ยาก แต่จะแสดงในลักษณะที่เป็นลูกกลมแทน เช่น ลูกปิงปองหรือลูกกลมพลาสติก เพื่อให้สะดวกต่อการจินตนาการถึงอะตอมของธาตุได้ง่าย
ในปี ค.ศ. 1924 หลุยส์ เดอ บรอยส์ (Lois de Brolie) ให้ความเห็นว่า “ถ้าแสงมีพฤติกรรมคล้ายกับว่าประกอบด้วยอนุภาคเล็ก ๆ (โฟตอน : photon) ดังนั้นอนุภาคขนาดเล็กก็สามารถประพฤติตัวได้ทำนองเดียวกัน คือมีสมบัติเป็นได้ทั้งคลื่นและอนุภาค” ด้วยสมมติฐานนี้ ทำให้โครงสร้างของอะตอมมีความกระจ่างชัดมากขึ้นและสามารถเข้าใจปรากฏการณ์บางอย่างที่ขัดต่อทฤษฎีอะตอมของโบร์ได้ เช่น อธิบายได้ว่าเพราะเหตุใดอิเล็กตรอนจึงไม่ถูกโปรตอนดึงดูดเข้าไปในนิวเคลียส โดยพิจารณาว่าอิเล็กตรอนประพฤติตัวเป็นคลื่นนิ่งรอบนิวเคลียสนั่นเอง และอธิบายได้ว่าในการเกิดพันธะเคมี เพราะเหตุใดอิเล็กตรอนจึงเข้าคู่กันได้โดยไม่ผลักกัน โดยให้พิจารราว่าอิเล็กตรอนเป็นคลื่นซึ่งสามารถเกิดการแทรกสอดกันได้
เมื่อให้อิเล็กตรอนเคลื่อนที่รอบนิวเคลียสในวงโคจรที่เสถียรคือเป็นคลื่นนิ่ง ความยาวของเส้นรอบวงจะมีค่าเป็นจำนวนเท่าของความยาวคลื่นของอิเล็กตรอนนั้น ซึ่งสอดคล้องกับทฤษฎีของโบร์ ระดับชั้นของวงโคจรแบ่งเป็นชุดหลักได้เป็นระดับชั้น (shell) K , L , M , N , O , . . . หรือเรียกว่าระดับพลังงานที่ 1 , 2 , 3 , . . . ตามลำดับโดยที่ระดับพลังงานที่ 1 จะมีค่าพลังงานต่ำสุด นั่นคือจะต้องใช้พลังงานมากที่สุดในการดึงอิเล็กตรอนออกจากอะตอม เนื่องจากมีวงโคจรอยู่ใกล้กับนิวเคลียสมากที่สุด และในแต่ละระดับชั้นจะมีอิเล็กตรอนเป็นจำนวนไม่เกิน 2n2คือมีจำนวนเป็น 2 , 8 , 18 , 32 ตามลำดับ (เมื่อ n คือระดับพลังงาน) โดยอิเล็กตรอนชั้นนอกสุด (valence electron) จะมีได้ไม่เกิน 8 อิเล็กตรอน
ตารางแสดงระดับพลังงานหลักและระดับพลังงานย่อย
|
ระดับพลังงานหลัก (n) |
ระดับพลังงานย่อย (l) |
ชื่อของระดับพลังงานย่อย |
|
1 |
0 |
s |
|
2 |
0 , 1 |
s , p |
|
3 |
0 , 1 , 2 |
s , p , d |
|
4 |
0 , 1 , 2 , 3 |
s , p , d , f |
|
5 |
0 , 1 , 2 , 3 , 4 |
s , p , d , f , g |
ระดับพลังงานย่อย s , p , d , f สามารถบรรจุอิเล็กตรอนได้ 2 , 6 , 10 , 14 อิเล็กตรอนตามลำดับ โดยอิเล็กตรอนจะอยู่ด้วยกันเป็นคู่กระจายอยู่ในออร์บิทัล (orbital) หรือระดับพลังงานที่เป็นค่าโมเมนตัมเชิงแม่เหล็ก (m) ที่ระดับพลังงานย่อย s , p , d และ f กระจายออกมา โดยค่าโมเมนตัมเชิงแม่เหล็กจะมีค่าตั้งแต่ – l ถึง l
| เมื่อ l = 0 m = 0 | s | ||
| เมื่อ l = 1 m = –1 , 0 , 1 | p | ||
| เมื่อ l = 2 m = –2 , –1 , 0 , 1 , 2 | d | ||
| เมื่อ l = 3 m = –3 , –2 , –1 , 0 , 1 , 2 , 3 | f | ||
| เมื่อ l = 4 m = –4 , –3 , –2 , –1 , 0 , 1 , 2 , 3 , 4 | g |
| แทน ออร์บิทัล | แทน คู่อิเล็กตรอน |
ระดับพลังงานย่อย s , p , d และ f จึงบรรจุอิเล็กตรอนได้ 2 , 6 , 10 , 14 อิเล็กตรอน ตามลำดับ ส่วนอิเล็กตรอนที่เข้าคู่กันนั้นจะมีทิศทางการหมุนตรงข้ามกัน (s) เพื่อให้เกิดการดึงดูดทางแม่เหล็กกันได้ จึงมีการหมุนเป็น 2 ค่า คือ + และ –
ดังนั้นแต่ละอิเล็กตรอนจะมีค่าพลังงานที่ไม่ซ้ำกันเลย พิจารณาจากตัวเลขระดับพลังงานต่าง ๆ ได้แก่ ระดับพลังงานหลัก ระดับพลังงานย่อย ค่าโมเมนตัมเชิงแม่เหล็ก และการหมุนของอิเล็กตรอน ซึ่งเรียกตัวเลขจ่าง ๆ นี้ว่า “เลขควอนตัม” (quantum number) และจะเรียกระดับพลังงานต่าง ๆ โดยระบุระดับพลังงานหลักและระดับพลังงานย่อย เช่น 2s คือระดับพลังงานย่อย s ที่อยู่ในระดับพลังงานหลัก n = 2 เป็นต้น
ตารางแสดงระดับพลังงาน โมเมนตัวเชิงแม่เหล็ก และออร์บิทัล
|
ระดับพลังงานหลัก (n) |
ระดับพลังงานย่อย (l) |
โมเมนตัมเชิงแม่เหล็ก (m) |
ชื่อออร์บิทัล |
จำนวนออร์บิทัล |
|
1 |
0 |
0 |
1s |
1 |
|
2 |
0 |
0 |
2s |
1 |
|
1 |
–1 , 0 , 1 |
2p |
3 |
|
|
3 |
0 |
0 |
3s |
1 |
|
1 |
–1 , 0 , 1 |
3p |
3 |
|
|
2 |
–2 , –1 , 0 , 1 , 2 |
3d |
5 |
|
|
4 |
0 |
0 |
4s |
1 |
|
1 |
–1 , 0 , 1 |
4p |
3 |
|
|
2 |
–2 , –1 , 0 , 1 , 2 |
4d |
5 |
|
|
3 |
–3 , –2 , –1 , 0 , 1 , 2 , 3 |
4f |
7 |
|
|
5 |
0 |
0 |
5s |
1 |
|
1 |
–1 , 0 , 1 |
5p |
3 |
|
|
2 |
–2 , –1 , 0 , 1 , 2 |
5d |
5 |
|
|
3 |
–3 , –2 , –1 , 0 , 1 , 2 , 3 |
5f |
7 |
|
|
4 |
–4 , –3 , –2 , –1 , 0 , 1 , 2 , 3 , 4 |
5g |
9 |
สำหรับการจัดอิเล็กตรอนลงในระดับพลังงานต่าง ๆ ของอะตอมนั้นสามารถทำได้ใน 2 ลักษณะ คืออย่างง่าย โดยการจัดเรียงเข้าในระดับพลังงานหลัก และอย่างละเอียด โดยการจัดเรียงที่พิจารราถึงระดับพลังงานย่อยด้วย ซึ่งสามารถอธิบายปรากฏการณ์ต่าง ๆ ได้ดีและแม่นยำ
กลับไปที่เนื้อหา
บทเรียนที่ 9 การจัดเรียงอิเล้กตรอนในอะตอม
การจัดอิเล็กตรอนในอะตอม (Electronic configuration)
จากแบบจำลองอะตอมโดยใช้สมการคลื่น ซึ่งเป็นสมการคณิตศาสตร์ขั้นสูงคำนวณค่าพลังงานองอิเล็กตรอน พบว่าโปรตอนและนิวตรอนอยู่รวมกันในนิวเคลียส และมีอิเล็กตรอนอยู่รอบ ๆ โดยอยู่ในระดับพลังงานต่าง ๆ กัน ซึ่งพบความสัมพันธ์ดังนี้
1. การจัดอิเล็กตรอนในระดับพลังงานหลัก
จำนวนอิเล็กตรอนในแต่ละระดับพลังงานหลักมีจำนวนไม่เกิน 2n2
เมื่อ n คือระดับพลังงานหลักที่ 1 , 2 , 3 , . . .
ระดับพลังงานหลัก n=1 มีอิเล็กตรอนไม่เกิน 2อิเล็กตรอน
ระดับพลังงานหลัก n=2 มีอิเล็กตรอนไม่เกิน 8 อิเล็กตรอน
ระดับพลังงานหลัก n=3มีอิเล็กตรอนไม่เกิน 18 อิเล็กตรอน
ระดับพลังงานหลัก n=4มีอิเล็กตรอนไม่เกิน 32 อิเล็กตรอน
ตามความสัมพันธ์นี้การจัดอิเล็กตรอนในแต่ละระดับพลังงาน จะมีอิเล็กตรอนได้ไม่เกินจำนวนสูงสุดที่จะมีได้ ถ้าพิจารณา K และ Ca ซึ่งควรมีอิเล็กตรอนเป็น 2 , 8 , 9 และ 2 , 8 , 10 เนื่องจากในระดับพลังงานที่ 3 มีได้ถึง 18 อิเล็กตรอน แต่จากการศึกษาพบว่าการจัดอิเล็กตรอนของ K = 2 , 8 , 8 , 1 และ Ca = 2 , 8 , 8 , 2 เนื่องจากอิเล็กตรอนในระดับพลังงานที่ 3 ของทั้งสองธาตุมีเพียง 8 อิเล็กตรอน และส่วนที่เพิ่มขึ้นมาอีก 1 หรือ 2 อิเล็กตรอนนั้นเข้าไปอยู่ในระดับพลังงานที่ 4 เพราะการจัดอิเล็กตรอน อิเล็กตรอนชั้นนอกสุดซึ่งเรียกว่าเวเลนซ์อิเล็กตรอนต้องไม่เกิน 8
|
1 |
2 |
||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
ตารางแสดงการจัดอิเล็กตรอนในระดับพลังงานหลัก
|
ธาตุ |
เลขอะตอม |
จำนวนอิเล็กตรอนในระดับพลังงาน |
แสดงการจัดในระดับพลังงานหลัก |
|||
|
n=1 |
n=2 |
n=3 |
n=4 |
|||
|
H |
1 |
1 |
1 |
|||
|
He |
2 |
2 |
2 |
|||
|
Li |
3 |
2 |
1 |
2 , 1 |
||
|
Be |
4 |
2 |
2 |
2 , 2 |
||
|
B |
5 |
2 |
3 |
2 , 3 |
||
|
C |
6 |
2 |
4 |
2 , 4 |
||
|
N |
7 |
2 |
5 |
2 , 5 |
||
|
O |
8 |
2 |
6 |
2 , 6 |
||
|
F |
9 |
2 |
7 |
2 , 7 |
||
|
Ne |
10 |
2 |
8 |
2 , 8 |
||
|
Na |
11 |
2 |
8 |
1 |
2 , 8 , 1 |
|
|
Mg |
12 |
2 |
8 |
2 |
2 , 8 , 2 |
|
|
Al |
13 |
2 |
8 |
3 |
2 , 8 , 3 |
|
|
Si |
14 |
2 |
8 |
4 |
2 , 8 , 4 |
|
|
P |
15 |
2 |
8 |
5 |
2 , 8 , 5 |
|
|
S |
16 |
2 |
8 |
6 |
2 , 8 , 6 |
|
|
Cl |
17 |
2 |
8 |
7 |
2 , 8 , 7 |
|
|
Ar |
18 |
2 |
8 |
8 |
2 , 8 , 8 |
|
|
K |
19 |
2 |
8 |
8 |
1 |
2 , 8 , 8 , 1 |
|
Ca |
20 |
2 |
8 |
8 |
2 |
2 , 8 , 8 , 2 |
กลับไปที่เนื้อหา
บทเรียนที่ 10 การจัดเรื่องอิเล็กตรอนในอะตอม(ต่อ)
การจัดเรียงอิเล็กตรอนในอะตอม
จากการศึกษาแบบจำลองอะตอมโดยใช้สมการทางคณิตศาสตร์ขั้นสูงที่เรียกว่าสมการคลื่น คำนวณหาค่าพลังงานอิเล็กตรอน ทำให้ทราบว่าอะตอมประกอบด้วยโปรตอนและนิวตรอนอยู่รวมกันในนิวเคลียส โดยมีอิเล็กตรอนเคลื่อนที่อยู่รอบ ๆ และอยู่ในระดับพลังงานต่างกัน อิเล็กตรอนเหล่านั้นอยู่กันอย่างไร ในแต่ละระดับพลังงานจะมีจำนวนอิเล็กตรอนสูงสุดเท่าใด ให้นักเรียนพิจารณาข้อมูลจากตารางแสดงการจัดเรียงอิเล็กตรอนของธาตุบางธาตุ ดังตาราง1.4
ตารางแสดงการจัดอิเล็กตรอนของธาตุบางธาตุ
|
||||||||||||||||
เมื่อพิจารณาข้อมูลในตาราง 1.4จะพบว่าจำนวนอิเล็กตรอนในระดับพลังงานที่1มีได้มากที่สุด2 อิเล็กตรอนระดับพลังงานที่2มีได้มากที่สุด2 อิเล็กตรอนสำหรับระดับพลังงานที่3 นั้น จากการสืบค้นข้อมูลเพิ่มเติมทำให้ทราบว่ามีได้มากที่สุด18อิเล็กตรอน นั่นคือ แต่ละระดับพลังงานมีอิเล็กตรอนสูงสุด= 2n2กำหนดให้n =ระดับพลังงานของอิเล็กตรอนดังตาราง1.5
ตาราง 1.5 ตารางแสดงการบรรจุอิเล็กตรอนในระดับพลังงานหลัก
|
ระดับพลังงานที่(n) |
1 |
2 |
3 |
4 |
5 |
6 |
|
จำนวนอิเล็กตรอนที่มีได้มากที่สุด(2n2) |
2 |
8 |
18 |
32 |
32 |
32 |
จากตารางจะเห็นว่า สูตร2n2ใช้ได้ไม่เกินระดับพลังงานที่n = 4
หลักเกณฑ์ในการจัดอิเล็กตรอนเข้าสู่ระดับพลังงานหลักของอะตอม
1.ต้องทราบว่าอะตอมของธาตุนั้นมีอิเล็กตรอนกี่อิเล็กตรอน โดยหาจากเลขอะตอม(Z)
2.ต้องจัดอิเล็กตรอนเข้าไปในระดับพลังงานที่n = 1ให้เต็มก่อน เมื่อเต็มแล้วจึงจัดเข้าสู่ระดับพลังงานn = 2 n = 3ไป ตามลำดับ โดยจำนวนอิเล็กตรอนที่มีได้มากที่สุดในแต่ละระดับพลังงานเท่ากับ2n2แต่ระดับพลังงานไม่เกินn = 4
3.จำนวนอิเล็กตรอนในระดับพลังงานนอกสุดมีได้ไม่เกิน8อิเล็กตรอน และเรียกอิเล็กตรอนที่อยู่ชั้นนอกสุดนี้ว่าเวเลนซ์อิเล็กตรอน
4.จำนวนอิเล็กตรอนในระดับพลังงานถัดจากวงนอกสุดเข้ามา1ระดับพลังงานของอะตอมมีได้ไม่เกิน18อิเล็กตรอน
|
ในระดับพลังงานหลักจะประกอบด้วยระดับพลังงานย่อยที่แตกต่างกันดังตาราง 1 |
||||||||||||||||||
|
||||||||||||||||||
|
จากตารางได้ข้อสังเกตว่า 1.ระดับพลังงานหลักn = 1มีเฉพาะระดับพลังงานย่อยs ระดับพลังงานหลักn = 2มีเฉพาะระดับพลังงานย่อยs, p ระดับพลังงานหลักn = 3มีเฉพาะระดับพลังงานย่อยs, p, d ระดับพลังงานหลักn = 4มีเฉพาะระดับพลังงานย่อยs, p, d, f 2.ในระดับพลังงานย่อยจะมีตัวเลขข้างหน้าบอกระดับพลังงานหลัก ส่วนตัวเลขยกกำลังมุมขวาบนบอกจำนวนอิเล็กตรอนที่บรรจุได้สูงสุด เช่น 4p6หมายความว่าระดับพลังงานหลักn = 4ในระดับพลังงานย่อยp-orbitalมี6อิเล็กตรอน 4d5หมายความว่าระดับพลังงานหลักn = 4ในระดับพลังงานย่อยd-orbitalมี5อิเล็กตรอน |
จากการเรียงอิเล็กตรอนของธาตุในระดับพลังงานหลักทำให้ทราบว่า
1.จำนวนระดับพลังงานหลักของอิเล็กตรอน ทำให้ทราบว่าธาตุนั้นอยู่คาบใด ถ้าธาตุมีจำนวนระดับพลังงานของอิเล็กตรอนเท่ากัน แสดงว่าธาตุนั้นอยู่ในคาบเดียวกัน เช่น
Mgมีเลขอะตอม12มีการจัดอิเล็กตรอนในระดับพลังงานดังนี้2, 8, 2 Mgมี3ระดับพลังงาน
Sมีเลขอะตอม16มีการจัดอิเล็กตรอนในระดับพลังงานดังนี้2, 8, 6 Sมี3ระดับพลังงาน
แสดงว่าMgและSอยู่ในคาบเดียวกัน
2 จำนวนเวเลนซ์อิเล็กตรอน หรืออิเล็กตรอนที่อยู่ในระดับพลังงานนอกสุด ทำให้ทราบหมู่ของธาตุ ถ้าธาตุมีจำนวนเวเลนซ์อิเล็กตรอนเท่ากัน แสดงว่าธาตุนั้นอยู่ในหมู่เดียวกัน เช่น
Naมีเลขอะตอม11มีการจัดอิเล็กตรอนในระดับพลังงานดังนี้2, 8, 1 Naมีเวเลนซ์อิเล็กตรอนเท่ากับ1
Kมีเลขอะตอม19มีการจัดอิเล็กตรอนในระดับพลังงานดังนี้2, 8,8, 1 Kมีเวเลนซ์อิเล็กตรอนเท่ากับ
แสดงว่า ธาตุNaและKอยู่ในหมู่เดียวกัน
การจัดเรียงอิเล็กตรอนในระดับพลังงานย่อย
การจัดอิเล็กตรอนในระดับพลังงานหลัก ทำให้แต่ละระดับพลังงานมีจำนวนอิเล็กตรอนมากจึงเกิดปัญหาว่าอิเล็กตรอนเหล่านั้นอยู่ในระดับพลังงานเดียวกันได้อย่างไร ทำไมจึงไม่ผลักกัน เพื่อแก้ปัญหาดังกล่าว นักวิทยาศาสตร์จึงได้ศึกษาเกี่ยวกับระดับพลังงานย่อยเพื่อกระจายอิเล็กตรอนในแต่ละระดับพลังงานหลัก เข้าสู่ระดับพลังงานย่อย โดยอาศัยรูปแบบโคจรของอิเล็กตรอนรอบ ๆ นิวเคลียสเป็นเกณฑ์ในการแบ่งอิเล็กตรอนเป็นกลุ่มย่อย ๆ และเรียกรูปแบบวงโคจรนี้ว่าออร์บิทัล(Orbital)โดย1ออร์บิทัลจะมีอิเล็กตรอนได้ไม่เกิน2อิเล็กตรอน ระดับพลังงานย่อยมี4ระดับ คือs, p, d, fโดยระดับพลังงานย่อยมี
sมี1ออร์บิทัล บรรจุอิเล็กตรอนได้สูงสุด2อิเล็กตรอน
pมี3ออร์บิทัล บรรจุอิเล็กตรอนได้สูงสุด6อิเล็กตรอน
dมี5ออร์บิทัล บรรจุอิเล็กตรอนได้สูงสุด10อิเล็กตรอน
fมี7ออร์บิทัล บรรจุอิเล็กตรอนได้สูงสุด14อิเล็กตรอน
|
การจัดเรียงอิเล็กตรอนในระดับพลังงานย่อย 1.จัดอิเล็กตรอนในระดับพลังงานย่อยต่าง ๆ จะต้องจัดเข้าในระดับพลังงานย่อยที่มีพลังงานต่ำสุดก่อนแล้วจึงจัดเข้าสู่ระดับพลังงานย่อยที่มีพลังงานสูงขึ้น(ตามหลักของเอาฟบาว) ดังแผนผังต่อไปนี้ |
|
จากแผนภาพจัดเรียงอิเล็กตรอนเข้าสู่ระดับพลังงานย่อยได้ดังนี้ 1s 2s 2p 3s 3p 4s 3d 4p 5s 4d 5p 6s 4f 5d 6p 7s เช่น17Clมีการจัดเรียงอิเล็กตรอนในระดับพลังงานย่อย 21Seมีการจัดเรียงอิเล็กตรอนในระดับพลังงานย่อย 2.อิเล็กตรอน2ตัว ที่อยู่ในออร์บิทัลเดียวกัน จะต้องมีทิศทางการเคลื่อนที่สวนทางกันโดยแสดงทิศทางด้วยลูกศร 3.การจัดอิเล็กตรอนเข้าสู่ระดับพลังงานย่อย ถ้าอิเล็กตรอนบรรจุอยู่กึ่งหนึ่งหรือบรรจุเต็มออร์บิทัลจะมีโครงสร้างแบบเสถียรเช่น 24Crมีการจัดเรียงอิเล็กตรอนในระดับพลังงานย่อย ดังนี้ 1s2 2s2 2p6 3s2 3p6 4s1 3d5ไม่ใช่1s2 2s2 2p6 3s2 3p6 4s2 3d4 เพราะโครงสร้างแบบแรกเสถียรกว่า เพราะ4sและ3dจะบรรจุกึ่งหนึ่ง |
ข้อสังเกตที่ได้จากการใช้จัดเรียงอิเล็กตรอนในอะตอม
1.เลขอะตอมคู่จะอยู่ในหมู่คู่ เลขอะตอมคี่จะเป็นธาตุในหมู่คี่ เช่น
ธาตุ14Siจะเป็นธาตุในหมู่4
ธาตุ11Naจะเป็นธาตุในหมู่1
2.ธาตุหมู่IAและIIAตั้งแต่คาบ3ขึ้นไป จะมีจำนวนอิเล็กตรอนในระดับพลังงานถัดจากวงนอกสุดเข้ามา1ชั้นเป็น8เสมอ เช่น
11Naจะจัดเรียงอิเล็กตรอนเป็น2, 8, 1 12Mgจะจัดเรียงอิเล็กตรอนเป็น2, 8, 2
19Kจะจัดเรียงอิเล็กตรอนเป็น2, 8, 8, 1 20Caจะจัดเรียงอิเล็กตรอนเป็น2, 8, 8, 2
3.ธาตุหมู่IIIAถึงVIIIAตั้งแต่หมู่ที่IIIAคาบ4เป็นต้นไป จะมีจำนวนอิเล็กตรอนในระดับพลังงานถัดจากวงนอกสุดเข้ามา1ชั้นเป็น18เสมอ เช่น
31Ga 2, 8, 18, 3 (หมู่3คาบ4)
33As 2, 8, 18, 5 (หมู่5คาบ4)
4.ถ้าธาตุนั้นมีการจัดเรียงอิเล็กตรอนไม่เป็นไปตามข้อ2และ3คือมีจำนวนอิเล็กตรอนในระดับพลังงานถัดจากวงนอกสุดเข้ามา1ชั้น มีค่าตั้งแต่9 – 18แต่วงนอกสุดมีเวเลนซ์อิเล็กตรอนเป็น1หรือ2นักเรียนก็ทำนายได้ทันทีว่าเป็นธาตุแทรนซิชัน เช่น
29Cu 2, 8, 18, 1ไม่ใช่เป็นธาตุหมู่1แต่เป็นธาตุแทรนซิชันจัดเรียงอิเล็กตรอนเป็น2, 8,18, 1
23V 2, 8, 8, 5ไม่ใช่เป็นธาตุหมู่1แต่เป็นธาตุแทรนซิชันจัดเรียงอิเล็กตรอนเป็น2, 8,11, 2
หมายเหตุ ธาตุแทรนซิชันที่มีเลขอะตอมตั้งแต่21 – 30จะมีเวเลนซ์อิเล็กตรอนเป็น2ยกเว้นCuกับCrจะมีเวเลนซ์อิเล็กตรอนเป็น1
กลับไปที่เนื้อหา
บทเรียนที่ 10 วิวัฒนาการของการสร้างตารางธาตุ
ตารางธาตุ (Periodic Table)
เนื่องจากมีการค้นพบธาตุเป็นจำนวนมาก แต่ละธาตุอาจมีสมบัติคล้ายกันบ้าง และแตกต่างกันบ้าง จึงยากที่จะจดจำสมบัติต่าง ๆ ของแต่ละธาตุ นักวิทยาศาสตร์จึงได้หากฎเกณฑ์ต่าง ๆ มาจัดธาตุที่มีสมบัติคล้ายกันให้อยู่ในหมวดหมู่เดียวกันเพื่อง่ายต่อการศึกษา
วิวัฒนาการของการสร้างตารางธาตุ
หลังจากได้มีการค้นพบธาตุต่าง ๆ นักวิทยาศาสตร์ได้หาความสัมพันธ์ระหว่างสมบัติของธาตุ และนำมาใช้ในการจัดธาตุออกเป็นกลุ่มเป็นหลายลักษณะ
การจัดธาตุเป็นหมวดหมู่ของนักเคมียุคต่าง ๆ
พ.ศ. 2360 (ค.ศ. 1817) โยฮันน์ เดอเบอไรเนอร์ เป็นนักเคมีคนแรกที่พยายามจัดธาตุเป็นกลุ่ม ๆ ละ 3 ธาตุตามสมบัติที่คล้ายคลึงกัน เรียกว่า “ชุดสาม” และพบว่าธาตุกลางจะมีมวลอะตอมเป็นค่าเฉลี่ยของธาตุที่เหลือ ตัวอย่างธาตุชุดสามของเดอเบอไรเนอร์ เช่น Na เป็นอะตอมกลางระหว่าง Li กับ K มีมวลอะตอม 23 ซึ่งเป็นค่าเฉลี่ยของมวลอะตอมของธาตุ Li ซึ่งมีมวลอะตอม 7 กับธาตุ K ซึ่งมีมวลอะตอม 39 แต่เมื่อนำหลักของธาตุสามไปใช้กับธาตุอื่นที่มีสมบัติคล้ายกัน มวลอะตอมของธาตุกลางมิได้มีค่าเป็นค่าเฉลี่ยของมวลอะตอมของธาตุที่เหลือ หลักชุดสามของเดอเบอไรเนอร์จึงไม่เป็นที่ยอมรับ

การจัดธาตุของจอห์น นิวแลนด์
พ.ศ. 2407 (ค.ศ. 1864) นักวิทยาศาสตร์ชาวอังกฤษได้เสนอกฎการจัดธาตุเป็นหมวดหมู่ โดยเสนอว่า “ถ้าเรียงธาตุตามมวลอะตอมจากน้อยไปหามากพบว่าธาตุที่ 8 จะมีสมบัติเหมือนกับธาตุที่ 1 เสมอ” (ไม่รวม H และแก๊สเฉื่อย) การจัดของนิวแลนด์จะจัดได้ถึงธาตุ Ca เท่านั้น กฎนี้ไม่สามารถอธิบายได้ว่าเพราะเหตุใดมวลอะตอมจึงเกี่ยวข้องกับสมบัติที่คล้ายคลึงกันของธาตุ ในที่สุดจึงไม่เป็นที่ยอมรับ


John Alexander Reina Newlands
ตารางธาตุของนิวแลนด์
|
H 1 |
F 8 |
Cl 15 |
Co/Ni 22 |
Br 29 |
Pd 36 |
I 42 |
Pt/Ir 50 |
|
Li 2 |
Na 9 |
K 16 |
Cu 23 |
Rb 30 |
Ag 37 |
Cs 44 |
Tl 53 |
|
Gl 3 |
Mg 10 |
Ca 17 |
Zn 25 |
Sr 31 |
Cd 34 |
Ba/V 45 |
Pb 54 |
|
Bo 4 |
Al 11 |
Cr 18 |
Y 24 |
Ce/La 33 |
U 40 |
Ta 46 |
Th 56 |
|
C 5 |
Si 12 |
Ti 19 |
In 26 |
Zr 32 |
Sn 39 |
W 47 |
Hg 52 |
|
N 6 |
P 13 |
Mn 20 |
As 27 |
Di/Mo 34 |
Sb 41 |
Nb 48 |
Bi 55 |
|
O 7 |
S 14 |
Fe 21 |
Se 28 |
Ro/Ru 35 |
Te 43 |
Au 49 |
Os 51 |
การจัดกลุ่มธาตุของไมเออร์และเมเดเลเอฟ
ยูลิอุสโยทาร์ ไมเออร์ นักวิทยาศาสตร์ชาวเยอรมัน และเดมิทริ อิวาโนวิช เมเดเลเอฟ นักวิทยาศาสตร์ชาวรัสเซีย ได้ศึกษารายละเอียดของธาตุมากขึ้น พบว่าถ้าจัดเรียงธาตุตามมวลอะตอมจากน้อยไปหามาก ธาตุจะมีสมบัติคล้ายกันเป็นช่วง ๆ เมเดเลเอฟจึงตั้งเป็นกฎเรียกว่า “กฎพีริออดิก” โดยได้เสนอความคิดนี้ในปี พ.ศ. 2412 ก่อนที่ไมเออร์จะเสนอผลงานเพียงหนึ่งปี เพื่อเป็นเกียรติแก่เมเดเลเอฟ จึงเรียกตารางนี้ว่าตารางพีริออดิกของเมเดเลเอฟ

ยูลิอุส โลทาร์ ไมเออร์
(นักเคมีชาวเยอรมัน)
มเดเลเอฟได้นำสมบัติที่คล้ายคลึงกันของธาตุซึ่งปรากฎซ้ำกันเป็นช่วง ๆ มาพิจารณาประกอบกับการจัดเรียงธาตุตามมวลอะตอม และยังได้เว้นช่องว่างไว้สำหรับธาตุที่ยังไม่มีการค้นพบ โดยตำแหน่งของธาตุในตารางมีความสัมพันธ์กับสมบัติของธาตุ และยังได้ทำนายสมบัติของธาตุที่ยังไม่มีการค้นพบไว้ 3 ธาตุ โดยให้ชื่อว่า เอคา–โบรอน , เอคา–อะลูมินัม , เอคา–ซิลิคอน ซึ่งในเวลาต่อมาได้มีผู้ค้นพบธาตุที่เมเดเลเอฟได้ทำนายไว้ ซึ่งก็คือธาตุสแกนเดียม (Sc) แกลเลียม (Ga) และเจอร์มเเนียม (Ge) ตามลำดับ

ตารางเปรียบเทียบสมบัติของเอคา–ซิลิคอนกับเจเมเนียม
|
สมบัติ |
เอคา–ซิลิคอน |
เจอร์เมนียม |
|
มวลอะตอม |
72 |
72.6 |
|
ความหนาแน่น (g/cm3) |
5.5 |
5.47 |
|
สี |
เทาเข้ม |
เทาขาว |
|
ความหนาแน่นของออกไซด์ (g/cm3) |
EsO2= 4.7 |
GeO2= 4.70 |
|
ความหนาแน่นของคลอไรด์ (g/cm3) |
EsCl4= 1.9 |
GeCl4= 1.89 |
|
จุดเดือดสารประกอบของคลอไรด์ |
< 100OC |
86OC |
ตารางธาตุของเมเดเลเอฟยังมีปัญหาคือไม่สามารถอธิบายได้ว่าเหตุใดจึงต้องเรียงธาตุตามมวลอะตอม เนื่องจากในสมัยนั้นการศึกษาเรื่องโครงสร้างอะตอมและไอโซโทปยังไม่ชัดเจน แต่ได้มีผู้เสนอแนวคิดไว้ว่าตำแหน่งของธาตุในตารางธาตุไม่น่าจะเรียงตามมวลอะตอม แต่น่าจะขึ้นอยู่กับสมบัติอื่นที่มีความสัมพันธ์กับมวลอะตอม
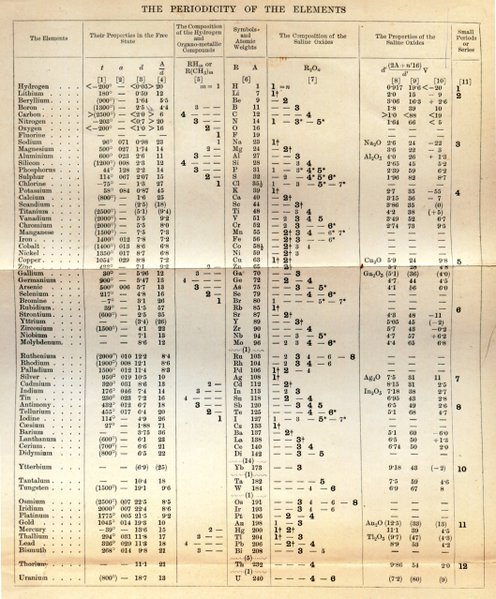
คลิกดูตารางธาตุฉบับจริงของเมเดเลเอฟ
กลับไปที่เนื้อหา
บทเรียนที่ 11 วิวัฒนการของการสร้างตารางธาตุ(ตอนจบ)
ตารางธาตุปัจจุบัน (Periodic Table)
เฮนรี โมสลีย์ ได้เสนอให้เรียงธาตุตามเลขอะตอม (เลขอะตอมคือจำนวนโปรตอน) เนื่องจากสมบัติต่าง ๆ ของธาตุมีความสัมพันธ์กับประจุบวกในนิวเคลียสหรือเลขอะตอมมากกว่ามวลอะตอม ตารางธาตุปัจจุบันจึงได้จัดเรียงธาตุตามเลขอะตอมจากน้อยไปหามาก ซึ่งมีความสอดคล้องกับกฎพีรีออดิก และพัฒนาขึ้นมาจากตารางธาตุของเมเดเลเอฟ

Henry Mosley
|
Main group |
Main gruop |
||||||||||||||||
|
IA |
IIA |
IIIA |
IVA |
VA |
VIA |
VIIA |
VIIIA |
||||||||||
|
1 |
2 |
||||||||||||||||
|
3 |
4 |
IIIB |
IVB |
VB |
VIB |
VIIB |
VIIIB |
IB |
IIB |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
11 |
12 |
Transition |
13 |
14 |
15 |
16 |
17 |
18 |
|||||||||
|
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
|
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
|
55 |
56 |
57 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
|
87 |
88 |
89 |
104 |
105 |
106 |
107 |
108 |
109 |
110 |
111 |
112 |
113 |
114 |
116 |
118 |
||
|
Lanthanide |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
|||
|
Actinide |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
|||
โดยทั่วไปธาตุในตารางธาตุแบ่งออกเป็น 4 กลุ่ม ดังนี้
1. ธาตุหมู่หลัก (main group) หรือธาตุเรพพรีเซนเททีฟ (representative element)
2. ธาตุแทรนซิชัน (transition metal)
3. กลุ่มแลนทาไนด์ (lanthanide)
4. กลุ่มแอกทิไนด์ (actinides)
ธาตุหมู่หลักประกอบด้วยโลหะที่ว่องไว (active metal) 2 หมู่ทางซ้ายของตารางธาตุ คือหมู่ IA และหมู่ IIA ถัดมาทางขวาเป็นโลหะ กึ่งโลหะ และอโลหะ ในหมู่ IIIA , IVA , VA , VIA , VIIA และ VIIIA ตามลำดับ
ธาตุแทรนซิชันเป็นธาตุพวกโลหะที่เชื่อมต่อระหว่างสองข้างที่เป็นธาตุหมู่หลักของตารางธาตุ กลุ่มแลนทาไนด์และกลุ่มแอกทิไนด์ จะอยู่ด้านล่างของตารางธาตุ ซึ่งบางครั้งเรียกธาตุสองกลุ่มนี้ว่า inner transition metals เพราะมีเลขอะตอมอยู่ระหว่างธาตุสองกลุ่มแรกในแถวล่างสุดของตารางธาตุ
หมู่ (group)
ตารางธาตุปัจจุบันแบ่งธาตุในแนวตั้งออกเป็น 18 แถว เรียกว่า “หมู่” โดยแยกออกเป็นกลุ่มย่อย A และ B กลุ่ม A มี 8 หมู่คือ IA , IIA , IIIA , IVA , VA , VIA , VIIA และ VIIIA กลุ่ม B มี 8 หมู่เช่นเดียวกัน คือ IB ถึง VIIIB ซึ่งทั้งหมดเป็นธาตุแทรนซิชัน
ธาตุในกลุ่ม A เรียกว่าธาตุหมู่หลัก (Main group หรือ representative) จะมีการจัดเรียงอิเล็กตรอนที่มีความสัมพันธ์กัน โดยธาตุที่อยู่ในหมู่เดียวกันจะมีเวเลนซ์อิเล็กตรอนเท่ากัน และตรงกับหมู่นั้น ๆ เช่น
£ ธาตุ Na เลขอะตอม 11 จัดอิเล็กตรอนเป็น 2 , 8 , 1
£ ธาตุ K เลขอะตอม 11 จัดอิเล็กตรอนเป็น 2 , 8 , 8 , 1
ดังนั้น Na และ K จึงจัดในหมู่ IA เช่นเดียวกัน
คาบ (period)
ในแนวนอนจะเรียกว่า “คาบ” ตารางธาตุมี 7 คาบ แต่ละคาบเรียงตามเลขอะตอมที่เพิ่มขึ้นตามลำดับ
คาบที่ 1 มี 2 ธาตุ คือ H , He
คาบที่ 2 และ 3 มีคาบละ 8 ธาตุ Li ถึง Ne และ K ถึง Ar ตามลำดับ
คาบที่ 4 และ 5 มีคาบละ 18 ธาตุ K ถึง Kr และ Rb ถึง Xe ตามลำดับ
คาบที่ 6 มี 32 ธาตุ แบ่งเป็น 2 กลุ่มคือกลุ่มแรก Cs ถึง Rn และกลุ่มหลังมี 14 ธาตุ คือ Ce ถึง Lu เรียกกลุ่มนี้ว่าแลนทาไนด์ (Lanthanide)
คาบที่ 7 แบ่งเป็น 2 กลุ่มคือกลุ่มแรกเป็นธาตุที่มีการค้นพบใหม่ ๆ ตลอดเวลา และกลุ่มหลังมี 14 ธาตุคือ Th ถึง Lr เรียกกลุ่มนี้ว่าแอคทีไนด์ (Actinide)
ทางด้านขวาของตารางธาตุมีเส้นทึบขั้นคล้ายขั้นบันไดแบ่งธาตุออกเป็นโลหะและอโลหะ ธาตุทางด้านซ้ายของขั้นบันไดเป็นโลหะ (metal) ทางด้านขวาเป็นอโลหะ (non–metal) ธาตุที่ติดอยู่กับขั้นบันไดทั้งทางซ้ายและทางขวาจะมีสมบัติบางประการคล้ายโลหะ และบางประการคล้ายอโลหะ เรียกธาตุเหล่านี้ว่า “ธาตุกึ่งโลหะ” (metaloid) ได้แก่ B , Si , Ge , As , Sb , Te , Po และ At
เมื่อพิจารณาการจัดอิเล็กตรอนของธาตุในตารางธาตุพบว่า
1. ธาตุที่อยู่ในแนวตั้งในกลุ่มย่อย A (หมู่เดียวกัน) จะมีเวเลนซ์อิเล็กตรอนเท่ากัน และจำนวนเวเลนซ์อิเล๋กตรอนจะตรงกับเลขหมู่
2. สำหรับธาตุตามแนวนอนที่อยู่ในแถวเดียวกัน (คาบเดียวกัน) พบว่า ธาตุในกลุ่มย่อย A มีจำนวนระดับพลังงานเท่ากัน และจำนวนระดับพลังงานจะตรงกับเลขที่คาบ เช่น
£ ธาตุ Na มีเลขอะตอม 11 จัดอิเล็กตรอนเป็น 1s2 2s22p6 3s1 ซึ่งมีจำนวนอิเล็กตรอนสูงสุดในแต่ละระดับพลังงานเป็น 2 8 1
£ ธาตุ K มีเลขอะตอม 19 จัดอิเล็กตรอนเป็น 1s2 2s22p6 3s23p6 4s1 ซึ่งมีจำนวนอิเล็กตรอนสูงสุดในแต่ละระดับพลังงานเป็น 2 8 8 1
ดังนั้นธาตุ Na และ K จึงอยู่ในหมู่ IA เพราะมีเวเลนซ์อิเล็กตรอนเท่ากับ 1
£ Na อยู่ในคาบที่ 3 เพราะมีจำนวนระดับพลังงานของอิเล็กตรอนเท่ากับ 3
£ K จะอยู่ในคาบที่ 4 เพราะมีจำนวนระดับพลังงานของอิเล็กตรอนเท่ากับ 4
กลับไปที่เนื้อหา
บทเรียนที่ 12 ขนาดอะตอม
สมบัติของธาตุตามหมู่และตามคาบ
จากการศึกษาการจัดเรียงธาตุในตารางธาตุ ช่วยให้ทราบว่าตารางธาตุในปัจจุบันจัดเป็นหมู่และคาบโดยอาศัยสมบัติบางประการที่คล้ายกัน สมบัติของธาตุตามหมู่และคาบได้แก่ ขนาดอะตอม รัศมีไอออน พลังงานไอออไนเซชัน อิเล็กโทรเนกาติวิตี สัมพรรคภาพอิเล็กตรอน จุดหลอมเหลวและจุดเดือด และเลขออกซิเดชัน จะมีแนวโน้มแปรเปลี่ยนไปตามเลขอะตอมที่เพิ่มขึ้น ซึ่งเรียกว่า “สมบัติตามตารางธาตุ” (periodic properties)
| 1. ขนาดอะตอม | |
|
|
จากการศึกษาโครงสร้างอะตอมตามทฤษฎีของโบร์ (Bohr Theory) อิเล็กตรอนในอะตอมจะมีระดับพลังงานได้หลายค่า และเมื่ออิเล็กตรอนอยู่ห่างนิวเคลียสมากก็จะยิ่งมีพลังงานสูง ดังนั้นขนาดของอะตอมจะเล็กหรือใหญ่จึงขึ้นอยู่กับอิเล็กตรอนในชั้นนอกสุดว่าอยู่ในระดับพลังงานใด และขึ้นอยู่กับจำนวนโปรตอนในนิวเคลียส ซึ่งจะมีความสัมพันธ์กับหมู่และคาบของธาตุในตารางธาตุด้วย เมื่อจะศึกษาแนวโน้มของขนาดอะตอมจึงต้องพิจารณาแนวโน้มของขนาดอะตอมตามหมู่และตามคาบ เนื่องจากแนวโน้มนี้จะแปรเปลี่ยนไปตามเลขอะตอมที่เพิ่มขึ้นและจำนวนระดับพลังงานของอิเล็กตรอน การวัดขนาดที่แน่นอนของอะตอมเป็นสิ่งที่ทำได้ยาก เพราะการกระจายของอิเล็กตรอนในอะตอมตามแบบจำลองอะตอมแบบกลุ่มหมอกนั้นบอกไม่ได้ว่าสิ้นสุดตรงไหนเพียงแต่คาดว่าเมื่อไกลนิวเคลียสออกไปมาก ๆ โอกาสที่จะพบอิเล็กตรอนมีน้อยจนเกือบเป็นศูนย์ และการที่จะแยกอะตอมออกมาเพียงอะตอมเดียวเพื่อวัดขนาดให้แน่นอนก็ทำไม่ได้เพราะอะตอมมีขนาดเล็กมาก นักเคมีมีวิธีที่จะบอกขนาดของอะตอมได้เมื่ออะตอมรวมกันเกิดเป็นโมเลกุล โดยกำหนดให้อะตอมมีรูปร่างเป็นทรงกลม การบอกขนาดอะตอมจึงบอกเป็นรัศมีอะตอม (Atomic radius) รัศมีอะตอมมี 3 แบบ คือรัศมีโคเวเลนต์ รัศมีแวนเดอร์วาลส์ และรัศมีไอออน |
| 1.1 รัศมีโคเวเลนต์ (Covalent radius) | |
|
หาได้จากระยะระหว่างนิวเคลียสของอะตอมหนึ่งกับอิเล็กตรอนที่ใช่ร่วมกันในการเกิดพันธะโคเวเลนต์ของอะตอมของธาตุชนิดเดียวกัน ในการวัดรัศมีโคเวเลนต์จะวัดระยะห่างระหว่างนิวเคลียสของ 2 อะตอมที่เกิดพันธะโคเวเลนต์ แล้วนำค่าที่ได้มาหารด้วย 2 ก็จะเป็นรัศมีโคเวเลนต์ เช่น ระยะระหว่างนิวเคลียสของ H 2 อะตอมในโมเลกุล H2 เท่ากับ 74 พิโกเมตร (pm) จะได้ว่า
ความยาวพันธะ H–H = 74 pm รัศมีโคเวเลนต์ของ H = pm = 37 pm |
|
ในโมเลกุลของคลอรีน (Cl2 ) ความยาวพันธะของ Cl–Cl เท่ากับ 198 พิโกเมตร (pm) ดังนั้น ความยาวพันธะ Cl–Cl = 198 pm รัศมีโคเวเลนต์ของ Cl = pm = 99 pm สำหรับโมเลกุลโคเวเลนต์ที่เกิดจากอะตอมต่างชนิดกัน สามารถหารัศมีโคเวเลนต์ของอะตอมชนิดหนึ่งได้ถ้าทราบรัศมีโคเวเลนต์ของอีกอะตอมหนึ่ง และทราบระยะระหว่างนิวเคลียสของอะตอมทั้งสองหรือความยาวพันธะ เช่น ถ้าต้องการหารัศมีโคเวเลนต์ของ C ใน CCl4 สามารถหาได้เมื่อทราบรัศมีโคเวเลนต์ของ Cl และทราบความยาวพันธะ C–Cl ดังนี้ ความยาวพันธะ C–Cl = 176 pm รัศมีอะตอมของ Cl = 99 pm รัศมีโคเวเลนต์ของ C = 176 – 99 pm = 77 pm |
|
1.2 รัศมีแวนเดอร์วาลส์ (Van der Waals radius) คือระยะทางครึ่งหนึ่งของระยะระหว่างนิวเคลียสของอะตอมที่อยู่ใกล้ที่สุด การวัดรัศมีแวนเดอร์วาลส์ทำโดยวัดระยะระหว่างนิวเคลียสของอะตอมที่สัมผัสกันด้วยแรงแวนเดอร์วาลส์แล้วหาร 2 อะตอมที่มาสัมผัสกันต้องเป็นอะตอมชนิดเดียวกันจึงจะหารด้วย 2 ได้ เช่น รัศมีอะตอมของ Kr หรือหาจากโมเลกุลโคเวเลนต์ 2 โมเลกุลที่มาสัมผัสกัน เช่น โมเลกุลของแก๊สไฮโดรเจน 2 โมเลกุล |
|
|
1.3 รัศมีโลหะ (Metalic radius) มีค่าเท่ากับครึ่งหนึ่งของระยะห่างระหว่างอะตอมโลหะที่อยู่ใกล้กันมากที่สุด เช่น ธาตุแมกนีเซียม มีระยะห่างระหว่างนิวเคลียสของอะตอม 2 อะตอมอยู่ใกล้กันมากที่สุดเท่ากับ 320 pm รัศมีอะตอมของโลหะ Mg = = 160 pm การศึกษารัศมีอะตอมของธาตุ ทำให้ทราบขนาดอะตอมของธาตุ และสามารถเปรียบเทียบขนาดอะตอมของธาตุที่อยู่ในคาบเดียวกันหรือในหมู่เดียวกันได้ |
แนวโน้มขนาดอะตอมตามหมู่และตามคาบ
เมื่อพิจารณาแนวโน้มของขนาดอะตอม มีแนวโน้มดังนี้
1. เมื่อพิจารณาตามคาบ ธาตุในคาบเดียวกันมีขนาดอะตอมลดลงเมื่อเลขอะตอมเพิ่มขึ้น เช่น ในคาบที่ 3 ขนาดอะตอม Na > Mg > Al > Si > P > S > Cl เป็นต้น ทั้งนี้เพราะธาตุในคาบเดียวกันมีเวเลนซ์อิเล็กตรอนอยู่ในระดับพลังงานเดียวกันแต่มีจำนวนโปตอนในนิวเคลียสต่างกัน ธาตุที่มีโปรตอนมากกว่าจะดึงดูดเวเลนซ์อิเล็กตรอนได้แรงกว่าจึงทำให้ขนาดอะตอมเล็กกว่า นั่นคือขนาดอะตอมจะลดลงจากซ้ายไปขวา
2. เมื่อพิจารณาตามหมู่ ธาตุในหมู่เดียวกันมีขนาดอะตอมเพิ่มขึ้นตามเลขอะตอม เช่น ในหมู่ IA ขนาดอะตอม Li < Na < K < Rb < Cs <Rb ทั้งนี้เพราะธาตุในหมู่เดียวกันแม้จำนวนโปรตอนในนิวเคลียสจะเพิ่มขึ้น แต่แรงดึงดูดเวเลนซ์อิเล็กตรอนมีน้อยเนื่องจากจำนวนระดับพลังงานที่มีอิเล็กตรอนอยู่เพิ่มขึ้น จึงเป็นเสมือนฉากกั้นแรงดึงดูดระหว่างโปรตอนในนิวเคลียสกับ เวเลนซ์อิเล็กตรอน มีผลทำให้ขนาดอะตอมใหญ่ขึ้นตามเลขอะตอม แสดงว่าในกรณีนี้การเพิ่มระดับพลังงานมีผลมากกว่าการเพิ่มจำนวนโปรตอนในนิวเคลียส
สำหรับธาตุในคาบที่ 4 คาบที่ 5 และคาบที่ 6 พบว่าขนาดอะตอมไม่เป็นไปตามแนวโน้มที่ต่อเนื่องกัน
กลับไปที่เนื้อหา
แบบฝึกหัดที่ 13 พลังงานไอออไนเซชัน
พลังงานไอออไนเซชัน (Ionization energy : IE)
พลังงานไอออไนเซชัน (ionization energy : IE) หมายถึงพลังงานที่น้อยที่สุดที่ใช้เพื่อทำให้อิเล็กตรอนหลุดออกจากอะตอมในสถานะแก๊สกลายเป็นไอออนในสถานะแก๊ส เช่น การทำให้โฮโดรเจนอะตอมกลายเป็นไฮโดรเจนไอออนในสถานะแก๊ส เขียนแสดงได้ดังนี้
H(g) H+(g) + e–IE = 1318 kJ/mol
ไฮโดรเจนมีเพียง 1 อิเล็กตรอน จึงมีค่าพลังงานไอออไนเซชันเพียงค่าเดียว ถ้าเป็นธาตุที่มีหลายอิเล็กตรอนก็จะมรพลังงานไอออไนเซชันหลายค่า พลังงานน้อยที่สุดที่ทำให้อิเล็กตรอนตัวแรกหลุดออกตากอะตอมในสถานะแก๊สเรียกว่า “พลังงานไอออไนเซชันลำดับที่ 1” เขียนย่อเป็น IE1พลังงานที่ทำให้อิเล็กตรอนตัวต่อ ๆ ไปหลุดออกจากอะตอมในสถานะแก๊สก็จะเรียกว่า พลังงานไอออไนเซชันลำดับที่ 2 , 3 , . . . ตามลำดับ และเขียนย่อเป็น IE2, IE3, . . . ตามลำดับ เช่น ธาตุโบรอนมี 5 อิเล็กตรอน ก็จะมีพลังงานไอออไนเซชัน 5 ค่า ดังนี้
B(g) B+(g) + e– IE = 807 kJ/mol
B+(g) B2+(g) + e– IE = 2433 kJ/mol
B2+(g) B3+(g) + e– IE = 3666 kJ/mol
B3+(g) B4+(g) + e– IE = 25033 kJ/mol
B4+(g) B5+(g) + e– IE = 32834 kJ/mol
พลังงานไอออไนเซชันกับจำนวนอิเล็กตรอนในระดับพลังงาน
ค่าพลังงานไอออไนเซชันของธาตุต่าง ๆ ในตารางธาตุใช้เป็นข้อมูลในการจัดกลุ่มอิเล็กตรอนที่อยู่รอบนิวเคลียส ซึ่งพบความสัมพันธ์คือ อิเล็กตรอนที่อยู่ในระดับพลังงานเดียวกัน (ชั้นเดียวกัน) จะมีค่าพลังงานไอออไนเซชันใกล้เคียงกัน และอิเล็กตรอนที่อยู่ต่างระดับพลังงานกัน จะมีค่าพลังงานไอออไนเซชันแตกต่างกันมาก ซึ่งสรุปความสัมพันธ์ถึงจำนวนอิเล็กตรอนในแต่ละระดับพลังงานจะมีจำนวนไม่เกิน 2n2 ตามที่ได้กล่าวมาแล้ว
การเปรียบเทียบพลังงานไอออไนเซชันของธาตุจะใช้เฉพาะ IE1ซึ่งเมื่อนำค่า IE1มาเปรียบเทียบได้ดังกราฟ
กราฟแสดงพลังงานไอออไนเซชันลำดับที่ 1
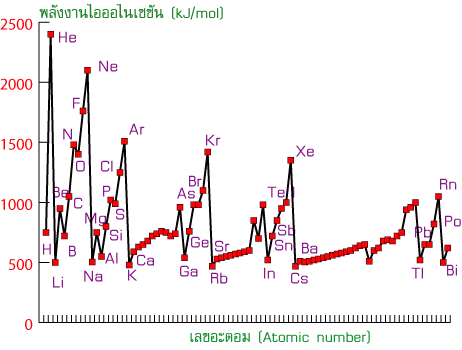
ตารางแสดงพลังงานไอออไนเซชันลำดับที่ 1
|
1 |
2 |
||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 Na |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
31 |
32 |
33 |
34 |
35 |
36 |
|
37 |
38 |
49 |
50 |
51 |
52 |
53 |
54 |
|
55 |
56 |
81 |
82 |
83 |
84 |
85 |
86 |
|
87 |
88 |
สรุปแนวโน้มพลังงานไอออไนเซชัน
1. แนวโน้มค่าพลังงานไอออไนเซชันลำดับที่ 1 ( IE1) ตามคาบ พบว่ามีแนวโน้มเพิ่มขึ้นตามเลขอะตอม เนื่องจากธาตุในคาบเดียวกันมีจำนวนโปรตอนในนิวเคลียสเพิ่มขึ้นและมีขนาดอะตอมเล็กลง แรงดึงดูดระหว่างนิวเคลียสกับเวเลนซ์อิเล็กตรอนจึงเพิ่มมากขึ้น อิเล็กตรอนจึงหลุดออกจากอะตอมได้ยาก
2. แนวโน้มค่าพลังงานไอออไนเซชันลำดับที่ 1 ( IE1) ตามหมู่ ปัจจัยทีมีผลคือคือขนาดอะตอมซึ่งเป็นผลมาจากระดับพลังงาน ค่า IE1จะลดลงเมื่ออะตอมมีขนาดใหญ่ขึ้น เพราะขนาดอะตอมที่ใหญ่ขึ้นจะมีเวเลนซ์อิเล็กตรอนที่ห่างนิวเคลียสมากขึ้น อิเล็กตรอนจะได้รับแรงดึงดูดจากนิวเคลียสน้อย อิเล็กตรอนจะหลุดออกจากอะตอมได้ง่าย
กลับไปที่เนื้อหา
บทเรียนที่ 14 อิเล็กโทรเนกาติวิตี
อิเล็กโทรเนกาติวิตี (Electronegativity : EN)
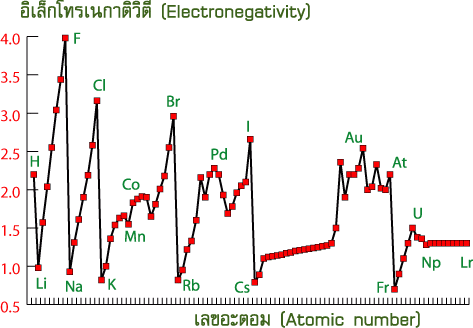
อิเล็กโทรเนกาติวิตี (electronegativity : EN) หมายถึงค่าที่แสดงความสามารถในการดึงดูดอิเล็กตรอนของอะตอมคู่ที่เกิดพันธะที่จะรวมกันเป็นโมเลกุล ธาตุที่มีค่าอิเล็กโทรเนกาติวิตีสูงตะมีความสามารถในการดึงดูดหรือรับอิเล็กตรอนได้ดี ได้แก่พวกอโลหะ ส่วนธาตุที่มีค่าอิเล็กโทรเนกาติวิตีต่ำจะดึงดูดหรือรับอิเล็กตรอนได้ไม่ดี ได้แก่พวกโลหะ เช่น โมเลกุลของ HCl เนื่องจาก Cl ดึงดูดอิเล็กตรอนได้ดีกว่า H ดังนั้น Cl จึงมีค่าอิเล็กโทรเนเติวิตีสูงกว่า H แนวโน้มค่าอิเล็กโทรเนกาติวิตีของธาตุในตารางธาตุเป็นดังนี้
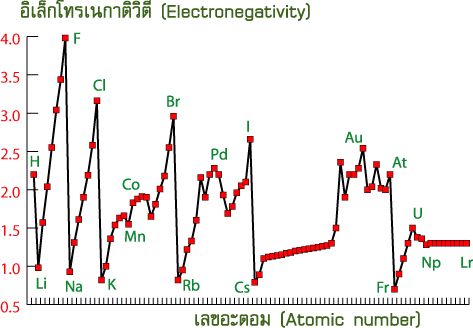
ตารางแสดงค่าอิเล็กโทรเนกาติวิตีของธาตุในตารางธาตุ
|
1 |
2 |
||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 Na |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
31 |
32 |
33 |
34 |
35 |
36 |
|
37 |
38 |
49 |
50 |
51 |
52 |
53 |
54 |
|
55 |
56 |
81 |
82 |
83 |
84 |
85 |
86 |
|
87 |
88 |
สรุปแนวโน้มค่าอิเล็กโทรเนกาติวิตี
1.แนวโน้มค่าอิเล็กโทรเนกาติวิตีตามคาบ
ปัจจัยที่มีผลคือเลขอะตอมหรือประจุบวกในนิวเคลียส ธาตุที่มีประจุบวกในนิวเคลียสมากจะมีค่า EN สูง ดังนั้นธาตุที่อยู่ในคาบเดียวกันจะมีค่า EN ดังนั้นธาตุที่อยู่ในคาบเดียวกันจะมีค่า EN เพิ่มขึ้นจากซ้ายไปขวา เพราะประจุบวกที่นิวเคลียสจะส่งแรงดึงดูดกระทำต่ออิเล็กตรอนได้มาก
2.แนวโน้มค่าอิเล็กโทรเนกาติวิตีตามหมู่
ปัจจัยที่มีผลคือขนาดอะตอมซึ่งเป็นผลมาจากจำนวนระดับพลังงาน ธาตุที่มีจำนวนระดับพลังงานน้อย หรือขนาดอะตอมเล็ก จะมีค่า EN สูงกว่าธาตุที่มีขนาดอะตอมใหญ่ในหมู่เดียวกัน เพราะอะตอมที่มีขนาดใหญ่นิวเคลียสจะส่งแรงดึงดูดออกไปที่เวเลนซ์อิเล็กตรอนได้น้อย ดังนั้น “ธาตุที่อยู่ในหมู่เดียวกันจะมีค่าENลดลงจากบนลงล่าง”
กลับไปที่เนื้อหา
บทเรียนที่ 15 สัมพรรคภาพอิเล็กตรอน
สัมพรรคภาพอิเล็กตรอน (Electron affinity : EA)
สัมพรรคภาพอิเล็กตรอน (electron affinity : EA) หมายถึงพลังงานที่อะตอมในสถานะแก๊สคายออกเมื่ออะตอมได้รับอิเล็กตรอน 1 อิเล็กตรอน ซึ่งเขียนสมการแสดงการเปลี่ยนแปลงพลังงานได้ดังนี้
A(g) + e–A–(g) + DE
EA มีค่าเป็นลบ (–) เนื่องจากมีการคายพลังงานออกมา แสดงว่าอะตอมนั้นมีแนวโน้มที่จะรับอิเล็กตรอนเข้ามาได้ดี ความสามารถในการรับอิเล็กตรอนของแต่ละธาตุมีความแตกต่างกัน ดังตัวอย่าง
F(g) + e– -------> F–(g) EA = –333 kJ/mol
O(g) + e– --------> O–(g) EA = –142 kJ/mol
P(g) + e– -------> P–(g) EA = –74 kJ/mol
จากตัวอย่างแสดงว่า F มีแนวโน้มรับอิเล็กตรอนได้สูงกว่า O และ P ตามลำดับ เมื่ออะตอมของธาตุรับ 1 อิเล็กตรอนแล้ว การรับอิเล็กตรอนเพิ่มขึ้นอีก 1 อิเล็กตรอนจะรับได้ยากขึ้น ดังนั้นค่า EA จึงมีค่าสูงขึ้นจนเป็นบวกได้ เช่น
O–(g) + e–O2–(g) EA = 780 kJ/mol
โลหะมีแนวโน้มที่จะเสียอิเล็กตรอน โดยทั่วไปค่า EA ของโลหะจึงมีค่าเป็นลบน้อย ๆ ถึงค่าบวกน้อย ๆ ดังตาราง
ตารางแสดงค่าสัมพรรคภาพอิเล็กตรอน
|
1 |
2 |
||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 Na |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
31 |
32 |
33 |
34 |
35 |
36 |
|
37 |
38 |
49 |
50 |
51 |
52 |
53 |
54 |
|
55 |
56 |
81 |
82 |
83 |
84 |
85 |
86 |
|
87 |
88 |
* ตัวเลขในวงเล๋บได้จากการคำนวณ
สรุปแนวโน้มสัมพรรคภาพอิเล็กตรอน
1. เมื่อพิจารณาตามคาบ ค่า EA ในหมู่ IA IIA และ IIIA มีค่าเป็นลบน้อยกว่าธาตุที่อยู่ทางขวามือ แสดงว่าธาตุในหมู่ดังกล่าวมีแนวโน้มที่จะรับอิเล็กตรอนได้น้อยมาก โดยเฉพาะธาตุในหมู่ IIA มีค่า EA สูงที่สุด แสดงว่ารับอิเล็กตรอนยากที่สุด
2. ธาตุหมู่ IVA VA VIA และ VIIA มีแนวโน้มสูงที่จะรับอิเล็กตรอน โดยเฉพาะธาตุหมู่ VIIA ชอบที่จะรับอิเล็กตรอนสูงที่สุด การรับอิเล็กตรอนของธาตุในหมู่ VIIA จะทำให้อะตอมมีการจัดเรียงอิเล็กตรอนเหมือนแก๊สเฉื่อยซึ่งมีความเสถียรมาก EA ของแก๊สเฉื่อยจึงมีค่าเป็นบวก
กลับไปที่เนื้อหา
บทเรียนที่ 16 จุดหลอมเหลว-จุดเดือด
จุดหลอมเหลวและจุดเดือด (Melting point , Boiling point)
สารต่าง ๆ จะมีแรงยึดเหนี่ยวระหว่างอนุภาค ซึ่งขึ้นอยู่กับว่าสารนั้น ๆ อยู่ในรูปโมเลกุลหรืออะตอม ความแข็งแรงของแรงยึดเหนี่ยวระหว่างอนุภาคจะมีผลต่อจุดหลอมเหลวและจุดเดือด สารที่ที่มีแรงยึดเหนี่ยวระหว่างอนุภาคแข็งแรงมากจุดหลอมเหลวและจุดเดือดจะสูง ส่วนสารที่มีแรงยึดเหนี่ยวระหว่างอนุภาคแข็งแรงน้อย จุดหลอมเหลวและจุดเดือดจะต่ำ
ตารางจุดหลอมเหลวและจุดเดือดของธาตุ
|
–259.1 |
–272 |
||||||
|
179 |
1280 |
2300 |
>3500 |
–209.86 |
–218 |
–223 |
–248 |
|
97.6 |
650 |
660 |
1410 |
44 |
113 |
–102 |
–248 |
|
63 |
839+2 |
29.78 |
937.4 |
358 |
217 |
–7 |
–157 |
|
39 |
770 |
156.61 |
231.9 |
631 |
450 |
114 |
–112 |
|
28 |
714 |
660+10 |
327.5 |
271.3 |
254 |
1050 |
–71 |
|
– |
700 |
สรุปแนวโน้มของจุดหลอมเหลวและจุดเดือด
1. แนวโน้มจุดหลอมเหลวและจุดเดือดตามคาบ
เมื่อพิจารณาตามคาบ ธาตุหมู่ IA IIA IIIA และ IVA จุดหลอมเหลวและจุดเดือดมีแนวโน้มสูงขึ้นตามลำดับ โดยเฉพาะหมู่ IVA จะมีจุดหลอมเหลวและจุดเดือดสูงที่สุด ส่วนหมู่ VA VIA VIIA และ VIIIA จุดหลอมเหลวและจุดเดือดต่ำ
à การที่จุดหลอมเหลวและจุดเดือดของธาตุหมู่ IA IIA และ IIIA ที่อยู่ในคาบเดียวกันมีแนวโน้มสูงขึ้นตามเลขอะตอม เนื่องจากเมื่อเลขอะตอมเพิ่มขึ้น อะตอมจะมีเวเลนซ์อิเล็กตรอนมากขึ้น รวมทั้งมีแรงยึดเหนี่ยวระหว่างนิวเคลียสกับเวเลนซ์อิเล็กตรอนที่เคลื่อนที่อิสระแข็งแรงขึ้น สำหรับธาตุหมู่ IVA บางธาตุมีโครงสร้างเป็นแบบโครงผลึกร่างตาข่าย จึงทำให้มีจุดหลอมเหลวและจุดเดือดมีค่าสูงขึ้น ซึ่งอธิบายได้อีกเหตุผลหนึ่งคืออะตอมของโลหะจะยึดเหนี่ยวกันด้วยพันธะโลหะ โดยความแข็งแรงของพันธะโลหะจะพิจารณาดังนี้
£ แปรผันตรงกับจำนวนเวเลนซ์อิเล็กตรอน ธาตุที่มีจำนวนเวเลนซ์อิเล็กตรอนมาก พันธะโลหะจะแข็งแรงมาก จุดหลอมเหลวและจุดเดือดจะสูง
£ แปรผกผันกับขนาดอะตอม ธาตุที่มีขนาดอะตอมเล็กพันธะโลหะจะแข็งแรงมาก จุดหลอมเหลวและจุดเดือดจะสูง
à ธาตุหมู่ VA VIA VIIA และ VIIIA มีจุดหลอมเหลวและจุดเดือดต่ำ และมีค่าใกล้เคียงกัน เนื่องจากแรงยึดเหนี่ยวระหว่างโมเลกุลของธาตุกลุ่มนี้มีค่าต่ำมาก โมเลกุลของอโลหะยึดเหนี่ยวกันด้วยแรงแวนเดอร์วาลส์ โดยแรงแวนเดอร์วาลส์จะแปรผันตรงกับมวลโมเลกุล และขนาดโมเลกุล
£ โมเลกุลที่มีมวลโมเลกุลสูง หรือขนาดโมเลกุลใหญ่จะมี
แรงแวนเดอร์วาลส์แข็งแรงมาก จุดหลอมเหลวและจุดเดือดจะสูง
2. แนวโน้มจุดหลอมเหลวและจุดเดือดตามหมู่
เมื่อพิจารณาตามหมู่พบว่าจุดหลอมเหลวและจุดเดือดของธาตุหมู่ IA IIA และ IIIA ส่วนใหญ่มีค่าลดลงเมื่อมีเลขอะตอมเพิ่มขึ้น หรือมีแนวโน้มลดลงจากบนลงล่างตามหมู่ เนื่องจากมีขนาดอะตอมใหญ่ขึ้น ความแข็งแรงของพันธะโลหะจะลดลงตามหมู่ ส่วนธาตุหมู่ VA VIA VIIA และ VIIIA มีจุดหลอมเหลวและจุดเดือดเพิ่มขึ้นตามเลขอะตอม ซึ่งเป็นผลมาจากมีมวลอะตอมเพิ่มขึ้น ทำให้แรงดึงดูดระหว่างโมเลกุล (แรงแวนเดอร์วาลส์) มีค่ามากขึ้น สำหรับจุดหลอมเหลวและจุดเดือดของธาตุหมู่ IVA มีแนวโน้มที่ไม่ชัดเจน เนื่องจากธาตุหมู่ IVA มีโครงสร้างและแรงยึดเหนี่ยวระหว่างอะตอมแตกต่างกัน จึงไม่สามารถสรุปแนวโน้มได้
กลับไปที่เนื้อหา
บทเรียนที่ 17 เลขออกซิเดชัน
เลขออกซิเดชัน (Oxidation number)
หมายถึงจำนวนประจุไฟฟ้าหรือประจุไฟฟ้าสมมติของไอออนหรืออะตอมของธาตุ
ในกรณีที่เป็นสารประกอบไอออนิก เลขออกซิเดชันเป็นค่าแสดงประจุไฟฟ้าของไอออน โดยอะตอมที่ให้อิเล็กตรอนจะมีเลขออกซิเดชันเป็นบวก อะตอมที่รับอิเล็กตรอนจะมีเลขออกซิเดชันเป็นลบ เช่น โซเดียมคลอไรด์ (NaCl) ประกอบด้วยโซเดียมไอออน (Na+)และคลอไรด์ไอออน (Cl-) ซึ่งเกิดจากการที่อะตอมของโซเดียมมีการเสียอิเล็กตรอนไปหนึ่งอิเล็กตรอน โซเดียมจึงมีประจุเท่ากับ +1 และคลอรีนได้รับอิเล็กตรอน 1 อิเล็กตรอน คลอรีนจึงมีประจุเป็น -1 ดังนั้นเลขออกซิเดชันของโซเดียมและคลอรีนในสารประกอบโซเดียมคลอไรด์จึงมีค่าเท่ากับ +1 และ -1 ตามลำดับ
ในกรณีสารประกอบโคเวเลนต์ซึ่งไม่มีการถ่ายโอนอิเล็กตรอนกันระหว่างอะตอม แต่มีการใช้เวเลนซ์อิเล็กตรอนร่วมกันระหว่างอะตอมของธาตุที่เป็นองค์ประกอบ เลขออกซิเดชันจึงเป็นค่าแสดงประจุไฟฟ้าสมมติของอะตอมของธาตุ ซึ่งสามารถกำหนดเลขออกซิเดชันได้โดยพิจารณาจากค่าอิเล็กโทรเนกาติวิตีของอะตอมที่ใช้อิเล็กตรอนร่วมกัน ธาตุที่มีค่าอิเล็กโทรเนกาติวิตีสูงกว่าจะดึงดูดอิเล็กตรอนเข้าใกล้นิวเคลียสได้มากกว่า จะแสดงอำนาจขั้วไฟฟ้าเป็นลบ (d-) อะตอมที่มีค่าอิเล็กโทรเนกาติวิตีต่ำกว่าจะแสดงอำนาจขั้วไฟฟ้าเป็นบวก (d+) เช่น แก๊สแอมโมเนีย (NH3) 1 โมเลกุลเกิดจากการสร้างพันธะระหว่าง N 1 อะตอม และ H 1 อะตอม โดยใช้อิเล็กตรอนร่วมกันดังนี้
| ไนโตรเจน (N) มีค่าอิเล็กโทรเนกาติวิตีสูงกว่าไฮโดรเจน (H) ดังนั้นไนโตรเจนจึงแสดงอำนาจขั้วไฟฟ้าลบ และมีเลขออกซิเดชันเป็น -3 ส่วนไฮโดรเจนแสดงอำนาจขั้วไฟฟ้าบวก และมีเลขออกซิเดชันเป็น +1 |
เกณฑ์การกำหนดค่าเลขออกซิเดชัน มีเกณฑ์ดังนี้
1. ธาตุอิสระทุกชนิดทั้งที่อยู่ในรูปอะตอมหรือโมเลกุล มีเลขออกซิเดชันเท่ากับศูนย์ เช่น Fe , Zn , H2, N2, O2, P4, S8ต่างมีเลขออกซิเดชันเท่ากับศูนย์
2. ออกซิเจนในสารประกอบทั่วไปมีเลขออกซิเดชัน -2 ยกเว้นในสารประกอบเปอร์ออกไซด์ เช่น Na2O2, H2O2, BaO2ออกซิเจนมีเลขออกซิเดชัน -1 ในสารประกอบซูเปอร์ออกไซด์ เช่น KO2ออกซิเจนมีเลขออกซิเดชัน -1/2 ในสารประกอบ OF2ออกซิเจนมีเลขออกซิเดชัน +2
3. ไฮโดรเจนในสารประกอบทั่วไปมีเลขออกซิเดชัน +1 ยกเว้นในสารประกอบโลหะไฮไดรด์ เช่น NaH ไฮโดรเจนมีเลขออกซิเดชัน -1
4. ไอออนของธาตุมีเลขออกซิเดชันเท่ากับประจุของไอออนนั้น เช่น H+เลขออกซิเดชันเท่ากับ +1 , Ca2+เลขออกซิเดชันเท่ากับ +2 , Cl-เลขออกซิเดชันเท่ากับ -1 เป็นต้น
5. ไอออนที่ประกอบด้วยอะตอมมากกว่า 1 ชนิด ผลรวมของเลขออกซิเดชันของทุกอะตอมเท่ากับประจุของไอออนนั้น เช่น Cr2O72-มีประจุ -2 ผลรวมของเลขออกซิเดชันของ Cr2O72-จึงเท่ากับ -2
6. ในสารประกอบใด ผลรวมของเลขออกซิเดชันของทุกอะตอมเท่ากับศูนย์ เช่น CaO เลขออกซิเดชันของแคลเซียมเท่ากับ +2 ของออกซิเจนเท่ากับ -2 ซึ่งรวมกันจะเท่ากับศูนย์
ตัวอย่างที่ 1 จงหาเลขออกซิเดชันของ Mn ในสารประกอบ KMnO4
|
ผลรวมเลขออกซิเดชันของ KMnO4 |
= |
0 |
|
K + Mn + 4(O) |
= |
0 |
|
(+1) + Mn + 4(-2) |
= |
0 |
|
Mn |
= |
(+8) - 1 |
|
= |
+7 |
ตัวอย่างที่ 2 จงหาเลขออกซิเดชันของ Cr ในสารประกอบ K2Cr2O7
|
ผลรวมเลขออกซิเดชันของ K2Cr2O7 |
= |
0 |
|
2K + 2Cr + 7(O) |
= |
0 |
|
2(+1) + 2Cr + 7(-2) |
= |
0 |
|
2Cr |
= |
(+14) - 2 |
|
Cr |
= |
+6 |
กลับไปที่เนื้อหา