ข้อมูลและการวิเคราะห์ข้อมูล

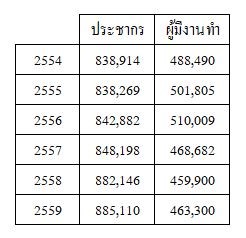
          ความก้าวหน้าของเทคโนโลยีการสื่อสารโดยเฉพาะอย่างยิ่งด้านอินเทอร์เน็ตของสรรพสิ่ง ทำให้การได้มาซึ่งข้อมูลในรูปแบบ real time ไม่ใช่เรื่องยากอีกต่อไป การใช้ข้อมูลขับเคลื่อนจึงเป็นแนวคิดใหม่สำหรับการสร้างนวัตกรรมใหม่ ๆ ในยุคปัจจุบัน ข้อมูลจึงเป็นสิ่งมีค่า แต่การใช้ข้อมูลให้เกิดประโยชน์สูงสุดนั้น เราจะต้องทำความเข้าใจข้อมูล สำรวจข้อมูลที่เรามี และจัดเตรียมข้อมูลเพื่อนำไปใช้ และถ่ายทอดในรูปแบบสารสนเทศต่อไป ประเภทของข้อมูลนั้นสามารถแบ่งได้หลายประเภท หลายรูปแบบขึ้นกับเกณฑ์ที่ใช้ในการจำแนก เช่น ข้อมูลเชิงปริมาณหรือข้อมูลเชิงคุณภาพ ข้อมูลชนิดเต็มหน่วยหรือข้อมูลชนิดต่อเนื่อง การจำแนกประเภทของข้อมูลจะช่วยให้เราสามารถเลือกเครื่องมือและทฤษฎีที่เหมาะสมในการวิเคราะห์ทำให้ได้สารสนเทศที่มีประสิทธิภาพ สำหรับการจำแนกด้วยเกณฑ์การได้มาซึ่งข้อมูลเราสามารถแบ่งได้เป็นสองประเภทได้แก่ ข้อมูลปฐมภูมิเป็นข้อมูลที่ไม่มีอยู่ก่อน เราต้องลงมือเก็บด้วยตนเอง  แต่หากข้อมูลที่เราต้องการเป็นข้อมูลที่มีอยู่ก่อนแล้วเราจะเรียกว่า ข้อมูลทุติยภูมิเช่นตารางที่ 1 เป็นข้อมูลจำนวนประชากรและจำนวนผู้มีงานทำในจังหวัดกาญจนบุรี

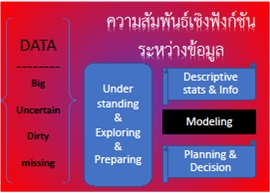
ภาพที่ 1 ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล
โดย วีระ ยุคุณธร

ตารางที่ 1 ข้อมูลจำนวนประชากรและผู้มีงานทำในจังหวัดกาญจนบุรี ปีพ.ศ. 2554 - 2559

ที่มา: แผนพัฒนาจังหวัดกาญจนบุรี 4 ปี พศ. 2557 - 2560 และ 2561 - 2564

1. ข้อมูลและการวิเคราะห์ข้อมูล

           ในทางสถิติเราจะต้องระบุการพรรณนานาให้ชัดเจนว่าหมายถึงประชากรหรือตัวอย่างโดยที่ ประชากร (population) หมายถึงคนหรือสิ่งของทั้งหมดที่เป็นไปได้ภายใต้ขอบเขตของคุณลักษณะที่เราต้องการศึกษา ตัวอย่าง (Sample) หมายถึงคนหรือวัตถุที่ถูกเลือกจากกลุ่มประชากร ในทางปฏิบัติบ่อยครั้งประชากรมีขนาดใหญ่เป็นอุปสรรคต่อการเก็บข้อมูล ดังนั้นจึงทำการศึกษากลุ่มตัวอย่างจากนั้นอนุมานค่าพารามิเตอร์หรือข้อค้นพบจากกลุ่มตัวอย่างไปสู่ประชากร ผ่านแนวคิด สถิติอนุมาน (Inferential Statistics) และเราใช้ สถิติพรรณนา (Descriptive Statistics) ในการอธิบายข้อมูลเพื่อทำความเข้าใจข้อมูลก่อนการอนุมาน 

• สถิติพรรณนา

          ในกรณีที่เรามีข้อมูลจำนวนมากแต่เราต้องการตัวแทนของข้อมูลทั้งหมดเราจะใช้ การวัดแนวโน้มสู่ส่วนกลาง (Measures of Central Tendency) ซึ่งเป็นตัวประมาณค่าของข้อมูลทั้งหมดที่มีนิยามใช้ตัววัด 3 แบบได้แก่

1. ค่าเฉลี่ย (Mean) คือผลรวมของข้อมูลทั้งหมดหารด้วยจำนวนข้อมูล เช่น เรามีข้อมูลจำนวน 5 ค่าคือ 4, 7, 2, 3, 4 จะได้ค่าเฉลี่ยเท่ากับ (4+7+2+3+4) / 5 = 4

2. ค่ามัธยฐาน (Median) คือค่าของข้อมูลที่อยู่ตำแหน่งกลาง ดังนั้นในการหาค่ามัธยฐานนั้น เราจะต้องทำการจัดเรียงข้อมูล จากนั้นหาตำแหน่งจุดกึ่งกลางของข้อมูล แล้วจึงทำการคำนวณค่า ในกรณีที่ข้อมูลมีอยู่เป็นจำนวนคี่เช่น เรามีข้อมูล 5 ข้อมูล 4, 7, 2, 3, 5 เมื่อทำการจัดเรียงแล้วจะได้ 2, 3, 4, 5, 7 ข้อมูลกึ่งอย่างอยู่ในตำแหน่งที่ (5+1)/2 = 3 ดังนั้นค่ามัธยฐานจึงเท่ากับ 4 แต่หากเรามีข้อมูลเป็นจำนวนคู่เช่นกำหนดข้อมูล 6 ค่าดังนี้ 4, 7, 2, 3, 5, 7 ทำการจัดเรียงข้อมูลจะได้ 2, 3, 4, 5, 7, 7 พบว่าตำแหน่งกึ่งกลางข้อมูลคือตำแหน่งที่ (6+1)/2 = 3.5 นั้นอยู่ระหว่างตำแหน่งที่ 3 และตำแหน่งที่ 4 ค่ามัธยฐานคือ (4+5)/2 = 4.5

3. ค่าฐานนิยม (Mode) ข้อมูลที่มีความถี่ในการเกิดสูงสุด เช่นข้อมูล 4, 7, 2, 3, 5 จะเห็นว่าไม่มีฐานนิยม แต่สำหรับข้อมูล 4, 7, 2, 3, 5, 7 จะพบว่า 7 เกิดขึ้นมากที่สุดดังนั้นฐานนิยมคือ 7 ในกรณีที่ฐานนิยมมี 2 สองค่าเราจะเรียกข้อมูลลักษณะนี้ว่า bimodal แต่ถ้าฐานนิยมมีตั้งแต่สองค่าขึ้นไปจะเรียกว่า multimodal

        สำหรับการวิเคราะห์รายละเอียดข้อมูล (Exploratory Data Analysis) เรานิยมใช้การอธิบายข้อมูลผ่านรูปภาพอาทิ พลอตแผนภาพการกระจาย (Scatter Plots) แผนภูมิแท่ง (Bar Chart) แผนภูมิวงกลม (Pie Chart) ฮิสโทแกรม (Histogram) พลอตต้นใบ (Stem and Leaf Plots) หรือ พลอตกล่อง (Box Plots) จะทำให้เราเห็นการกระจายตัวของข้อมูล (Distribution) ตลอดจนข้อมูลที่มีความผิดปกติ กระจายตัวออกจากกลุ่ม (Outlier)

• การประยุกต์ใช้สถิติพรรณนากับข้อมูล

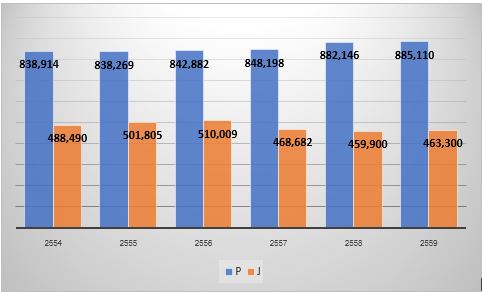
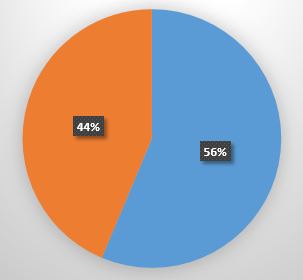
          จากตาราง 1 เราจะทำการหาค่ากลางข้อมูลประชากรและผู้มีงานทำในจังหวัดกาญจนบุรีตั้งแต่ปีพ.ศ. 2554 – 2559 แสดงเป็นกราฟแท่งได้ดังภาพที่ 2 โดยเฉลี่ยแล้วโดยมีค่าเฉลี่ยประชากร (P) ในระยะ 6 ปีอยู่ที่ 855,920 คนและมีผู้มีงานทำ (J) เฉลี่ยในระยะ 6 ปีอยู่ที่ 482,031 คิดเป็นสัดส่วนร้อยละ 56.32

ภาพที่ 2 กราฟแท่งแสดงจำนวนประชากรและผู้มีงานทำในจังหวัดกาญจนบุรีปีพ.ศ. 2554 – 2559 (ซ้าย)

และแผนภาพวงกลมแสดงสัดส่วนการมีงานทำของประชากรโดยเฉลี่ยในระยะ 6 ปี (ขวา)

ในการคำนวณบางครั้งเรานิยมใช้เทคนิค normalization กำหนดขอบเขตค่าตัวแปรหรือพารามิเตอร์ให้อยู่ในช่วง [0,1] โดยการหารด้วยค่าสูงสุดในกลุ่มข้อมูล

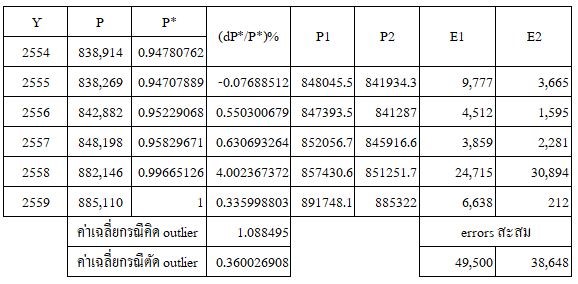
 ตารางที่ 2 การวิเคราะห์รายละเอียดข้อมูลอัตราการเพิ่มของประชากรในตารางที่ 1

          จากตารางที่ 2 ค่า P* เป็นค่าที่ได้จากการทำ normalization อัตราการเปลี่ยนแปลงประชากรนั้นจะขึ้นกับจำนวนประชากรที่มีอยู่เดิมนั้นคือ อัตราการเปลี่ยนประชากรปี 2555 จะขึ้นกับจำนวนประชากรในปี 2554 เพราะฉะนั้นอัตราการเปลี่ยนในปี 2555 คำนวณได้จาก

          dP*/P* % = [P*(2555) - P*(2554))/P*(2554] * 100%

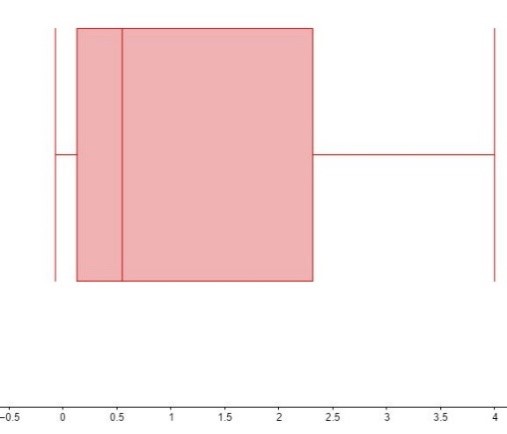
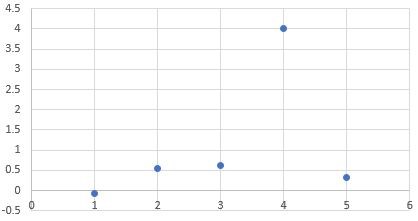
        เมื่อนำค่าดังกล่าวมาเขียน Box plot และ Scatter plot ดังภาพที่ 3 จะเห็นว่า ไม่พบ Outlier ใน Box Plot แต่หากเรามองข้อมูลในปี 2558 เป็น Outlier แล้วเราสามารถประมาณอัตราการเปลี่ยนแปลงประชากรนี้ได้ด้วยค่าคงที่ซึ่งเมื่อนำไปใช้ประมาณประชากรแล้วพบว่า P2 ประมาณได้ดีกว่า P1 (เพราะว่า errors สะสมของ E2 น้อยกว่า E1)

ภาพที่ 3 box plot ของอัตราการเปลี่ยนแปลงประชากร (ซ้าย) และ scatter plot ของอัตราการเปลี่ยนแปลงประชากร (ขวา)

การแจกแจงแบบทวินาม

          ทฤษฎีความน่าจะเป็นนั้นอยู่บนพื้นฐานของการเกิดขึ้นของเหตุการณ์ (Existence of Events) บนเซต {0, 1} โดยที่ 0 := ไม่เกิดเหตุการณ์ และ 1 := เกิดเหตุการณ์ พิจารณาการโยนเหรียญ 2 ครั้ง หากเราให้ 1 แทนการออกหัว และ 0 แทนการออกก้อย เหตุการณ์ทั้งหมดที่เป็นไปได้ (Sample Space) S = {00, 01, 10 ,11}

          2.1 ความน่าจะเป็นแบบทวินาม

          หากเราสนใจการออกหัว เหตุการณ์ทั้งหมดที่เป็นไปได้คือเซต {0, 1, 2} ถ้าเราให้ x เป็นตัวแปรของจำนวนครั้งที่ออกหัวจากการสุ่มโยนเหรียญสองครั้ง เรียก x ว่า ตัวแปรสุ่ม (Random Variable) แล้ว

          P(x = 0):= ความน่าจะเป็นที่โยนเหรียญ 2 ครั้งแล้วออกหัว 0 ครั้ง = 1/4 = 0.25

          P(x = 1):= ความน่าจะเป็นที่โยนเหรียญ 2 ครั้งแล้วออกหัว 1 ครั้ง = 2/4 = 0.5

          P(x = 2):= ความน่าจะเป็นที่โยนเหรียญ 2 ครั้งแล้วออกหัว 2 ครั้ง = 1/4 = 0.25

          P(x <= 0):= ความน่าจะเป็นที่โยนเหรียญ 2 ครั้งแล้วออกหัวไม่เกิน 0 ครั้ง = 1/4 = 0.25

          P(x <= 1):= ความน่าจะเป็นที่โยนเหรียญ 2 ครั้งแล้วออกหัวไม่เกิน 1 ครั้ง = 3/4 = 0.75

          P(x <= 2):= ความน่าจะเป็นที่โยนเหรียญ 2 ครั้งแล้วออกหัวไม่เกิน 0 ครั้ง = 4/4 = 1.00

          โดยการวางนัยยะทั่วไปแล้วความน่าจะเป็นแบบทวินามนั้นเราให้ความสนใจเกี่ยวกับจำนวนครั้งของความสำเร็จ (success) หรือ ความล้มเหลว (failure) สมมติว่าเราทำการทดลองจำนวน 10 ครั้งแต่ละครั้งมีโอกาสสำเร็จอยู่ที่ 95 % ( s = 0.95) โอกาสล้มเหลว 5 % (f = 0.05)  ถ้า x เป็นจำนวนครั้งของความสำเร็จแล้ว P(x = 6) คือความน่าจะเป็นที่ความน่าจะเป็นที่ทำการทดลองแล้วสำเร็จ 6 ครั้งแต่ล้มเหลว 4 ครั้งนั้นคือรูปแบบทั้งหมดของการจัดเรียงเชิงเส้น 6s4f = C(10,6) s⁶f⁴ = C(10,6)(0.95)⁶(0.05)⁴ เป็นไปตามทฤษฎีบททวินาม ถ้าเราทำการทดลอง n ครั้ง และมีอัตราสำเร็จและล้มเหลวเป็น s และ f ตามลำดับ แล้ว

          (s + f)ⁿ = 1

          สอดคล้องกับคุณสมบัติความน่าจะเป็น P(S) = 1    

          สำหรับการวัดค่าแนวโน้มเข้าสู่ส่วนกลางของทวินามนั้นมีสูตรดังนี้

          ค่าเฉลี่ยทวินาม (binomial mean) = E[x] = np

          ค่าความแปรปรวนทวินาม (binomial variance) = V[x] = np(1 - p)

          ค่าส่วนเบี่ยงเบนมาตรฐานทวินาม (binomial standard deviation) = sqrt{ np(1 - p) }

            ตัวอย่างเช่นสมมติมีการผลิตสินค้าจำนวน 500 ชิ้น (n = 500) ของแต่ละชิ้นจะมีโอกาสชำรุด 2% (p = 0.02) จะได้ค่าเฉลี่ยที่จะมีของชำรุดเท่ากับ np = 500*0.02 = 10 ชิ้นมีค่าความแปรรวน np(1 - p) = 500*0.98*0.02 = 9.8 และมีส่วนเบี่ยงเบนมาตรฐาน sqrt(1.96) = 3.13

          2.2 ตัวอย่างการใช้แนวคิดการแจกแจงแบบทวินามในการวิเคราะห์การติดเชื้อ

          สมมติว่าเราพิจารณากลุ่มคน 3 คนในสามคนนี้มีผู้ติดเชื้อจำนวน 1 คนและอีก 2 คนเป็นผู้ที่มีโอกาสได้รับเชื้อถ้าโอกาสการติดเชื้อเท่ากับ 40 % นั้นคือ  s = 0.4 แล้วจะมีโอกาสไม่ติดเชื้อ f = 0.6

รูปแบบของการระบาดที่เกิดจากมีผู้ติดเชื้อ 1 คนเป็นไปได้ 3 กรณีคือ x = {1,2,3} เมื่อ x เป็นตัวแปรสุ่มของจำนวนผู้ติดเชื้อในสถานการณ์ที่มีผู้ติดเชื้อ 1 คนแทนด้วย I1 อยู่ร่วมกับผู้ที่มีโอกาสติดเชื้อ 2 คนแทนด้วย S1 และ S2

          กรณีที่ 1 (x = 1) คือผลสุดท้ายแล้วมีผู้ติดเชื้อเพียงคนเดียวนั้นหมายความว่าผู้ติดเชื้อคนแรกไม่ทำให้อีกคน 2 ติดเชื้อ (I1,S1) := f และ (I1,S2) :=f P(x = 1+0 = 1) = C(2,0) 0.6² = 0.36 = 36%

          กรณีที่ 2 (x = 2) คือผลสุดท้ายแล้วมีผู้ติดเชื้อสองคนนั้นหมายความว่าผู้ติดเชื้อคนแรกทำให้มีผู้ติดเชื้อเพิ่ม 1 คน แต่ไม่ระบาดไปสู่คนที่สาม มีได้ 2 แบบคือ (I1,S1) := s , (I1,S2) := f, (S1,S2) := f หรือ (I1,S1) := f , (I1,S2) := s, (S1,S2) := f

P(x = 1+1+0 = 2) = C(2,1)(0.6)(0.4)*C(1,0)(0.4)=2(0.4)(0.6)² = 0.288 = 28.8%

            กรณีที่ 3 (x = 3) คือผลสุดท้ายแล้วมีผู้ติดเชื้อสามคนนั้นอาจเกิดจาก

           กรณีที่ 3.1 ผู้ติดเชื้อคนแรกทำให้อีก 2 คนติดเชื้อ (I1,S1) := s, (I1,S2) := s P(x = 1+2 = 3) = C(2,2)(0.4)² = 0.16 = 16%

           กรณีที่ 3.2 มีกลไกการติดเชื้อ 2 ขั้นตอนคือผู้ติดเชื้อคนแรกทำให้คนที่สองติดเชื้อ และคนที่สองเป็นคนทำให้คนที่สามติดเชื้อ (I1,S1) := s, (I1,S2) := f, (S1,S2) := s เป็นต้นดังนั้น P(x = 1+1+1 = 3) = C(2,1)(0.4)(0.6) * C(1,1)(0.4) = 2(0.4)²(0.6) = 0.192 = 19.2% รวมกรณีที่ 3 จะพบว่า P(x = 3) = P(x = 1+2) + P(x = 1 + 1 + 1) = 16% + 19.2% = 35.2%

            ถ้าสมมติให้มีกลุ่มขนาด 3 คนจำนวน 5,000 กลุ่มคาดว่า

     (C1) กลุ่มที่มีผู้ติดเชื้อ 1 คนมีจำนวนE[x = 1] = nP(x = 1) = 5000*36% = 1,800 กลุ่ม มีค่าความแปรปรวน V[x=1] = 5000*36%*64% = 1,152 กลุ่ม และส่วนเบี่ยงเบนมาตรฐาน 33.94 กลุ่ม

     (C2) กลุ่มที่มีผู้ติดเชื้อ 2 คนมีจำนวน E[x = 2] = nP(x = 2) = 5000*28.8% = 1,440 กลุ่ม มีค่าความแปรปรวน V[x=2] = 5000*28.8%*71.2% = 1,025.28 กลุ่ม และส่วนเบี่ยงเบนมาตรฐาน 32.02 กลุ่ม

    (C3) กลุ่มที่มีผู้ติดเชื้อ 3 คนมีจำนวน E[x = 3] = nP(x = 3) = 5000*35.2% = 1,760 กลุ่ม มีค่าความแปรปรวน V[x=3] = 5000*35.2%*64.8% = 1,140.48 กลุ่ม และส่วนเบี่ยงเบนมาตรฐาน 33.77 กลุ่ม

การแจกแจงแบบปกติ

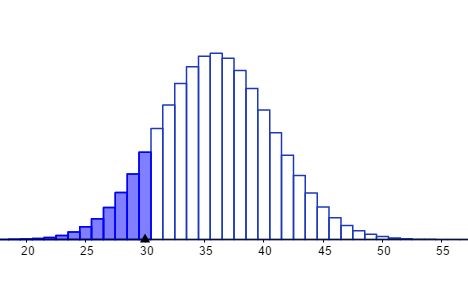
          ความน่าจะเป็นแบบทวินามนั้นเป็นความน่าจะเป็นแบบเต็มหน่วย (Discrete) ภาพที่ 4 เป็นภาพการแจกแจงทวินาม โดยส่วนแรเงาหมายถึงบริเวณที่มีค่าความน่าจะเป็นที่เกิดผลลัพธ์ไม่เกิน 30  P(x <= 30) โดยแท่งสี่เหลี่ยมแต่ละแท่งมีลักษณะเป็นมวลแทนค่าความน่าจะเป็น การวัดค่าความน่าจะเป็นการรวมฟังก์ชันมวลของความน่าจะเป็น (Probability Mass Functions)

ภาพที่ 4 การแจกแจงทวินาม

          ในขณะที่ภาพที่ 5 เป็นการแจกแจงความน่าจะเป็นในลักษณะต่อเนื่อง (Continuous) สามารถวัดค่าความน่าจะเป็นจากพื้นที่ใต้เส้นโค้งด้วยรวมฟังก์ชันความหนาแน่นของความน่าจะเป็น (Probability Density Functions) ด้วยวิธีการอินทิเกรต (Integration)

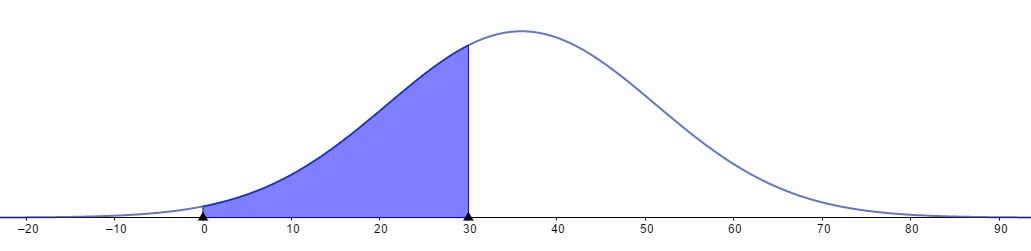
ภาพที่ 5 การแจกแจงปกติ

• การแจกแจงปกติ

          จากที่กล่าวมาข้างต้นว่าพื้นที่ใต้เส้นโค้งระฆังคว่ำคือความน่าจะเป็นนั้นหมายความว่า พื้นที่ทั้งหมดใต้เส้นโค้งจะต้องมีค่าเท่ากับ 1.00 หรือ 100 % โดยที่จุดสูงสุดของเส้นโค้งคือตำแหน่งของค่ากลาง (ความเฉลี่ย, ค่ามัธยฐาน, ฐานนิยม)  โดยมีส่วนเบี่ยงเบนมาตรฐานเป็นค่าแสดงการกระจายตัวออกจากค่ากลาง ถ้าเราให้ค่ากลางแทนด้วย M และส่วนเบี่ยงเบนมาตรฐานแทนด้วย SD แล้ว

          P( M – SD <= X <= M + SD) = 0.6826 นั้นคือพื้นที่ใต้เส้นโค้งช่วง [M - SD, M + SD] = 0.6826 ซึ่งคิดเป็น 68.26 % ของพื้นที่ทั้งหมดหมายความว่า มีข้อมูล 68.26 % อยู่รอบๆ ค่ากลาง

          P( M – 2SD <= X <= M + 2SD) = 0.9544 นั้นคือพื้นที่ใต้เส้นโค้งช่วง [M - 2SD, M + 2SD] = 0.9544 ซึ่งคิดเป็น 95.44 % ของพื้นที่ทั้งหมดหมายความว่า มีข้อมูล 95.44 % อยู่รอบๆ ค่ากลาง

          P( M – 3SD <= X <= M + 3SD) = 0.9973 นั้นคือพื้นที่ใต้เส้นโค้งช่วง [M - 3SD, M + 3SD] = 0.9973 ซึ่งคิดเป็น 99.73 % ของพื้นที่ทั้งหมดหมายความว่า มีข้อมูล 99.73 % อยู่รอบๆ ค่ากลาง

          สมมติให้ค่า alpha เป็นความน่าจะเป็นที่ X ไม่อยู่ในช่วง [a,b] แล้ว 1-alpha คือความน่าจะเป็นที่ X อยู่ในช่วง [a,b] ถ้าเรากำหนดให้ alpha = 0.5 จะได้ว่า 1 – alpha = 0.95 คือความน่าจะเป็นที่ X อยู่ในช่วง [a,b] เรียกช่วงนี้ว่าช่วงความเชื่อมั่น 95% แทนด้วย 95%[a,b] และเรียก alpha ว่าระดับนัยยะสำคัญ โดยที่

          P(x <= a) = alpha/2 และ P(x >= b) = alpha/2

          หรือ

          P(x <= a) = alpha/2 และ P(x <= b) = 1 - alpha/2

          อย่างไรก็ตามในกรณีที่ต้องการเปรียบเทียบข้อมูล 2 ชุด แน่นอนว่าข้อมูลแต่ละชุดอาจมีค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานที่แตกต่างกัน จึงควรทำให้อยู่ในมาตรวัดเดียวกันเรียกว่าการทำการแจกแจงแบบปกติให้เป็นมาตรฐาน (Standardize Normal Distribution) ด้วยค่า Z คำนวณได้จาก

          Z = (X – M)/SD

          ณ ตำแหน่ง X = M จะพบว่า Z = 0

          ณ ตำแหน่ง X = [M – 2SD, M + 2SD] จะพบว่า Z = [-2, 2] เป็นช่วง 95.44%

3.2 การวัดความเสี่ยง (Measuring Risk)

          ในการลงทุนหรือดำเนินกิจการใดก็แล้วแต่ล้วนมีความเสี่ยง ความเสี่ยงหมายถึงการได้รับผลประโยชน์ หรือผลตอบแทนไม่เป็นไปตามที่คาดหมาย ในกรณีเป็นการลงทุนเชิงธุรกิจผลตอบแทนเกิดจากส่วนต่างของการลงทุนและราคาขาย ราคาขายจึงเป็นสิ่งที่ไม่สามารถคาดเดาได้อย่างแม่นยำเช่นการลงทุนซื้อหุ้นที่มีราคาหน่วยละ 10 บาท คาดว่าจะขายได้ในราคา 17 บาท แต่เมื่อถึงเวลาจริงอาจพบว่าสามารถขายได้ในราคา 12 บาท

          ที่มาของความเสี่ยงนั้นอาจมาจากปัจจัยภายนอกในระดับมหภาคเช่นสภาวะเศรษฐกิจ ค่าเงิน อัตราแลกเปลี่ยน ภาษี สภาพอากาศ และการเมือง จัดเป็นความเสี่ยงที่เกิดจากระบบ (Systematic Risk) หรืออาจมาจากปัจจัยภายในเช่นการจัดการที่ไม่มีประสิทธิภาพมากพอ ศักยภาพในการแข่งขัน ทีมงานหรือคนงานที่ค่อย ๆลดคุณภาพลง จัดเป็นความเสี่ยงที่ไม่เป็นระบบ (Asset-Specific Risk) ส่งผลให้บริษัทมีรายได้ที่ไม่แน่นอนในอนาคตจากความเสี่ยงทางธุรกิจ (Business Risk) และอาจนำมาซึ่ง การกู้ยืม ระดมทุน ชำระหนี้ เกิดเป็นความเสี่ยงด้านการเงิน (Financial Risk)

           การวัดความเสี่ยงจะวัดจากอัตราผลตอบแทนในแต่ละช่วงเวลา O_t แตกต่างจากผลตอบแทนเฉลี่ย O_A ด้วยค่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน

          ความแปรปรวน S² = sum{ (O_t-O_A)² } / (n-1) เช่น ผลตอบแทนของการลงทุนในระยะ 10 ไตรมาสดังตารางที่ 3

 ตารางที่ 3 ผลตอบแทนการลงทุน 10 ไตรมาส

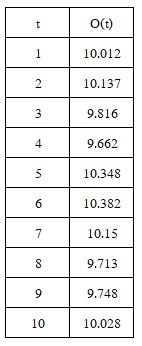
          พบว่ามีค่าเฉลี่ยหน่วยการลงทุนละ 9.9996 บาทและมีส่วนเบี่ยงเบนมาตรฐาน 0.26 บาท คิดเป็น 26 % หากต้องการวิเคราะห์หาโอกาสที่จะได้ผลตอบแทนจากการลงทุนหน่วยละ 10 บาทมากกว่า 5 % นั้นคือ ได้รับผลตอบแทนมากกว่า 10.5 บาท คำนวณได้จาก

          P( O > 10.5) = 1 - P( O <= 10.5) = 1 – 0.9737 = 0.0263 คิดเป็น 2.63 %

          ถ้าคิดในกรณีที่ไม่ขาดทุนจากการลงทุนนั้นคือได้รับผลตอบแทนไม่ต่ำกว่า 10 บาท

          P( O >= 10) = 1 – P(O < 10) = 1 – 0.5061 = 0.4939

          นั้นคือมีโอกาสที่จะได้กำไรจากการลงทุน 49.39%

          ในกรณีที่มีการตัดสินใจเลือกลงทุนอย่างน้อย 2 ธุรกิจเราสามารถวัดความเสี่ยงจากการลงทุนด้วยค่าสัมประสิทธิ์การแปรผัน (Coefficient of variation) เป็นการพิจารณาความเสี่ยงเทียบกับอัตราผลตอบแทน

          CV = S / O_A

          ตัวอย่างเช่นในการตัดสินใจเลือกลงทุนระหว่างกองทุน 1 และ กองทุน 2 เมื่อทำการวิเคราะห์รายละเอียดหลักทรัพย์ทั้งสองพบว่า

กองทุน 1 : ให้ผลตอบแทนเฉลี่ย 2.33% ส่วนเบี่ยงเบนมาตรฐาน 10.93%

กองทุน 2 : ให้ผลตอบแทนเฉลี่ย 2.93% ส่วนเบี่ยงเบนมาตรฐาน 10.51%

พิจารณา CV1 = 10.93% / 2.33% = 4.69 และ CV2 = 10.51% / 2.93% = 3.59 พบว่าภายใต้ผลตอบแทนที่เท่ากับกองทุน 2 มีความเสี่ยงต่ำกว่าจึงควรเลือกลงทุนในกองทุน 2

 ค่าประมาณเชิงปกติ

          จากภาพที่ 3 และภาพที่ 4 เราจะเห็นว่ารูปร่างของการกระจายตัวทั้งสองนั้นมีความคล้ายคลึงกัน ในเชิงปฏิบัติเราจึงสามารถใช้แทนกันได้นั้นหมายความว่า การแจกแจงเชิงปกติสามารถประมาณได้ด้วยการแจกแจงทวินาม ตัวอย่างเช่นในโรงงานผลิตสินค้าแห่งหนึ่ง พบว่าในการผลิตสิ้นค้าทุก ๆ 100 ชิ้นพบว่าจะมีสิ้นค้าประมาณ 2 ชิ้นที่มีตำหนิคิดเป็น 2 % ทางบริษัทต้องการหาว่าในการผลิตสิ้นค้า 5,000 ชิ้น จะมีจำนวนสินค้าที่มีตำหนิอยู่ในช่วงใด ในที่นี้ต้องการความเชื่อมั่นที่ 100 % แต่ในการแจกแจงแบบปกตินั้นเรารู้ว่า

          99.73%[a,b] = 99.73%[M – 3SD, M + 3SD]

          เราสามารถประมาณหาช่วงนี้ได้ด้วยการใช้การแจกแจงทวินามจะได้ M = 5000(0.02) = 100 ชิ้น และได้ส่วนเบี่ยงเบนมาตรฐาน S = sqrt (5000*0.02*0.98) = sqrt(98) = 9.9 จะได้ 99.73%[70.3, 129.7] นั้นคือจะมีชิ้นส่วนที่มีตำหนิอย่างน้อย 70.3 แต่ไม่เกิน 129.7 ชิ้น

           แนวคิดนี้ถูกนำไปใช้ประยุกต์ในการศึกษาการควบคุมคุณภาพ ซึ่งเป็นศาสตร์ที่มีความสำคัญมากในระดับอุตสาหกรรมการผลิต

• การควบคุมคุณภาพด้วยค่าเฉลี่ย

           การควบคุมคุณภาพนั้น จะใช้ค่าเฉลี่ยของ M  เป็นเส้นแบ่งแดน (Centerline) CL โดยที่ M เป็นค่าเฉลี่ยของตัวอย่าง และมีขอบเขตบนการควบคุม (Upper Control Limit) UCL และ ขอบเขตล่างการควบคุม (Lower Control Limit) LCL ด้วยเทคนิคการประมาณข้างต้นเราจะได้ว่า

            CL หมายถึงค่าเฉลี่ยของค่ากลางตัวอย่าง M(M)

            UCL(M) = M(M) – 3SD(M)

            LCL(M) = M(M) + 3SD(M) 

           คำนวณค่า SD(M) = M(R) / d₂(n)  โดยที่ M(R) หมายถึงค่าเฉลี่ยของพิสัย และ d₂(n) หมายถึงค่าคงที่ ASTM (American society for testing materials) ในกรณีที่สุ่มตัวอย่างมาตรวจสอบจำนวน n ชิ้น

          ตัวอย่างเช่นในการทำเกษตรต้องการตรวจสอบ และควบคุมคุณภาพผลผลิตที่ได้จากการปลูก จึงทำการสุ่มตรวจผลไม้ที่ได้จากการปลูก 5 แปลง แปลงละ 3 ผลพบว่า

                        แปลงที่ 1 ได้น้ำหนัก 0.97, 1.00 และ 0.98 กิโลกรัม

                        แปลงที่ 2 ได้น้ำหนัก 1.00, 1.20 และ 0.95 กิโลกรัม

                        แปลงที่ 3 ได้น้ำหนัก 0.95, 0.96 และ 1.00 กิโลกรัม

                      แปลง 4 ได้น้ำหนัก 1.00, 1.10 และ 0.97 กิโลกรัม

                      แปลง 5 ได้น้ำหนัก 0.99, 1.00 และ 1.10 กิโลกรัม

           เมื่อทำการวิเคราะห์รายละเอียดพบว่า ค่ากลางน้ำหนักในแต่ละรอบเท่ากับ 0.98, 1.05, 0.97, 1.02 และ 1.03 กิโลกรัมตามลำดับ และมีพิสัยแต่ละรอบเท่ากับ 0.03, 0.25, 0.05, 0.13 และ 0.11 กิโลกรัมตามลำดับ ดังตารางที่ 4

ตารางที่ 4 การวิเคราะห์รายละเอียดการสุ่มตรวจผลไม้จากแปลงปลูก 5 แปลง แปลงละ 3 ผล

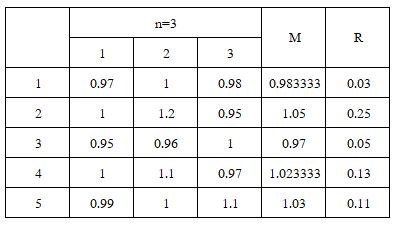
         พิจารณาค่าเฉลี่ยของค่ากลาง M(M) = 1.01 และ ค่ากลางของพิสัย M( R) = 0.11 ทำการสุ่มตัวอย่างมาสังเกต 3 ค่า (n=3) จะได้ค่า d2 = 0.17 จากตาราง ASTM พบว่า SD(M) = 0.07 จะได้ผังควบคุมประกอบด้วย เส้นควบคุม CL = 1.01, เส้นควบคุมขอบเขตบน UCL = 1.21 และ เส้นควบคุมขอบเขตล่าง LCL = 0.81 ดังภาพที่ 6

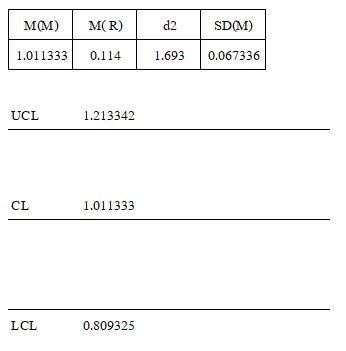
ภาพที่ 6 ผังควบคุมคุณภาพการสุ่มตรวจผลไม้ 3 ผลจากแปลงปลูก 5 แปลง

            4.2 การควบคุมคุณภาพด้วยค่า p

          ในกรณีที่ผลการสุ่มเป็นแบบทวิภาคในลักษณะผ่านหรือไม่ผ่าน มีตำหนิหรือไม่มีตำหนิ ถูกต้องหรือไม่ถูกต้อง เช่นโรงงานแห่งหนึ่งพบในการผลิตมีสินค้าที่มีตำหนิ 10 ชิ้นจากการสุ่มตรวจ 500 ชิ้น คิดเป็นสัดส่วน 10 / 500 หรือ 2.0% จะเห็นว่าเหตุการณ์ในลักษณะนี้เป็นความน่าจะเป็นแบบทวินาม หากเทียบกับปัญหาการควบคุมคุณภาพผลไม้ด้วยการแจกแจงแบบปกติข้างต้น ผนวกกับหัวข้อที่ได้ศึกษามาก่อนหน้านี้ ทำให้เราสามารถประมาณค่าการแจกแจงปกติดังกล่าวการแจกแจงแบบทวินาม

            สมมติให้ pi เป็นสัดส่วนของจำนวนค่าผิดพลาดจากการสุ่มตรวจครั้งที่ i ดังนั้น M(p) คือค่าเฉลี่ยของสัดส่วนที่ผิดพลาดในการควบคุมคุณภาพ

M(p) = (p1 + p2 + … + pn) / n

          เป็นเส้นควบคุม ส่วนเบี่ยงเบนมาตรฐานในกรณีที่เป็นการแจกแจงแบบทวินามจะได้ว่า

SD(p) = sqrt{ [M(p)*(1 - M(p))] / M(n) }  

          โดยที่ M(n) คือค่าเฉลี่ยของขนาดตัวอย่าง

           ตัวอย่างเช่นในการสุ่มตรวจการผลิตสินค้า 5 ครั้งพบว่า

          ผลิตครั้งที่ 1 จำนวน 400 ชิ้นมีของเสียจำนวน 10 ชิ้น

          ผลิตครั้งที่ 2 จำนวน 500 ชิ้นมีของเสียจำนวน 14 ชิ้น

          ผลิตครั้งที่ 3 จำนวน 450 ชิ้นมีของเสียจำนวน 14 ชิ้น

          ผลิตครั้งที่ 4 จำนวน 450 ชิ้นมีของเสียจำนวน   8 ชิ้น

          ผลิตครั้งที่ 5 จำนวน 500 ชิ้นมีของเสียจำนวน 10 ชิ้น

          จากตารางที่ 4 จะพบว่าสัดส่วนของเสียในการผลิตแต่ละครั้งเท่ากับ 2.5%, 2.8%, 3.1%, 1.7% และ 2% มีค่าเฉลี่ย M(p) = 2.4% จากการกลุ่มตัวอย่างเฉลี่ย M(n) = 460

ตารางที่ 4 ผลการสุ่มตรวจจำนวนของเสียจำนวน 5 ครั้ง

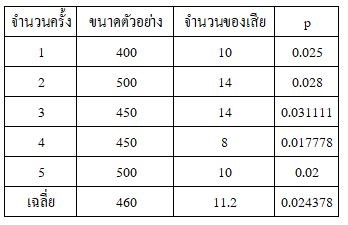
           เมื่อคำนวณค่าเส้นควบคุม CL = 0.024 เส้นควบคุมขอบเขตบน UCL =  0.046 และ เส้นควบคุมขอบเขตล่าง LCL = 0.003 ดังภาพที่ 7

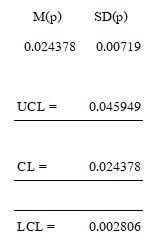
ภาพที่ 7 ผังควบคุมคุณภาพ

           แนวทางการตรวจสอบคุณภาพสินค้าจะทําขึ้นก่อนที่จะมีการส่งสินค้าไปยังผู้บริโภค หรือ ก่อนการวางจําหน่าย โดยทั่วไปแล้วผู้ผลิตมักจะเป็นฝ่ายตรวจสอบคุณภาพสินค้าที่ตนผลิต บางครั้งผู้รับสินค้าเองก็อาจทำการตรวจสอบคุณภาพสินค้าที่รับมา ก่อนดำเนินการผลิตหรือจัดจำหน่วยก็เป็นได้ ในทางปฏิบัติจะนิยมสุ่มเพียงบางส่วนเพื่อลดภาระค่าใช้จ่ายและเวลาในการตรวจสอบ จากนั้นจึงใช้การอนุมาน หากเป็นการสุ่มตัวอย่างเพื่อการยอมรับสินค้า จะมีเงื่อนไขจำนวนสินค้าบกพร่องมากสุดที่ยอมรับได้ใช้ประกอบการยอมรับหรือปฏิเสธสินค้าล๊อตนั้น ๆ แต่หากเป็นการตรวจสอบคุณภาพเพื่อปรับปรุงการผลิตแล้ว เมื่อไหร่ก็ตามมีค่าเฉลี่ยหลุดออกจากเส้นขอบเขตแล้วเป็นไปได้ว่าระบบการผลิตอาจมีปัญหาหรือมีข้อผิดพลาด นำไปสู่การวางแผนแก้ไขเพื่อให้การผลิตมีความเสถียรและมีประสิทธิภาพ

ความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล

          ในกรณีที่เรามีกลุ่มข้อมูล 2 กลุ่มโดยที่ค่าของข้อมูลกลุ่มที่ 1 ส่งผลกับค่าของข้อมูลกลุ่มที่ 2 เราสามารถอธิบายความสัมพันธ์หรือแนวโน้มของข้อมูล 2 กลุ่มนี้ได้โดยกำหนดให้ ข้อมูลกลุ่มแรกคือตัวแปรต้นหรือตัวแปรอิสระ (Independent Variables) และข้อมูลกลุ่มที่ 2 คือตัวแปรตาม (Dependent Variables) เราเรียกเซตของข้อมูลตัวแปรต้นว่า อินพุต (Inputs) และ เรียกเซตของตัวแปรตามว่าเอาท์พุต (Outputs) หากความสัมพันธ์ของอินพุตและเอาท์พุตมีรูปแบบ นิยามการทำงานได้ (Functional) แล้วเราสามารถออกแบบฟังก์ชันอธิบายการทำงานของระบบได้ดังภาพที่ 8

ภาพที่ 8 แผนผังแสดงระบบการทำงานแบบเป็นฟังก์ชัน 

• ความสัมพันธ์เชิงเส้น และไม่เป็นเชิงเส้น

          ในทางปฏิบัติเรานิยมอธิบายพฤติกรรมต่างๆในลักษณะเชิงเส้นเนื่องจากเป็นรูปแบบอย่างง่ายและมีความสะดวกในการคำนวณ อีกทั้งยังมีทฤษฎีทางคณิตศาสตร์เกี่ยวกับสมการเส้นตรงรองรับการวิเคราะห์และสังเคราะห์

            สมการเส้นตรงตัวแปรเดียว (linear equations in one variable) เขียนได้ในรูปของ y = ax + b หรือฟังก์ชันเชิงเส้น f(x) = ax + b เรียก a ว่าความชัน (slope) แสดงถึงแนวโน้มของข้อมูลที่มีการเพิ่มหรือลดสม่ำเสมอ หรือ มีลักษณะคงที่ก็ได้

            ถ้า a > 0 แล้วเอาท์พุตมีแนวโน้มเพิ่มขึ้นเมื่ออินพุตเพิ่ม

            ถ้า a < 0 แล้วเอาท์พุตมีแนวโน้มลดลงเมื่ออินพุตเพิ่ม

            ถ้า a = 0 แล้วเอาท์พุตคงที่

ส่วน ค่า b นั้นคือจุดตัดแกน y อาจหมายถึงค่าเริ่มต้นของระบบก็ได้

            สำหรับสมการไม่เป็นเชิงเส้น (nonlinear equations) หรือฟังก์ชันไม่เป็นเชิงเส้นอาจอยู่ในรูปของฟังก์ชันพหุนาม (polynomial functions)

          f(x) = a_nxⁿ + a_n-1x^n-1 + … + a₂x² + a₁x + a₀

           ฟังก์ชันเอกซ์โพเนนเชียล (exponential functions)

          f(x) = Ae^Bx

          ฟังก์ชันลอการิทึม (logarithm functions)

          f(x) = Aln(x) + B

           ซึ่งใช้อธิบายแนวโน้มข้อมูลที่มีลักเพิ่มขึ้นหรือลดลงไม่สม่ำเสมอ เช่นมีการเพิ่มอย่างช้าๆในช่วงแรกและเพิ่มขึ้นอย่างรวดเร็วในช่วงปลาย (slow growth) หรือ ลดลงอย่างรวดเร็วในช่วงแรกแต่ช้าลงในช่วงปลาย (rapid decay) เป็นต้น

          ฟังก์ชันตรีโกณมิติ (sinusoidal functions)

          f(x) = Asin(wt + p)

          ใช้อธิบายคลื่น การสั่นสะเทือน การกวัดแกว่งของระบบ                  

           ฟังก์ชันลอจิสติก (Logistic functions)

           f(x) = A / (1 + e^{-(x + B)})

          ใช้อธิบายพฤติกรรมระบบที่มีการเพิ่มขึ้นอย่างรวดเร็วในช่วงกลาง

• ตัวอย่างความสัมพันธ์เชิงฟังก์ชันระหว่างข้อมูล

           พิจารณาปริมาณน้ำฝนในจังหวัดกาญจนบุรีในปี พ.ศ. 2558 ในตารางที่ 5

ตารางที่ 5 ปริมาณน้ำฝนของจังหวัดกาญจนบุรีปี พ.ศ. 2558

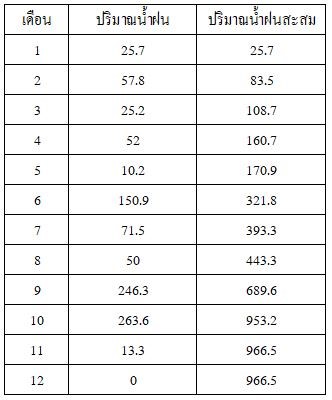
           หากเราน้ำข้อมูลที่ในตารางที่ 5 มาพิจารณาความสัมพันธ์ระหว่างปริมาณน้ำฝนในแต่ละเดือนจะได้กราฟข้อมูลที่มีลักษณะดังภาพที่ 9

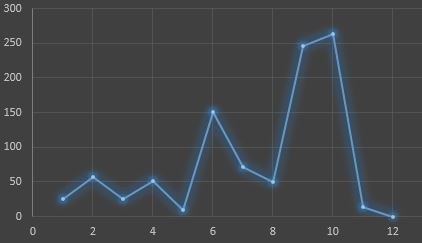
ภาพที่ 9 ประมาณน้ำฝนแต่ละเดือนของจังหวัดกาญจนบุรีในปีพ.ศ. 2558

           จากภาพที่ 9 จะเห็นว่าเส้นกราฟมีลักษณะเป็นรูปสามเหลี่ยมสามารถแบ่งได้เป็น 4 ช่วง การจะหาเส้นแนวโน้มหรือฟังก์ชันเพื่อพยากรณ์ปริมาณน้ำฝนในแต่ละเดือนเป็นไปได้ยาก ทำให้การพยากรณ์ดังกล่าวต้องใช้อนุกรมเวลา (time series) ซึ่งจะไม่กล่าวถึงในที่นี้ อย่างไรก็ตามหากเราพิจารณาถึงปริมาณน้ำฝนสะสมตลอดปีพ.ศ. 2558 จะได้เส้นแนวโน้มดังภาพที่ 10

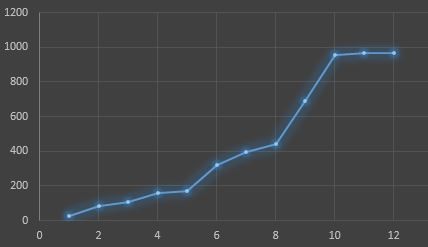
ภาพที่ 10 ปริมาณน้ำฝนสะสมของจังหวัดกาญจนบุรีในปี พ.ศ. 2558

           ในภาพที่ 10 นี้เราสามารถสร้างฟังก์ชันปรับเรียบเพื่อหาสมการทำนายปริมาณน้ำในจังหวัดกาญจนบุรีจากข้อมูลปริมาณน้ำฝนสะสมในปีพ.ศ. 2558 ได้

           ในการเลือกฟังก์ชันเพื่อสร้างเส้นตรง หรือเส้นโค้งเรียบ นั้นขึ้นกับพฤติกรรมข้อมูล จากภาพที่ 10 เราสามารถวิเคราะห์และคาดการณ์ภายใต้สมมติฐานที่ไม่คำนึงถึงการศูนย์เสียน้ำได้ว่า

          C1: ปริมาณน้ำฝนสะสมมีการเพิ่มขึ้นคงที่สอดคล้องกับฟังก์ชันเส้นตรง

          C2: ปริมาณน้ำฝนมีน้อยในช่วงต้นปีแต่จะมีมากในช่วงปลายปีสอดคล้องกับฟังก์ชันเอกซ์โพเนนเชียล

          C3: ปริมาณน้ำฝนจะเพิ่มขึ้นอย่างรวดเร็วในช่วงกลางปีสอดคล้องกับฟังก์ชันลอจิสติก

          เมื่อใช้วิธีการถดถอยเชิงเส้น เราสามารถหารูปแบบฟังก์ชันที่ใช้พยากรณ์ปริมาณน้ำฝนสะสมได้ โดยใช้ค่าคาดเคลื่อน SSE และ R² ประกอบการตัดสินใจเลือกใช้ฟังก์ชัน ได้ผลดังนี้

            C1: ฟังก์ชันเส้นตรงจะอยู่ในรูป

f(x) = 96.99x – 190.16, (SSE = 109,819, R² = 0.92)

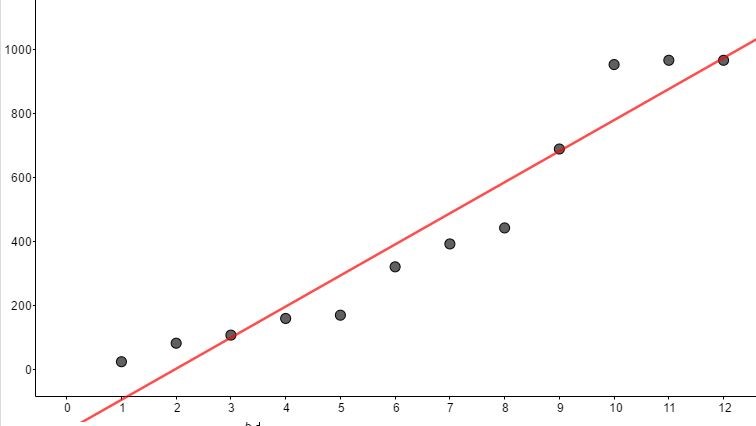
ภาพที่ 11 เส้นแนวโน้มของฟังก์ชันเส้นตรง

          C2: ฟังก์ชันเอกซ์โพเนนเชียลจะอยู่ในรูป

f(x) = 38.18e^0.31x, (SSE = 344,331 R² = 0.76)

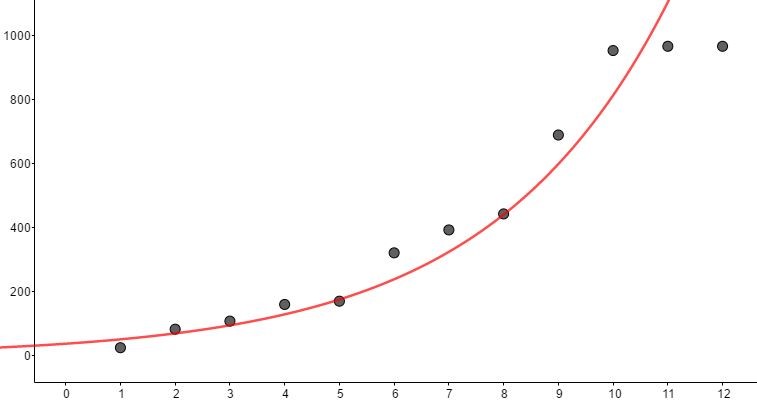
ภาพที่ 12 เส้นแนวโน้มของฟังก์ชันเอกซ์โพเนนเชียล

          C3: ฟังก์ชันลอจิสติกจะอยู่ในรูป

f(x) =1201.22 / (1 + 61.36e^-0.49x), (SSE = 35,478 R² = 0.9756)

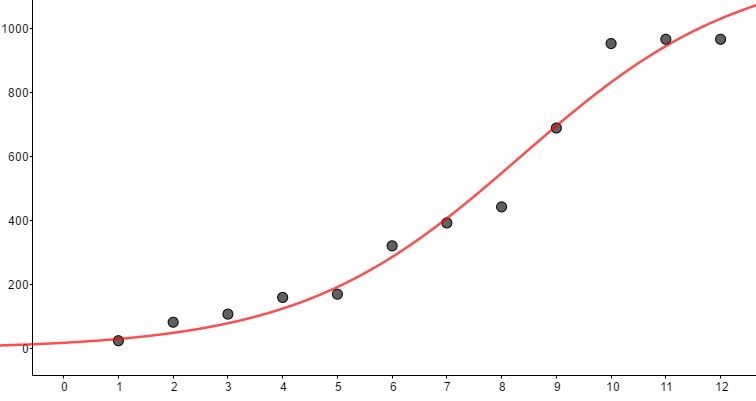
ภาพที่ 13 เส้นแนวโน้มของฟังก์ชันลอจิสติก

          จะเห็นได้ว่าฟังก์ชันลอจิกติก (C3) นั้นมีค่าคลาดเคลื่อนกำลังสองสะสมน้อยสุด และมีค่า R² ที่แสดงถึงความเข้ากันได้กับข้อมูลสูงที่สุดสังเกตได้จากระหว่างห่างระหว่างจุดและเส้นโค้งในภาพที่ 11, 12 และ 13 อย่างไรก็ตามพฤติกรรมต่าง ๆในธรรมชาตินั้นไม่ได้มีลักษณะเป็นเชิงเส้น ในภาพที่ 14 จะเห็นว่าพหุนามกำลัง 9 นั้นให้ฟังก์ชันพยากรณ์ที่ดีกว่าเส้น C1, C2 และ C3 แต่การใช้งานนั้นมีความยุ่งยากซับซ้อนในการคำนวณ ซึ่งหากพูดถึงความสะดวกในการใช้งานภายใต้ความคลาดเคลื่อนที่ยอมรับได้แล้วฟังก์ชันเส้นตรงย่อมเป็นตัวเลือกที่ดีที่สุด เราจะศึกษาวิธีการประมาณเชิงเส้นในหัวข้อถัดไปเพื่อให้เกิดค่าความคลาดเคลื่อนน้อยที่สุดเรียกเทคนิคนี้ว่า least square

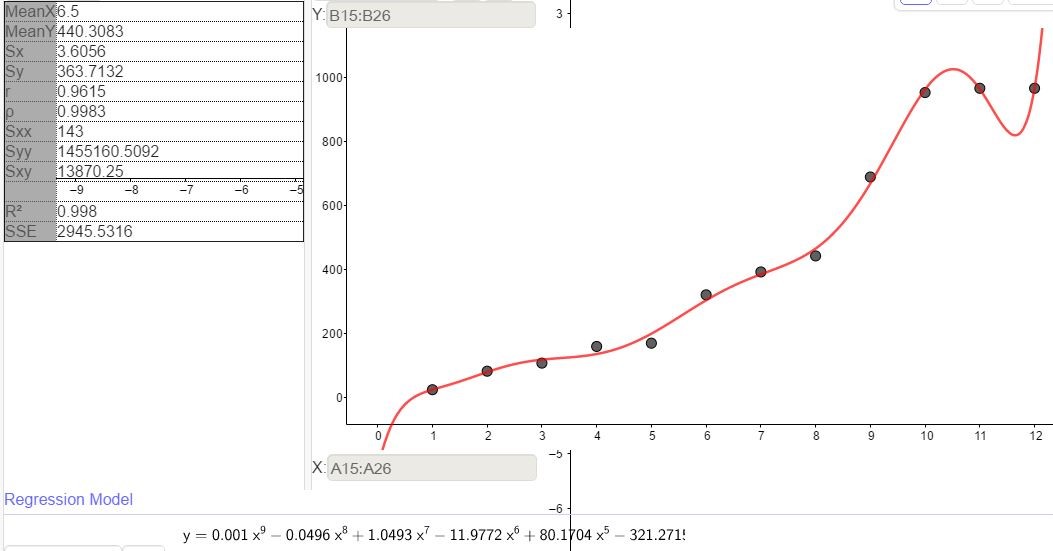
ภาพที่ 14 ฟังก์ชันพหุนามกำลัง 9 (SSE = 2945.53, R² = 0.998)

ตัวแบบเชิงเส้น

          สมการเส้นตรงและการประมาณเชิงเส้น

          ในการเก็บข้อมูลเพื่อศึกษาพฤติกรรม หรือความสัมพันธ์ระหว่างข้อมูล เราจะได้เซตข้อมูล จำนวนมาก ในกรณีที่เรามีชุดข้อมูล 2 ชุดที่มีความสัมพันธ์กันในรูป {(xi, yi), I = 1, 2, 3, …, n } ซึ่งมีลักษณะเป็นข้อมูลแบบเต็มหน่วย (discrete) แต่เราต้องการฟังก์ชัน หรือ สร้างสมการอธิบายความสัมพันธ์ ด้วยข้อมูลที่มีอยู่เป็นจำนวนมาก เราสามารถวิเคราะห์รายละเอียดของข้อมูลด้วยค่าคาดหมาย E[x] จะหมายถึงค่าเฉลี่ย และ V[x] หมายถึงความแปรปรวน มีคุณสมบัติดังนี้

          ถ้าพิจารณาค่า E[xi + yi] = sum[xi + yi] / n = sum[xi] / n + sum[yi] / n = E[xi] + E[yi]

          (P1)  E[xi + yi] = E[xi] + E[yi]           

          พิจารณาค่าคาดหมายของค่าคงที่ E[ c ] = nc/n = c

          (P2) E[c] = c

          พิจารณา V[xi] = E[(xi – E[xi])²] = E[(xi)² -2(xi)E[xi] + E²[xi] = E[(xi)²] - 2E²[xi] + E²[xi]

            (P3)  V[xi] = E[(xi)²] – E²[(xi)]

          พิจารณา COV[(xi)(yi)] = E[(xi – E[xi])(yi – E[yi])]  จะได้

          COV[(xi)(yi)] = E[(xi)(yi)] - E[(xi)E[yi]] – E[E[xi](yi)] + E[xi]E[yi]

          ดังนั้น

          (P4)  COV[(xi)(yi)] = E[(xi)(yi)] – E(xi)E(yi)

          สังเกตว่า COV[(xi)(xi)] = V[xi]

          ดังที่กล่าวมาข้างต้นว่า ถ้าเราสามารถสร้างในรูปแบบของสมการเส้นตรงได้ นั้นคือ พฤติกรรมหรือความสัมพันธ์ข้อมูลมีลักษณะเป็นเชิงเส้น เราจะได้สมการในรูป  y = Ax + B เรียกว่าตัวแบบเชิงเส้น (Linear models) เป้าหมายสำคัญคือเราต้องการสมการที่อธิบายจุดของข้อมูลได้ทุกจุด แต่ในความเป็นจริงเส้นตรงดังกล่าวย่อมไม่ผ่านจุดข้อมูลทุกจุด เราทำได้เพียงการหาเส้นตรงที่อยู่ใกล้กับจุดทุกจุดให้มากที่สุด นำมาซึ่งแนวคิดของการหาค่าต่ำสุดนั้นเอง

            เราพิจารณาระยะห่างระหว่างจุด (xi,yi) กับเส้นตรง y = Ax + B ซึ่งเป็นค่าความคลาดเคลื่อนวัดได้จาก

          (ei)² = (yi – y)² = (yi - Axi+B)² = (yi)² – 2(yi)[Axi - B) + (Axi + B)²

          ได้

          (ei)² = (yi – y)² = (yi - Axi+B)² = (yi)² - 2A(xi)(yi) - 2B(yi) + A²(xi)² + 2AB(xi) + B²

          พิจารณาค่าคาดหมายจากคุณสมบัติ

          E[(ei)²] =  E[(yi)²] – E[2A(xi)(yi)] + E[2B(yi)] + E[A²(xi)²] + E[2AB(xi)] + E[B²]

           จากคุณสมบัติข้อ (P1) และ P(2) จะได้

          E[(ei)²] = E[(yi)]² – 2AE[(xi)(yi)] - 2BE[yi] + A²E[(xi)²] + 2ABE[xi] + B²

          เพื่อความสะดวกในการเขียนเราจะแทนด้วยสัญลักษณ์ดังนี้

          E[e²] = E[x²] A² + B² + 2ABE[x] – 2E[x,y]A – 2E[y]B + E[y²]

          เนื่องจากในขั้นตอนการวิเคราะห์รายละเอียดข้อมูลเราจะได้ค่า E(x), E(y), V(x), และ V(y) จึงใช้คุณสมบัติ (P2) แทนค่า E[x²] และ E[y²] จะได้ และ E[x,y] ใน (P4)

         E[e²] = (V[x] + E²[x])A² + B² + 2ABE[x] – 2(COV[x,y] + E[x]E[y])A – 2E[y]B + V[y] + E²[y]

          จะเห็นว่ามีตัวแปรไม่ทราบค่าคือ A และ B กำหนดให้ F เป็นฟังก์ชันของ A และ B จะได้ว่า

          F(A,B) = (V[x] + E²[x])A² + B² + 2ABE[x] – 2(COV[x,y] + E[x]E[y])A – 2E[y]B + V[y] + E²[y]

          ในการหาค่าต่ำสุด เราจะให้วิชาแคลคูลัสในการหาค่าวิกฤตโดยกำหนดให้ A เป็นตัวแปรและ B เป็นคงที่ จากนั้น กำหนดให้ B เป็นตัวแปรและ A เป็นค่าคงที่ จะได้อนุพันธ์  2 ค่าคือ

          D_AF(A,B) =  2(V[x] + E²[x])A + 2BE[x] – 2(COV[x,y] + E[x]E[y])

          และ

          D_B(A,B) = 2B + 2AE[x] – 2E[y]

กำหนดให้อนุพันธ์มีค่าเท่ากับศูนย์จะได้ระบบสมการต่อไปนี้

          COV[x,y] + E[x]E[y] = (V[x] + E²[x])A + E[x]B

          E[y] = E[x]A + B

          แทนค่า B = E[y] – E[x]A จะได้

          COV[x,y] + E[x]E[y] = (V[x] + E²[x] – E[x]E[x])A  + E[x]E[y]

          COV[x,y] = (V[x])A

         จะได้ความชันเท่ากับ

         A = COV[x,y] / (V[x])

         และจุดตัดแกน y คือ

         B = E[y] – E[x]A

• ตัวอย่างการประยุกต์ใช้ตัวแบบเชิงเส้น

จากข้อมูลอัตราการตายจากโรคมะเร็งปอดและหลอดลมของจังหวัดกาญจนบุรีตั้งแต่ปี พ.ศ. 2556 – 2561 แสดงได้ดังตารางที่ 6

ตารางที่ 6 อัตราตายด้วยโรคมะเร็งชนิดต่างของจังหวัดกาญจนบุรี ปี 2556-2560

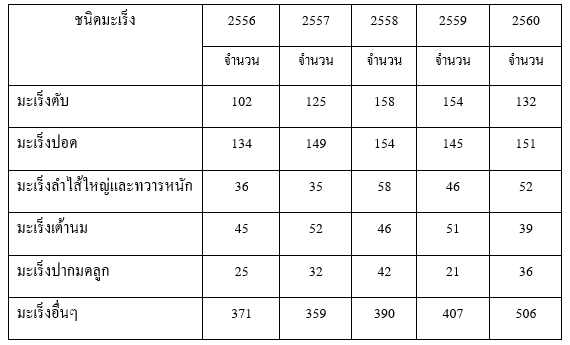
ที่มา : กองยุทธศาสตร์และแผนงาน กระทรวงสาธารณสุข (อ้างอิงจากกรมการปกครองกระทรวงมหาดไทย)

          จากตารางที่ 6 เราสามารถคำนวณค่า E คือค่าเฉลี่ยของมะเร็งแต่ละชนิดผลว่าในแต่ละปีจะมีผู้เสียชีวิตด้วยมะเร็งชนิดต่าง ๆโดยที่มะเร็งปอดเสียชีวิตมากสุดที่ 147 คนต่อปี รองลงมาคือมะเร็งตับ 135 คนต่อปี และมะเร็งปากมดลูกเสียชีวิตน้อยสุดเฉลี่ยปีละ 32 คน

          เมื่อพิจารณาถึงค่า A ในตารางที่ 7 ที่ซึ่งคือความชันของเส้นตรง หมายถึงอัตราการตายที่เพิ่มขึ้น/ลดลงตลอดระยะเวลา   5 ปี พบว่า มะเร็งตับมีอัตราการตายเพิ่มขึ้นสูงเป็นอันดับที่ 1 ในอัตรา 9 คนต่อปี รองลงมาคือมะเร็งลำไส้ใหญ่และทวารในอัตรา 5 คนต่อปี และมะเร็งปากมดลูกที่อัตราการตายเพิ่มขึ้นน้อยที่สุดที่ 2 คนต่อปี อย่างไรก็ตามจะเห็นได้ว่ามะเร็งเต้านมกลับมาอัตราการตายที่ลดลงปีละ 2 คน และเราจะได้สมการทำนายจำนวนผู้ป่วยเป็นมะเร็งในปีถัดไปได้จากสมการ y = Ax + B

          มะเร็งตับ                                                           y = 8.9x + 116.4

          มะเร็งปอด                                                         y = 3x + 140.6

          มะเร็งลำไส้ใหญ่และทวารหนัก                             y = 4.3x + 36.8

          มะเร็งเต้านม                                                      y = -1.3x + 49.2

          มะเร็งปากมดลูก                                                 y = 1.1x + 29

ตารางที่ 7 รายละเอียดข้อมูลค่าเฉลี่ย ค่าความแปรปรวน แนวโน้ม และสถานะเริ่มต้นของมะเร็งชนิดต่างๆ 

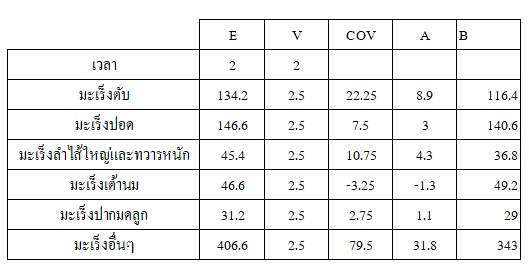
          เมื่อนำสมการข้างต้นไปใช้จะได้ค่าในตารางที่ 8 เมื่อนำไปเปรียบเทียบกับข้อมูลเดิมจะได้ค่าความคลาดเคลื่อนในตารางที่ 9

ตารางที่ 8 ค่าประมาณผู้ป่วยมะเร็งชนิดต่าง ๆด้วยการประมาณเชิงเส้น

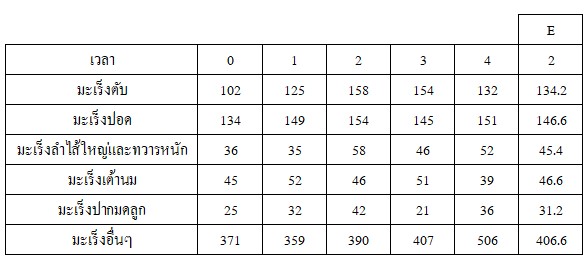
ตารางที่ 9 ค่าความคลาดเคลื่อนการประมาณค่าด้วยการประมาณเชิงเส้น

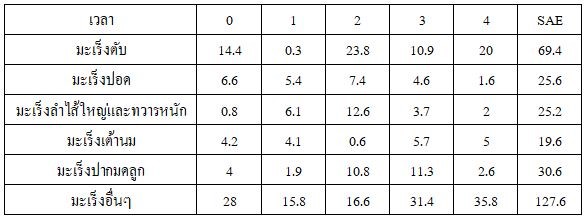
          จะเห็นได้ว่า การประมาณค่ามีค่าความคลาดเคลื่อนสมบูรณ์ทั้งสิ้น 127.6  ยังถือว่าไม่ใช่ตัวแบบหรือตัวประมาณที่ดีนัก อาจเป็นไปได้ว่าพฤติกรรมอาจไม่มีแนวโน้มเป็นเชิงเส้น ซึ่งมีวิธีการวิเคราะห์ค่าความเป็นเชิงเส้น ร่วมถึงการวิเคราะห์การเข้ากันได้ของสมการกับข้อมูลซื่งไม่ได้กล่าวไว้ ณ ที่นี้ นอกจากนี้ยังอาจเป็นไปได้ว่าข้อมูลที่เรามีอยู่น้อยเกินไป ไม่มีความถูกต้องและมากพอที่จะทำให้การพยากรณ์มีความแม่นยำ อย่างไรก็ตามการหากเราต้องการเพียงศึกษาพฤติกรรมและดูแนวโน้มแล้ว แนวทางดังกล่าวก็เพียงพอสำหรับการประกอบการตัดสินใจการวางแผนและพัฒนารับมือกับปัญหาได้

แหล่งที่มา

Harnett, D.L., Horrell, J.F. (1998). Data, Statistics and decision model with Excel. John Wiley & Sons. USA.

Dancey, C.P., Dancey, Reidy, J. (2011). Statistics without maths for psychology. Pearson. USA.

ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง

วีระ ยุคุณธร (2020) เอกสารประกอบการอบรม การแก้ปัญหาเชิงคำนวณด้วยไพธอน มหาวิทยาลัยราชภัฏกาญจนบุรี.

แผนพัฒนาจังหวัดกาญจนบุรี 4 ปี (พ.ศ. 2561 – 2564)

แผนพัฒนาจังหวัดกาญจนบุรี 4 ปี (พ.ศ. 2557 – 2560)