เรขาคณิตขั้นสูงระดับมัธยมปลาย
การวัดในระนาบ
คำศัพท์ Geo หมายถึงการวัดในระบบโลก ในการศึกษาขั้นต้นจึงเป็นการวัดด้าน มุม พื้นที่ และปริมาตร จุดกำเนิดของวิชาเรขาคณิตนั้นไม่เป็นที่ทราบแน่ชัด แต่การศึกษาเรขาคณิตอย่างเป็นระบบ นับเป็นระบบแรกๆของโลกคือเรขาคณิตระบบยูคลิดภายใต้ชื่อหนังสือ อิลิเมนต์ ที่ได้รับความนิยมและมีอิทธิพลต่อแนวคิดแบบวิทยาศาสตร์อย่างมากในสมัยนั้น แม้ว่าในยุคแรก ๆนั้น หนังสือเล่มนี้อาจมีข้อบกพร่องตามหลักการคณิตศาสตร์ในยุคปัจจุบันอยู่บ้าง แต่ได้มีนักคณิตศาสตร์ที่ปรับปรุงและพัฒนาให้มีความรัดกุมซึ่ง สาระสำคัญของหนังสืออิลิเมนต์สรุปได้ดังนี้

ภาพที่ 1 รูปทรงเรขาคณิตทางคณิตศาสตร์
ที่มา https://pixabay.com/ , geralt
เล่มที่ 1 ว่าด้วยการให้นิยามศัพท์ และสัจพจน์ทางเรขาคณิต เล่มที่ 2 เป็นแนวคิดของพิธาโกรัส
เล่มที่ 3 เป็นการวัดเกี่ยวกับวงกลม เล่มที่ 4 รูปหลายเหลี่ยม เล่มที่ 5 ทฤษฎีบทสัดส่วน
เล่มที่ 6 ทฤษฎีบทสัดส่วนกับเรขาคณิตในระนาบ เล่มที่ 7 สมบัติของตัวเลขและขั้นตอนวิธีของยูคลิด
เล่มที่ 8 สัดส่วนต่อเนื่องและอนุกรมเรขาคณิต เล่มที่ 9 ทฤษฎีจำนวนเบื้องต้น
เล่มที่ 10 จำนวนอตรรกยะ เล่มที่ 11 เส้นและระนาบในปริภูมิ เล่มที่ 12 ปริมาตร
เล่มที่ 13 รูปทรงเรขาคณิตชนิดต่าง ๆ
ในที่นี้เราจะยกตัวอย่างข้อค้นพบสำคัญบางประการ
ข้อค้นพบของทาเลส
-
วงกลมถูกแบ่งครึ่งด้วยเส้นผ่านศูนย์กลาง
-
มุมที่ฐานของสามเหลี่ยมหน้าจั่วย่อมเท่ากัน
-
มุมตรงข้ามที่เกิดจากเส้นตรงสองเส้นตัดกันมีขนาดเท่ากัน
-
สามเหลี่ยมที่มีมุมเท่ากับสองมุม และด้านที่อยู่ระหว่างมุมทั้งสองเท่ากันด้วย สามเหลี่ยมนั้นจะเท่ากันทุกประการ
-
มุมในครึ่งวงกลมเป็นมุมฉาก
ผลงานของพิธาโกรัส
1.เส้นขนาดกับมุมภายในของรูปสามเหลี่ยม
ประพจน์ที่ 1 มุมภายในของรูปสามเหลี่ยมมีค่าเท่ากับ 180 องศา
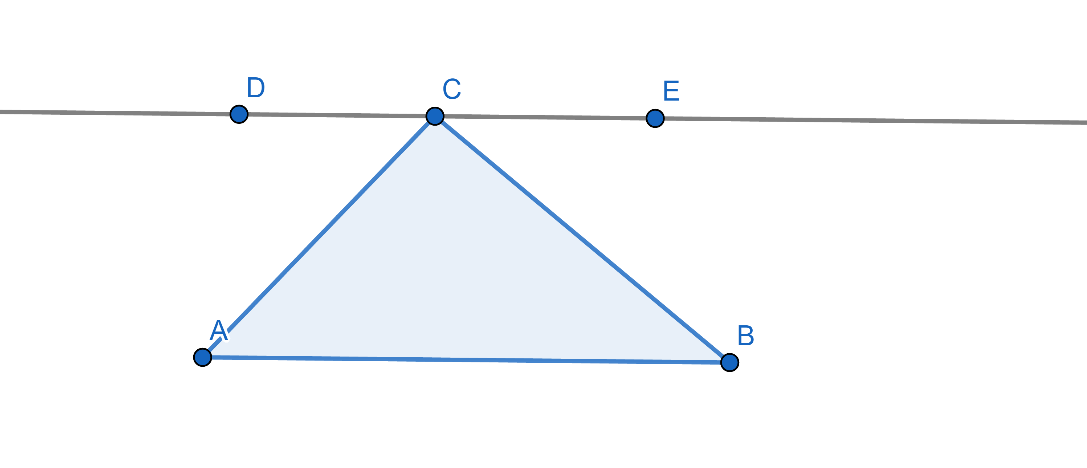
ภาพที่ 2 ภาพประกอบการพิสูจน์ประพจน์ที่ 1
ขั้นตอนที่ 1 สร้าง สามเหลี่ยมABC
ขั้นตอนที่ 2 ลากเส้นขนานกับ ด้านAB และผ่าน จุดC
ขั้นตอนที่ 3 กำหนด จุดD และ จุดE โดยมี จุดC อยู่ระหว่างจุดทั้งสอง
ขั้นตอนที่ 4 จะเห็นว่า มุมDCA = มุมCAB และ มุมBCE = มุมCBA เนื่องจากเป็นมุมแย้ง
ขั้นตอนที่ 5 มุมDCA + มุมACB + มุมBCE = 180 องศา เนื่องจากเป็นมุมบนเส้นตรง
ขั้นตอนที่ 6 แทนค่ามุมที่เท่ากันในขั้นตอนที่ 4 ได้ มุมCAB + มุมACB + มุมCBA = 180 องศา ซึ่งเป็นมุมภายในของรูปสามเหลี่ยม
สรุปได้ว่ามุมภายในของรูปสามเหลี่ยมมีค่าเท่ากับ 180 องศา
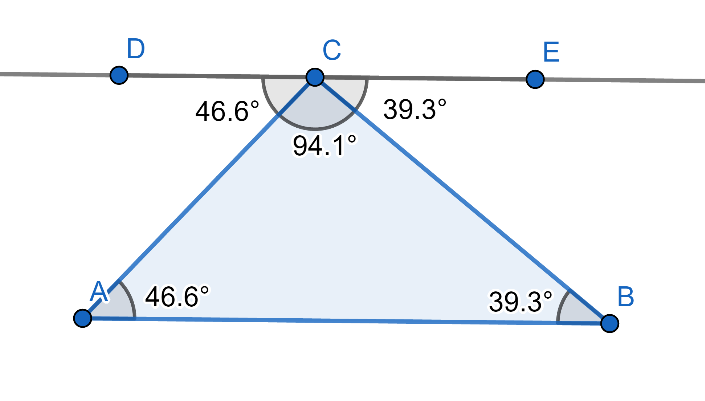
ภาพที่ 3 ตัวอย่างประกอบประพจน์ที่ 1
ประพจน์ที่ 2 สามเหลี่ยมABC เป็นสามเหลี่ยมมุมฉาก (มุมฺB เป็นมุมฉาก) ก็ต่อเมื่อ AC2 = AB2 + BC2ตัวอย่างเช่นในภาพที่ 4
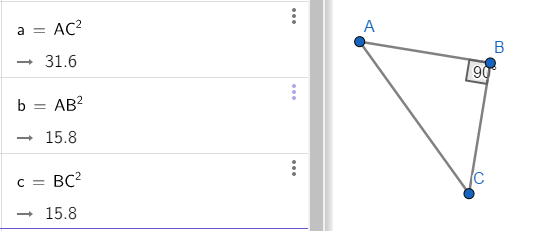
ภาพที่ 4 สามเหลี่ยมมุมฉาก ABC สอดคล้องกับสมการ AC2 = AB2 + BC2
กำหนดให้ สามเหลี่ยมABC เป็นสามเหลี่ยมมุมฉาก จะเห็นได้ว่า AC2 = AB2 + BC2 --> 31.6 = 15.8 + 15.8
สมการดังกล่าวเป็นจริง ในทางกลับกันดังภาพที่ 5 กำหนดเลขสามคำนวณคือ 12, 35 และ 37 จะตรวจสอบว่า 372 = 352 – 122 หรือไม่พิจารณา 372 – 352 = (37 – 35)(37 + 35) = 2(64) = 122 เราสรุปได้ว่าเลขชุดนี้สอดคล้องกับความยาวด้านของรูปสามเหลี่ยมมุมฉาก
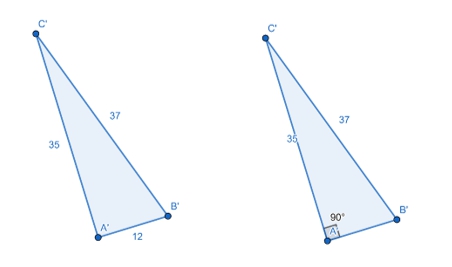
ภาพที่ 5 สามเหลี่ยมที่มีด้านยาว 12, 35 และ 37 เป็นสามเหลี่ยมมุมฉาก
ต่อไปเราจะทำการวางนัยยะทั่วไปกำหนดให้สามเหลี่ยมมุมฉากมีด้านประกอบมุมฉากยาว a หน่วย และ b หน่วย และมีด้านตรงข้ามมุมฉากยาว c หน่วย จำนวนสามจำนวนนี้ (a ,b, c) จะสอดคล้องกับสมการ c2 = a2 + b2
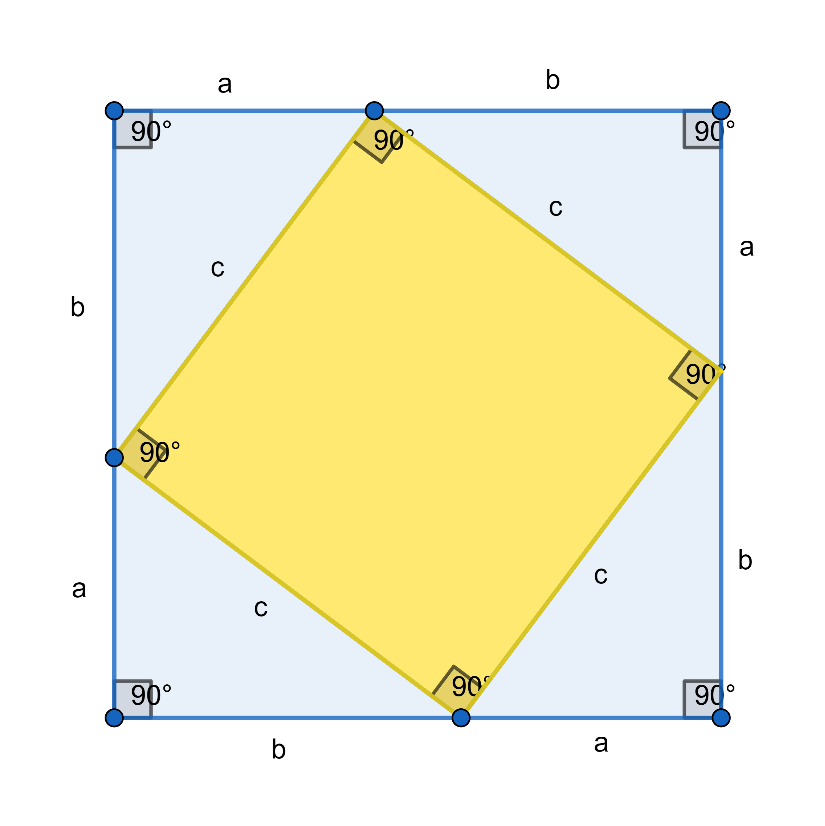
ภาพที่ 6 ภาพประกอบการพิสูจน์ทฤษฎีบทพิธาโกรัส
จากภาพที่ 6 จำแนกรูปเรขาคณิตได้ดังนี้
สามเหลี่ยมมุมฉากที่เท่ากับทุกประการจำนวน 4 รูป
สี่เหลี่ยมที่มีขนาด c x c จำนวน 1 รูป
สี่เหลี่ยมที่มีขนาด (a + b) x (a + b) จำนวน 1 รูป
สังเกตว่า ผลรวมของพื้นที่รูปสามเหลี่ยม 4 รูป และรุปสี่เหลี่ยมขนาด c x c มีค่าเท่ากับพื้นที่ของรูปสี่เหลี่ยมขนาด (a + b) x (a + b) เขียนเป็นสมการได้ดังนี้
4[ab /2] + c2 = (a + b)2
2ab + c2 = a2 + 2ab + b2
c2 = a2 + b2
ประพจน์ที่ 3 สามเหลี่ยม ABC คล้ายกับสามเหลี่ยม AB’C’ ก็ต่อเมื่อ AB/AB’ = BC/B’C’ = AC/AC’
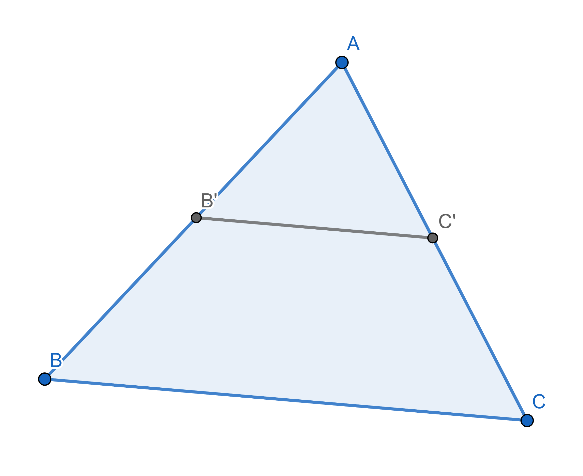
ภาพที่ 7 ภาพประกอบประพจน์ที่ 3
สร้าง ส่วนของเส้นตรงBC’ พิจารณาสัดส่วน AB’ / AB จากนั้น คูณด้วย h/2 ทั้งเศษและส่วน จะได้
AB’ / AB = [(h x AB’) / 2] / [(h x AB) / 2 ] = พื้นที่ AB’C’ / พื้นที่ ABC’
ดังภาพที่ 8 ในทำนองเดียวกันดังภาพที่ 9 จะพบว่า AC’ / AC = [(h x AC’) / 2] / [(h x AC) / 2 ] = พื้นที่ AB’C’ / พื้นที่ AB’C
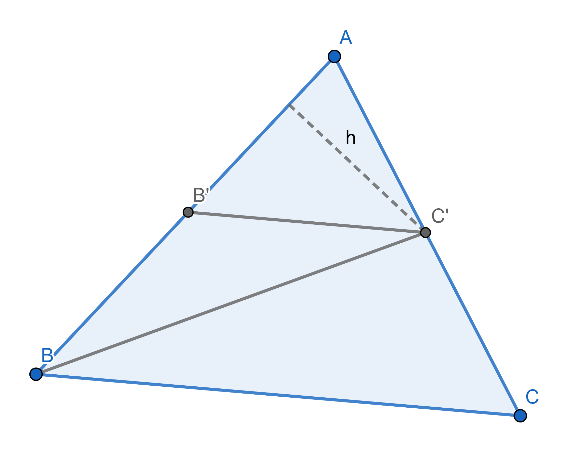
ภาพที่ 8 ภาพประกอบการพิจารณาประพจน์ที่ 3
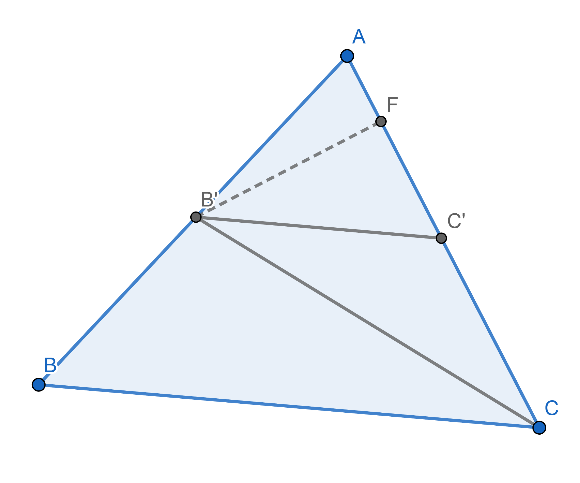
ภาพที่ 9 ภาพประกอบการพิจารณาประพจน์ที่ 3
เนื่องจาก สามเหลี่ยมBB’C’ และสามเหลี่ยม CC’B’ ใช้ฐาน B’C’ ร่วมกันจากการสร้าง B’C’ ให้ขนานกับ BC ทำให้พื้นที่สามเหลี่ยมBB’C’ = พื้นที่สามเหลี่ยม CC’B’ ส่งผลให้ พื้นที่ ABC’ = พื้นที่ AB’C ดังนั้น
AB’ / AB = พื้นที่ AB’C’ / พื้นที่ ABC’ = พื้นที่ AB’C’ / พื้นที่ AB’C = AC’ / AC
สามารถทำได้ในทำนองเดียวกันว่า AB/AB’ = BC/B’C’
ในทางกลับกัน เราให้ สามเหลี่ยม ABC คล้ายกันกับ สามเหลี่ยม AB’C’’ สมมติให้ สามเหลี่ยม ABC’ เป็นสามเหลี่ยม ดังภาพที่ 10 ซึ่งมีสัดส่วน AB’/ AB = AC’ / AC
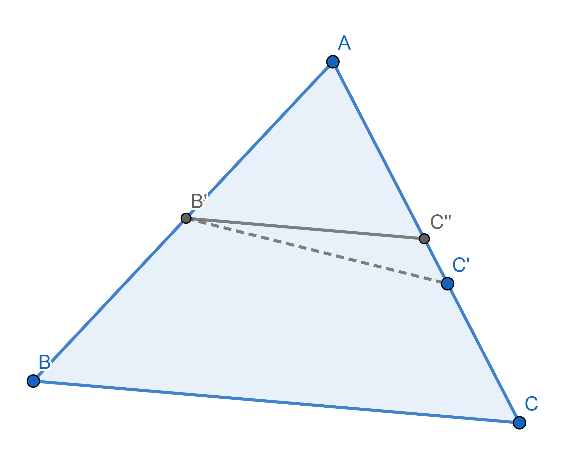
ภาพที่ 10 ภาพประกอบการพิจารณาขากลับของประพจน์ที่ 3
เนื่องจาก สามเหลี่ยม ABC คล้ายกันกับ สามเหลี่ยม AB’C’’ จะได้ว่า AB / AB’ = AC / AC’’ สังเกตว่า AB’/ AB = AC’ / AC ทำให้ได้ว่า AC / AC’’ = AC / AC’ นั้นคือ AC’’ = AC’ ดังนั้น C’’ และ C’ เป็นจุดเดียวกัน สามเหลี่ยม ABC และ สามเหลี่ยม AB’C’ จึงคล้ายกัน
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง, 2560
กลับไปที่เนื้อหา
ทฤษฎีบทเชวาและเมเนลอส
ก่อนเข้าสู่ทฤษฎีบทของเชวาและเมเนลอส เราต้องทำความเข้าใจข้อตกลงเกี่ยวกับความยาวด้าน ถ้า AB x BC > 0 หมายความว่า AB และ BC มีทิศทางเดียวกันบนเส้นตรงเดียวกัน แต่ถ้า AB x BC < 0 แล้ว AB และ BC มีทิศตรงกันข้ามบนเส้นตรงเดียวกัน หากเราพิจารณา AB / BA = -1
พิจารณาการสร้างตามขั้นตอนต่อไปนี้
ขั้นตอนที่ 1 สร้างสามเหลี่ยม ABC
ขั้นตอนที่ 2 สร้างส่วนของเส้นตรงจากจุดยอดทั้งสามของรูปสามเหลี่ยมไปพบกับฐานที่จุด x ,y และ z ตามลำดับ และให้ส่วนของเส้นตรงทั้งสามเส้นตัดกันที่จุด P
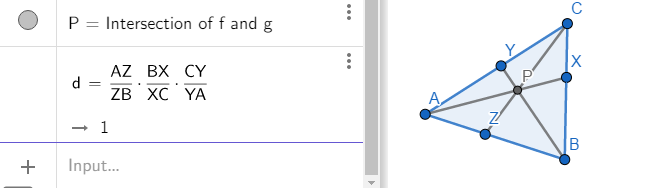
ภาพที่ 11 ภาพประกอบทฤษฎีบทเชวา
เราพบว่า ผลคูณของสัดส่วนด้าน (AZ / ZB) x (BX / XC) x (CY / YA) = 1
ในทางกลับกันกำหนดสามเหลี่ยม ABC โดยที่ AY = 3, YC = 6, CX = 2.3, XB = 4.6, BZ = 4 และ ZA = 1
ขั้นตอนที่ 1 สร้างสามเหลี่ยม ABC ที่มีความยาวด้าน
ขั้นตอนที่ 2 สร้างจุด X จุด Y และ จุด Z ตามเงื่อนไข
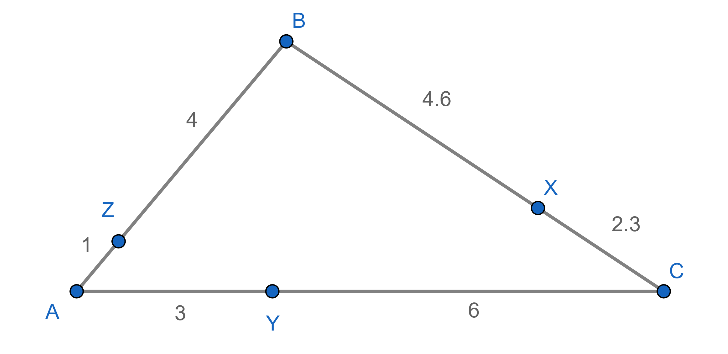
ภาพที่ 12 ภาพประกอบบทกลับของทฤษฎีบทเชวา
สังเกตว่า (AY / YC) x (CX / XB) x (BZ / ZA) = 1
ขั้นตอนที่ 3 ลากเส้น AX เส้น BY และ เส้น CZ จะพบว่าเส้นทั้งสามเส้นตัดกันที่จุดจุดเดียวดังภาพที่ 13
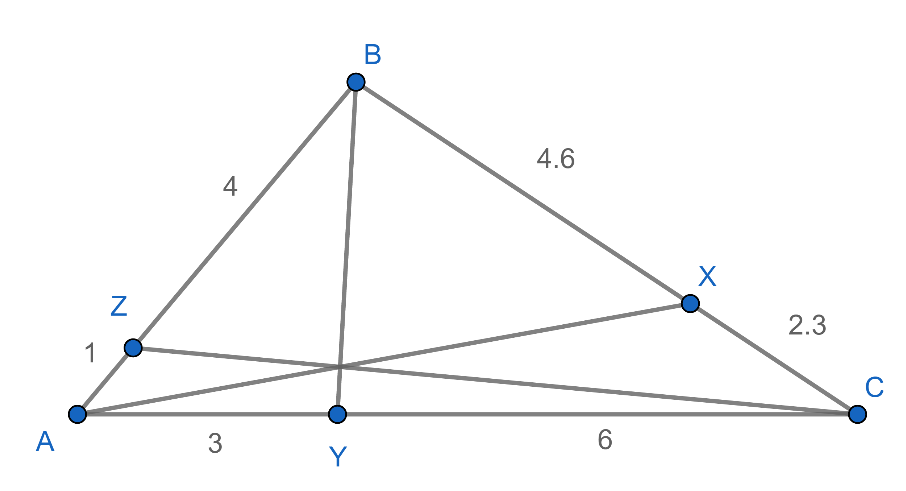
ภาพที่ 13 ข้อสรุปบทกลับทฤษฎีบทของเชวา
จากตัวอย่างข้างต้นเราเรียก เส้น AX เส้นBY และ เส้น CZ ว่าเชเวียน (cevians)
เราสรุปเป็นทฤษฎีบทได้ดังนี้
ทฤษฎีบทของเชวา กำหนดให้ สามเหลี่ยม ABC มีเส้นเชเวียนซึ่งลากจากจุดยอด จุด A จุด B และ จุด C ของรูปสาเหลี่ยมไปพบกับฐาน BC ฐาน AC และ AB ที่จุด X จุด Y และ จุด Z ตามลำดับแล้ว
เชเวียนสามเส้น { AX, BY , CZ }จะตัดกันที่จุดจุดเดียว ก็ต่อเมื่อ (AZ / ZB) x (BX/ XC) x (CY/YA) = 1
ในส่วนของการพิสูจน์ผู้เขียนขอไม่กล่าวถึง ณ ที่นี้แต่จะสรุปแนวทางการพิสูจน์โดยการพิจารณาผลคูณของสัดส่วนของพื้นที่ของรูปสามเหลี่ยมที่มีค่าเท่ากับ 1 ซึ่งผลคูณสัดส่วนของพื้นที่นั้นเท่ากันกับผลคูณของสัดส่วนด้านตามทฤษฎีบทของเชวา จึงได้ว่า ผลคูณสัดส่วนด้านมีค่าเท่ากับ 1 เช่นเดียวกัน สำหรับขากลับใช้แนวทางเดียวกันกับการพิสูจน์สามเหลี่ยมคล้ายก่อนหน้านี้คือ กำหนดให้มีรูปสามเหลี่ยมที่สอดคล้องกับขาไป จากนั้นสมมติให้มีเชเวียนที่สอดคล้องกับสมการสัดส่วนแต่มีเชเวียน 1 เส้นที่มีจุดปลายต่างออกไป แล้วแสดงให้ได้ว่าจุดปลายทั้งสองนั้นเป็นจุดเดียวกัน ผู้อ่านสามารถศึกษาเพิ่มเติมได้ในตำราเรขาคณิตขั้นสูงทั่วไป
สำหรับทฤษฎีบทของเมเนลอสนั้นจะให้สมการสัดส่วนที่คล้ายกับทฤษฎีบทของเชวาแต่จะได้ผลคูณสัดส่วนเท่ากับ -1 นั้นคือ (AZ / ZB) x (BX/ XC) x (CY/YA) = - 1 ดังนั้นทำให้ได้ข้อสรุปที่ต่างกันด้วย ในทฤษฎีบทของเมเนลอสนั้นเราจะพบว่าจุดปลาย { จุด X, จุด Y, จุด Z } ของ เส้นAX เส้นBY และ เส้นCZ นั้นอยู่ร่วมเส้นตรงเดียวกัน
พิจารณาการสร้างตามขั้นตอนต่อไปนี้
ขั้นตอนที่ 1 สร้างสามเหลี่ยม ABC
ขั้นตอนที่ 2 ลากส่วนของเส้นตรง BX และ CY จากด้าน CB และ AC
ขั้นตอนที่ 3 สร้างเส้นตรง XY
ขั้นตอนที่ 4 สร้าง BZ โดยที่จุด Z อยู่บนเส้นตรง XY
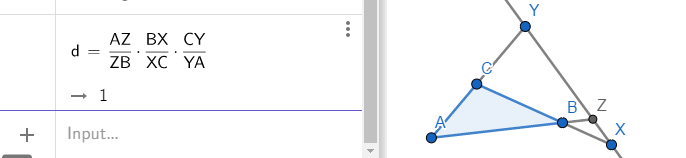
ภาพที่ 14 รูปประกอบทฤษฎีบทขาไปของเมเนลอส
จะเห็นได้ว่าสัดส่วนตามขนาดของ (AZ / ZB) x (BX / XC) x (CY / YA) = 1 แต่ตามข้อตกลงข้างต้นเรากำหนดให้ ผลคูณหรือสัดส่วนของเส้นที่ทิศตรงข้ามกันแทนด้วย -1 ดังนั้น เมื่อเราทำการพิจารณาทิศทางจะพบว่า AZ กับ ZB มีทิศทางตรงกันข้ามรวมถึง BX กับ BC และ CY กับ YA ดังนั้น
(AZ / ZB) x (BX / XC) x (CY / YA) = - 1
เป็นไปตามข้อตกลงเบื้องต้น ในทางกลับกันเราสร้างสามเหลี่ยม ABC และต่อความยาวด้านโดยกำหนดให้
AZ / ZB = 1 / 2 และ BX / XC = - 2 / 3 และให้ CY / YA = 3 / 1
ขั้นตอนที่ 1 สร้างรูปสามเหลี่ยม ABC
ขั้นตอนที่ 2 สร้างจุด Z บนด้าน AB ให้ AZ / ZB = 1 / 2
ขั้นตอนที่ 3 สร้างจุด Y บนด้าน AC ให้ CY / YA = 3 / 1
ขั้นตอนที่ 4 สร้างจุด X โดยต่อด้าน BC ให้ BX / XC = 2 / 3
จะได้รูปดังภาพที่ 15 และจะเห็นได้ว่า จุด X จุด Y และ จุด Z นั้นอยู่บนเส้นตรงเดียวกัน ดังภาพที่ 16
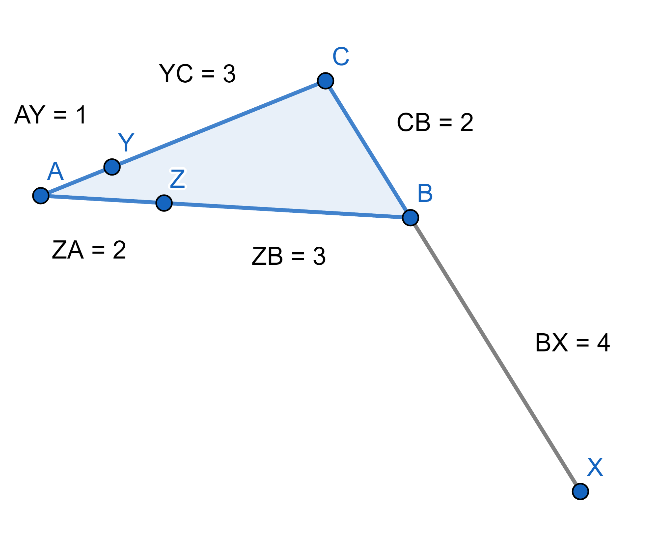
ภาพที่ 15 รูปที่ได้จากขั้นตอนการสร้างขากลับทฤษฎีบทของเมเนลอส
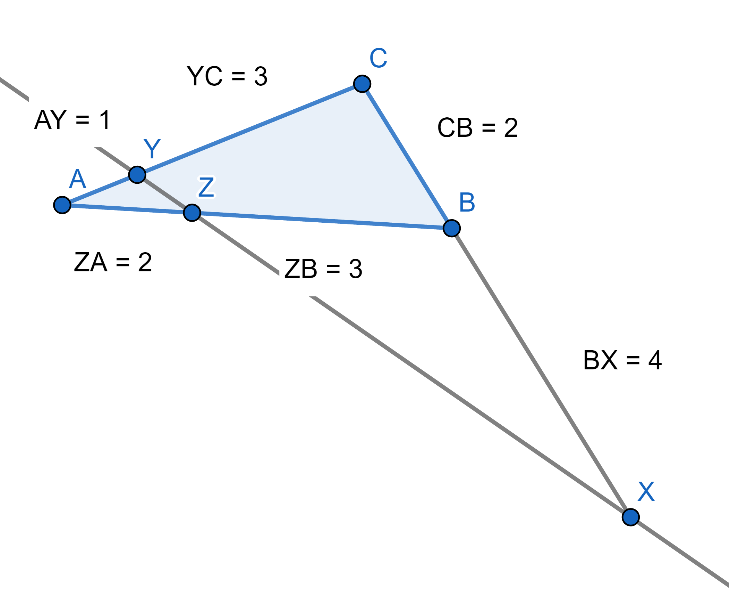
ภาพที่ 16 บทสรุปขากลับทฤษฎีของเมเนลอส
เราสรุปทฤษฎีบทของเมเนลอสได้ดังนี้
ทฤษฎีบทของเมเนลอส กำหนดให้ ABC เป็นสามเหลี่ยมใด ๆโดยที่มีจุด X จุด Y และ จุด Z อยู่บนแนวเส้นตรงเดียวกันกับฐาน BC ฐาน AC และ ฐาน AB ตามลำดับแล้ว
จุด {X, Y, Z } จะอยู่บนเส้นตรงเดียวกัน(transversal) ก็ต่อเมื่อ (AZ / ZB) x (BX / XC) x (CY / YA) = -1
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง, 2560
กลับไปที่เนื้อหา
การวัดภายในรูปสามเหลี่ยม
เมื่อเราพิจารณาถึงรูปเรขาคณิต รวมถึงรูปทรงเรขาคณิต การหาตัวแทนหรือจุดศูนย์กลางของรูปนั้นเป็นสิ่งสำคัญอย่างหนึ่งโดยเฉพาะอย่างยิ่งในวิชาฟิสิกส์ที่เราใช้จุดศูนย์กลางมวล หรือ จุดศูนย์ถ่วงเป็นตัวแทนวัตถุเป็นต้น แต่บทเรียนนี้เราจะศึกษาจุดภายในของรูปเรขาคณิตสามเหลี่ยมที่สัมพันธ์กับทฤษฎีบทของเชวาประกอบด้วย จุดเซนทรอยด์ (centroid) จุดออร์โธเซนเตอร์ (orthocenter) จุดอินเซนเตอร์ (incenter)
จุดเซนทรอยด์เป็นจุดตัดของเส้นเชเวียนสามเส้นโดยที่จุดบนด้านของรูปสามเหลี่ยมจะแบ่งครึ่งความยาวด้าน ถ้าเรากำหนดให้ ABC เป็นสามเหลี่ยมใด ๆ และมี จุด X จุด Y และ จุด Z แบ่งครึ่งด้าน AB ด้าน BC และ ด้าน AC ตามลำดับแล้วเส้นสามเส้นนี้จะตัดกันที่จุด ๆ ตามทฤษฎีบทของเชวา
(AX / XB) x (BY / YC) x (CZ / ZA) = 1/1 x 1/1 x 1/1 = 1 ดังภาพที่ 17
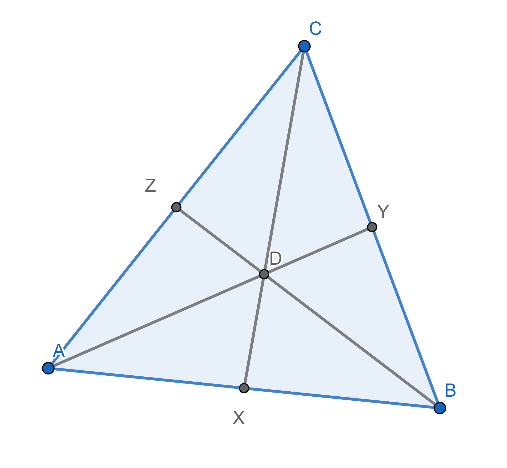
ภาพที่ 17 จุดเซนทรอยด์ของรูปสามเหลี่ยม
เราเรียกเชเวียน {AY, BZ, CX} ว่าเส้นมัธยฐาน (medians) ของสามเหลี่ยม ABC
จากภาพที่ 17 หากเราประยุกต์ใช้ทฤษฎีบทเมเนลอสพิจารณาสัดส่วน
(AB / BX) x (XD / DC) x (CZ/ZA) = -1
( -2 / 1 ) x (XD / DC) x ( 1 / 1) = -1
จะได้ว่า XD / DC = 1 / 2 นั้นคือ CD / CX = 2 / 3 ระยะทางจากจุดยอดมายังจุดเซนทรอยด์จะมีขนาด 2 ใน 3 ของเส้นมัธยฐาน
จุดออร์โธเซนเตอร์เป็นจุดตัดของเชเวียนสามเส้นเช่นเดียวกันแต่เชเวียนทั้งสามจะมีคุณสมบัติเหมือนกันคือตั้งฉากกับฐาน ถ้าเรากำหนดสามเหลี่ยม ABC เป็นสามเหลี่ยมใด ๆ และให้เส้น AX เป็นเส้นที่ตั้งฉากกับฐาน BC เส้น BY เป็นเส้นที่ตั้งฉากกับฐาน AC และ เส้น CZ ตั้งฉากกับฐาน AB แล้วเส้นตรงสามเส้นนี้จะตัดกันที่จุด ๆเดียวตามทฤษฎีบทของเชวา
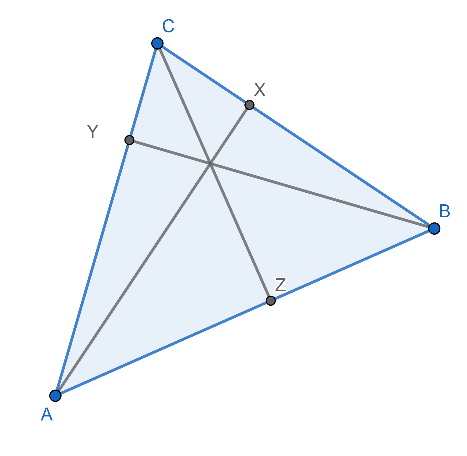
ภาพที่ 18 จุดออร์โธเซนเตอร์ของรูปสามเหลี่ยม
สังเกตว่า สามเหลี่ยม CBZ คล้ายกันกับ สามเหลี่ยม ABX จะได้
CB / AB = BZ / BX = CZ/AX = k1
สามเหลี่ยมฺ BYA คล้ายกับสามเหลี่ยม CZA จะได้
BY / CZ = YA / ZA = BA / CA = k2
สามเหลี่ยม AXC คล้ายกับสามเหลี่ยม BYC
AX / BY = XC / YC = AC / BC = k3
พิจารณา
(AZ / ZB) x (BX / XC) x (CY / YA) = (AZ / YA) x (BX / BZ) x (CY / XC)
= (AZ / YA) x (BX / BZ) x (AX / BY)
= (AZ / YA) x (BX / BZ) x (AX / CZ) x (CZ / BY)
= (1 / k2) x k1 x (1/k1) x k2
= 1
เราเรียกเชเวียน {AX, BY, CZ} ว่าอัลติจูด (altitude) ของสามเหลี่ยม ABC
จุดอินเซนเตอร์เป็นจุดที่ใช้การแบ่งครึ่งมุมยอด (Angle bisectors) แล้วได้บรรจบที่ฐาน ถ้าสามเหลี่ยม ABC มีเส้น AX แบ่งครึ่งมุม A และไปตัดกับฐาน BC ที่จุด X เส้น BY แบ่งครึ่งมุม B และไปตัดกับฐาน AC ที่จุด Y และ เส้น CZ ไปตัดกับฐาน AB ที่จุด Z จะได้ว่าเส้นตรงสามเส้นนี้ตัดกันที่จุด ๆเดียวตามทฤษฎีบทของเชวาในภาพที่ 19 ก่อนอื่นเราจะต้องพิสูจน์บทตั้งเพื่อหาความสัมพันธ์สัดส่วนด้านกับการแบ่งครึ่งมุม
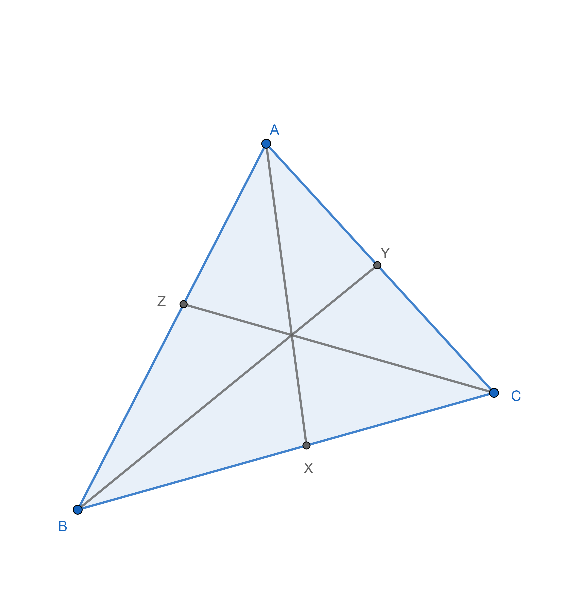
ภาพที่ 19 จุดอินเซนเตอร์ของรูปสามเหลี่ยม
บทตั้ง ให้เส้น AX เป็นเส้นแบ่งครึ่งมุม A ของสามเหลี่ยม ABC และตัดฐาน BC ที่จุด X จะได้ว่า
มุม XAC = มุม XAB ก็ต่อเมื่อ AB/AC = BX / XC
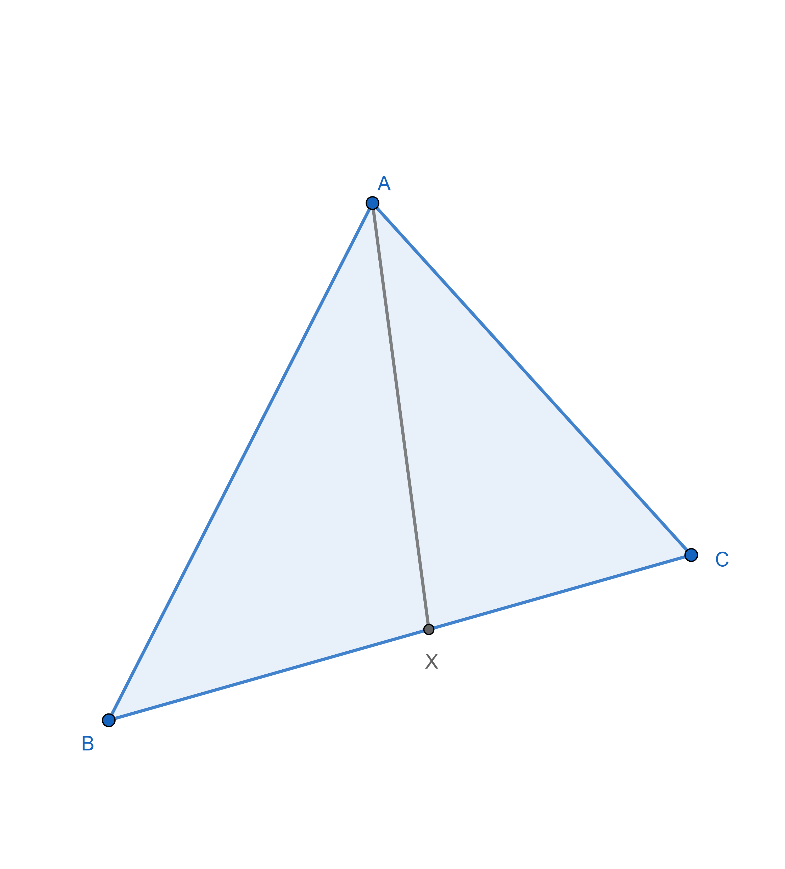
ภาพที่ 20 การแบ่งครึ่งมุม A
(ขาไป) ให้มุม XAC = มุม XAB สร้างเส้น altitude XY และ XZ โดยที่จุด Y และ Z อยู่บนด้าน BA และ AC ตามลำดับ จะได้ว่า สามเหลี่ยม AXY เท่ากับทุกประการกับสามเหลี่ยม AXZ (มุม – มุม – ด้าน) สร้าง altitude AD ตั้งฉากกับด้าน BC ที่จุด D ดังภาพที่ 21 จะได้ว่า
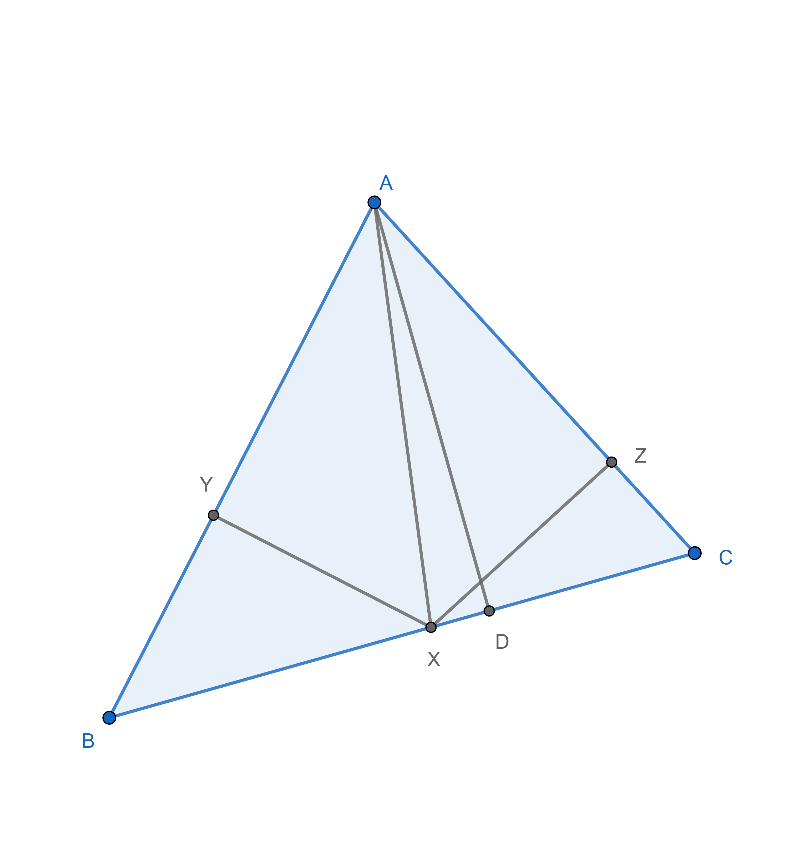
ภาพที่ 21 รูปประกอบการพิสูจน์ขาไป
สามเหลี่ยม ADB คล้ายกับสามเหลี่ยม XYB นั้นคือ AD / XY = DB / YB = AB / XB
สามเหลี่ยม ADC คล้ายกับสามเหลี่ยม XZC นั้นคือ AD / XZ = DC / ZC = AC / XC
เนื่องจาก XY = XZ จะได้ว่า AB / XB = AD / XY = AD / XZ = AC / XC
ดังนั้น AB / AC = XB / XC
(ขากลับ) สมมติให้ AB / AC = XB / XC กำหนดให้ สามเหลี่ยม ABC มีเส้น AX’ แบ่งครึ่งมุมดังภาพที่ 22
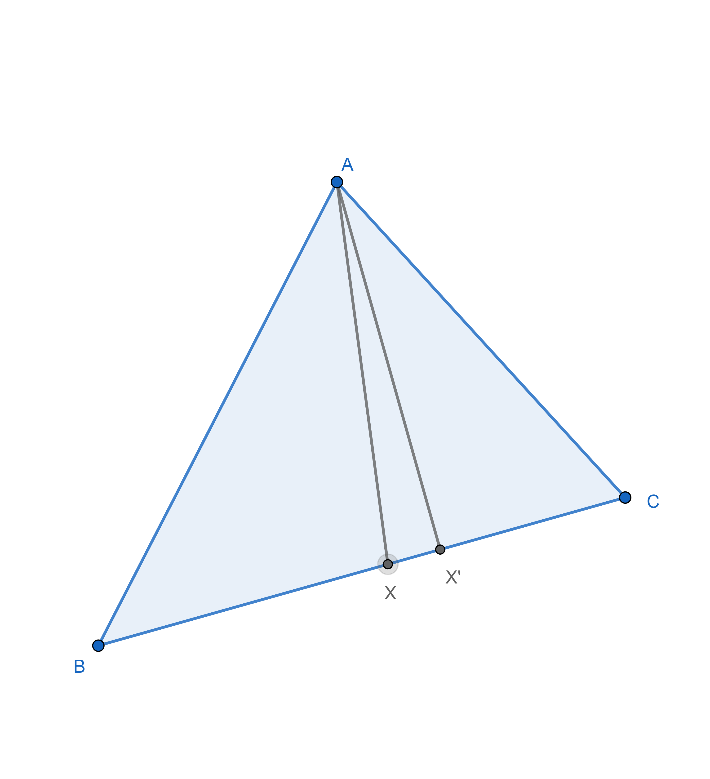
ภาพที่ 22 ภาพประกอบการพิสูจน์ขากลับ
จะได้ว่า AB / AC = X’B / X’C จะเห็นว่า X’B / X’C = XB / XC นั้นคือ X’ และ X เป็นจุดเดียวกันทำให้ มุม AXB = มุมAXC
เรานำผลที่ได้นี้ไปพิสูจน์ต่อว่าเส้นแบ่งครึ่งมุมของสามเหลี่ยมเป็นเส้นเชเวียน
พิจารณา (BX / XC) x (CY / YA) x (AZ / ZB) = (AB / AC) x (BC / BA) x (AC / CB) = 1
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง, 2560
กลับไปที่เนื้อหา
กฎของไซน์และโคไซน์
สามเหลี่ยมมุมฉาก ABC ที่มีมุม A เป็นมุมฉากดังภาพที่ 23
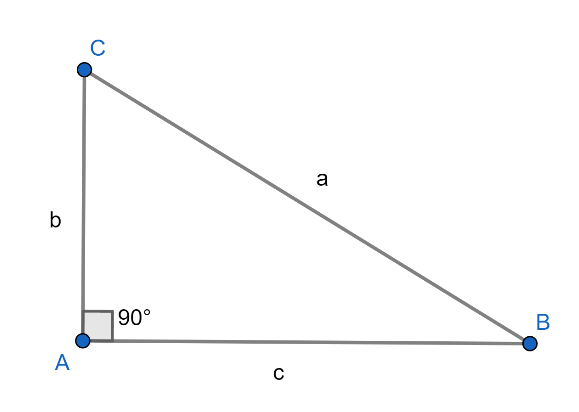
ภาพที่ 23 รูปสามเหลี่ยมมุมฉาก ABC มีมุม A เป็นมุมฉาก
จากทฤษฎีบทพิธาโกรัสเป็นการศึกษารูปสามเหลี่ยมมุมฉากแต่เป็นการศึกษารูปแบบความสัมพันธ์ของความยาวด้านทั้งสามในรูปสมการ a2 = b2 + c2 แต่ในตรีโกณมิตินั้นจะเป็นการศึกษาความสัมพันธ์ของสัดส่วนด้าน และมุม ในที่นี้เราจะเรียกมุม ABC ด้วย มุมB พิจารณาความยาวด้านเราจะพบว่ามีจำนวนสามจำนวนคือ a , b และ c นำมาพิจารณาสัดส่วนได้ 6 แบบคือ
1) a/b 2) a/c 3) b/c 4) b/a 5) c/a 6) c/b
พิจารณาความสัมพันธ์ของด้านกับมุม B จะพบว่า ด้านที่มีความยาว b เป็นด้านตรงข้ามมุม B ด้านที่มีความยาว a และ c เป็นด้านประชิดมุมฺ B แต่ด้านที่มีความยาว a เป็นด้านตรงข้ามมุมฉาก เรานิยามสัดส่วน
b/a เป็นสัดส่วนด้านตรงข้ามมุม B กับ ด้านตรงข้ามมุมฉากเรียกว่า ไซน์ (sine) แทนด้วย sin B
c/a เป็นสัดส่วนด้านประกอบมุม B กับ ด้านตรงข้ามมุมฉากเรียกว่า โคไซน์ (cosine) แทนด้วย cos B
b/c เป็นสัดส่วนด้านตรงข้ามมุม B กับ ด้านประชิดมุม B เรียกว่า แทนแจนท์ (tangent) แทนด้วย tan B
พิจารณาส่วนกลับของสัดส่วนทั้ง 3 เราจะเรียกค่า a/b ว่าโคเซแคนท์ (cosecant) เรียก a/c ว่าเซแคนท์ (secant) และ เรียก c/b ว่าโคแทนเจนท์ (cotangent) อย่างไรก็ตามฟังก์ชัน tan sec cosec cot นี้สามารถเขียนได้ในรูปของ sin และ cos ดังนี้
tan B = (sin B) / (cos B) sec B = 1 / (cos B)
cosec B = 1 / (sin B) cot B = (cos B) / (sin B)
นอกจากนี้เมื่อพิจารณาสมการ a2 = b2 + c2 เมื่อนำ a2 หารตลอดเราจะพบว่า (b/a)2 + (c/a)2 = 1 นั้นคือ
(sin B)2 + (cos B)2 = 1
หากพิจารณาวงกลมในระบบพิกัดฉากดังภาพที่ 24
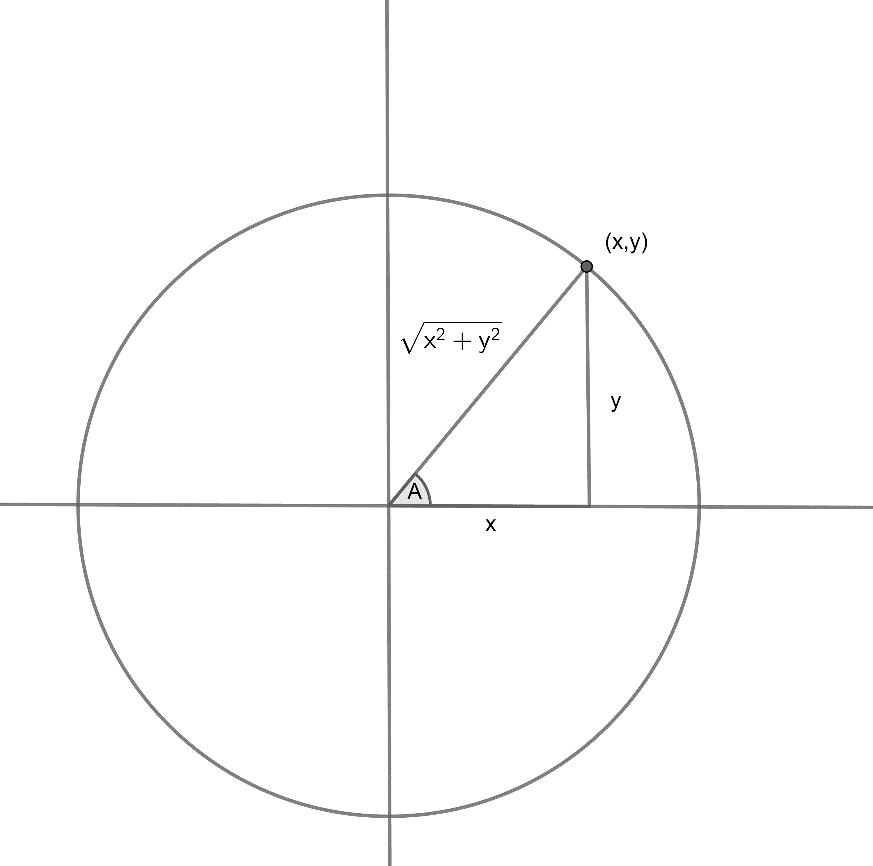
ภาพที่ 24 ตรีโกณมิติในวงกลมรัศมี (x2 + y2)1/2
จะได้ว่า
sin A = y / (x2 + y2)1/2 และ cos A = x / (x2 + y2)1/2
กรณีที่ มุมA มีค่าอยู่ในช่วง (90 องศา, 180 องศา) ดังภาพที่ 25
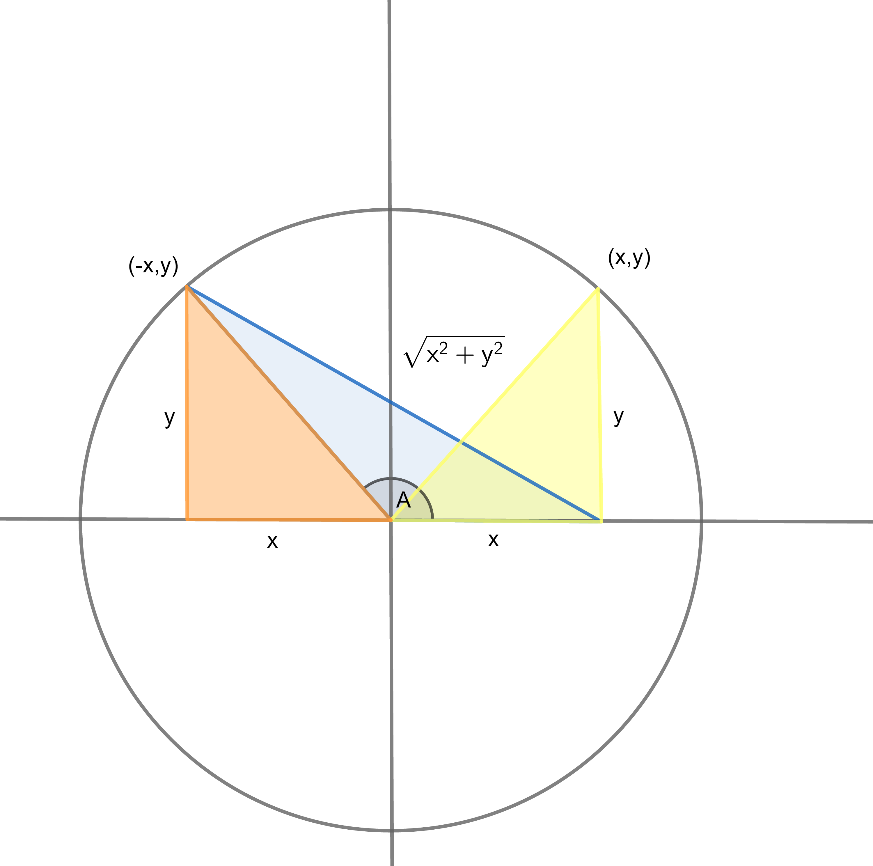
ภาพที่ 25 ตรีโกณมิติในวงกลมรัศมี (x2 + y2)1/2 เมื่อมุมA มีค่าอยู่ในช่วง (90 องศา, 180 องศา)
พิจารณาสามเหลี่ยมสีแดงจะเห็นว่า
sin (180 – A) = y / (x2 + y2)1/2 = sin A แต่ cos (180 – A) = (- x) / (x2 + y2)1/2 = - cos A
สำหรับ A ที่อยู่ในช่วง (180 องศา, 270 องศา) และ (270 องศา, 360 องศา) พิจารณาในทำนองเดียวกันจะได้
sin (180 + A) = - sin (A) และ cos (180 + A) = - cos (A)
sin (360 - A) = - sin (A) แต่ cos (360 - A) = cos (A)
แม้ว่าอัตราส่วนตรีโกณมิติเริ่มต้นจากการศึกษาสามเหลี่ยมมุมฉากแต่เราสามารถขยายผลไปสู่สามเหลี่ยมใด ๆผ่านการศึกษากฎของไซน์ (Law of sine) ซึ่งกล่าวถึงสัดส่วนของค่าฟังก์ชันไซน์และด้านรองรับมุม และกฏของโคไซน์ (Law of cosine) ซึ่งแสดงถีงความสัมพันธ์ของด้านทั้งสามกับค่าฟังก์ชันโคไซน์
กฏของไซน์
กำหนดสามเหลี่ยม ABC เป็นสามเหลี่ยม ภาพที่ 26 แสดงให้เห็นว่าสัดส่วน sin A / a, sin B / b และ sin C / c มีค่าเท่ากันคือ 0.1
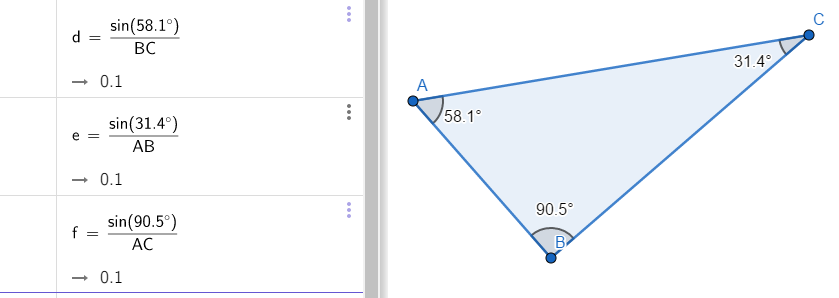
ภาพที่ 26 การประยุกต์ใช้กฎไซน์กับสามเหลี่ยม ABC
ต่อไปเราจะทำการวางนัยยะทั่วไปโดยพิจารณาสามเหลี่ยม ABC ใด ๆ สร้างเส้น altitude 3 เส้นดังภาพที่ 27
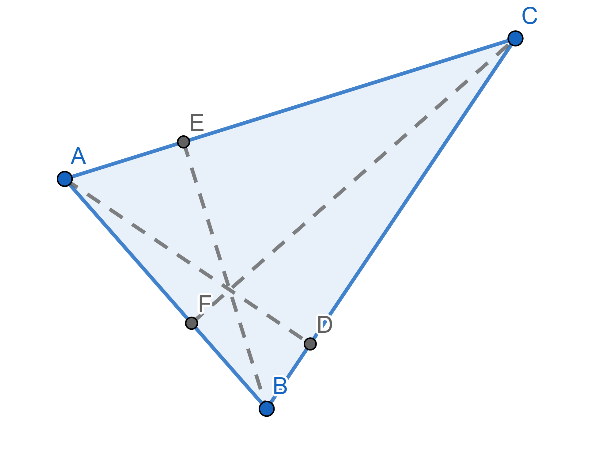
ภาพที่ 27 เส้น altitude ทั้งสามของรูปสามเหลี่ยม ABC
พิจารณาการพื้นที่ของรูปสามเหลี่ยม ABC
กรณีที่ใช้ AB เป็นฐาน จะได้
พื้นที่ = (CF x AB) / 2 = (sin B x BC x AB) / 2 = (sin A x AC x AB) / 2
จะเห็นว่า sin B x BC = sin A x AC นั้นคือ sin B / AC = sin A / BC
กรณีที่ใช้ AC เป็นฐาน จะได้
พื้นที่ = (EB x AC) / 2 = (sin A x AB x AC) / 2 = (sin C x BC x AC) / 2
จะเห็นว่า sin A x AB = sin C x BC นั้นคือ sin A / BC = sin C / AB
ดังนั้น sin B / AC = sin A / BC = sin C / AB
ถ้าให้ ด้าน AC ยาว b หน่วย ด้าน BC ยาว a หน่วย และด้าน AB ยาว c หน่วยจะได้ sin B / b = sin A / a = sin C / c
กฎของโคไซน์
จากภาพที่ 28 เราจะเห็นว่า
AB2 = c2 = 16.5 BC2 = a2 = 35 AC2 = b2 = 72.5 และ cos B = - 0.4
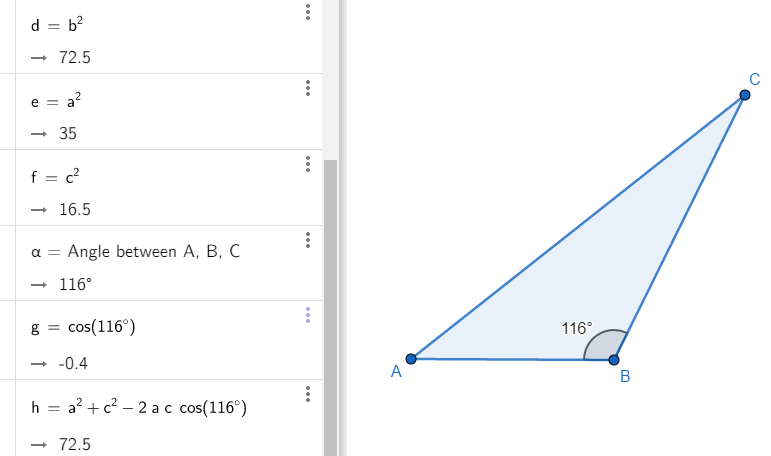
ภาพที่ 28 ภาพแสดงกฏของโคไซน์
สังเกต d และ h เป็นไปตามสมการกฎของโคไซน์
AC2 = AB2 + BC2 – 2 x AB x BC x cos B
ในทำนองเดียวกันสำหรับการพิจารณา cos A และ cos C จะได้
a2 = b2 + c2 – 2bc(cos A)
b2 = a2 + c2 – 2ac(cos B)
c2 = a2 + b2 – 2ab(cos C)
สามารถพิสูจน์กรณีวางนัยยะทั่วไปได้ดังนี้
พิจารณาสามเหลี่ยม ABC จากนั้นลากจุดยอด C ลงมาตั้งฉากกับฐานที่จุด D ดังภาพที่ 29
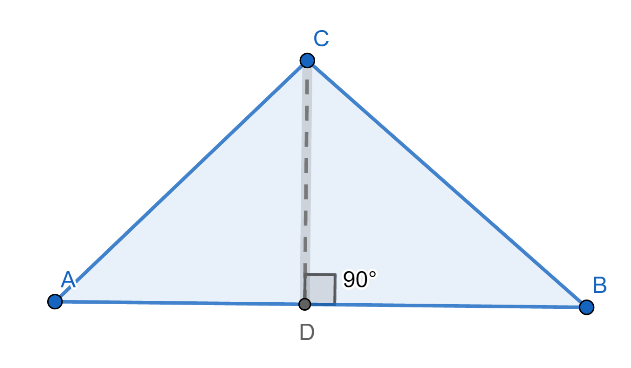
ภาพที่ 29 ภาพประกอบการพิสูจน์กฏของโคไซน์
เมื่อให้หลักการตรีโกณมิติจะได้ว่า สามเหลี่ยมนี้มีความสูง CD = a sin B และ มีความยาวด้าน DB = a cos B
จากนั้นประยุกต์ใช้หลักการพิธาโกรัสกับสามเหลี่ยม ACD จะได้
b2 = (c – a x cos B)2 + a2(sin B)2
= c2 – 2ac(cos B) + a2(cos B)2 + a2(sin B)2
= c2 – 2ac(cos B) + a2[(cos B)2 + (sin B)2]
= a2 + c2 – 2ac(cos B)
สำหรับมุม A และ B สามารถพิสูจน์ได้ในทำนองเดียวกัน ถ้ารูปสามเหลี่ยมเป็นดังภาพที่ 30
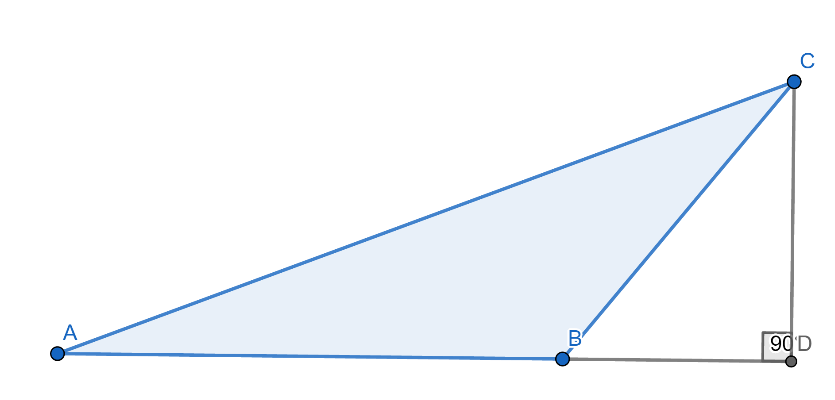
ภาพที่ 30 ภาพประกอบการพิสูจน์กฎของโคไซน์
เนื่องจากมุม B มีค่าอยู่ในช่วง (90 องศา , 180 องศา) จะได้ว่า
sin (180 – B) = sin B แต่ cos (180 – B ) = - cos B
จากภาพที่ 30 จะได้สมการ
b2 = (c + a x cos (180 – B))2 + a2(sin (180 – B))2
= (c - a x cos B)2 + a2(sin B)2
= c2 – 2ac(cos B) + a2(cos B)2 + a2(sin B)2
= c2 – 2ac(cos B) + a2[(cos B)2 + (sin B)2]
= a2 + c2 – 2ac(cos B)
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง, 2560
กลับไปที่เนื้อหา
ทฤษฎีบทของสจ๊วตและอพอลโลเนียส
จากบทเรียนก่อนหน้านี้ เราจะเห็นว่ารูปเรขาคณิตรูปสามเหลี่ยมสามารถอธิบาย วัด หรือ คำนวณผ่านตัวแทนพีชคณิตซึ่งออกมาในรูปของตัวแปรและการดำเนินการในบทนี้เราจะศึกษาทฤษฎีของสจ๊วต และ อพอลโลเนียส เป็นการศึกษารูปเรขาคณิตสามเหลี่ยมในเชิงพีชคณิตรูปแบบหนึ่ง โดยมีปริมาณเกี่ยวข้องประกอบด้วยความยาวด้าน และเส้นที่ลากจากจุดยอดไปยังฐาน 1 เส้น
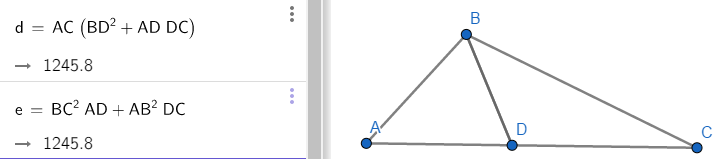
ภาพที่ 31 ภาพตัวอย่างทฤษฎีของสจ๊วต
จากภาพที่ 31 เราพบว่าความสัมพันธ์ของเส้นทั้ง 6 เส้นคือ เส้น AB เส้น BC เส้น AC เส้น BD เส้น AD และ เส้น DC สอดคล้องกับสมการ
AC x (BD2 + AD x DC) = (BC2 x AD) + (AB2 x DC)
เพื่อทำการพิสูจน์แบบวางนัยยะทั่วไปเรากำหนดให้เส้น AB มีขนาด c หน่วย เส้น BC มีขนาด a หน่วย เส้น AC มีขนาด b หน่วย เส้น BD มีขนาด p หน่วย เส้น AD มีขนาด x หน่วย และ เส้น DC มีขนาด y หน่วยดังภาพที่ 32 จะแสดงว่า b(p2 + xy) = a2x + c2y
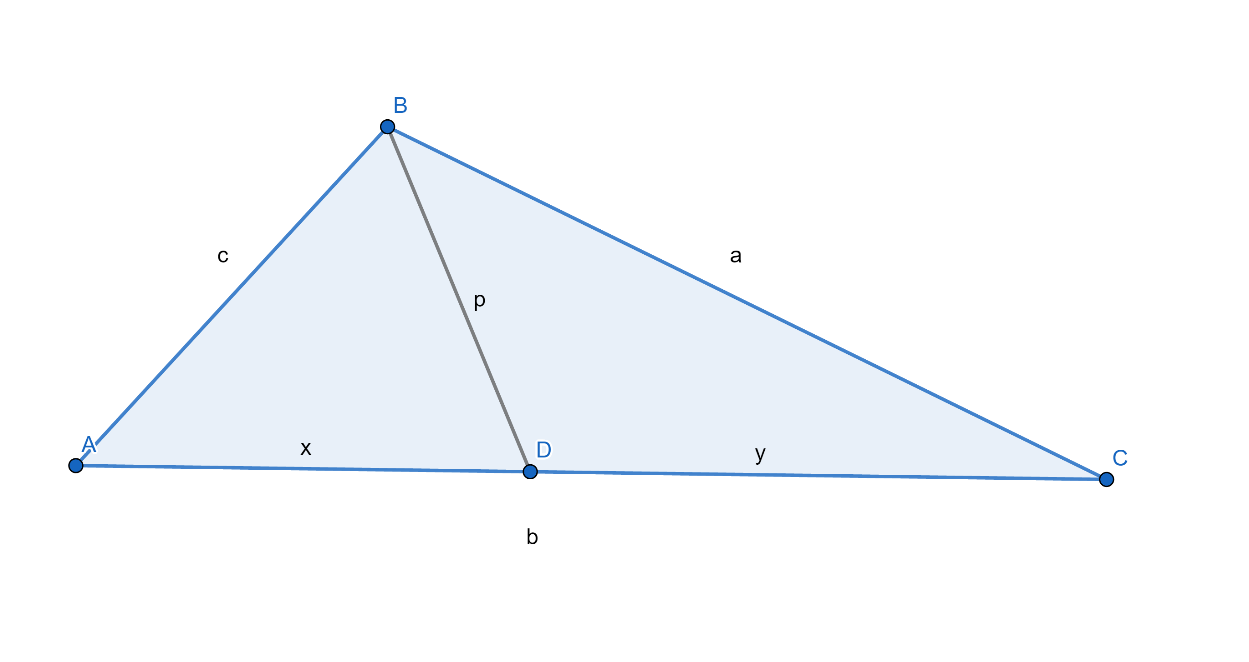
ภาพที่ 32 ภาพประกอบการพิสูจน์
พิจารณามุม D ของสามเหลี่ยม ADB จากกฎของโคไซน์ D จะได้
c2 = x2 + p2 – 2xp(cos D)
ในทำนองเดียวกับประยุกต์ใช้กฎของโคไซน์มุม D กับสามเหลี่ยม BDC จะได้
a2 = p2 + y2 - 2py(cos 180 - D) = p2 + y2 + 2py(cos D)
จะเห็นได้ว่า cos D = (x2 + p2 - c2) / (2xp) ในขณะเดียวกัน cos D = (a2 - p2 - y2) / (2py) ดังนั้น
(x2 + p2 - c2) / (2xp) = (a2 - p2 - y2) / (2py)
y(x2 + p2 - c2) = x(a2 - p2 - y2)
yx2 + yp2 - yc2 = xa2 - xp2 - xy2
yx2+ xy2 + yp2 + xp2 = xa2 + yc2
(x + y)xy + p2(x + y) = xa2 + yc2
(x + y)(p2 + xy) = xa2 + yc2
เนื่องจาก b = x+y จะได้สมการ b(p2 + xy) = xa2 + yc2
สำหรับแนวคิดทฤษฎีบทของอพอลโลเนียสนั้น เขาได้กำหนดให้เส้น BD เป็นเส้นมัธยฐานส่งผลให้ AD = DC นั้นคือ x = y = b / 2จากสูตรของสจีวตเมื่อ x = y = b / 2 จะได้
b(p2 + b2 / 4) = (b / 2)a2 + (b / 2)c2 = (b/2)(a2 + c2)
นั้นคือ p2 + b2 / 4 = (1/2)(a2 + c2)
2p2 + b2 / 2 = a2 + c2
นอกจากนี้หากเราพิจารณาในกรณีที่สามเหลี่ยมนี้เป็นสามเหลี่ยมหน้าจั่วจะได้ว่า a = c
b(p2 + xy) = xa2 + yc2 = a2(x+y) = a2b
จะได้ p2 + xy = a2
หากเพิ่มเงื่อนไขสามเหลี่ยม ABC เป็นสามเหลี่ยมหน้าจั่ว และ BD เป็นเส้นมัธยฐานจะได้
p2 + (b/2)2= a2
สามเหลี่ยมทอง (the golden triangle)
กำหนดให้ ABC เป็นสามเหลี่ยมใด ๆดังภาพที่ 33 จะเห็นว่าสามเหลี่ยม ABD เป็นสามเหลี่ยมหน้าจั่ว นอกจากนี้ยังพบว่ามุม A มีขนาด 2\theta ทำให้ได้ว่าสามเหลี่ยม ABC เป็นสามหลี่ยมหน้าจั่วเช่นเดียวกัน สัดส่วนของทองคือค่า y / x
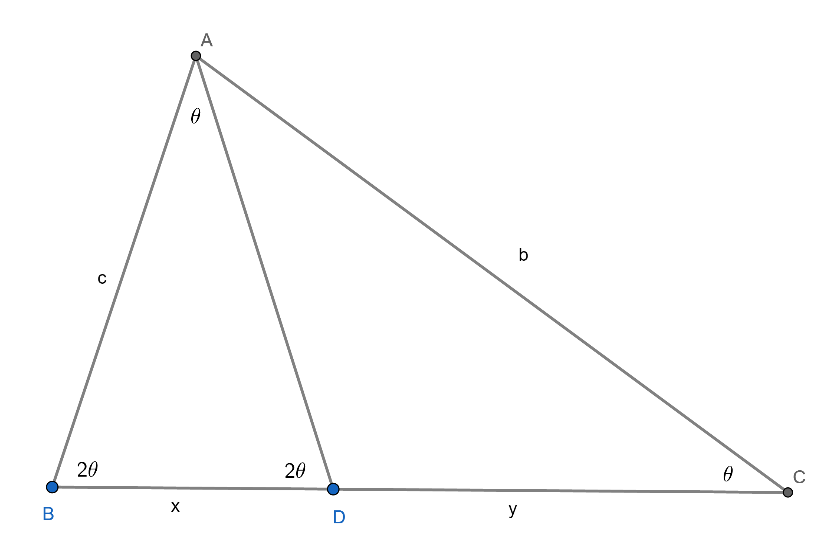
ภาพที่ 33 ภาพสำหรับพิสูจน์สามเหลี่ยมทองคำ
เนื่องจากสามเหลี่ยม ABD เป็นสามเหลี่ยมหน้าจั่วจะได้ AD = c และ ADC เป็นสามเหลี่ยมหน้าจั่วเช่นเดียวกันทำให้ DC = y = c รวมถึงสามเหลี่ยม ABC เป็นสามเหลี่ยมหน้าจั่วเช่นเดียวกันทำให้ได้ว่า x + y = x + c = b
เราสามารถประยุกต์ใช้ทฤษฎีบทสจ๊วตกับรูปที่ 13 เพื่อหาสัดส่วนทองได้ พิจารณาสมการตามทฤษฎีบทของสจ๊วตสำหรับภาพที่ 33 คือ
(x + y) x (c2 + xy) = c2y + b2x
แทนค่าคุณสมบัติที่ได้จากการเป็นสามเหลี่ยมหน้าจั่วจะได้สมการใหม่คือ
b x (c2 + xc) = c3 + b2x
b x c(c + x) = c3 + b2x
b2c = c3 + b2x
ต้องการหาสัดส่วน r = c / x พิจารณา b = x + c ดังนั้น b/x = 1 + c / x = 1 + r เราจึงหารด้วย x3 ตลอดสมการจะได้
(b / x)2(c / x) = (c / x)3 + ( b/ x)2
r (1 + r)2 = r3 + (1 + r)2
(1 + r)2(r – 1) – r3 = 0
ลดรูปนิพจน์ข้างต้นและเขียนให้อยู่ในรูปอย่างง่ายจะได้สมการพหุนาม r2 – r – 1 = 0 และทราบว่า
r = [1 + \sqrt(5)] / 2 หรือ r = [1 – \sqrt(5)] / 2
แต่ c และ x เป็นความยาวส่วนของเส้นตรงของรูปสามเหลี่ยมนั้นคือ c > 0 และ x > 0 ดังนั้น r = c / x > 0 สรุปได้ว่า r มีเพียงคำตอบเดียวคือ [1 + \sqrt(5)] / 2 เราเรียกสัดส่วนนี้กว่าสัดส่วนทอง จากรูปที่กำหนดมาให้ในภาพที่ 33 เราสามารถหาค่ามุม theta ได้จากข้อเท็จจริงที่ของมุมภายในของรูปสามเหลี่ยมเท่ากับ 180 องศาจึงได้ว่า 5 theta = 180 องศา ดังนั้น theta = 36 องศา หากเราให้กฎของไซน์กับรูปสามเหลี่ยม ABD จะพบว่า sin 72 / c = sin 36 / x
จึงได้สัดส่วนของ r = c / x = sin 72 / sin 36 = [1 + \sqrt(5)] / 2
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง, 2560
กลับไปที่เนื้อหา
เรขาคณิตของวงกลม
รูปสามเหลี่ยมแนบในวงกลม ตามที่ได้กล่าวไว้แล้วในหัวข้อที่ 1 ว่ามุมในครึ่งวงกลมคือมุมฉาก เราสามารถพิสูจน์ข้อความนี้ได้โดยพิจารณารูปสามเหลี่ยมที่แนบในวงกลมโดยที่มีเส้นผ่านศูนย์กลางของวงกลมเป็นด้านด้านหนึ่งดังภาพที่ 34
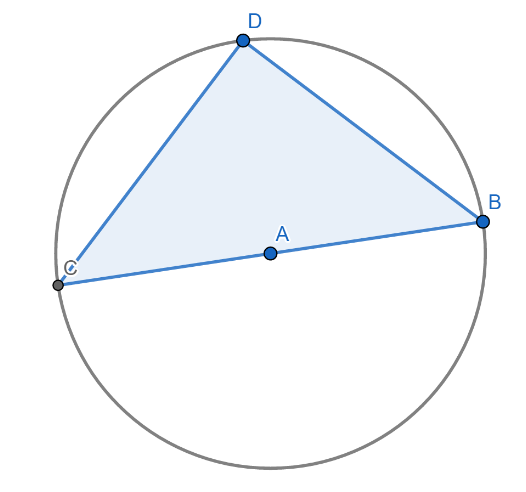
ภาพที่ 34 รูปสามเหลี่ยมแนบในวงกลมที่มีเส้นด้านศูนย์กลางเป็นด้านหนึ่งของรูปสามเหลี่ยม
เราจะพิสูจน์ว่าสามเหลี่ยมนี้เป็นสามเหลี่ยมมุมฉากสร้างส่วนของเส้นตรง DA จะเห็นว่าสามเหลี่ยม ACD เป็นและสามเหลี่ยม ABD เป็นสามเหลี่ยมหน้าจั่วเนื่องจากมีรัศมีของวงกลมเป็นด้านคู่ที่เท่ากันส่งผลให้
มุม ACD = ADC และ มุม ADB = ABD
พิจารณาผลรวมของมุมภายในของรูปสามเหลี่ยม BCD จะพบว่า
มุม BCD + มุม CDB + มุม DBC = 180
แทนค่ามุม CDB สามเหลี่ยมรูปใหญ่ด้วยมุมของสามเหลี่ยมรูปเล็กจะได้
มุม ACD + มุม CDA + มุม ADB+ มุม ABD = 180
จากนั้นแทนค่าด้วยมุมที่เท่ากัน
2(มุม CDA) + 2(มุม ADB) = 180
มุม CDA + มุม ADB = 90
สรุปได้ว่า สามเหลี่ยม BCD เป็นสามเหลี่ยมมุมฉาก
วงกลมของอพอลโลเนียส
สมมติให้ c เป็นค่าคงที่ที่ไม่เท่ากับ 1 ให้ A และ B เป็นจุดใด ๆแล้วเซต { P, PA/PB = c} เป็นรูปวงกลม
ขั้นตอนที่ 1 สร้างส่วนของเส้นตรง AB
ขั้นตอนที่ 2 สร้างจุด P โดยกำหนดให้ความยาวของ PA ไม่เท่ากับ ความยาวของ PB
ขั้นตอนที่ 3 แบ่งครึ่งมุม P ของสามเหลี่ยม APB จะได้จุด P1 บนฐาน AB
ขั้นตอนที่ 4 แบ่งครึ่งมุมที่ประชิดมุม P ในขั้นตอนที่ 3 แล้วไปตัดเส้น AB ที่จุด P2 ดังภาพที่ 35
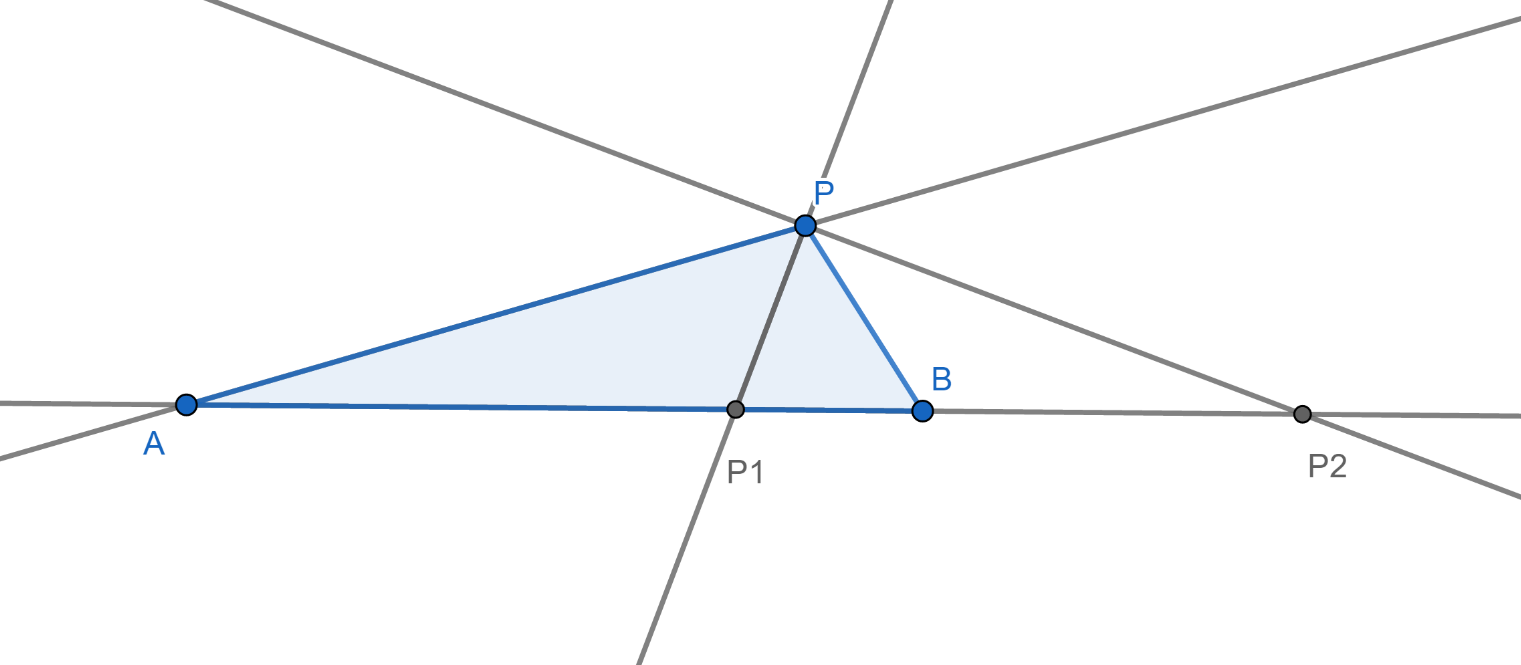
ภาพที่ 35 ภาพประกอบการสร้างขึ้นตอนที่ 1 – 4
ต่อไปเราจะแสดงว่า สามเหลี่ยม P1PP2 เป็นสามเหลี่ยมมุมฉาก ทฤษฎีแบ่งครึ่งมุมพบว่า AP1 / P1B = AP / PB = c
สังเกตว่า มุม APP1 + มุม P1PB + 2มุม BPP2 = 180 องศา แต่ มุม APP1 = มุม P1PB จึงได้ว่า มุม P1PB + มุม BPP2 = 90 องศา
ดังนั้น P1PP2 เป็นสามเหลี่ยมมุมฉาก จากทฤษฎีบทก่อนหน้านี้เราทราบว่าสามเหลี่ยมที่แนบในวงกลมที่มีเส้นผ่านศูนย์กลางเป็นด้านด้านหนึ่งจะเป็นรูปสามเหลี่ยมมุมฉาก ด้วยแนวคิดนี้เราสร้างสามารถสร้างเซตของจุด P ที่ทำให้ P1PP2 เป็นสามเหลี่ยมมุมฉาก และการรวบรวมสะสมของสามเหลี่ยมมุมฉากนี้จะได้วงกลมที่มีเส้นผ่านศูนย์กลางคือส่วนของเส้นตรง P1P2 ดังภาพที่ 36 ดังนั้นเซต { P, PA/PB = c} = เซต { P, P1PP2 เป็นสามเหลี่ยมมุมฉาก } = เซตของจุดบนวงกลม
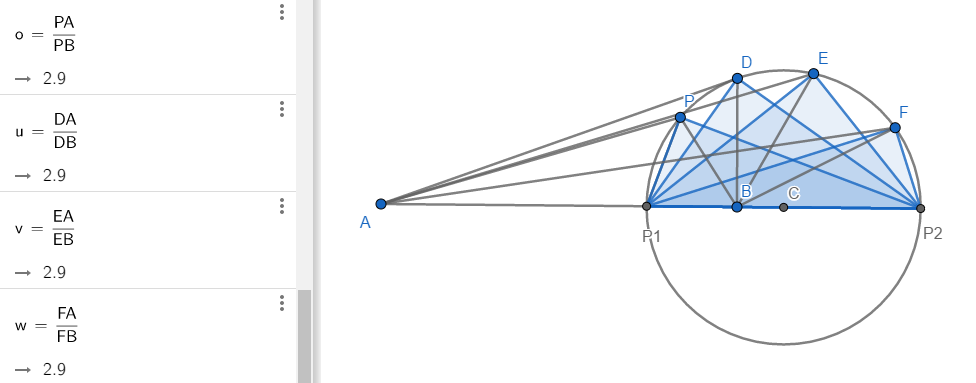
ภาพที่ 36 การสร้างวงกลมตามแนวคิดของอพอลโลเนียส
ทฤษฎีบทของสไตเนอร์
ก่อนจะทำการศึกษาทฤษฎีบทของสไตเนอร์ผู้เขียนจะทบทวนทฤษฎีบทสำคัญของมุมที่แนบในรูปวงกลมในภาพที่ 37
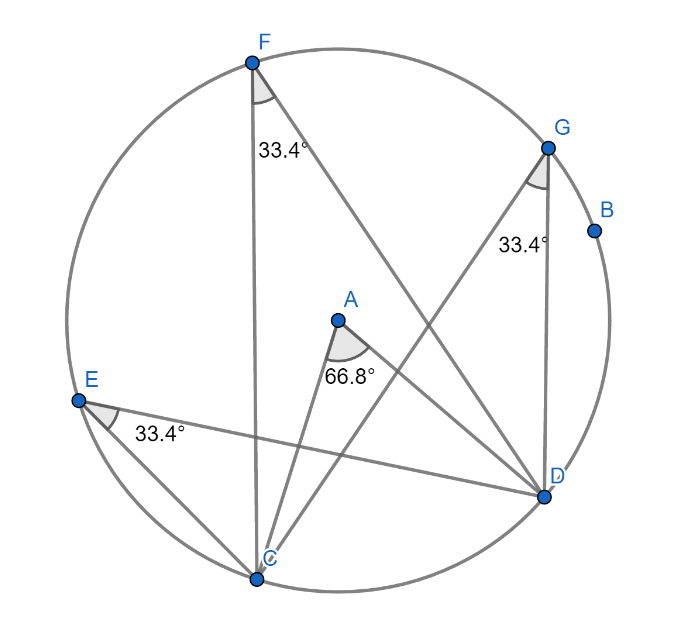
ภาพที่ 37 ภาพประกอบทฤษฎีมุมที่แนบในรูปวงกลม
จะเห็นมุมที่จุดศูนย์กลางมีค่าเป็นสองเท่าของมุมที่แนบในวงกลมที่รองรับส่วนโค้งเดียวกัน นอกจากนี้พบว่ามุมที่แนบในวงกลมที่รองรับส่วนโค้งเดียวกันจะมีค่าเท่ากับ
สำหรับทฤษฎีของสไตเนอร์เป็นการศึกษาเส้นตัดและเส้นสัมผัสวงกลม กำหนดให้ P เป็นจุดนอกวงกลมและมีส่วนของเส้นตรง PC สัมผัสวงกลม ส่วนของเส้นตรง PA และ PB ตัดกับวงกลมแล้ว
PC2 = PA x PB

ภาพที่ 38 ภาพประกอบทฤษฎีบทเส้นสัมผัสและเส้นตัด
แหล่งที่มา
Hillman A.P. and Alexanderson G.L. (1971). Algebra to Problem Solving. Allyn and Bacon, Inc. USA.
Smith K.J., (1992). Collage Mathematics and Calculus with Applications to Management, Life and Social sciences 2nd edition. Brooks/Cole Publishing company. USA.
ญาณพล แสงสันต์ และคณะ เอกสารประกอบการบรรยาย การจัดการการลงทุน มหาวิทยาลัยรามคำแหง, 2560
กลับไปที่เนื้อหา



