ลำดับ และอนุกรม (Sequences & Series)
1. ลำดับและการเขียนลำดับ
ลำดับ (Sequences) หมายถึง ตัวเลขชุดหนึ่งที่เขียนเรียงกันภายใต้กฎเกณฑ์ที่กำหนดให้
นิยาม : ฟังก์ชันที่มีโดเมน (Domain) (สมาชิกตัวหน้า) เป็นเซตของจำนวนเต็มบวกที่เรียงจากน้อยไปมากโดยเริ่มตั้งแต่ 1 และมีเรนจ์ (Range) (สมาชิกตัวหลัง) เป็นเซตของจำนวนจริง
แบ่งออกเป็น 2 ชนิด คือ
1. ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก { 1, 2, 3, …, n } เรียกว่า ลำดับจำกัด (Finite Sequence)
2. ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก { 1, 2, 3, … } เรียกว่า ลำดับอนันต์ (Infinite Sequence)
โดยทั่วไปแล้วการเขียนฟังก์ชันเรามักจะใช้ตัว f, g ,h เป็นตัวบอกฟังก์ชัน แต่สำหรับลำดับ จะใช้ตัว a ในการเขียนแทน นั่นคือ a(x) หรือสามารถเขียนแทนได้ด้วย ax เช่น a(1) แทนด้วย a1 , a(n) แทนด้วย an เป็นต้น
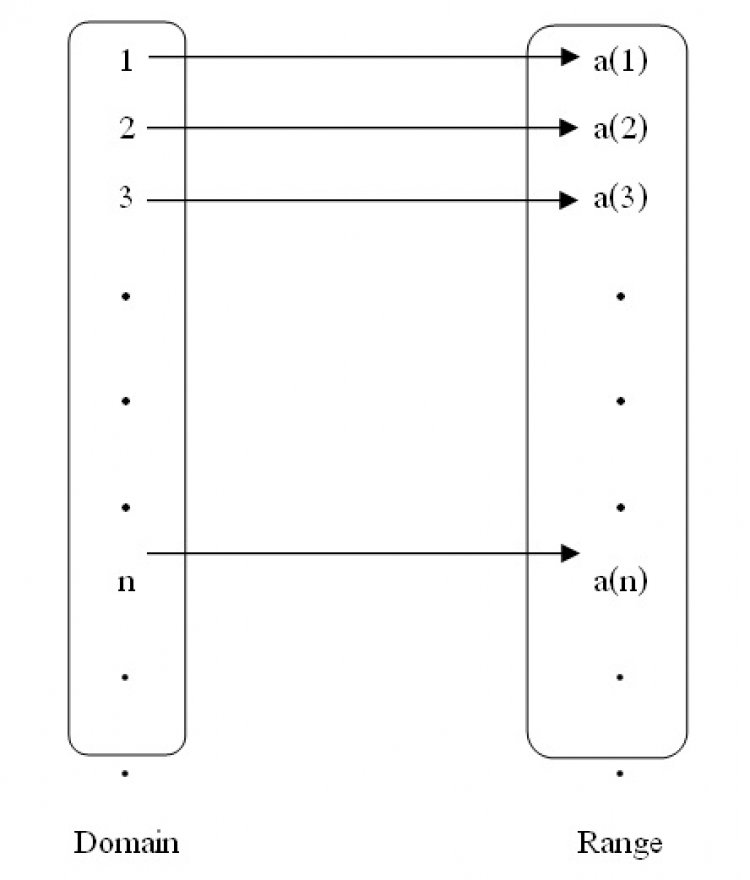
การเรียกชื่อลำดับ
เรียกแต่ละตัวว่า “พจน์” เรียงลำดับกันไป
{(1, 1), (2, 2), (3, 3), …, (n, a(n))}
เรียก (1, 1) ว่า พจน์ที่ 1 ของลำดับ
เรียก (2, 2) ว่า พจน์ที่ 2 ของลำดับ
.
.
.
เรียก (n, a(n)) ว่า พจน์ที่ n ของลำดับ หรือพจน์ทั่วไป
การเขียนลำดับ
การเขียนลำดับจะคล้ายการเขียนฟังก์ชัน แต่จะมีลักษณะการเขียนที่เพิ่มจากการเขียนฟังก์ชันปกติ ได้แก่
1. การเขียนลำดับแบบแจกแจงสมาชิก คือ การเขียนแสดงคู่สมาชิกที่เกิดขึ้นด้วย มี 3 แบบ คือ
- a. แบบแจกแจงสมาชิกเป็นเซต
เช่น
a = {(1, 3), (2, 6), (3, 9), (4, 12), (5, 15), (6, 18), (7, 21), (8, 24), (9, 27)}
b. แบบแจกแจงสมาชิกแบบตาราง
เช่น
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
a(x) |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
c. แบบแจกแจงสมาชิกเป็นแผนภาพการจับคู่
เช่น
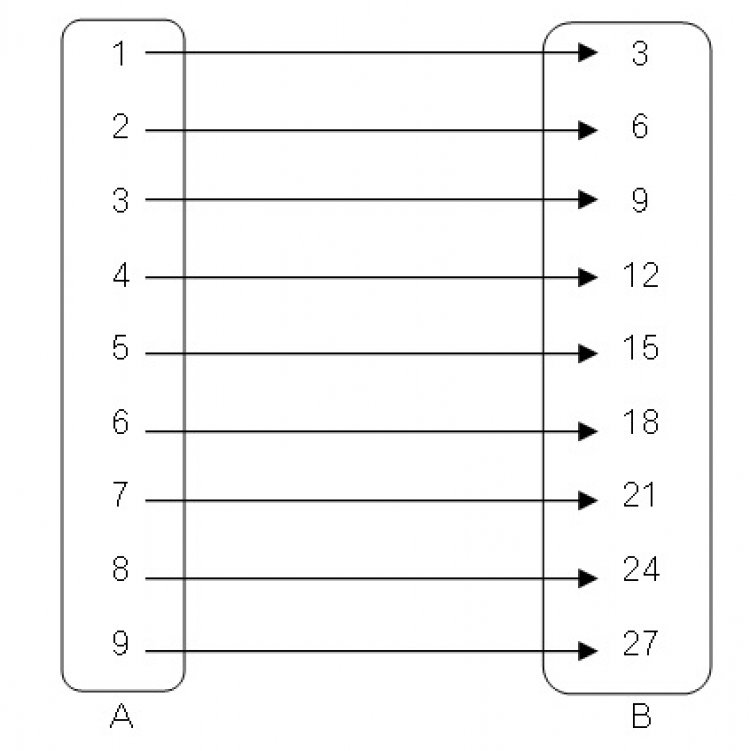
2. การเขียนลำดับแบบแจกแจงสมาชิกลำดับที่ 2
เป็นการนำสมาชิกตัวที่ 2 (a(x)) มาจัดเรียงตามแต่ละคู่ลำดับ
เช่น a(n) = {(1, 3), (2, 6), (3, 9), …, (n, a(n)}
เขียนเป็น a(n) = { 3, 6, 9, …, a(n)}
หมายเหตุ ถ้า a เป็นลำดับอนันต์ ต้องเขียนเป็น a(n) = { 3, 6, 9, …, a(n), … }
3. การเขียนลำดับแบบบอกเงื่อนไข
จะอยู่ในรูป an = เทอมของ n
เช่น an = n5 เราจะต้องทราบว่า
พจน์ที่ 1 ของลำดับ a1 = 15 = 1
พจน์ที่ 2 ของลำดับ a1 = 25 = 32 ไปเรื่อยๆ
ดังนั้น an = n5 สามารถเขียนได้เป็น 1, 32, 243, …, n5, …
หมายเหตุ
ถ้า a เป็นลำดับอนันต์ จะต้องเขียนเงื่อนไข an = เทอมของ n เสมอ
ถ้า a เป็นลำดับจำกัด จะเขียนหรือไม่ก็ได้
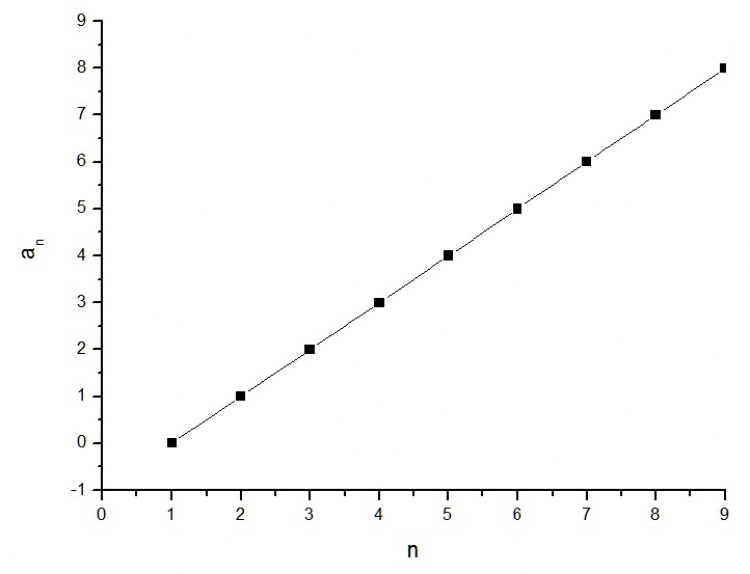
4. การเขียนลำดับแบบกราฟ
การเขียนแบบกราฟจะเริ่มจาก a(1) เสมอ เนื่องจากโดเมนของลำดับจะต้องเริ่มจาก 1 เท่านั้น (ไม่ใช่ 0 เหมือนกราฟทั่วไป)
เช่น a(n) = n-1 จะได้ลำดับ
a = {(1, 0), (2, 1), (3, 2), (4, 3), …}
a = 0, 1, 2, 3, 4, 5, …, n-1, …
กลับไปที่เนื้อหา
ลำดับแบบบอกเงื่อนไข: ลำดับเลขคณิต
ลำดับเลขคณิต (Arithmetic Sequence)คือ ลำดับที่มีผลต่างร่วมเป็นค่าคงตัวค่าหนึ่ง
“ ผลต่างร่วม (Common Difference) คือ ผลต่างที่ได้จากการนำพจน์ที่ n+1 ลบด้วยพจน์ที่ n สำหรับทุกจำนวนเต็มบวก n ”
1. ถ้ากำหนดให้ d เป็น ผลต่างร่วม จะได้ว่า
d = an+1 - an
หรือ an+1 = an + d
2. ถ้ากำหนดให้ a1 เป็นพจน์ที่ 1 ของลำดับ และ d เป็นผลต่างร่วม เราจะสามารถเขียนพจน์อื่นๆ ได้ ดังนี้
a2 = a1 + d
a3 = a2 + d = (a1 + d) + d = a1 + 2d
a4 = a3 + d = (a2 + d) + d = (a1 + 2d) + d = a1 + 3d
an = an-1 + d = (a1 + (n-2)d) + d = a1 + (n-1)d
ดังนั้น จากข้อกำหนดทั้งสองข้างต้น เราจะได้ว่า
พจน์ทั่วไปของลำดับเลขคณิต คือ an = a1 + (n-1)d
เมื่อ an = พจน์ที่ n ของลำดับเลขคณิต
a1 = พจน์ที่ 1 ของลำดับเลขคณิต
d = ผลต่างร่วม
ตัวอย่างที่ 1 จงคำนวณหาพจน์ของลำดับเลขคณิต เมื่อ an = 225, a1 = 3 และ d = 2
วิธีทำ พจน์ทั่วไปของลำดับเลขคณิต
an = a1 + (n-1)d
แทนค่าจากโจทย์
225 = 3 + (n-1)2
225 = 3 + 2n – 2
2n = 224
n = 112
ฉะนั้น ลำดับนี้มีพจน์ 112 พจน์
ตัวอย่างที่ 2 ถ้าผลบวกเลขคณิตตั้งแต่พจน์ที่ 1 ถึง 11 คือ 77 และผลบวกของกำลังสองของพจน์ที่ 4, 5, 6, 7, 8 คือ 285 จงหาลำดับนี้
วิธีทำ ปกติเราจะเขียนลำดับเลขคณิตแบบ
a1, a1+d, a1+2d,…
ซึ่งทำให้ยากต่อการพิจารณาและแก้โจทย์
เขียนแบบใหม่ คือ
a1-2d a1, a1-d, a1, a1+d, a1+2d,…
จากโจทย์ กำหนดให้มี 11 พจน์ นั่นคือ จำนวนพจน์เป็นจำนวนคี่ ได้แก่
a1-5d a1, a1-4d, a1-3d, a1-2d, a1-d, a1, a1+d, a1+2d, a1+3d, a1+4d, a1+5d
เราจะได้ว่า พจน์ที่ 6 เป็นพจน์กลาง ซึ่งกำหนดให้เป็น a1
และให้ผลต่างร่วมเป็น d
ฉะนั้น จะได้สมการ
(a1-5d) + (a1-4d) + (a1-3d) + (a1-2d)
+ (a1-d) + a1 + (a1+d) + (a1+2d) +
(a1+3d) + (a1+4d) + (a1+5d) = 77
ดังนั้น 11a1 = 77
a1 = 7
และจากโจทย์ จะได้สมการ
(a1-2d)2 + (a1-d)2 + (a1)2 + (a1+d)2
+ (a1+2d)2 = 285
ดังนั้น d = +2 และ -2
นั่นคือ เราจะได้ลำดับเลขคณิตสองชุด ได้แก่
d = +2 ลำดับเลขคณิต คือ -3, -1, 1, 3, 5, …
d = -2 ลำดับเลขคณิต คือ 17, 15, 13, 11, 9, …
ตัวอย่างที่ 3 จงหาค่าของ k โดยที่รากของสมการ x3 + 3x2 - 6x + k = 0 เป็นลำดับเลขคณิต
วิธีทำ
จากสมการ เราจะทราบว่า รากของสมการนี้มีอยู่ 3 ตัว (เนื่องจากเป็นสมการกำลังสาม) และเป็นลำดับเลขคณิต
ซึ่งสมมติให้เป็น (a1-d), a1, (a1+d)
ดังนั้น สมการนี้ คือ
[x- (a1-d)] [x- a1] [x- (a1+d)] = 0
x3 – 3a1x2 + (3a12 – d2)x – (a13 – ad2) = 0
เมื่อเทียบกับสมการที่โจทย์ให้มา จะได้ว่า
3a1 = 3 ; a1 = -1
3a12 – d2 = -6 ; d2 = 9 ; d = 3
a13 – ad2 = k ; k = - 8
ฉะนั้น k = - 8
ตัวอย่างที่ 4 จงหาพจน์ 5 พจน์ของลำดับเลขคณิตที่อยู่ระหว่าง 5 และ 29
วิธีทำ
สมมติว่าลำดับเลขคณิตนี้มีอยู่ทั้งหมด 7 พจน์
โดยมี a1 = 5, a7 = 29
หาค่าของผลต่างร่วม จาก an = a1 + (n-1)d
ฉะนั้น29 = 5 + (7-1) d
d = (29 – 5) / 6
d = 4
ลำดับเลขคณิตนี้ คือ 5, 9 ,13, 17, 21 ,25, 29
และพจน์ 5 พจน์ที่อยู่ระหว่าง 5 และ 29 คือ 9 ,13, 17, 21 ,25
ตัวอย่างที่ 5 จงหาพจน์กลางของลำดับต่อไปนี้ เมื่อลำดับเลขคณิตมีอยู่ 3 พจน์
1. 3, x, 10
2. 5, x, 7
3. 11, x, 23
วิธีทำ
หลักในการหาพจน์กลางของลำดับเลขคณิตที่มี 3 พจน์คือการหาค่าเฉลี่ยของพจน์แรกและพจน์สุดท้าย นั่นคือ
1. x = (3 + 10) / 2 = 13/2
2. x = (5 + 7) / 2 =12/2 =6
3. x = (11 + 23) / 2 = 34/2 = 17
+++
7. ลิมิตของอนุกรม (Limit of Series)




กลับไปที่เนื้อหา
ลิมิตของลำดับ หมายถึงการพิจารณาลำดับที่ n ของลำดับอนันต์ เมื่อ n มีค่ามากขึ้นโดยไม่มีที่สิ้นสุด
ซึ่งลำดับที่จะนำมาพิจารณาต้องเป็นลำดับอนันต์เท่านั้น เขียนแทนด้วยสัญลักษณ์
![]()
โดยเรียก L ว่า ลิมิตของลำดับ (Limit of sequence)
การพิจารณาลิมิตของลำดับ
1. ถ้า n → ∞แล้วทำให้ an เข้าใกล้หรือเท่ากับจำนวนจริง L เพียงจำนวนเดียว
จะเรียกลำดับนั้นว่า ลำดับคอนเวอร์เจนต์ (convergent sequence)
และมีลิมิตเท่ากับค่า L หรือเรียกว่า ลำดับนั้นลู่เข้าสู่ค่า L
2. ถ้า n → ∞แล้ว an ไม่เข้าใกล้หรือไม่เท่ากับจำนวนจริงใดๆ
จะเรียกลำดับนั้นว่า ลำดับไดเวอร์เจนต์ (pergent sequence)
และเป็นลำดับที่ไม่มีลิมิต หรือเรียกว่า ลำดับนั้นลู่ออก
ลำดับคอนเวอร์เจนต์ (Convergent Sequence)
ข้อสังเกตในการพิจารณาการลู่เข้าของลำดับ จะพิจารณาจากกราฟ ดังนี้
1. ลำดับอนันต์ที่มีค่า an = L เช่น
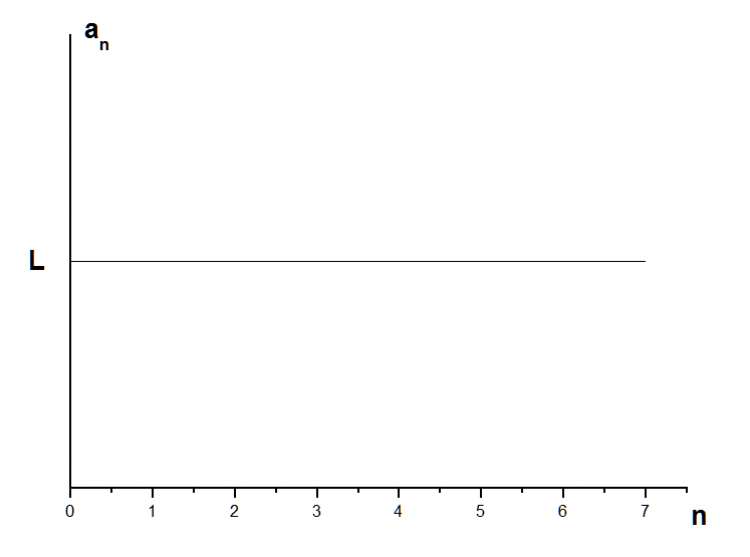
2. ลำดับอนันต์ที่จุด n → ∞ แล้ว an = L โค้งเข้าสู่เส้นตรงค่าหนึ่ง
2.1 n → ∞ แล้วทำให้ an มีค่าน้อยลง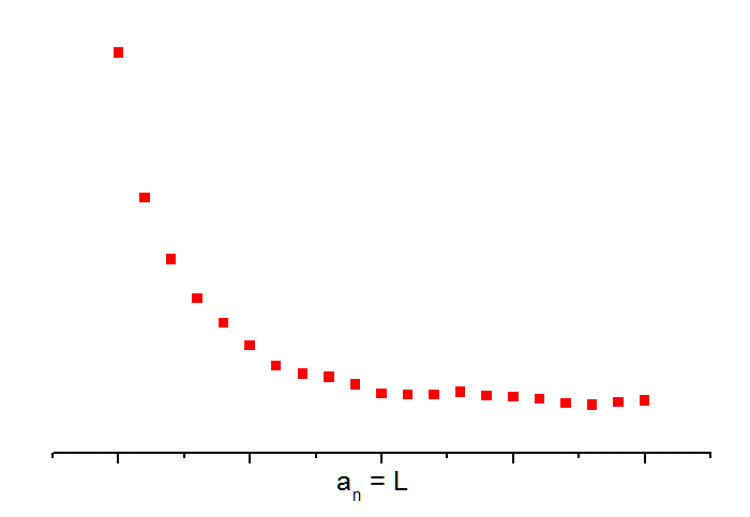
2.2 n → ∞ แล้วทำให้ an มีค่ามากขึ้น
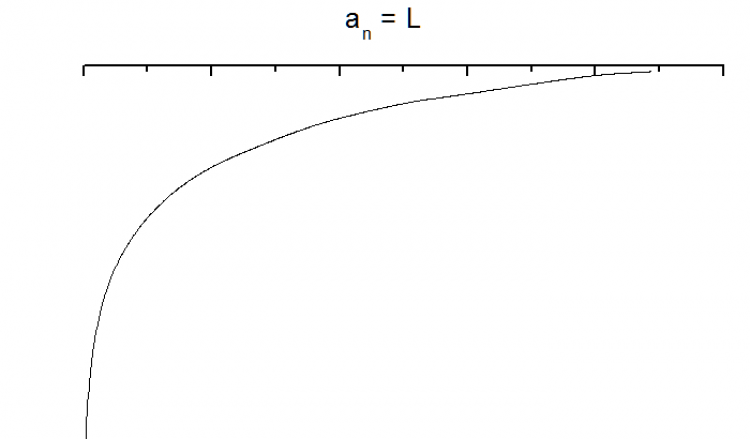
3. ลำดับอนันต์ที่จุด n → ∞ แล้ว an = L มีค่าแกว่งไปมาแต่ลู่เข้าสู่เส้นตรงค่าหนึ่ง
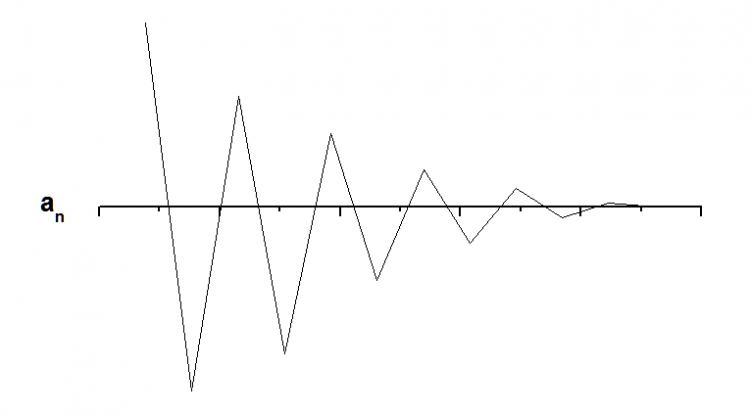
ลำดับไดเวอร์เจนต์ (pergent Sequence)
ลำดับไดเวอร์เจนต์ เป็นลำดับที่ไม่มีมิลิต ฉะนั้น ลักษณะของกราฟจะไม่วิ่งเข้าหาเส้นตรง
ที่เป็นจำนวนจริงใดๆ ได้แก่
1.ลำดับอนันต์ที่จุด n → ∞ แล้ว an พุ่งขึ้นหรือพุ่งลงอย่างไม่มีขอบเขต
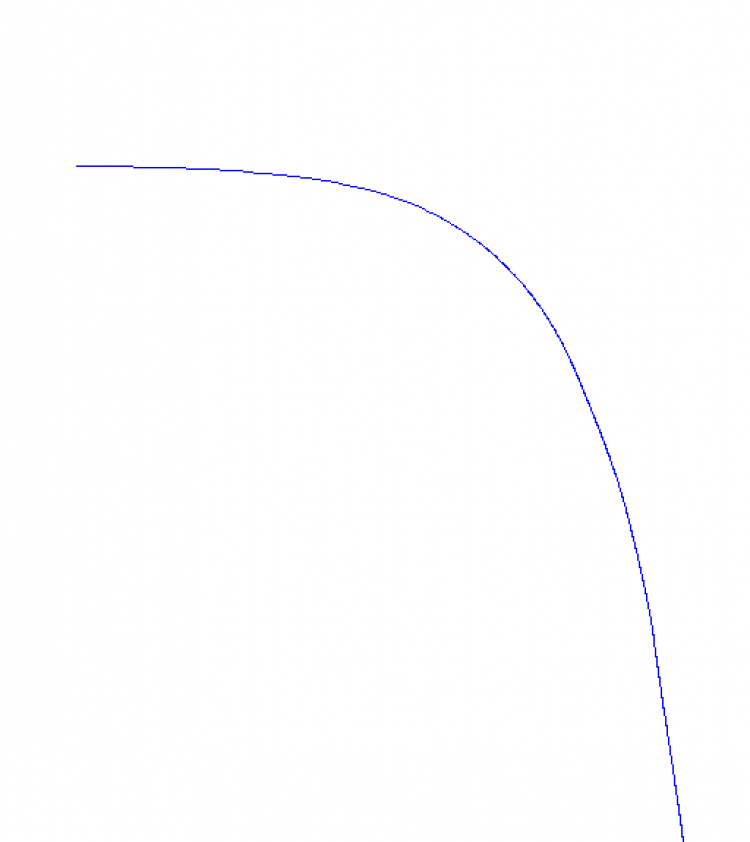
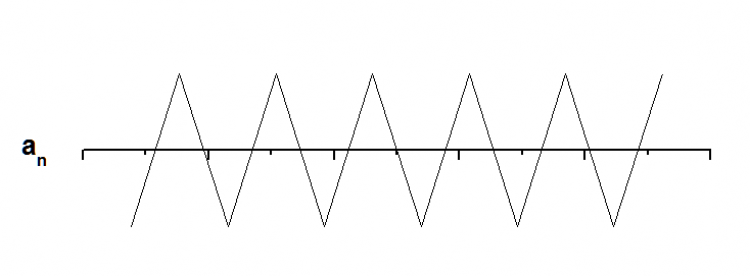
2.ลำดับอนันต์ที่จุด n → ∞ แล้ว an มีค่าแกว่งไปมาระหว่างจำนวนจริงมากกว่า 1 ค่า
ตัวอย่างที่ 1 จงพิจารณาว่า ลำดับ an = (-1)3n เป็นลำดับที่มีลิมิตหรือไม่
วิธีทำ
หาลำดับนี้ออกมาก่อน นั่นคือ -1, -1, -1, -1, ...
เขียนกราฟออกมา จะได้กราฟที่มีลักษณะ ดังนี้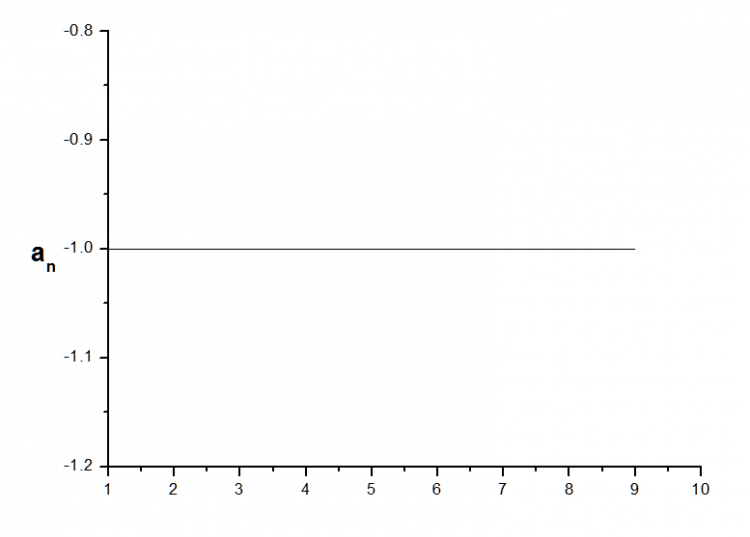
เราจะเห็นว่า เมื่อ n มีค่ามากขึ้น พจน์ที่ n ยังมีค่าเท่าเดิม
ฉะนั้น ลำดับนี้ เป็นลำดับคอนเวอร์เจนต์ที่ลู่เข้าสู่ -1
ตัวอย่างที่ 2 ลำดับ an = 3n-2 เป็นลำดับคอนเวอร์เจนต์หรือไดเวอร์เจนต์
วิธีทำ
ลำดับนี้ คือ 1, 4, 7, 10, 13, 16, 19, 22, ...
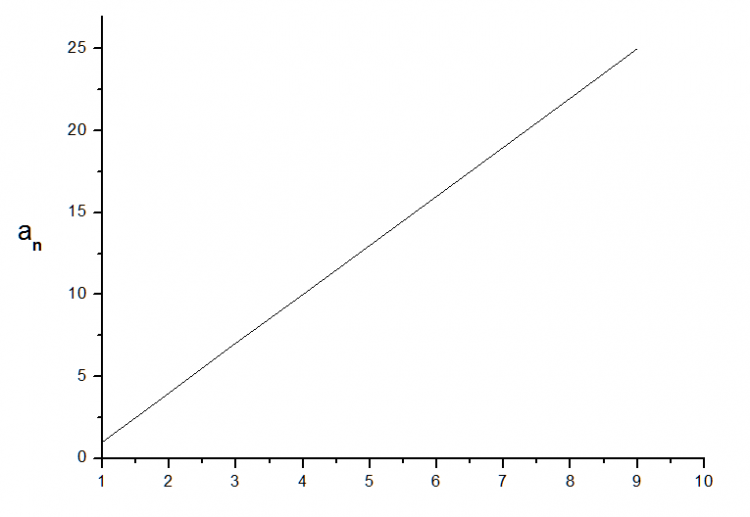
จากกราฟเราจะเห็นว่า พจน์ที่ n จะม่ค่าที่พุ่งขึ้นอย่างไม่มีขอบเขต
ฉะนั้น ลำดับนี้เป็นลำดับที่ไม่มีลิมิต หรือ ลำดับไดเวอร์เจนต์
การกระทำของพจน์
ซึ่งการกระทำของพจน์ใดๆ นั้น จะแบ่งออกเป็นการบวก ลบ คูณ และหารกันแบบพจน์ต่อพจน์
ดังนี้
1. การบวก ลบ
การบวกลบลำดับคอนเวอร์เจนต์ 2 ลำดับ จะได้ลำดับใหม่ที่เป็นลำดับคอนเวอร์เจนต์
และมีค่าลิมิตเท่ากับลิมิตของแต่ละลำดับมาบวกลบกัน
การบวกลบ ที่มีลำดับไดเวอร์เจนต์ร่วมด้วย อาจจะได้ลำดับที่เป็นคอนเวอร์เจนต์ หรือ ไดเวอร์เจนต์ก็ได้
2. การคูณ หาร
การคูณ หาร ลำดับคอนเวอร์เจนต์ 2 ลำดับ จะได้ลำดับใหม่ที่เป็นลำดับ คอนเวอร์เจนต์
การคูณ หาร ที่มีลำดับไดเวอร์เจนต์ร่วมด้วย อาจจะได้ลำดับใหม่ที่เป้นคอนเวอร์เจนต์หรือไดเวอร์เจนต์
ตัวอย่างที่ 3 ลำดับที่เกิดจากการบวกและลบ ลำดับต่อไปนี้
เป็นลำดับคอนเวอร์เจนต์หรือไดเวอร์เจนต์
1, 3, 5, 7, 9, ... และ 3, 5, 7, 9, 11, ...
วิธีทำ
จากการพิจารณาลำดับทั้งสอง จะพบว่า
1, 3, 5, 7, 9, ...เป็นลำดับไดเวอร์เจนต์
3, 5, 7, 9, 11, ...เป็นลำดับไดเวอร์เจนต์
เมื่อนำมาบวกกัน จะได้ 4, 8, 12, 16, ... เป็นลำดับไดเวอร์เจนต์
เมื่อนำมาลบกัน จะได้ -2, -2, -2, -2, ... เป็นลำดับคอนเวอร์เจนต์
ตัวอย่างที่4 ลำดับที่เกิดจากการคูณลำดับต่อไปนี้
เป็นลำดับคอนเวอร์เจนต์หรือไดเวอร์เจนต์
1. 1, 3, 5, 7, 9, ... และ 3, 5, 7, 9, 11, ...
2.1, -1, 1, -1, ...และ -2, 2, -2, 2, -2, ...
3. 1, 2, 3 ,4, ... และ 1, 1, 1, 1, ...
วิธีทำ
พิจารณาลำดับแต่ละลำดับก่อน
1. 1, 3, 5, 7, 9, ...ลำดับไดเวอร์เจนต์
และ 3, 5, 7, 9, 11, ... ลำดับไดเวอร์เจนต์
2.1, -1, 1, -1, ...ลำดับไดเวอร์เจนต์
และ -2, 2, -2, 2, -2, ... ลำดับไดเวอร์เจนต์
3. 1, 2, 3 ,4, ...ลำดับไดเวอร์เจนต์
และ 1, 1, 1, 1, ... ลำดับคอนเวอร์เจนต์
เมื่อนำมาคูณกันพจน์ต่อพจน์ จะได้ลำดับใหม่ ดังนี้
1.3, 15, 35, 63, 99, ...ลำดับไดเวอร์เจนต์
2.-2, -2, -2, -2, -2, ... ลำดับคอนเวอร์เจนต์
3. 1, 2, 3 ,4, ...ลำดับไดเวอร์เจนต์

กลับไปที่เนื้อหา
1.ลำดับฮาร์โมนิค (Harmonic Sequence)
ข้อกำหนดของลำดับฮาร์โมนิค คือ
ถ้ากำหนดให้ h1, h2, h3, …, hn ≠ 0 แล้ว 1/h1, 1/h2, 1/h3, …,
1/hn จะเป็นลำดับเลขคณิต
หรือ แต่ละพจน์ใดๆ ของลำดับฮาร์โมนิคเป็นส่วนกลับของลำดับเลขคณิต แต่ต้องมีเงื่อนไขว่า ลำดับนั้นต้องไม่เท่ากับ 0
ดังนั้น
พจน์ทั่วไปของลำดับฮาร์โมนิค คือ
hn = 1/an = 1 / a1 + (n-1)d
ตัวอย่างที่ 1 จงหาพจน์ที่ 63 ของลำดับ 1, ½, 1/3, ¼ , …
วิธีทำ
เริ่มจากการตรวจสอบลำดับก่อนว่า เป็นลำดับแบบใด
ถ้าทำให้เป็นส่วนกลับกัน จะได้ลำดับ 1, 2, 3, 4, … ซึ่งเป็นลำดับเลขคณิต
ดังนั้น เราสามารถบอกได้ว่า ลำดับข้างต้น เป็นลำดับฮาร์โมนิค
ถ้าต้องการหาพจน์ที่ 63 ของลำดับ จะสามารถหาได้จากการหาพจน์ที่ 63 ของลำดับเลขคณิตแทน ซึ่งจะง่ายกว่า นั่นคือ
an = a1 + (n-1)d
แทนค่าต่างๆ ของลำดับเลขคณิตลงไป
a63 = 1 + (63-1)1 = 63
พจน์ทั่วไปของลำดับฮาร์โมนิค คือ hn = 1/an
พจน์ที่ 63 ของลำดับฮาร์โมนิค ได้แก่ h63 = 1/63
2. ลำดับพหุนาม (Polynomail Sequence)
ข้อกำหนดของลำดับพหุนาม คือ
P(n) = aknk + ak-1nk-1 + … + a1n + a0
เมื่อ k เป็นจำนวนเต็มบวก และ ak, ak-1, …, a1, a0 เป็นจำนวนจริง
แล้ว ลำดับ an = P(n) เป็นลำดับพหุนาม
โดยทั่วไปแล้ว ถ้ามีการกำหนดลำดับพหุนามมาให้ เราจะสามารถเขียนลำดับออกมาได้โดยการแทนค่า n ลงไปใน an แต่ถ้ามีลำดับพหุนามมาให้ และให้หา an ค่อนข้างยาก แต่ถ้าเราดูจากผลต่างระหว่างลำดับ เราจะพบว่า ผลต่างของลำดับมีค่าไม่เท่ากัน แต่เราสามารถหาผลต่างของลำดับในแต่ละครั้งได้ จนกระทั่งได้ค่าผลต่างที่เป็นค่าคงที่ค่าหนึ่ง และแทนค่าที่ได้ลงในสมการของลำดับพหุนาม ดังนี้
an = a1 + ((n-1)/1)d1+ ((n-1)/2)d2 + ((n-1)/3)d3+ … + ((n-1)/k)dk
เมื่อa1 คือ พจน์ที่ 1
d1 คือ ผลต่างระหว่าง a2 กับ a1 หรือเท่ากับ (a2- a1)
d2 คือ ผลต่างของผลต่างสองตัวแรกจากการหาผลต่างครั้งที่ 1
d3 คือ ผลต่างของผลต่างสองตัวแรกจากการหาผลต่างครั้งที่ 2
dk คือ ผลต่างของผลต่างสองตัวแรกจากการหาผลต่างครั้งที่ k-1 (ค่าคงที่)
หมายเหตุ
(n-1)/r = [(n-1)*(n-2)*(n-3)* … * (n-r)] / [r*(r-1)*(r-2)* … * (3)*(2)*(1)]
อย่างที่ 2 จงหาพจน์ทั่วไปของลำดับ 2, 9, 28, 65, 126, …
วิธีทำ
หาค่าต่างๆ ดังนี้ 2 , 9 , 28 , 65 , 126 , …
7 19 37 61
12 18 24
6 6
จะได้ a1 = 2, d1 = 7, d2 = 19 – 7 = 12, d3 = 18 – 12 = 6
แทนค่าต่างๆ ลงในสมการเพื่อหาพจน์ที่ n
an = a1 + ((n-1)/1)d1+ ((n-1)/2)d2 + ((n-1)/3)d3
an = a1 + ((n-1)/1)d1+ [((n-1)(n-2))/2]d2 + [((n-1)(n-2)(n-3))/6]d3
an = 2 + ((n-1)/1)(7)+ [((n-1)(n-2))/2](12) + [((n-1)(n-2)(n-3))/6](6)
an = 2 + 7n – 7 + (n-1)(n-2)(6) + (n-1)(n-2)(n-3)
an = 7n – 5 + (n2-3n+2)(n+3)
an = n3+1
ดังนั้น พจน์ทั่วไปของลำดับนี้ คือ n3+1
ถ้าการหาผลต่างไปเรื่อยๆ แล้วพบว่า ได้ผลลัพธ์ที่เป็นลำดับเรขาคณิต เราจะได้สูตรในการหาพจน์ทั่วไป ดังนี้
an = Arn-1 + Bnk-1 + Cnk-2 + … + □nk-k
ตัวอย่างที่ 3 จงหาพจน์ทั่วไปของลำดับ 2, 5, 10, 19, 36, …
วิธีทำ
เริ่มจากหาค่าผลต่างของแต่ละพจน์ก่อน
2 , 5 , 10 , 19 , 36 , ……
3 5 9 17
2 4 8
จะพบว่าลำดับในขั้นตอนที่ k = 2 เป็นลำดับเรขาคณิต ที่มี r = 2
จากนั้นทำการแทนค่าต่างๆ ลงในสมการเพื่อหาพจน์ทั่วไปของลำดับ
จะได้ว่า
an = Arn-1 + Bnk-1 + Cnk-2 + … + □nk-k
an = A(2)n-1 + Bn2-1 + Cn2-2 มีแค่ 3 พจน์ เนื่องจาก k = 2
หาค่า A, B, และ C จากพจน์ที่ให้มา เนื่องจากตัวแปรมี 3 ตัว จึงต้องตั้งสมการ 3 สมการ ดังนี้
a1 = A(2)1-1 + B(1)2-1 + C(1)2-2 = A+B+C
A+B+C = 2---> 1
a2 = A(2)2-1 + B(2)2-1 + C(2)2-2 = 2A+2B+C
2A+2B+C = 5 ---> 2
A3 = A(2)3-1 + B(3)2-1 + C(3)2-2 = 4A+3B+C
4A+3B+C = 10---> 3
จากการแก้สมการทั้ง 3 จะได้ A = 2, B = 1 และ C = -1
ฉะนั้น เราจะได้พจน์ทั่วไปของลำดับนี้ ดังนี้
an = 2(2)n-1 + (1) n2-1 + (-1) n2-2
an = 2n+n-1
กลับไปที่เนื้อหา
ลำดับเรขาคณิต (Geometic Sequence)
จะแตกต่างกับลำดับเลขคณิตคือ เป็นลำดับที่มีอัตราส่วนร่วม (Common Ratio) คงที่ หมายถึง อัตราส่วนระหว่างพจน์ที่ n+1 กับพจน์ที่ n ทุกๆ คู่ จะมีค่าคงที่เสมอ
ถ้ากำหนดให้ r เป็นอัตราส่วนร่วม (Common Ratio)
จะได้ r = (an + 1) / (an)
หรือ an + 1 = an r
ถ้ากำหนดให้ a1 เป็นพจน์แรก และ r เป็นอัตราส่วนร่วม เราจะสามารถเขียนพจน์อื่นๆ ได้ดังนี้
a1 = a1
a2 = a1r
a3 = a2r = (a1r)r = a1r2
a4 = a3r = (a2r)r = (a1rr)r = a1r3
an = an-1r = a1rn-1
ดังนั้น เราจะสามารถหาพจน์ทั่วไปของลำดับเรขาคณิตได้จาก
an = a1rn-1
เมื่อ an คือ พจน์ที่ n ของลำดับเรขาคณิต
a1 คือ พจน์ที่ 1 ของลำดับเรขาคณิต
r คือ อัตราส่วนร่วม (Common Ratio)
ตัวอย่างที่ 1 จงหาพจน์ทั่วไปของลำดับเรขาคณิต 2, 4, 8, …
วิธีทำ
จากโจทย์ a1 = 2
r = 2
และพจน์ทั่วไปของลำดับเรขาคณิต คือ an = a1rn-1
แทนค่าที่มี จะได้
an = 2(2)n-1
an = 2(2)n (2)-1
an = 2(2)n / 2
an = 2n
ฉะนั้น พจน์ทั่วไปของลำดับเรขาคณิต คือ an = 2n
ตัวอย่างที่ 2 จงหาพจน์สุดท้ายของลำดับเรขาคณิตที่มีพจน์แรก เท่ากับ 3 และมีอัตราส่วนร่วมเท่ากับ 2/3 และจำนวนพจน์เท่ากับ 8
วิธีทำ
จากโจทย์ เราจะได้ว่า an = a1rn-1
an = 3(2/3)8-1
an = 3(2/3)7
an = 27/36
an = 128 / 729
ดังนั้น พจน์สุดท้ายของลำดับเรขาคณิต คือ 128 / 729
ตัวอย่างที่ 3 จงหาอัตราส่วนร่วมของลำดับเรขาคณิตที่มีพจน์ที่ 9 เท่ากับ 1/1458 และพจน์ที่ 5 เท่ากับ 1/18
วิธีทำ
จากโจทย์ เราจะได้ว่าa9 / a5 = r(9-5)
(1/1458) / (1/18) = r4
1/81 = r4
r2 = ±1/9
r = ± 1/3
ดังนั้น อัตรส่วนร่วมของลำดับเรขาคณิต คือ ± 1/3
ตัวอย่างที่ 4 จงหาพจน์แรกของลำดับเรขาคณิตที่มีพจน์ที่ 4 เท่ากับ 9 และพจน์ที่ 9 เท่ากับ 2187
วิธีทำ
สมมติให้ลำดับเรขาคณิต คือ a1, a1r, a1r2, a1r3
ดังนั้นa4 = a1r3 = 9
a9 = a1r8 = 2187
และ a9 / a4 = a1r8 / a1r3 = 2187 / 9
ซึ่งจะได้ว่า r5 = 2187 / 9 = 243 = 35
r = 3
เราทราบแล้วว่า พจน์ที่ 4 หรือ a1r3 = 9
ดังนั้น เราจะสามารถหาค่า a1 ได้ นั่นคือ a1 = 9 / 33 = 1/3
และ ลำดับเรขาคณิต คือ 1/3, 1, 3, 9 …
ตัวอย่างที่ 5 จงแสดงว่าตัวกลางเรขาคณิตของลำดับเรขาคณิต a, b, c คือ b = (ac)1/2
วิธีทำ
อัตราส่วนร่วม r = b/a หรือ c/b
b/a = c/b
b2 = ac
ฉะนั้น b = (ac)1/2
กลับไปที่เนื้อหา









