ทฤษฎีกราฟเบื้องต้น
1. กราฟและส่วนประกอบของกราฟ
ทฤษฎีกราฟเบื้องต้น
1. กราฟและส่วนประกอบของกราฟ
ในชีวิตประจำวัน กิจกรรมที่คนเราทำอยู่เป็นประจำนั้น ก็เพื่อแก้ปัญหาที่เกิดขึ้นจริงในการดำเนินชีวิต หลายปัญหาสามารถสร้างแบบจำลองที่เหมาะสมแทนปัญหา ซึ่งทำให้ปัญหาเข้าใจได้ง่ายขึ้น แล้วแก้ปัญหาโดยการหาคำตอบจากแบบจำลอง จากนั้นจึงนำคำตอบที่ได้จากแบบจำลองมาอธิบายผลที่เกิดขึ้นจากปัญหาจริง ซึ่งปัญหาที่เราสามารถจำลองปัญหาโดยการใช้จุดและเส้น ช่วยในการแก้ปัญหาให้ง่ายขึ้น เป็นที่มาของทฤษฎีกราฟนั่นเอง และต่อจากนี้เราจะมาพูดกันถึงทฤษฎีที่ว่าด้วยจุดและเส้น แต่เนื่องด้วยเรื่องนี้เป็นเรื่องที่ใหม่ จึงจำเป็นที่จะต้องทำความเข้าใจกับนิยามต่าง ๆ
นิยามกราฟ G = (V(G),E(G)) ประกอบด้วย เซตจำกัด 2 เซต คือ
1. เซตที่ไม่เป็นเซตว่างของจุดยอด(Vertex) แทนด้วยสัญลักษณ์ V(G)
2. เซตของเส้นเชื่อม(Edge) ที่เชื่อมระหว่างจุดยอด แทนด้วยสัญลักษณ์ E(G)
จากบทนิยามให้สังเกตว่า กราฟ นั้นจะต้องประกอบด้วยจุดเสมอ แต่เส้นจะมีหรือไม่ก็ได้ นั่นคือ V(G)เสมอ แต่ E(G) สามารถเป็นเซตว่างได้
การเรียกชื่อของจุดยอดนั้น ให้เรียกจากสัญลักษณ์ที่กำกับจุดนั้นได้เลย ส่วนการเรียกชื่อของเส้นเชื่อม สามารถเรียกได้ 2 ลักษณะ คือ เรียกจากสัญลักษณ์ที่กำกับเส้นเชื่อมนั้นได้เลย หรือกรณีที่เส้นเชื่อมนั้นไม่มีสัญลักษณ์กำกับ ให้เรียกจากจุดยอดทั้งสองของเส้นเชื่อมนั้น ดังแสดงในตัวอย่าง
ตัวอย่างจงพิจารณาว่ารูป A, B และ C เป็นกราฟหรือไม่ เพราะเหตุใด
A เป็นกราฟเนื่องจากเซตของจุดยอดไม่เป็นเซตว่าง
B ไม่เป็นกราฟเนื่องจากเซตของจุดยอดเป็นเซตว่าง
C เป็นกราฟเนื่องจากเซตของจุดยอดไม่เป็นเซตว่าง
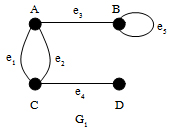
ตัวอย่างกำหนดกราฟ G1และ G2ดังรูป จงหาเซตของจุดยอด และเส้นเชื่อมของกราฟ จากกราฟที่กำหนดให้
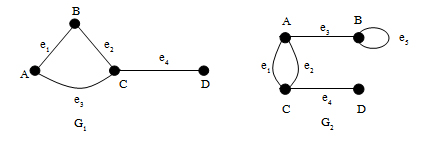
จากกราฟ G1ที่กำหนดให้ จะได้ว่า
V(G1) = {A, B, C, D}
E(G1) = {e1, e2, e3, e4} = {AB, BC, AC, CD}
จากกราฟ G2ที่กำหนดให้ จะได้ว่า
V(G2) = {A, B, C, D}
E(G2) = { e1, e2, e3, e4, e5}
จากกราฟ G2ของตัวอย่างที่ 2 จะสังเกตเห็นได้ว่า เส้นเชื่อม e1และ e2เป็นเส้นเชื่อมที่เชื่อมระหว่างจุดยอดคู่เดียวกัน คือ จุดยอด A และ C หากเราเรียกเส้นเชื่อม e1และ e2โดยอาศัยจุดยอดของเส้นเชื่อม จะพบว่าทั้งเส้นเชื่อม e1และ e2มีชื่อ AC เหมือนกัน ทำให้ไม่สามารถแยกเส้นเชื่อมทั้งสองออกจากกันได้ จึงสรุปได้ว่า การเรียกชื่อเส้นเชื่อมจากจุดยอดทั้งสองของเส้นเชื่อมนั้น ทำได้ในกรณีที่ระหว่างจุดยอดทั้งสองมีเส้นเชื่อมเพียงเส้นเดียวเท่านั้น
บทนิยามจุดยอด u และ v ของกราฟเป็นจุดยอดประชิด(Adjacent Vertices) ก็ต่อเมื่อ มีเส้นเชื่อมระหว่างจุดทั้งสอง และเราเรียกจุดยอด u และ v ว่าจุดปลาย(End Point) ของเส้นเชื่อมนั้น
เส้นเชื่อม e ของกราฟเกิดกับ(Incident) จุดยอด v ถ้าจุดยอด v เป็นจุดปลายจุดหนึ่งของเส้นเชื่อม e
ตัวอย่างจงแสดงว่าจุดยอดใดเป็นจุดยอดประชิด และเส้นเชื่อมแต่ละเส้นเชื่อมเกิดกับจุดยอดใด
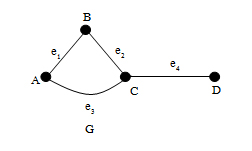
จุดยอด A และจุดยอด B เป็นจุดยอดประชิด
จุดยอด A และจุดยอด C เป็นจุดยอดประชิด
จุดยอด A และจุดยอด D ไม่เป็นจุดยอดประชิด
จุดยอด B และจุดยอด C เป็นจุดยอดประชิด
จุดยอด B และจุดยอด D ไม่เป็นจุดยอดประชิด
จุดยอด C และจุดยอด D เป็นจุดยอดประชิด
เส้นเชื่อม e1เกิดกับ จุดยอด A และ จุดยอด B
เส้นเชื่อม e2เกิดกับ จุดยอด B และ จุดยอด C
เส้นเชื่อม e3เกิดกับ จุดยอด A และ จุดยอด C
เส้นเชื่อม e4เกิดกับ จุดยอด C และ จุดยอด D
บทนิยามเส้นเชื่อมตั้งแต่ 2 เส้นเชื่อมที่เชื่อมระหว่างจุดยอดคู่เดียวกัน เรียกว่าเส้นเชื่อมขนาน(Parallel Edges)
เส้นเชื่อมที่เชื่อมจุดยอดเพียงจุดเดียว เรียกว่าวงวน(Loop)
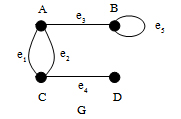
จากภาพจะพบว่า เส้นเชื่อม e1และ e2เชื่อมระหว่างจุดยอดคู่เดียวกัน คือ จุดยอด A และ C ดังนั้นจะได้ว่า e1และ e2เป็นเส้นเชื่อมขนานที่เกิดกับจุดยอด A และ C นอกจากนี้จะพบอีกว่า e5เป็นเส้นเชื่อมที่เชื่อมจุดยอด B เพียงจุดเดียว จึงเรียก e5ว่า วงวน
หมายเหตุ
Ü ในการเขียนแผนภาพของกราฟนั้น จะกำหนดตำแหน่งของจุดยอด ณ ตำแหน่งใดก็ได้ และจะลากเส้นเชื่อมของกราฟเป็นเส้นตรง หรือเส้นโค้ง มีความยาวเป็นเท่าใดก็ได้ โดยที่เส้นเชื่อมที่ลากจะไม่ตัดกับตัวมันเอง และไม่ลากผ่านจุดยอดที่ไม่ใช่จุดปลายของเส้นเชื่อมนั้น เช่น กราฟ G1และ G2ถือว่าเป็นกราฟเดียวกัน
Ü เส้นเชื่อมสองเส้นของกราฟ อาจลากตัดกันได้ โดยที่จุดตัดของเส้นเชื่อมทั้งสองไม่ถือว่าเป็นจุดยอดของกราฟ เช่น กราฟ G3และ G4ถือว่าเป็นกราฟเดียวกัน

กลับไปที่เนื้อหา
2. กราฟเชิงเดียว กราฟหลายเชิง และระดับขั้นของจุดยอด
บทนิยามกราฟเชิงเดียว(simple graph)คือ กราฟที่ไม่มีวงวน และไม่มีเส้นเชื่อมขนาน
กราฟหลายเชิง(multigraph)คือ กราฟที่มีวงวน หรือมีเส้นเชื่อมขนาน
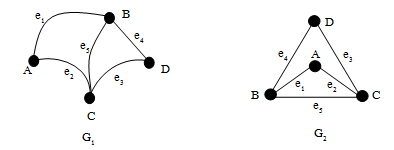
ตัวอย่างพิจารณากราฟต่อไปนี้ว่าเป็นกราฟเชิงเดียว หรือกราฟหลายเชิง เพราะเหตุใด
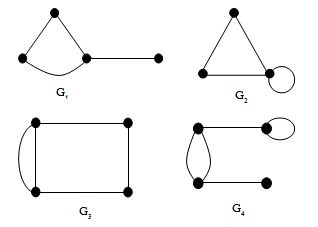
กราฟ G1เป็นกราฟเชิงเดียว
เพราะ ไม่มีทั้งวงวน และเส้นเชื่อมขนาน
กราฟ G2เป็นกราฟหลายเชิง
เพราะ มีวงวน
กราฟ G3เป็นกราฟหลายเชิง
เพราะ มีเส้นเชื่อมขนาน
กราฟ G4เป็นกราฟหลายเชิง
เพราะ มีทั้งวงวน และเส้นเชื่อมขนาน
บทนิยามให้ u เป็นจุดยอดในกราฟ G
ระดับขั้นของจุดยอด(Degree) ของจุดยอด u ในกราฟ G คือ จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด u เขียนแทนด้วย degG(u) หรือ deg u
1. เรียกจุดยอดที่มีระดับขั้นเป็น 0 ว่าจุดยอดเอกเทศ(Isolated Vertex)
2. เรียกจุดยอดที่มีระดับขั้นเป็น 1 ว่าจุดยอดปลาย(End Vertex)
3. เรียกจุดยอดที่มีระดับขั้นเป็นจำนวนคู่ ว่าจุดยอดคู่(Even Vertex)
4. เรียกจุดยอดที่มีระดับขั้นเป็นจำนวนคี่ ว่าจุดยอดคี่(Odd Vertex)
ตัวอย่างจงพิจารณาว่าจุดยอดแต่ละจุดยอดในกราฟมีระดับขั้นของจุดยอดเป็นเท่าใด และเป็นจุดยอดชนิดใด
พร้อมทั้งระบุระดับขั้นต่ำสุด และระดับขั้นสูงสุดของกราฟ G
จะเห็นได้ว่า เส้นเชื่อมที่เกิดกับจุดยอด A ได้แก่ เส้นเชื่อม e1, e2และ e3รวม 3 เส้น นั่นคือ จำนวนครั้งทั้งหมดที่เส้นเชื่อมเกิดกับจุดยอด A เป็น 3 สรุปได้ว่า ระดับขั้นของจุดยอด A เป็น 3
ในทำนองเดียวกัน เราสามารถหาระดับขั้นของจุดยอด C และ D ด้วยวิธีการเดียวกันนี้ ได้ผลเป็น 3 และ 1 ตามลำดับ
สำหรับจุดยอด B นั้น พบว่ามีทั้งเส้นเชื่อมธรรมดาและวงวน การนับดีกรีนั้นให้นับเส้นเชื่อมเป็น 1 และวงวน 2 ดังนั้นจุด B มีดีกรี 3
สังเกตง่ายๆว่า การนับดีกรีของจุดยอด มีวิธีง่ายๆคือ ลากวงกลมรอบจุดที่สนใจ แล้วนับจำนวนเส้นที่ออกจากจุดนั้น โดยไม่สนว่าเส้นนั้นจะเป็นเส้นเชื่อมธรรมดา หรือเส้นที่มาจากวงวน
ทฤษฎีบทต่อไปจะบอกถึงความสัมพันธ์ระหว่างดีกรีของจุดยอดกับจำนวนเส้นเชื่อม
ทฤษฎีบทที่1ให้ u1, u2, u3, …, u|V(G)|เป็นจุดยอดทั้งหมดในกราฟ G จะได้ว่า = 2|E(G)|
นั่นคือ ผลรวมของระดับขั้นของจุดยอดทุกจุดยอดในกราฟมีค่าเท่ากับ 2 เท่าของจำนวนเส้นเชื่อมในกราฟนั้น
ทฤษฎีบทที่ 2กราฟทุกกราฟมีจุดยอดคี่เป็นจำนวนคู่
กลับไปที่เนื้อหา
ตัวอย่างจงหาจำนวนเส้นเชื่อมของกราฟที่มีผลรวมของระดับขั้นของจุดยอดทุกจุดยอดในกราฟเท่ากับ 38
จากทฤษฎีบทที่ 1 คือ ผลรวมของระดับขั้นของจุดยอดทุกจุดยอดในกราฟมีค่าเท่ากับ 2 เท่าของจำนวนเส้นเชื่อมในกราฟนั้น
ให้ n เป็นจำนวนเส้นเชื่อมทั้งหมดของกราฟ
สามารถแปลงโจทย์เป็นสมการได้ดังนี้
38 = 2n
n = 19
กราฟมีเส้นเชื่อม 19 เส้นเชื่อม
ตัวอย่างที่จงหาจำนวนจุดยอดของกราฟที่มีเส้นเชื่อม 20 เส้น และมีจุดยอด 4 จุดยอดที่มีระดับขั้นของจุดยอด 3 ส่วนจุดยอดที่เหลือมีระดับขั้นของจุดยอด 4
ให้ n เป็นจำนวนจุดยอดทั้งหมดของกราฟ
ได้จำนวนจุดยอดที่มีระดับขั้นของจุดยอด 4 เป็น n-4
จากทฤษฎีบทที่ 1 คือ ผลรวมของระดับขั้นของจุดยอดทุกจุดยอดในกราฟมีค่าเท่ากับ 2 เท่าของจำนวนเส้นเชื่อมในกราฟนั้น
สามารถแปลงโจทย์เป็นสมการได้ดังนี้
(4)(3)+(n-4)(4) = 2(20)
12+4n-16 = 40
4n = 44
n = 11
จำนวนจุดยอดทั้งหมดของกราฟนี้ คือ 11 จุดยอด
บทนิยามให้กราฟ G = (V,E) มี V(G) = { u1, u2, u3, …, u|V(G)|} เรียก deg u1, deg u2, deg u3, …, deg u|V(G)|ว่าลำดับของระดับขั้น(Degree sequence) ของกราฟ G และถ้าลำดับของระดับขั้นดังกล่าว เป็นลำดับของระดับขั้นของกราฟ เราจะเรียกลำดับของระดับขั้นนั้นว่าลำดับของระดับขั้นเชิงกราฟ(Graphic degree sequence)
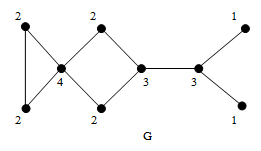
หมายเลขที่กำกับในแต่ละจุดยอดของ G แทนระดับขั้นของจุดยอดของแต่ละจุดยอด
เมื่อเรานำระดับขั้นของจุดยอดมาเขียนเป็นลำดับ เราอาจเขียนแทนได้ด้วยลำดับของระดับขั้น S1, S2และ S3ดังนี้
S1: 1, 1, 2, 2, 2, 2, 3, 3, 4
S2: 4, 3, 3, 2, 2, 2, 2, 1, 1
S3: 2, 1, 2, 3, 2, 4, 1, 3, 2
สังเกตว่าลำดับของระดับขั้น S1เป็นลำดับที่เรียงจากน้อยไปหามาก และ S2เป็นลำดับที่เรียงจากมากไปหาน้อย ส่วน S3เป็นลำดับที่ไม่ได้เรียง แต่ทั้งสามแบบล้วนแล้วแต่เป็นลำดับของระดับขั้นเชิงกราฟของกราฟ G ทั้งสิ้น โดยทั่วไปเราตกลงให้เรียงลำดับของระดับขั้นเชิงกราฟในแบบที่เป็นลำดับไม่เพิ่ม นั่นคือลำดับไม่เพิ่มซึ่งเป็นลำดับของระดับขั้นเชิงกราฟของกราฟ G ในที่นี้ คือ S2: 4, 3, 3, 2, 2, 2, 2, 1, 1
กลับไปที่เนื้อหา
4. กราฟเดียวกันและกราฟถอดแบบกัน
บทนิยามเรากล่าวว่า กราฟ G1และกราฟ G2เป็น กราฟถอดแบบกัน (Isomorphic) ก็ต่อเมื่อมีฟังก์ชัน ซึ่งเป็นฟังก์ชันหนึ่งต่อหนึ่งจาก V(G1) ไปทั่วถึง V(G2) โดยที่ uv E(G1) ก็ต่อเมื่อ (u) (v) E(G2) สำหรับทุก ๆ จุดยอด u และ จุดยอด v ใน G1และใช้สัญลักษณ์ G1G2แทน G1และ G2เป็น กราฟถอดแบบกัน
เรากล่าวว่า กราฟ G1และกราฟ G2เป็น กราฟเดียวกัน (Identical) ก็ต่อเมื่อ กราฟ G1และ G2เป็นกราฟถอดแบบกัน ที่ เป็น Identical คือ (u) = u สำหรับทุกจุดยอด u ใน V(G1)
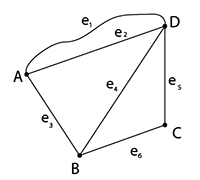
ตัวอย่างกราฟต่อไปนี้เป็นกราฟเดียวกันหรือกราฟถอดแบบกัน เพราะเหตุใด
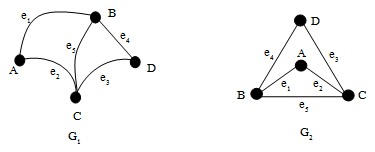
จะเห็นได้ว่ากราฟ G1และกราฟ G2มีเซตของจุดยอดเหมือนกัน คือ V(G1) = V(G2) = {A, B, C, D} และมีเซตของเส้นเชื่อมเหมือนกัน คือ E(G1) = E(G2) = {e1, e2, e3, e4, e5} โดยที่
เส้นเชื่อม e1เกิดกับ จุดยอด A และจุดยอด B
เส้นเชื่อม e2เกิดกับ จุดยอด A และจุดยอด C
เส้นเชื่อม e3เกิดกับ จุดยอด C และจุดยอด D
เส้นเชื่อม e4เกิดกับ จุดยอด B และจุดยอด D
เส้นเชื่อม e5เกิดกับ จุดยอด B และจุดยอด C
เหมือนกันทั้งหมด แม้นว่าจะมีลักษณะการวางตำแหน่ง และลักษณะเส้นเชื่อมที่แตกต่างกันก็ตาม
ดังนั้นกราฟ G1และกราฟ G2จึงเป็นกราฟเดียวกัน
ตัวอย่างกราฟต่อไปนี้เป็นกราฟเดียวกันหรือกราฟถอดแบบกัน เพราะเหตุใด
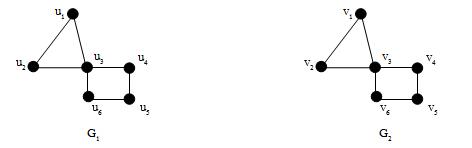
จะเห็นได้ว่ากราฟ G1และกราฟ G2ดูผ่าน ๆ เหมือนจะเป็นกราฟเดียวกัน มีจุดที่แตกต่างกันเพียงชื่อของจุดยอด ซึ่งมีฟังก์ชัน ซึ่งนิยามว่า (ui) = viโดยที่ i = 1, 2, 3, 4, 5, 6 ( (u1) = v1, (u2) = v2, (u3) = v3, (u4) = v4, (u5) = v5และ (u6) = v6) เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก V(G1) ไปทั่วถึง V(G2) โดยที่ โดยที่ uiujE(G1) ก็ต่อเมื่อ (ui) ( uj) = vivjE(G2) ดังนั้น กราฟ G1และกราฟ G2จึงเป็นกราฟถอดแบบกัน
กลับไปที่เนื้อหา
5. กราฟย่อย
บทนิยามกราฟย่อย (Subgraph) ของกราฟ G คือ กราฟที่ประกอบด้วยจุดยอดและเส้นเชื่อมใน G กล่าวคือ
G2เป็นกราฟย่อยของกราฟ G1ถ้า V(G2) V(G1) และ E(G2) E(G1)
กราฟย่อย G2ของ G1จะเรียกว่า กราฟย่อยแท้ (proper subgraph) ถ้า V(G2) V(G1) หรือ
E (G2) E (G2)
กราฟย่อย G2ของ G1จะเรียกว่า กราฟย่อยแผ่ทั่ว (spanning subgraph) ถ้า V(G2) = V(G1)
กำหนดให้ U V(G2) จะได้ว่ากราฟย่อย G2ของ G1จะเรียกว่า กราฟย่อยที่ก่อกำเนิดด้วยเซตของจุดยอด U (subgraph induced by vertex set S) ถ้า V(G2) = U และ คู่จุดยอดใน G2ประชิดกัน เมื่อ คู่จุดยอดนั้นประชิดกันใน G1
กำหนดให้ X E(G2) จะได้ว่ากราฟย่อย G2ของ G1จะเรียกว่า กราฟย่อยที่ก่อกำเนิดด้วยเซตของเส้นเชื่อม X (subgraph induced by edge set X) ถ้า E(G2) = X และ จุดยอดของ G2คือ จุดยอดของ G1ที่เกิดกับเส้นเชื่อมใน X
ตัวอย่างกราฟต่อไปนี้ กราฟใดเป็นกราฟย่อยของกราฟ G บ้าง

V(G) = {A, B, C, D} E(G) = {AB, BC, CD, AD, BD}
V(G1) = {A, B, C, D} E(G1) = {AB, BC, BD} V(G1) V(G) E(G1) E(G)
V(G2) = {A, B, C, D} E(G2) = {AB, BC, CD, AD, AC} V(G1) V(G) E(G1) E(G)
V(G3) = {A, B, C, D} E(G3) = {BC, AD, BD} V(G1) V(G) E(G1) E(G)
V(G4) = {A, B, C, D} E(G4) = {AB, BC, CD, AD, BD} V(G1) V(G) E(G1) E(G)
V(G5) = {P, Q, R, S} E(G5) = {PQ, QR, PS} V(G1) V(G) E(G1) E(G)
กราฟ G1, G3และ G4เป็นกราฟย่อยของกราฟ G เพราะประกอบด้วยจุดยอดและเส้นเชื่อมใน G
สังเกตุว่า กราฟ G1และ G3เป็นกราฟย่อยแท้ของกราฟ G แต่ G4ไม่เป็นกราฟย่อยแท้ของกราฟ G
กราฟ G1, G3และ G4เป็นกราฟย่อยแผ่ทั่วของกราฟ G
กราฟ G4เป็นกราฟย่อยที่ก่อกำเนิดด้วยเซตของจุดยอด{A, B, C, D} ของกราฟ G
กราฟ G1เป็นกราฟย่อยที่ก่อกำเนิดด้วยเซตของเส้นเชื่อม{AB, BC, BD} ของกราฟ G
กราฟ G3เป็นกราฟย่อยที่ก่อกำเนิดด้วยเซตของเส้นเชื่อม {BC, AD, BD} ของกราฟ G
กราฟ G4เป็นกราฟย่อยที่ก่อกำเนิดด้วยเซตของเส้นเชื่อม {AB, BC, CD, AD, BD} ของกราฟ G
กลับไปที่เนื้อหา
6. กราฟเชื่อมโยงและกราฟออยเลอร์
พิจารณากราฟต่อไปนี้
................................................
จะเห็นว่า เราสามารถเดินทางจากจุด A ไปยังจุด C ได้หลายเส้นทาง เช่น
A ไป B ไป C เขียนเป็นลำดับได้ว่าA,e3,D,e6,C
A ไป D ไป C เขียนเป็นลำดับได้ว่า A,e2,D,e5,C
จะเห็นว่า การเดินทางจากจุด A ไปยังจุด C สามารถเขียนเป็นลำดับซึ่งประกอบด้วยจุดและเส้นได้หลายแบบ เรียกลำดับที่ประกอบด้วยจุดและเส้นนี้ว่าแนวเดิน (walk)
จากตัวอย่าง เป็นการเขียน แนวเดิน A-C
เราจะเรียก กราฟซึ่งทุกๆจุดยอดมีแนวเดินถึงกันว่ากราฟเชื่อมโยง (connected graph)
วงจร(circuit)คือ แนวเดินซึ่งเริ่มและจบที่จุดเดียวกัน โดยไม่ใช้เส้นเชื่อมซ้ำกัน
วงจรออยเลอร์ (Eulerian circuit)คือ วงจรซึ่งผ่านจุดยอดและเส้นเชื่อมทั้งหมดในกราฟ
กราฟออยเลอร์ (Eulerian graph)คือ กราฟที่หาวงจรออยเลอร์ได้
นั่นคือ กราฟออยเลอร์คือกราฟที่เราสามารถเดินทางจากจุดหนึ่งแล้วกลับมาจุดเดิมได้โดยไม่เดินซ้ำเส้นทางเดิม เหมือนกับปัญหาการลากเส้นให้ได้รูปตามต้องการโดยไม่ยกปากกาและไม่ลากซ้ำเส้นเดิม
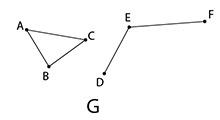
ตัวอย่างกราฟ G ต่อไปนี้เป็นกราฟเชื่อมโยงหรือไม่
................................................
.
ไม่เป็นกราฟเชื่อมโยง เนื่องจากไม่สามารถหาแนวเดินระหว่างจุดบางจุดได้ เช่น
ไม่สามารถหาแนวเดินระหว่าง B กับ E, D กับ F, C กับ F ได้
.
ตัวอย่างกราฟ G ต่อไปนี้เป็นกราฟเชื่อมโยงหรือไม่ และเป็นกราฟออยเลอร์หรือไม่
................................................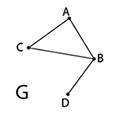
พิจารณาว่าเป็นกราฟเชื่อมโยงหรือไม่
แนวเดิน A-B คือ A,B
แนวเดิน A-C คือ A,C
แนวเดิน A-D คือ A,B,D
แนวเดิน B-C คือ B,C
แนวเดิน B-D คือ B,D
แนวเดิน C-D คือ C,B,D
จะเห็นว่า ทุกจุดมีแนวเดินเชื่อมถึงกัน ดังนั้น กราฟนี้เป็นกราฟเชื่อมโยง
สังเกตว่า การเขียนแนวเดินสำหรับกราฟนี้สามารถเขียนแค่จุดโดยไม่ต้องระบุเส้นเชื่อมได้ เพราะกราฟนี้ไม่มีเส้นเชื่อมที่เป็นวงวน หรือเส้นเชื่อมขนานที่จะทำให้เกิดความสับสนในการระบุเส้นเชื่อมระหว่างจุด
ต่อไปเราจะพิจารณาว่าเป็นกราฟออยเลอร์หรือไม่
จะเห็นว่า ไม่ว่าจะเริ่มเดินจากจุดใด จะต้องผ่านเส้นเชื่อมซ้ำอย่างน้อยหนึ่งเส้น จึงจะกลับไปจุดเดิมได้
ดังนั้นกราฟนี้ไม่มีวงจรออยเลอร์ และจึงไม่เป็นกราฟออยเลอร์
จากปัญหาการเดินทางผ่านทุกจุดและทุกเส้นทางโดยไม่ซ้ำเส้นทางเดิม ออยเลอร์ได้เสนอทฤษฎีบทว่า "กราฟใดก็ตามที่จะเป็นกราฟออยเลอร์ได้ กราฟนั้นจะต้องเป็นกราฟเชื่อมโยง ซึ่งทุกจุดยอดเป็นจุดยอดคู่"
จากตัวอย่างล่าสุด จะเห็นว่า มีเส้นเชื่อมออกจากจุด D เพียงเส้นเดียว จะได้ว่าจุด D เป็นจุดยอดคี่ ดังนั้นจึงไม่เป็นกราฟออยเลอร์
ตัวอย่างกราฟต่อไปนี้เป็นกราฟออยเลอร์หรือไม่
.
1. 2.
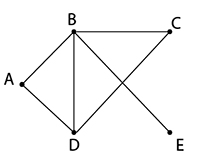
.
โดยทฤษฎีบทของออยเลอร์ เราจะได้ว่า
ข้อ 1 ไม่เป็นกราฟออยเลอร์ เนื่องจากมีจุดยอดคี่ ได้แก่ จุด D (ดีกรี 3) และ จุด E (ดีกรี 1)
ข้อ 2 ไม่เป็นกราฟออยเลอร์ เนื่องจากมีจุดยอดคี่ ได้แก่ จุด B (ดีกรี 3) และ จุด C (ดีกรี 5)
กลับไปที่เนื้อหา
7. สะพานเคอนิกส์แบร์ก
ปัญหาสะพานทั้งเจ็ดแห่งเมืองเคอนิกส์แบร์ก (Seven Bridges of Konigsberg) เป็นปัญหาทางคณิตศาสตร์ที่มีอายุเก่าแก่ โดยเลออนฮาร์ด ออยเลอร์ (Leonhard Euler) ได้เสนอคำตอบของปัญหานี้ไว้เมื่อปี 1735 และจากตรงนี้นำไปสู่จุดเริ่มต้นของการศึกษาทฤษฎีกราฟในวิชาคณิตศาสตร์
ปัญหานี้เริ่มขึ้นที่เมืองเคอนิกส์แบร์กในปรัสเซีย ซึ่งปัจจุบันคือ Kaliningrad ในประเทศรัสเซีย เรื่องมีอยู่ว่า สองข้างของแม่น้ำ Pregel มีเกาะอยู่ 2 เกาะ ซึ่งเชื่อมต่อกันด้วยสะพาน 7 แห่ง ดังรูป (สีเขียวคือสะพาน)
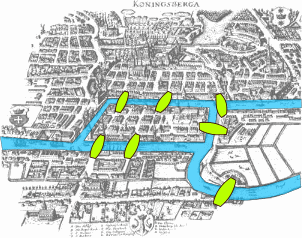
คำถามคือ เราสามารถเดินทางข้ามสะพานครบทั้ง 7 แห่งแล้วกลับมาจุดเริ่มต้นโดยไม่ข้ามสะพานซ้ำได้หรือไม่
ออยเลอร์ได้พิสูจน์ว่า คำตอบสำหรับคำถามนี้ืคือ เป็นไปไม่ได้ โดยได้แปลงปัญหาดังกล่าวให้เป็นกราฟ ให้จุดแทนแผ่นดิน และเส้นเชื่อมแทนสะพาน เราจะได้ทั้งหมด 4 จุดและ 7 เส้นเชื่อม ดังรูป

การจะแสดงว่าปัญหานี้เป็นไปไม่ได้ ก็คือแสดงว่า กราฟที่ได้นี้ไม่เป็นกราฟออยเลอร์นั่นเอง
โดยทฤษฎีบทของออยเลอร์ กราฟที่จะเป็นกราฟออยเลอร์ได้ ทุกๆจุดยอดต้องเป็นจุดยอดคู่ แต่จากกราฟจะเห็นว่า มีจุดยอดถึง 3 จุดที่มีดีกรี 3 และอีก 1 จุดที่มีดีกรี 5
ดังนั้นกราฟนี้ไม่เป็นกราฟออยเลอร์ ซึ่งหมายความว่า เราไม่สามารถเดินข้ามสะพานแล้วย้อนกลับมาจุดเริ่มต้นได้โดยไม่ข้ามสะพานซ้ำกันนั่นเอง
กลับไปที่เนื้อหา
8. กราฟถ่วงน้ำหนัก
ค่าน้ำหนัก (weight)คือ จำนวนจริงที่ไม่เป็นลบ ซึ่งกำหนดไว้บนเส้นเชื่อมของกราฟ
กราฟถ่วงน้ำหนัก (weighted graph)คือ กราฟที่ทุกเส้นเชื่อมมีค่าน้ำหนัก
ตัวอย่างกราฟต่อไปนี้เป็นกราฟถ่วงน้ำหนัก
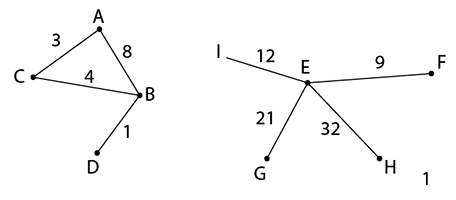
เราสามารถแปลงปัญหาในชีวิตจริงให้อยู่ในรูปตัวเลขเพื่อให้น้ำหนักกับแต่ละเส้นเชื่อมได้ เช่น ในชีวิตประจำวันเราอาจเดินทางจากจุดหนึ่งไปยังอีกจุดหนึ่งได้หลายเส้นทาง ซึ่งแต่ละเส้นทางก็จะมีมูลค่าที่ต้องจ่ายต่างกันไป ทั้งระยะเวลาที่ต้องใช้ ค่าใช้จ่ายที่ต้องใช้เพื่อเดินทางผ่านเส้นทางนั้น เป็นต้น
กราฟถ่วงน้ำหนักจะมีประโยชน์ในการหาเส้นทางที่สั้นที่สุดในการเดินทาง
กลับไปที่เนื้อหา
9. ต้นไม้แผ่ทั่วน้อยที่สุดและวิถีที่สั้นที่สุุด
ต้นไม้ (tree)คือ กราฟเชื่อมโยง ที่ไม่มีรูปปิด(หรือเรียกว่า วัฏจักร)
ต้นไม้แผ่ทั่ว (spanning tree)ต้นไม้ที่ใช้จุดยอดของกราฟครบทุถจุด
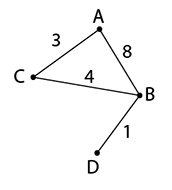
ตัวอย่างพิจารณากราฟต่อไปนี้
.........................................................
.
จากกราฟที่กำหนดให้ กราฟนี้ไม่เป็นต้นไม้ เนื่องจากมีสามเหลี่ยม ABC ซึ่งเป็นรูปปิด แต่กราฟนี้สามารถหาต้นไม้และต้นไม้แผ่ทั่วได้
เราสามารถหาต้นไม้แผ่ทั่วจากกราฟนี้ได้ทั้งหมดสามแบบ
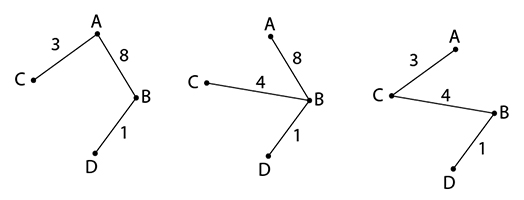
.
.
ข้อสังเกตต้นไม้เป็นกราฟเชิงเดียว ถ้ากราฟมีวงวนหรือมีเส้นเชื่อมขนาน กราฟนั้นจะไม่เป็นต้นไม้
ต้นไม้แผ่ทั่วที่มีจุดยอด n จุด จะมีเส้นเชื่อม n - 1 เส้น
.
ต้นไม้แผ่ทั่วที่น้อยที่สุด (minimum spanning tree)คือ ต้นไม้แผ่ทั่วที่มีผลรวมค่าน้ำหนักของแต่ละเส้นเชื่อมน้อยที่สุด
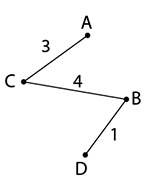
จากตัวอย่างข้างต้น จะเห็นได้ว่า ต้นไม้แผ่ทั่วที่น้อยที่สุด คือ
.........................................................
.
.
ซึ่งมีผลรวมค่าน้ำหนัก เท่ากับ 3 + 4 + 1 = 8
การหาต้นไม้แผ่ทั่วน้อยที่สุด จะมีประโยชน์ในการพิจารณาโครงสร้าง เช่น แผนผัง เพื่อให้ได้เส้นทางที่เชื่อมจุดทุกจุดโดยประหยัดค่าใช้จ่ายที่สุุด
วิธีการหาต้นไม้แผ่ทั่วน้อยที่สุด ทำได้โดยการเลือกเส้นเชื่อมจากกราฟที่กำหนดให้ทีละเส้น โดยเริ่มจากเส้นที่มีค่าน้ำหนักน้อยที่สุด และไม่เลือกเส้นที่ทำให้เกิดวัฏจักร
.
วิถี (path)คือ แนวเดินที่ไม่ซ้ำกับจุดยอดเดิม
วิถีที่สั้นที่สุด (shortest path)คือ วิถีที่ผลรวมค่าน้ำหนักน้อยที่สุด
.
ตัวอย่างจากกราฟ จงหาวิถีที่สั้นที่สุดจาก A ไป D
.........................................................
.
วิถี A-D มีทั้งหมดสองแบบคือ
A,B,D มีค่าน้ำหนัก 8 + 1 = 9
A,C,B,D มีค่าน้ำหนัก 3 + 4 + 1 = 8
ดังนั้น วิถีที่สั้นที่สุด คือA,C,B,D จะสังเกตว่า วิถีที่สั้นที่สุดไม่จำเป็นต้องเป็นวิถีที่มีจุดยอดน้อยที่สุด
กลับไปที่เนื้อหา



