พาไปดูข้อสอบคณิตฯ เด็กประถม (ระดับโลก) ปี 2540
- 1. Introduction
- 2. 2. ข้อสอบแข่งขันคณิตศาสตร์ประถมศึกษา ระดับโลก พ.ศ. 2540
- 3. 5. ข้อสอบแข่งขันคณิตศาสตร์ประถมศึกษา ระดับโลก พ.ศ. 2540
- 4. 6. ข้อสอบแข่งขันคณิตศาสตร์ประถมศึกษา ระดับโลก พ.ศ. 2540
- 5. 7. ข้อสอบแข่งขันคณิตศาสตร์ประถมศึกษา ระดับโลก พ.ศ. 2540
- 6. 8. ข้อสอบแข่งขันคณิตศาสตร์ประถมศึกษา ระดับโลก พ.ศ. 2540
- - All pages -
1. ข้อสอบแข่งขันคณิตศาสตร์ประถมศึกษา ระดับโลก พ.ศ. 2540
โจทย์ในการคูณกันตามรูปข้างล่างนี้
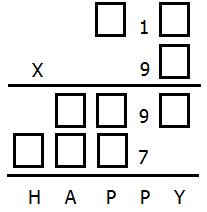
ตัวอักษรแต่ละตัวแทนเลขโดดที่แตกต่างกันส่วนช่องสี่เหลี่ยมแต่ละช่องแทนเลขโดดตัวใดก็ได้
ถามว่าจำนวน 5 หลักที่แทนด้วยตัวอักษร "H A P P Y" คือเลขอะไร?
แนวคิด
หลังจากอ่านโจทย์แล้วสตั๊นไปสามวิ (โอ้ว! ข้อสอบเด็กประถมหรือนี่ ^^') อย่างแรกต้องพิจารณาก่อนว่าโจทย์บอกอะไรเราบ้าง
เราทราบว่า ช่องสี่เหลี่ยมแทนตัวเลขอะไรก็ได้ที่เป็นเลขโดด (มีหลักเดียว) จะซ้ำหรือไม่ซ้ำกันก็ได้
ส่วน H A P P Y เป็นจำนวนๆหนึ่ง ซึ่งประกอบด้วยตัวเลข 5 หลัก แต่ละหลักเป็นเลขที่แตกต่างกัน ยกเว้นหลักสิบกับหลักร้อยที่เป็นตัวเลขตัวเดียวกัน
และเพราะกำหนดให้เลข ?1? คูณกับ 9? ดังนั้น H A P P Y จะต้องเป็นผลรวมของแถว 3 และ 4 (ดูรูปข้างล่างประกอบ)
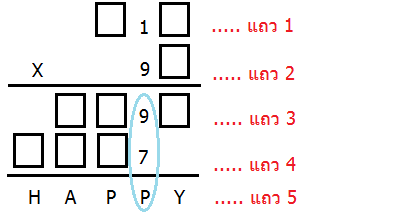
(พักถอนหายใจหนึ่งเฮือก... เฮ่ออ - -'' อะไรกันเนี่ย ทำยังไงต่อดีนะ)
ลองมองดูทั่วๆ เผื่อจะได้ไอเดียอะไรดีๆ มาแก้โจทย์ต่อ ลองดูเลข 9 กับ 7 ที่อยู่ในวงรีสีฟ้า จะเห็นได้ว่าเมื่อรวมกันแล้วให้ผลลัพธ์เป็น P
เราจึงได้ว่า 9 + 7 = 16 ซึ่งผลลัพธ์นี้จะเขียนไว้ในแถวที่ 5 (ตามหลักการบวก เมื่อผลเกิน 9 คือเป็น 10, 11, 12,...ขึ้นไป จะใส่หลักหน่วยแล้วทดไว้ในหลักถัดไปข้างหน้า) ดังนั้น P คือเลข 6 และทด 1 ในหลักร้อย แบบรูปข้างล่างนี้
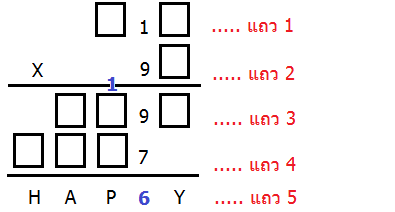
สิ่งที่พอจะช่วยเราได้เป็นอันดับต่อไป ก็คือเลข 7 ในแถวที่ 4 ซึ่งมันเป็นผลจากการคูณเลข 9 ในแถว 2 กับตัวเลขหลักหน่วยในแถว 1
9 คูณอะไรที่ให้ผลลัพธ์ลงท้ายด้วย 7 บ้างนะ?
91 = 9
92 = 18
93 = 27 <<< นี่ไง ลงท้ายด้วย "7"
94 = 36
95 = 45
96 = 54
97 = 63
98 = 72
99 = 81
910 = 90
จะเห็นได้ว่าเฉพาะเลข 3 เท่านั้นที่คูณกับ 9 แล้วให้ผลลัพธ์ลงท้ายด้วยเลข 7 ดังนั้นเราจึงพอจะเดาได้ว่า ตัวเลขในแถว 1 ควรจะลงท้ายด้วย 3 (สีเขียว)
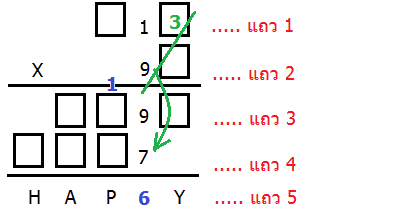
พอจะมีกำลังใจขึ้นมานิดนึงแล้วใช่ไหมคะ ^_^ เอานะ ต่อไปมาดูแถว 2 แล้วก็คิดต่อว่า 93 ได้ 27 ใส่ 7 ลงในแถว 4 (ขยับไปวางที่หลักสิบเพราะเป็นผลลัพธ์จากการคูณเลขหลักสิบ) ส่วนเลข 2 เก็บไว้ในใจ
กลับไปแถวที่ 2 ใหม่ จากนั้นเอา 91 ได้ 9 บวก 2 ที่เก็บไว้ในใจตะกี้ รวมเป็น 11 ก็ใส่ 1 ลงไป ทดหลักถัดไปอีก 1 (สีส้ม)
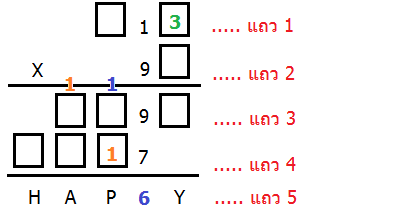
แต่หลักร้อยที่มีตัว P นั้น เราทราบแล้วว่า P=6 ดังนั้นหลักร้อยเสร็จเราแล้วค่ะ ;)
1+?+1 = 6 เพราะฉะนั้นจะได้ว่า ? = 4 เติมลงในสี่เหลี่ยมแถว 3 ได้แล้ว (สีม่วง)
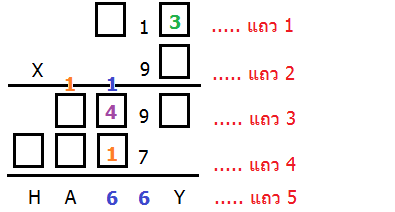
ต่อมา ถ้ามองไปที่ A น่าจะพอเดาได้ว่าตัวเลขที่ตรงหลักกัน จากแถว 3 และ 4 น่าจะทำให้เกิดผลลัพธ์การบวก เป็นเลขสองหลัก (เพราะต้องทดไปถึงหลักของ H ด้วย ไม่อย่างนั้น H ไม่เกิดแน่ๆ)
แต่หลังจากนี้ก็เหมือนจะมืดบอด... ช่องสี่เหลี่ยมยังมีว่างเยอะเหลือเกิน เราพอจะทำอะไรต่อได้อีกบ้าง
ลองกลับมาที่แถว 3 จะเห็นได้ว่าเลข 9 ในหลักสิบนั้นต้องได้มาจากหลักหน่วยในแถว 2 คูณกับหลักสิบในแถว 1 นั่นก็คือ ?1=9
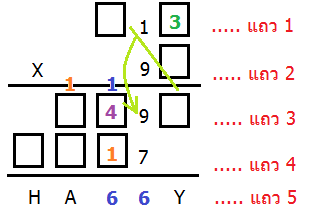
ง่ายที่สุดก็คงเป็น 91=9 แต่ถ้าลองเอา 9 ใส่ลงในหลักหน่วยของแถว 2 จะพบว่า
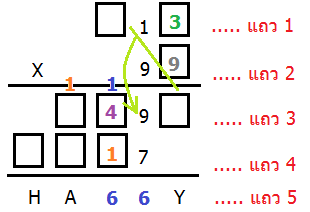
9 (หลักหน่วยแถว 2) 3 (หลักหน่วยแถว 1) เท่ากับ 27
ถ้าใส่ 7 ในหลักหน่วยของแถว 3 จะทำให้เหลือตัวทด 2
ต่อมา 9 (หลักหน่วยแถว 2) 1 (หลักสิบแถว 1) เท่ากับ 9 เมื่อรวมกับที่ทดไว้ 2 จึงเท่ากับ 11 แต่คำตอบนี้ไม่น่าจะถูกต้องเนื่องจากหลักสิบที่ตรงกันในแถว 3 นั้นจะต้องเป็นเลขที่ลงท้ายด้วย 9
สรุปว่าเลข 9 (สีเทา) ไม่ใช่ตัวเลขที่ถูกต้อง เริ่มคิดใหม่
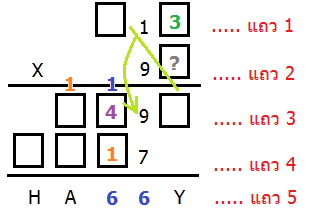
เป็นไปได้ว่า เลข 9 ที่เกิดในหลักสิบของแถว 3 เป็นตัวเลขที่รวมตัวทดไปด้วยแล้ว
เราทราบว่าหลักหน่วยในแถว 1 เป็นเลข 3 แน่ๆ
ดังนั้นเราจะต้องหาตัวเลขที่ตัวมันเองคูณ 3 (หลักหน่วยแถว 1) ได้คำตอบ แล้วเกิดการทดเลข ซึ่งเลขที่ทดนั้นเมื่อนำไปรวมกับ ตัวเลขนั้นคูณ 1 (หลักสิบแถว 1) แล้วจะได้เท่ากับ 9
สมมติว่าเป็น ? (หลักหน่วยแถว 2) 3 (หลักหน่วยแถว 1)
ถ้า ? เป็นเลข 1 จะได้ 13 = 3 ไม่เกิดการทด และไม่เพียงพอที่จะทำให้เกิดผลลัพธ์เลข 9 (หลักสิบ) ในแถว 3
ถ้า ?เป็นเลข 2 จะได้ 23 = 6 ไม่เกิดการทด และไม่เพียงพอที่จะทำให้เกิดผลลัพธ์เลข 9 (หลักสิบ) ในแถว 3
ถ้า ? เป็นเลข 3 จะได้ 33 = 9 ไม่เกิดการทด และไม่เพียงพอที่จะทำให้เกิดผลลัพธ์เลข 9 (หลักสิบ) ในแถว 3
ถ้า ?เป็นเลข 4 จะได้ 43 = 12 เกิดการทด แต่ยังไม่เพียงพอที่จะทำให้เกิดผลลัพธ์เลข 9 (หลักสิบ) ในแถว 3
ถ้า ? เป็นเลข 5 จะได้ 53 = 15 เกิดการทด แต่ยังไม่เพียงพอที่จะทำให้เกิดผลลัพธ์เลข 9 (หลักสิบ) ในแถว 3
ถ้า ? เป็นเลข 6 จะได้ 63 = 18 เกิดการทด แต่ยังไม่เพียงพอที่จะทำให้เกิดผลลัพธ์เลข 9 (หลักสิบ) ในแถว 3
ถ้า ? เป็นเลข 7 จะได้ 73 = 21 เกิดการทด (เลข 2 สีเทา) และดูเหมือนจะดีด้วย
เพราะทำให้ได้ผลลัพธ์เป็นเลข 9 ในหลักสิบของแถว 3 ดังภาพข้างล่างนี้
แล้วถ้า ? เป็นเลข 8 หรือ 9 ล่ะ ลองแทนดูก็จะเห็นว่าแม้จะเกิดการทด แต่ผลลัพธ์ในหลักสิบของแถว 3 ก็ไม่เท่ากับ 9
เราจึงสรุปในขั้นนี้ได้ว่า ตัวเลขในแถว 2 เท่ากับ 97 และทำให้ได้ว่า Y=1 โดยอัตโนมัติ (เย่!!)
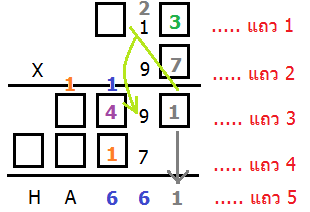
สรุปสิ่งที่เราได้ตอนนี้ เป็นดังภาพ
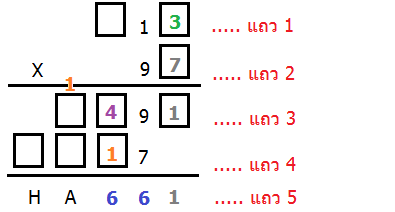
เหลือสี่เหลี่ยมปริศนาอีกเพียงแค่ 4 ช่องเท่านั้น!
มาดูต่อที่หลักร้อยของแถว 3 (เลข 4 สีม่วง) จะเห็นได้ว่ามันเป็นผลลัพธ์ของการคูณหลักหน่วย (เลข 7 แถว 2) กับหลักร้อย (? แถว 1)
7 คูณกับอะไร ถึงจะได้ผลลงท้ายด้วย 4 กันนะ
71= 7
72=14 << เข้าท่าอยู่ตัวเดียว
73=21
74=28
75=35
76=42
77=49
78=56
79=63
710=70
จากการคูณข้างบน จะเห็นได้ว่า เฉพาะ 72 เท่านั้นที่ให้ผลลัพธ์ลงท้ายด้วยเลข 4
เพราะฉะนั้น! เราจึงสรุปได้ว่าตัวเลขในแถว 1 เป็น 213 (ฮูเร่ร่ร่ ^O^/)
เมื่อเอา 21397 ตัวเลขที่ขาดหายไปจึงปรากฏครบ ดังภาพข้างล่าง
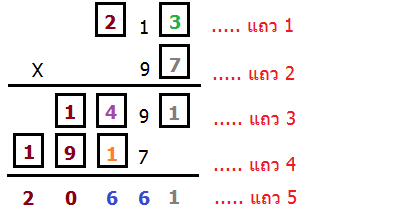
ดังนั้น จำนวน 5 หลักที่แทนด้วยตัวอักษรH A P P Yก็คือเลข2 0 6 6 1นั่นเอง Ans
หมายเหตุ: นี่เป็นเพียงข้อสอบข้อเดียวจากทั้งหมด 15 ข้อ น้องๆ ชั้นประถมที่ทำข้อนี้ได้นี่สุดยอดมาก และต้องทำเสร็จในเวลาที่กำหนดด้วย (แน่นอนว่าเป็นหลักนาที) เก่งจริงๆ
ขอบคุณโจทย์จาก
http://www.homebankstore.com/ebookfree3/009_Tiamsob/009%20%E0%B8%82%E0%B9%89%E0%B8%AD%E0%B8%AA%E0%B8%AD
%E0%B8%9A%E0%B8%84%E0%B8%93%E0%B8%B4%E0%B8%95%E0%B8%A8%E0%B8%B2%E0%B8%AA%E0%B8%95%E0%B8%A3
%E0%B9%8C%20%E0%B8%A1.%E0%B8%95%E0%B9%89%E0%B8%99%20%E0%B8%82%E0%B8%AD%E0%B8%87%E0%B8%9E%E0
%B8%A7%E0%B8%81%E0%B8%AA%E0%B8%A1%E0%B8%B2%E0%B8%84%E0%B8%A1%E0%B9%81%E0%B8%A5%E0%B8%B0%E0
%B8%81%E0%B9%89%E0%B8%AD%20%E0%B9%80%E0%B8%95%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%A1%E0%B8%AD
%E0%B8%94%E0%B8%A1%E0%B8%AF/World_HK_Person40.pdf
Return to contents
โจทย์จากรูปภาพทั้ง 3 รูปต่อไปนี้ แสดงถึงการชั่งน้ำหนักที่สมดุลกันของวัตถุรูปร่างต่างๆ โดยใช้ตาชั่งสองแขน
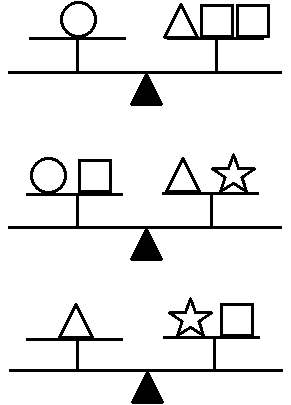
ถามว่าวัตถุรูปวงกลม
1 อัน มีน้ำหนักสมดุลกับวัตถุรูปสี่เหลี่ยม
กี่อัน
แนวคิด
โจทย์ข้อนี้ไม่ยากมากเมื่อเทียบกับข้อก่อนหน้านะคะ
สมมติกำหนดตัวเลขให้แต่ละกรณี ดังนี้
=
........... (1)
=
.............(2)
=.................(3)
เอาสามเหลี่ยมใน (3) ไปแทนใน (1) จะได้ว่า=................. (4)
และเมื่อดูดีๆ (2) นั้นคือการเติมเข้าไปฝากกับวงกลมใน (1) และเพื่อจะให้ตาชั่งสมดุล ก็ต้องใส่เข้าไปทั้งสองด้าน
ทำให้ จาก (4) เราสามารถวาดสมดุลของวัตถุได้เป็น=................. (5)
แต่ (2) เท่ากับ (5) คือ=
=
ซึ่งก็แสดงว่า=
แทนกลับเข้าไปใน (1) จึงได้เป็น=
สรุปว่า วงกลม1 อัน แทนสี่เหลี่ยม6 อัน Ans
ขอบคุณโจทย์จาก
http://www.homebankstore.com/ebookfree3/009_Tiamsob/009%20%E0%B8%82%E0%B9%89%E0%B8%AD%E0%B8%AA%E0%B8%AD
%E0%B8%9A%E0%B8%84%E0%B8%93%E0%B8%B4%E0%B8%95%E0%B8%A8%E0%B8%B2%E0%B8%AA%E0%B8%95%E0%B8%A3
%E0%B9%8C%20%E0%B8%A1.%E0%B8%95%E0%B9%89%E0%B8%99%20%E0%B8%82%E0%B8%AD%E0%B8%87%E0%B8%9E%E0
%B8%A7%E0%B8%81%E0%B8%AA%E0%B8%A1%E0%B8%B2%E0%B8%84%E0%B8%A1%E0%B9%81%E0%B8%A5%E0%B8%B0%E0
%B8%81%E0%B9%89%E0%B8%AD%20%E0%B9%80%E0%B8%95%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%A1%E0%B8%AD
%E0%B8%94%E0%B8%A1%E0%B8%AF/World_HK_Person40.pdf
Return to contents
โจทย์รถบรรทุกคันหนึ่งวิ่งจาก A ไป B ด้วยความเร็ว 50 กม./ชม. แล้ววิ่งกลับจาก B ไป A ด้วยความเร็ว 70 กม./ชม.
ถ้ารถคันนี้วิ่งไปและกลับแบบนี้เป็นจํานวน 3 รอบ โดยใช้เวลาทั้งสิ้น 18 ชั่วโมงถามว่า ระยะทางระหว่าง A กับ B เป็นกี่กิโลเมตร
แนวคิดสมมติว่าอ่านโจทย์แล้วยังงงว่าจะคิดอย่างไร แนะนำให้วาดภาพก่อนเลย เผื่อจะปิ๊งไอเดียดีๆ นะคะ
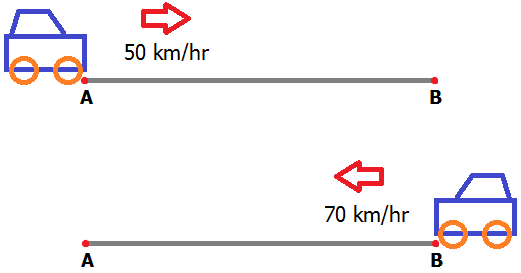
โจทย์บอกว่า ขาไป (A->B) รถวิ่งด้วยความเร็ว 50 กม./ชม.
ส่วนขากลับ (B->A) รถวิ่งด้วยความเร็ว 70 กม./ชม.
ปกติแล้วเมื่อเราพิจารณาเวลาที่ใช้ในการเดินทาง จะต้องดูความเร็วรถเป็นหลัก
อย่างที่ทราบว่าที่ระยะทางเท่ากัน รถที่วิ่งเร็วกว่าจะถึงที่หมายไวกว่ารถที่วิ่งช้า
ถ้าระยะทางจากต้นทางไปถึงปลายทาง 100 กม. รถวิ่งด้วยความเร็ว 100 กม./ชม. รถคันนี้จะถึงที่หมายในเวลา 1 ชม.
(เพราะดูจากความเร็วแล้ว แสดงว่าผ่านไป 1 ชม. รถจะวิ่งได้ 100 กม.)
ถ้ารถอีกคัน วิ่งเส้นทางนี้ แต่ใช้ความเร็วเพียง 50 กม./ชม. จะถึงจุดหมายช้ากว่า คือใช้เวลาในการเดินทาง 2 ชม.กว่าจะถึง
ดังนั้น
เราทราบจากโจทย์ว่า รถวิ่งไปกลับ 3 รอบ (วิ่งไป 3 ครั้ง และวิ่งกลับ 3 ครั้ง) ใช้เวลารวม 18 ชั่วโมง
และจาก
สมมติให้ระยะทางจาก A ถึง B เท่ากับ d
ดังนั้น เวลาที่รถใช้วิ่งขาไป =
และ เวลาที่รถใช้วิ่งขากลับ =
รวมเวลาที่ใช้ทั้งหมด 1 รอบ =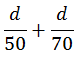
ถ้าวิ่งไปกลับ 3 รอบ (18 ชั่วโมง) จะใช้เวลาทั้งหมด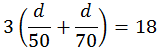
ถึงตรงนี้เราได้สมการแล้ว ก็แก้สมการเพื่อหาค่า d นะจ้ะ
นั่นก็คือ ระยะทางระหว่างจุด A และจุด B เท่ากับ 175 กม. ได้คำตอบแล้วAns
ลองคิดต่ออีกนิด (เช็คความถูกต้องของคำตอบไปด้วย) เราก็จะทราบเวลาที่ใช้ในการวิ่งรถขาไปและขากลับ
ระยะเวลาที่รถใช้ขาไป =
= 3.5 ชม.
ระยะเวลาที่รถใช้ขาไป =
= 2.5 ชม.
รวมไปกลับ 1 รอบใช้เวลา 3.5+2.5 = 6 ชม.
ดังนั้นวิ่งไปกลับ 3 รอบ จึงใช้เวลา 36 = 18 ชม. ถูกต้องตามที่โจทย์กำหนดมาจ้า
ขอบคุณโจทย์จาก
http://www.homebankstore.com/ebookfree3/009_Tiamsob/009%20%E0%B8%82%E0%B9%89%E0%B8%AD%E0%B8%AA%E0%B8%AD
%E0%B8%9A%E0%B8%84%E0%B8%93%E0%B8%B4%E0%B8%95%E0%B8%A8%E0%B8%B2%E0%B8%AA%E0%B8%95%E0%B8%A3
%E0%B9%8C%20%E0%B8%A1.%E0%B8%95%E0%B9%89%E0%B8%99%20%E0%B8%82%E0%B8%AD%E0%B8%87%E0%B8%9E%E0
%B8%A7%E0%B8%81%E0%B8%AA%E0%B8%A1%E0%B8%B2%E0%B8%84%E0%B8%A1%E0%B9%81%E0%B8%A5%E0%B8%B0%E0
%B8%81%E0%B9%89%E0%B8%AD%20%E0%B9%80%E0%B8%95%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%A1%E0%B8%AD
%E0%B8%94%E0%B8%A1%E0%B8%AF/World_HK_Person40.pdf
Return to contents
โจทย์ จงหาผลคูณ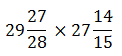
แนวคิด มีหลายวิธีที่จะหาคำตอบโจทย์ข้อนี้ ลองมาดูซัก 2 วิธีนะจ้ะ
วิธีแรก
(((กำลังอัพโหลดเนื้อหาบทเรียนนี้)))
วิธีที่สอง
Return to contents
โจทย์ปีเตอร์กำลังป่วยอยู่ เขาต้องกินยา A ทุกๆ 8 ชั่วโมง กินยา B ทุกๆ 5 ชั่วโมง กินยา C ทุกๆ 10 ชั่วโมง ถ้าเขากินยาทั้งสามชนิดพร้อมกัน เมื่อเวลา 7.00 น. ของวันอังคาร ถามว่า เมื่อไหร่เขาจะกินยาทั้งสามชนิดนี้พร้อมกันอีกครั้งหนึ่ง
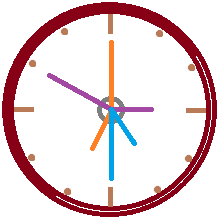
แนวคิด
เมื่ออ่านโจทย์แล้วลองคิดตาม จะพบว่า
ยา A จะถูกกินทุกๆ 8 ชม. ถ้าเริ่มกินเวลา 7.00 น.
ครั้งต่อไปคือ 7+8=15.00 น.
และครั้งต่อไปคือ 15+8=23.00 น.
และครั้งต่อไปคือ 23+8=31 หรือ 7.00 น.เช้าวันถัดไป (เวลาในหนึ่งวันจะจบลงที่ 24 ชม.หรือเที่ยงคืน ดังนั้นให้คิดถึงหน้าปัดนาฬิกาจริงๆ ว่า 8 ชม.นั้น ถ้าเริ่มนับจาก 23.00 น. ไป 1 ชม.ก็จะถึง 24.00 น. จากเราต้องนับชม.ต่อไปอีก 7 ชม.) และเป็นแบบนี้ไปเรื่อยๆ
ในลักษณะเดียวกัน ยา B จะถูกกินทุกๆ 5 ชม. นั่นคือ
ถ้าครั้งแรกเริ่มกินเวลา 7.00 น.
ครั้งต่อไปจะเป็น 7+5=12.00 น. (เที่ยงวัน)
และครั้งต่อไปจะเป็น 12+5=17.00 น.
และครั้งต่อไปจะเป็น 17+5=22.00 น.
เป็นแบบนี้ไปเรื่อยๆ
(นี่แค่ยา A กับ B ดูเหมือนปีเตอร์จะต้องกินยาบ่อยมากว่ามั้ยคะ ตั้งแต่ 7 โมงเช้า, เที่ยงวัน, บ่ายสาม, บ่ายห้าโมง, สี่ทุ่ม, ห้าทุ่ม, ตีสาม, ... กินบ่อยจังเนอะ ^^')
ว่ากันต่อ การกินยาทั้งสามชนิดนี้ จะต้องกินทุกๆ 8 ชม., 5 ชม. และ 10 ชม. ดูแล้วจะคล้ายกับว่า จำนวนชม.เหล่านี้วิ่งไล่กันอยู่บนหน้าปัดนาฬิกา และมันอาจจะมาพบพอดีกันเป๊ะที่เวลาๆหนึ่ง (และนี่คือสิ่งที่โจทย์ถาม)
ความรู้ที่เราจะเอามาแก้ปัญหานี้ ก็คือ การหาตัวเลขหนึ่งที่ใหญ่พอ ที่ทั้ง 8, 5, 10 จะค่อยๆสะสมจนไปถึงมัน (ในทางคณิตศาสตร์จะเรียกว่าเป็นตัวประกอบของมัน) แน่นอนนะคะว่าตัวเลขใหญ่ตัวที่ว่า น่าจะมีอยู่หลายตัว แต่เราจะมองหาตัวเลขที่น้อยที่สุด ซึ่งก็คือระยะเวลาที่น้อยที่สุดที่จะกินยาพร้อมกันทั้งสามชนิด และสิ่งที่จะช่วยเราได้ก็คือ เรื่อง ค.ร.น. (หาตัวเลขร่วม ที่ใหญ่พอ แต่น้อยที่สุดที่จะหาเจอ อย่าเพิ่งงงไปนะ)
หาค.ร.น.ด้วยวิธีตั้งหาร ได้เป็นดังนี้
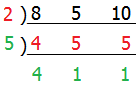
บรรทัดแรก พยายามหาตัวเลขเฉพาะที่หารเลขตัวตั้งสามตัวนั้นได้ลงตัว อย่างน้อยสองตัว (เพราะถ้าหารได้แค่ตัวเดียว แสดงว่าพอแล้ว หยุดทำได้)
ได้เลข 2 ( 2 หาร 8 กับ 10 ลงตัว) ผลลัพธ์คือ 4, 5, 5
จากนั้นบรรทัดต่อมา หาเลขเฉพาะที่หารผลลัพธ์ตะกี้ ได้ลงตัว อย่างน้อยสองตัว
ได้เลข 5 (5 หารเลขสีแดง 5 กับ 5 ลงตัว) ผลลัพธ์คือ 4, 1, 1
ถึงตอนนี้ เราเหลือ 4 ที่จะหารต่อเพียงตัวเดียว หยุดทำได้แล้ว
ทีนี้เอาเลขทุกตัวที่เป็นตัวหาร และผลลัพธ์ มาคูณกัน จะได้ ค.ร.น. = 2 5 4 1 1 = 40
เลข 40 ที่ได้นี้ก็เป็นจำนวนชั่วโมง ที่น้อยที่สุด ที่เลขสามตัว (8, 5, 10) จะวิ่งไปพบกันพอดีนั่นเอง
โจทย์กำหนดให้เวลาเริ่มต้นของการกินยา คือ 7.00 น. เช้าวันอังคาร
เวลาที่จะกินยาทั้งสามชนิดพร้อมกันนั้น จะนับจากนี้ไป 40 ชม.
คิดง่ายๆ ว่าจากนี้ไป 1 วัน (24 ชม.) จะเป็น 7.00 น. เช้าวันพุธ
และจากนี้ไป 2 วัน (48 ชม.) จะเป็น 7.00 น. เช้าวันพฤหัส
แต่ 48 เกินจาก 40 ไป 8 ชม. ดังนั้นนาฬิกาเดินถอยหลังลบออก 8 ชม. จะตรงกับ 23.00 น. (ห้าทุ่ม) ของวันพุธ
สรุปคือ ปีเตอร์จะกินยาพร้อมกันสามชนิด ตอน 23.00 น. ของวันพุธAns
หมายเหตุ:ที่จริงถ้าปีเตอร์ยังป่วยอยู่แบบนี้ไปนานๆ จำนวนชั่วโมงที่เขาจะกินยาทั้งสามชนิดพร้อมกัน นอกจาก 40 ชม.จากเวลาเริ่มต้น ยังเป็นไปได้อีกมากมายหลายค่าเลยนะคะ อย่างเช่น 80 ชม., 400 ชม., 800 ชม., ... เป็นต้น เราจึงเรียกเลขที่น้อยที่สุดในบรรดาตัวเลขเหล่านี้ ว่า "ค.ร.น." ซึ่งก็คือ "ตัวคูณร่วมที่น้อยที่สุด" ของตัวเลขที่เราสนใจ (กรณีนี้คือจำนวนชั่วโมง 8, 5, 10) จ้า
ขอบคุณโจทย์จาก
http://www.homebankstore.com/ebookfree3/009_Tiamsob/009%20%E0%B8%82%E0%B9%89%E0%B8%AD%E0%B8%AA%E0%B8%AD
%E0%B8%9A%E0%B8%84%E0%B8%93%E0%B8%B4%E0%B8%95%E0%B8%A8%E0%B8%B2%E0%B8%AA%E0%B8%95%E0%B8%A3
%E0%B9%8C%20%E0%B8%A1.%E0%B8%95%E0%B9%89%E0%B8%99%20%E0%B8%82%E0%B8%AD%E0%B8%87%E0%B8%9E%E0
%B8%A7%E0%B8%81%E0%B8%AA%E0%B8%A1%E0%B8%B2%E0%B8%84%E0%B8%A1%E0%B9%81%E0%B8%A5%E0%B8%B0%E0
%B8%81%E0%B9%89%E0%B8%AD%20%E0%B9%80%E0%B8%95%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%A1%E0%B8%AD
%E0%B8%94%E0%B8%A1%E0%B8%AF/World_HK_Person40.pdf
Return to contents
โจทย์ในชั้นเรียนหนึ่งมี 40% ของเด็กหญิง และ 50% ของเด็กชายที่ได้เกรด "A"ถ้ามีเด็กจำนวน 12 คนเท่านั้นที่ได้เกรด "A" และอัตราส่วนระหว่างจำนวนของเด็กหญิงกับเด็กชายในชั้นเท่ากับ 5:4 ถามว่า มีเด็กนักเรียนทั้งหมดในชั้นนี้กี่คน
แนวคิดโจทย์ไม่บอกว่าจำนวนเด็กหญิงและเด็กชายในห้องเรียนนี้เป็นเท่าใด ดังนั้นเราจึงใช้วิธีแก้ปัญหาแบบสมมติตัวแปรไม่ทราบค่า
กำหนดให้ จำนวนเด็กหญิง เป็น a
และ จำนวนเด็กชาย เป็น b
โจทย์ให้อัตราส่วน
นั่นก็คือ
จะได้ว่า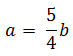
............................... (1)
40% ของเด็กหญิง + 50% ของเด็กชาย ที่ได้ "A" = เด็ก 12 คนเท่านั้นที่ได้ "A"
เขียนเป็นสมการได้เป็น
.............................. (2)
แทนค่า a ที่ได้จากสมการ (1) ลงในสมการ (2) เพื่อลดตัวแปร ทำให้การแก้สมการทำต่อไปได้
จะได้เป็น 
เพราะฉะนั้น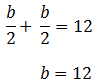
เมื่อได้ค่า b แล้ว แทนกลับในสมการ (1) ก็จะได้ค่า a
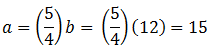
ดังนั้น จำนวนของเด็กหญิง (ค่า a) เท่ากับ 15 และจำนวนของเด็กชาย (ค่า b) เท่ากับ 12
เพราะฉะนั้น มีเด็กนักเรียนในชั้นเรียนนี้ทั้งหมด 15 + 12 = 27 คน Ans
เป็นไงบ้างคะ ข้อนี้ไม่ยากเกินไปใช่มั้ย ว่าแต่ใช้เวลาทำกันไปกี่นาทีเอ่ย อิอิ
ขอบคุณโจทย์จาก
http://www.homebankstore.com/ebookfree3/009_Tiamsob/009%20%E0%B8%82%E0%B9%89%E0%B8%AD%E0%B8%AA%E0%B8%AD
%E0%B8%9A%E0%B8%84%E0%B8%93%E0%B8%B4%E0%B8%95%E0%B8%A8%E0%B8%B2%E0%B8%AA%E0%B8%95%E0%B8%A3
%E0%B9%8C%20%E0%B8%A1.%E0%B8%95%E0%B9%89%E0%B8%99%20%E0%B8%82%E0%B8%AD%E0%B8%87%E0%B8%9E%E0
%B8%A7%E0%B8%81%E0%B8%AA%E0%B8%A1%E0%B8%B2%E0%B8%84%E0%B8%A1%E0%B9%81%E0%B8%A5%E0%B8%B0%E0
%B8%81%E0%B9%89%E0%B8%AD%20%E0%B9%80%E0%B8%95%E0%B8%A3%E0%B8%B5%E0%B8%A2%E0%B8%A1%E0%B8%AD
%E0%B8%94%E0%B8%A1%E0%B8%AF/World_HK_Person40.pdf
Return to contents
ม.5
ม.6
นักเรียน
