ทฤษฎีมูลฐานของเลขคณิต (Fundamental theorem of arithmetic)

        ในการเรียนระดับปฐมวัยเราได้เรียนรู้จำนวนชนิดต่าง ๆจากการนับ ต่อมาในระดับประถมศึกษามีการนำจำนวนนับเหล่านี้มาดำเนินการด้วยการบวก ลบ คูณ และหาร จนกระทั้งถึงระดับชั้นประถมศึกษาปีที่ 6 เราได้เรียนรู้เกี่ยวกับคุณสมบัติข้อหนึ่งของจำนวนนับคือการแยกตัวประกอบตัวอย่างเช่น 20=1X20=2X10=4X5 สังเกตว่า 20 เป็นจำนวนประกอบที่สามารถเขียนในรูปผลคูณของจำนวนนับได้หลายแบบแต่หากเราจะเขียน 20 ในรูปของผลคูณของจำนวนเฉพาะจะเห็นถึงคุณสมบัติของเลขคณิตข้อหนึ่งนั้นคือการเขียนในรูปผลคูณของจำนวนเฉพาะจะเขียนได้เพียงแบบเดียว 20= 2•2•5=2²•5 แน่นอนว่าจำนวนนับใดก็ตามย่อมสอดคล้องกับคุณสมบัติของเลขคณิตดังที่ยกตัวอย่างมาข้างต้นตามทฤษฎีบทมูลฐานของเลขคณิต

หลักการของทฤษฎีบทมูลฐานของเลขคณิต

       บทมูลฐานของเลขคณิตถูกกล่าวไว้ว่า “จำนวนเต็มใด ๆที่มากกว่า 1 จะสามารถแยกตัวประกอบในรูปผลคูณของจำนวนเฉพาะได้เพียงแบบเดียว”

       อาจกล่าวได้ว่าจำนวนเต็ม n > 1 สามารถเขียนในรูป

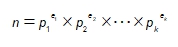
       ได้เพียงแบบเดียวเมื่อ เป็นจำนวนนับ p₁,p₂,…,p_k   เป็นจำนวนเฉพาะที่แตกต่างกัน และ e₁,e₂,…,e_k   เป็นจำนวนนับที่เป็นเลขชี้กำลังของ p₁,p₂,…,p_k   ตามลำดับในส่วนของบทพิสูจน์ผู้เขียนขอละไว้

ข้อสังเกต         1. จำนวนเฉพาะ p ใด ๆจะถูกเขียนในรูปp=p¹ เช่น13=13¹ 
                       2. จำนวนนับ 1 ไม่เป็นจำนวนเฉพาะเพราะถ้า 1 เป็นจำนวนเฉพาะแล้วจะเกิดข้อขัดแย้งกับทฤษฎีบทมูลฐานของเลขคณิตนั้นคือจำนวนนับใด ๆที่มากกว่า 1          สามารถเขียนในรูปผลคูณของจำนวนเฉพาะได้มากกว่า 1 แบบดังตัวอย่างที่จะอธิบายต่อไปนี้พิจารณา 20=2² X 5¹ แต่หากเรายอมรับว่า 1 เป็นจำนวนเฉพาะแล้ว 20=2²X5=1¹X2²X5¹=1²X2²X5¹=1³X2²X5¹= …. จะเห็นว่าเขียนได้มากมายนับไม่ถ้วน

การนำไปใช้

         ทฤษฎีบทมูลฐานของเลขคณิตได้ถูกนำไปใช้วิเคราะห์ สังเคราะห์ เพื่อหาคำตอบและยืนยันข้อเท็จจริงหลายปัญหาในคณิตศาสตร์ ผู้เขียนจะขอยกตัวอย่างบางกรณีเพื่อเป็นแนวทางให้ผู้อ่านได้ศึกษาและนำไปประยุกต์ใช้ต่อไป

การหาจำนวนตัวประกอบ

          ตัวประกอบจำนวนนับใด ๆคือจำนวนนับที่สามารถหารจำนวนนั้นได้ลงตัว หากพิจารณาถึงตัวประกอบของ 20 ย่อมหมายถึงจำนวนนับที่นำไปหาร 20 ได้ลงตัวได้แก่ 1,2,4,5,10 และ 20

ข้อสังเกต        

      1. จำนวนนับใด ๆจะมีตัวประกอบ 2 จำนวนที่เช่นได้แจ่มชัดคือ  และจำนวนนั้นเช่นตัวประกอบที่แจ่มชัดของ  คือ 1 และ 20

2. ผลหารของตัวประกอบจะเป็นตัวประกอบด้วยเช่น 2 เป็นตัวประกอบของ 20แล้วผลหาร 10 จะเป็นตัวประกอบของ 20 ด้วย

       จากตัวอย่างข้างต้นหากเขียน 20 ในตามหลักทฤษฎีบทมูลฐานของเลขคณิตจะได้ว่า 20 = 2X2X5=2²X5¹นั้นคือมีจำนวนเฉพาะที่เป็นตัวกำเนิด 20 คือ 2 ซึ่งมี 2 จำนวน และ 5 มี 1 จำนวนหากเราพิจารณาขั้นตอนการสร้างตัวประกอบจากการเลือก 2 และ 5 จะพบว่า

                     ขั้นตอนที่ 1 เลือก 2 ได้ 3 แบบคือเลือกมา 0, 1 และ 2 จำนวน

                     ขั้นตอนที่ 2 เลือก 5 ได้ 2 แบบคือเลือกมา 0, 1 จำนวน

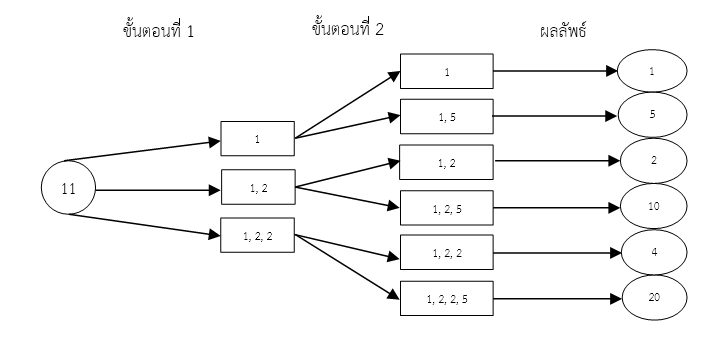
       จากขั้นตอนการทำงานจะเห็นว่าเราเลือก 2 ได้ 3 แบบในแต่ละแบบเลือก 5 ได้อีก 2 แบบจำนวนตัวประกอบของ 20 = 2² X 5¹ เท่ากับ (2+1)X(1+1) = 6 ในทำนองเดียวกันหาเราพิจารณา 144 = 2⁴ X 3² จะมีจำนวนตัวประกอบเท่ากับ (4+1) X (2 + 1) = 15 จำนวน

การหาห.ร.ม. และค.ร.น.

        จากความรู้เรื่องการแยกตัวประกอบเรารู้ว่าตัวหารที่หารได้ลงตัวคือตัวประกอบ ดังนั้นตัวหารร่วมมากจึงหมายถึงตัวประกอบร่วมที่มากที่สุดตัวอย่างเช่นจะหาห.ร.ม.ของ 120 และ 144 จากทฤษฎีมูลฐานของเลขคณิตจะได้ 120 = 2³ X 3¹ X 5¹ และ 144 = 2⁴ X 3² พิจารณา ห.ร.ม. จะได้ว่า ห.ร.ม.ของ 120 และ 144 คือ 2^min{3,4} X 3^min{1,2} X 5^min{0,1} =    2³ X 3¹ X 5⁰ = 24 และยังได้อีกว่า ค.ร.น.ของ 120 และ 144 คือ 2^max{3,4} X 3^max{1,2} X 5^max{0,1} =    2⁴ X 3² X 5¹ =720

        หมายเหตุ พิจาณา ห.ร.ม. ของ 504 630 756 จากทฤษฎีมูลฐานเลขคณิตจะได้ 504 = 2³ X 3² X 7   630 = 2 X 3² X 5 X 7 และ 756 = 2² X 3³ X 7 จะได้ว่า

ห.ร.ม.คือ 2^min{3,1,2} X 3^min{2,3,2} X 5^min{0,0,1} =    2¹ X 3² X 5⁰ X 7¹ = 126   ในทำนองเดียวกันจะได้ ค.ร.น. คือ 2^max{3,1,2} X 3^max{2,3,2} X 5^max{0,0,1} X 7^max{1,1,1} =    2³ X 3³ X 5¹ X7¹ =7,560

หาตัวคูณ n ที่น้อยที่สุดที่ทำให้ผลคูณเป็นจำนวนกำลังสอง

          พิจารณา 2⁵ X 3 X 5² X 7³ X n จะหาจำนวนนับ n ที่น้อยที่สุดที่ทำให้ 2⁵ X 3 X 5² X 7³ X n เป็นจำนวนกำลังสอง จะได้ว่า 2⁵ X 3 X 5² X 7³ X n = 2⁶ X 3² X 5² X7¹ = (2⁵ X 3 X 5² X7³ )X(2X3X7) นั้นคือ n = 42ในทำนองเดียวกันหากต้องการหาจำนวนนับ n ที่ทำให้ 2⁵ X 3 X 5² X 7³ X n เป็นจำนวนกำลังสามจะได้ว่า 2⁵ X 3 X 5² X 7³ X n = 2⁶ X 3³ X 5³ X7³ = (2⁵ X 3 X 5² X7³ )X(2X3²X5) นั้นคือ n = 90

หาเลขชี้กำลัง n ที่น้อยที่สุดที่ทำให้ผลบวก 2⁸ + 2¹¹ + 2ⁿ เป็นจำนวนกำลังสอง

          สมมติให้ 2⁸ + 2¹¹ + 2ⁿ = x² จะได้ว่า 48² + 2ⁿ = x²  พิจารณา 2ⁿ = x² - 48² = (x + 48) (x-48)

          จากทฤษฎีหลักมูลฐานของเลขคณิตจะได้ว่า (x + 48)(x-48)สามารถเขียนได้ในรูปของ 2ⁿ

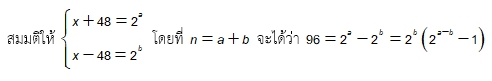
        จะเห็นว่า 2⁵ X 3 = 2^b X (2^a-b - 1) สรุปได้ว่า b=5 และ a-b = 2 ดังนั้น n=a+b=2+10=12

        การยืนยันหรือสรุปข้อเท็จจริงบางอย่าง

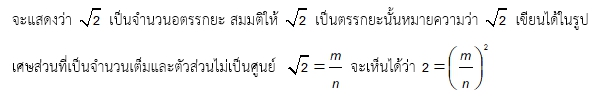
          จัดรูปจะได้ 2n² = m² ต่อไปเราจะแยกพิจารณาพจน์ทางซ้ายมือและพจน์ทางขวามือด้วยทฤษฎีบทมูลฐานของเลขคณิต

          พิจารณาพจน์ทางซ้ายมือ ถ้า n มีตัวประกอบ k จำนวนแล้ว 2n² จะมีตัวประกอบอยู่ 2k + 1 จำนวนซึ่งเป็นจำนวนคี่ แต่หาพิจารณาพจน์ทางขวามือคือ m² จะมีจำนวนตัวประกอบเป็นจำนวนคู่เสมอ จะเห็นว่าจำนวนตัวประกอบของพจน์ซ้ายมือจะถูกเขียนในรูปผลคูณที่มีจำนวนเฉพาะอยู่เป็นจำนวนคี่ในขณะที่พจน์ขวามือจะมีอยู่เป็นจำนวนคู่ ซึ่งขัดแย้งกับทฤษฎีบทมูลฐานของเลขคณิตที่กล่าวไว้ว่าจำนวนนับใด ๆจะสามารถเขียนในรูปผลคูณของจำนวนเฉพาจะได้เพียงแบบเดียว

บทสรุป

         ทฤษฎีหลักมูลฐานของเลขคณิตเป็นทฤษฎีที่ยืนยันว่าไม่ว่าเราจะทำการแยกตัวประกอบจำนวนนับใดๆ ก็ตามให้อยู่ในรูปผลคูณของจำนวนเฉพาะจะสามารถเขียนได้เพียงแบบเดียว จากหลักการดังกล่าวเราสามารถนำไปประยุกต์ใช้ในการหาจำนวนตัวประกอบของจำนวนนับใดๆ โดยพิจารณาจากเลขชี้กำลังของฐานที่เป็นจำนวนเฉพาะ นอกจากนี้ยังช่วยให้เราสามารถหา ห.ร.ม. และ ค.ร.น. ของจำนวนหลายๆ จำนวนได้โดยพิจารณาเลขชี้กำลังที่เป็น min และ max ของแต่ละฐาน ยิ่งไปกว่านั้นเมื่อมีจำนวนนับใดๆ ที่มีค่าเท่ากันเราจะได้ข้อค้นพบว่าจำนวนทั้งสองสามารถเขียนให้อยู่ในรูปของผลคูณของจำนวนเฉพาะในรูปแบบเดียวกัน จะเห็นว่าทฤษฎีหลักมูลฐานนั้นสามารถนำไปประยุกต์การแก้ปัญหาคณิตศาสตร์เพื่อให้ได้มาซึ่งข้อค้นพบ และข้อเท็จจริงดังที่ได้ยกตัวอย่างมาข้างต้น

 ตัวหารร่วมมาก (The Greatest Common Divisor)

         ก่อนเข้าสู่เนื้อหาผู้เขียนจะยกตัวอย่างปัญหาในชีวิตประจำวันที่เกี่ยวข้องกับตัวหารร่วมมากในการทำกิจกรรมแข่งขันกีฬาเชื่อมความสัมพันธ์ของนักเรียนโรงเรียนแห่งหนึ่งซึ่งมีนักเรียนจำนวน 2 ห้องโดยห้อง A มีนักเรียนจำนวน 20 คน และห้อง B มีนักเรียนจำนวน 24 คน ถ้าให้นักเรียนในแต่ละห้องจับกลุ่มกันเองโดยที่ทุกกลุ่มจะต้องมีจำนวนสมาชิกเท่ากันเพื่อมาแข่งขันกันผู้จัดควรจะให้นักเรียนแต่ละห้องจับกลุ่มกลุ่มละกี่คนเพื่อให้มีจำนวนกลุ่มผู้แข่งขันน้อยสุด ในปัญหานี้หาเราพิจารณาการแบ่งกลุ่มแต่ละห้อง

          ห้อง A สามารถแบ่งได้กลุ่มละ 1, 2, 4, 5, 10, 20

          ห้อง B สามารถแบ่งได้กลุ่มละ 1, 2, 3, 4, 6, 8, 12, 24

จะเห็นได้ว่าเราควรแบ่งเป็นกลุ่ม ๆ 4 คนซึ่งจะทำให้แต่ละกลุ่มของห้อง A และ ห้อง B มีสมาชิกเท่ากันโดยมีจำนวนกลุ่มทั้งหมด 11 กลุ่ม จากกระบวนการแก้ปัญหาข้างต้นจะเห็นว่าเรากำลังหาการแบ่งกลุ่มที่มากที่สุดโดยที่ทั้งสองห้องนั้นมีร่วมกัน (overlap) เราเรียกค่านี้ว่าตัวหารร่วมมาก

นิยามและความหมาย

หากเราพิจารณาปัญหาข้างต้นในเชิงคณิตศาสตร์จะพบว่าตัวหารของ 20 ซึ่งหมายถึงจำนวนที่สามารถหาร 20 ได้ลงตัวได้แก่ 1, 2, 4, 5, 10, 20 .ในขณะที่ตัวหารของ 24 ได้แก่ 1, 2, 3, 4, 6, 8, 12, 24 จะเห็นว่าตัวหารร่วมของ 20 และ 24 คือ 1, 2, 4 สังเกตว่าตัวหารร่วมที่มากที่สุดคือ 4 นั้นคือ 4 เป็น ห.ร.ม. ของ 20 และ 24 ดังนั้น ห.ร.ม. ของจำนวนตั้ง 2 จำนวนขึ้นไป สมมติให้ เป็น ห.ร.ม. และ แล้ว จะต้องสอดคล้องคุณสมบัติ 2 ข้อดังนี้

1. จะต้องเป็นตัวหารร่วมของ และ ( หาร ได้ลงตัว และ หาร ได้ลงตัว)
2. ไม่มีตัวหารร่วมใดมีค่ามากกว่า ห.ร.ม. (ถ้ามี ที่สามารถหาร และ b ได้ลงตัว )

วิธีการหาห.ร.ม.

          วิธีการหา ห.ร.ม.นั้นมีหลายวิธีแต่ละวิธีก็จะมีจุดแข็งและจุดอ่อนแตกต่างกัน ในบทเรียนนี้จะกล่าวถึงวิธีการหา ห.ร.ม. โดยนิยาม และระเบียบวิธียูคลิด

โดยนิยาม

          จากนิยามเราจะต้องหาจำนวนนับที่มากที่สุดสามารถหารจำนวนที่กำหนดให้ได้ลงตัวเช่น
ตัวอย่างที่ 1 จงหา ห.ร.ม.(81, 45)                                                                                                 

           จำนวนที่สามารถหาร 81 ได้ลงตัวคือ 1, 3, 9, 27, 81                                                        

           จำนวนที่สามารถหาร 45 ได้ลงตัวคือ 1, 3, 5, 9, 15, 45                                                 

           จะเห็นได้ว่า 9 เป็นจำนวนที่มากที่สุดที่หาร 81 และ 45 ได้ลงตัวดังนั้น ห.ร.ม.(81, 45) = 9

ตัวอย่างที่ 2 จงหา ห.ร.ม.(36, 90, 75)                                                                                  

           เราสามารถพิจารณา ห.ร.ม. ของแต่ละคู่จากนั้นนำ ห.ร.ม. ที่ได้ไปพิจารณากับจำนวนที่เหลือ                           

           ห.ร.ม.(36, 90,75) = ห.ร.ม.( ห.ร.ม.(36,90), 75 ) =ห.ร.ม. (18, 75) = 3

ตัวอย่างที่ 3 จงหา ห.ร.ม.(120, 216, 180, 224)
             ห.ร.ม.(120, 216, 180, 224) =ห.ร.ม.( ห.ร.ม.(120, 180), ห.ร.ม.(216, 224) ) = ห.ร.ม.(60, 8) = 4

ระเบียบวิธียูคลิด

         พิจารณา ห.ร.ม. ของจำนวน 2 จำนวนคือ a และ b โดยสมมติให้ a มีค่ามากกว่า b เมื่อนำ b ไปหาร a จะได้ค่าที่เป็นผลหารกำหนดให้เป็น q และเศษจากการหากำหนดให้เป็น r เราสามารถเขียนความสัมพันธ์ได้ดังสมการ   a = bq +r   แล้ว ห.ร.ม.(a, b) =ห.ร.ม.(b, r)

ตัวอย่างที่ 4 จงหา ห.ร.ม.(161, 207)

       ห.ร.ม.(207, 161)  = ห.ร.ม.(161, 46) = ห.ร.ม.(46, 23) = ห.ร.ม.(23,0) =23

ตัวอย่างที่ 5 จงหา ห.ร.ม.(4,131, 2,431)

ห.ร.ม.(4131, 2431) = ห.ร.ม. (2431, 1700) = ห.ร.ม. (1700, 731) 

                              = ห.ร.ม. (731, 238)      = ห.ร.ม. (238, 17)                                                           

                              = ห.ร.ม. (17, 0) = 17

จำนวนเฉพาะสัมพัทธ์

         ความสัมพันธ์รูปแบบหนึ่งของจำนวนนับสองจำนวนที่มีความสำคัญมากสำหรับศาสตร์ทางด้านคอมพิวเตอร์คือจำนวนสองจำนวนที่เป็นจำนวนเฉพาะต่อกัน หรือ เรียกว่าจำนวนเฉพาะสัมพัทธ์มีนิยามดังนี้

         จำนวนนับ m และ nจะเป็นจำนวนเฉพาะสัมพัทธ์ถ้า ห.ร.ม.(m,n) = 1  เราอาจจะคุ้นเคยกับแนวคิดเหล่านี้ในตอนที่เราเรียนเรื่องการลดทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำผ่านแนวคิดที่ว่าจำนวนตรรกยะบวกใด ๆสามารถเขียนในรูปเศษส่วนที่มีเศษและส่วนเป็นจำนวนนับโดยได้เพียงแบบเดียวคือเขียนในรูป m/n โดยที่ ห.ร.ม.(m,n) = 1 อาจจะกล่าวได้ว่าจำนวนตรรกยะบวกใด ๆสามารถเขียนในรูปของเศษส่วนอย่างต่ำได้เพียงแบบเดียว

         นอกจากนี้หลักการดังกล่าวยังถูกนำไปใช้ในการเข้ารหัส ถอดรหัส RSA โดยการเลือกกุญแจสาธารณะ public key เพื่อเข้ารหัสประกอบด้วยจำนวน 2 จำนวนคือ pq และ e ที่ซึ่ง p และ q เป็นจำนวนเฉพาะ และ e เป็นจำนวนเฉพาะสัมพัทธ์กับ (p-1)(q-1) ต่อมากำหนด private key เพื่อถอดรหัสโดยให้ เป็นตัวผกผันของ e ที่ลงรอยกับ(p-1)(q-1) อย่างไรก็ตามผู้เขียนขอละรายละเอียดเรื่องการเข้ารหัสและถอดรหัสแบบ RSA เนื่องจากผู้เรียนจะต้องมีความรู้ด้านทฤษฎีจำนวนในเชิงลึก

สรุป

          ในบทเรียนนี้ผู้เขียนได้อธิบายถึงแนวคิดของตัวหารร่วมมากซึ่งเป็นการอธิบายการจัดกลุ่มในแต่ละเซตตั้งแต่ 2 เซตขึ้นไปให้มีจำนวนสมาชิกมากที่สุด แนวคิดตัวหารร่วมมากในเชิงคณิตศาสตร์จึงประกอบด้วยคุณสมบัติ 2 ข้อคือ 1) ตัวหารร่วม และ 2) ตัวหารร่วมที่มากที่สุด นอกจากนี้ยังได้นำเสนอการหา ห.ร.ม. โดยนิยาม และระเบียบวิธียูคลิดซึ่งเหมาะตัวเลขที่มีค่ามาก และมีความซับซ้อนในการหาตัวหารโดยพิจารณา ห.ร.ม. ของตัวหารและเศษแทน และในส่วนสุดท้ายผู้เขียนได้กล่าวถึงประโยชน์ของ ห.ร.ม. ทั้งในเชิงคณิตศาสตร์ และการประยุกต์เพื่อให้ผู้อ่านเห็นถึงความสำคัญและประโยชน์ของคณิตศาสตร์ดังเช่นที่ ฮาร์ดี้ นักคณิตศาสตร์ชาวอังกฤษมีชีวิตในช่วง ค.ศ. 1877-1947 ได้เปรียบเปรยความงามของคณิตศาสตร์บริสุทธิ์นั้นเป็นศิลปะอย่างหนึ่ง และเขาก็ยังคงสนุกกับการศึกษาคณิตศาสตร์บริสุทธิ์ที่ไร้ประโยชน์

           ความรู้สึกของคนทั่วไปมักจะมองว่าคณิตศาสตร์เรียนไปก็ไม่ได้ใช้ประโยชน์รโดยเฉพาะอย่างยิ่งคณิตศาสตร์บริสุทธิ์ แต่ในความเป็นจริงมีทฤษฎีเกี่ยวกับจำนวนที่งดงาม และโดดเด่นเกินกว่าจะบรรยายถึงขอบเขตของมันได้ เราได้เห็นผลของทฤษฎีบทที่ขยายออกไปไกลเกินกว่าคำบัญญัติของทฤษฎี การอ่านรหัส RSA เป็นเพียงตัวอย่างเล็ก ๆตัวอย่างหนึ่งที่ชี้ให้เห็นถึงการประยุกต์กับวิทยาการคอมพิวเตอร์ นอกจากนี้ยังมีคณิตศาสตร์อีกหลายสาขาที่จำเป็นต้องใช้ในการพัฒนาระบบการอ่านรหัสเช่น พีชคณิตนามธรรม และ พีชคณิตเชิงเรขาคณิตเป็นต้น

 ตัวคูณร่วมน้อย (The least common multiple)

                ในชีวิตประจำวันของเราอาจจะมีปัญหาค.ร.น.แทรกอยู่ในปัญหาต่าง ๆโดยไม่รู้ตัวตัวอย่างเช่นในการจัดเซตอุปกรณ์อาบน้ำของโรงแรมแห่งหนึ่งประกอบด้วยสบู่ก้อน แชมพู และโฟมล้างหน้าชนิดซองโดยที่อุปกรณ์เหล่านี้ถูกจัดจำหน่ายเป็นแพ็ค แพ็คละ 15 20 และ 10 ซองตามลำดับ เราจะมีวิธีการสั่งอุปกรณ์ทั้งสามชนิดอย่างไรเพื่อให้สามารถจัดเป็นเซตอุปกรณ์อาบน้ำได้พอดี และจะได้อย่างน้อยที่สุดกี่เซต จะเห็นว่าหากเราสั่งสบู่ก้อน 4 แพ็ค แชมพู 3 แพ็ค และ โฟมล้างหน้า 10 แพ็คเราจะได้ของแต่ละอย่างจำนวน 60 ซองและสามารถจัดทั้งหมด 30 ชุดโดยไม่มีเศษเหลืออยู่เลย นั้นคือเราจะต้องเพิ่มจำนวนแพ็คของอุปกรณ์แต่ละชนิดไปจนกระทั้งได้จำนวนซองเท่ากัน ค่าน้อยที่สุดของจำนวนซองนี้เราเรียกว่าตัวคูณร่วมน้อย

การหาค.ร.น.

                จากตัวอย่างข้างต้นเราจะให้วิธีการคณิตศาสตร์เพื่อแสดงให้เห็นว่าค.ร.น. ของ 10 15 และ 20 คือ 60 ด้วยวิธีการจากนิยาม การตั้งหาร และทฤษฏีบท

การหาค.ร.น.โดยนิยาม

        นิยามของ ค.ร.น. หรือตัวคูณร่วมน้อย ภาษาอังกฤษให้อักษรย่อคือ lcm ย่อมาจากคำว่า least common multiple รากศัพท์คำว่า multi หมายถึงการเพิ่มซ้ำๆ หลายครั้งเรียกว่าตัวคูณ common หมายถึง มีร่วมกัน และ least หมายถึงน้อยที่สุด นิยามตัวคูณของ a จึงหมายถึงจำนวนที่ a หารได้ลงตัวดังนั้น

        ตัวคูณของ 10 คือ 10   20   30   40   50   60   70   80   90   100 120 …
        ตัวคูณของ 15 คือ 15   30   45   60   75   90   105 120 135 140 155 …
        ตัวคูณของ 20 คือ 20   40   60   80   100 120 140 160 180 200 220 …

        สังเกตว่าตัวคูณร่วมของ 10 15 และ 20 คือ 60, 120, 180, … ดังนั้นตัวคูณร่วมที่น้อยที่สุด ค.ร.น.(10,15,20) คือ 60 จากกระบวนการดังกล่าวเราสามารถให้นิยาม ค.ร.น. ในเชิงคณิตศาสตร์ได้ดังนี้

        สำหรับจำนวนนับ a และ b ใดๆ แล้ว d จะเป็น ค.ร.น.ของ a และ b ถ้าสอดคล้องคุณสมบัติ 2 ข้อต่อไปนี้

        m จะต้องเป็นตัวคูณร่วมของ a และ b ( a และ b จะต้องหาร m ได้ลงตัว ) ในบรรดาตัวคูณของ a และ b ทั้งหมด m จะต้องมีค่าน้อยที่สุด( ถ้า mเป็นตัวคูณร่วมค่าอื่นแล้ว m >= m)

การหาค.ร.น. โดยทฤษฎีบท

                ในตอนที่เราเรียนเรื่องการบวกลบเศษส่วนเราถูกสอนให้ทำตัวส่วนให้เท่ากันเช่นถ้าต้องการคำนวณ 3/5 + 1/20 เราจะต้องทำส่วนให้เท่ากันคือ 20 ต่อมาเมื่อเราพิจารณาปัญหา 3/18 + 1/12 เราถูกสอนให้แก้ปัญหานี้ด้วยการหา ค.ร.น. ของ 18 และ 12 เพื่อทำส่วนให้เท่ากัน จะเห็นว่าโจทย์ข้อแรกนั้นเราไม่จำเป็นต้องกล่าวถึง ค.ร.น. เนื่องจาก 20 เป็นตัวคูณร่วมของ 20 และ 5 และมีค่าน้อยที่สุดจากข้อสังเกตจึงสามารถสรุปเป็นทฤษฎีดังนี้

                ทฤษฎีบทที่ 1 ถ้า a หาร b ได้ลงตัวแล้ว lcm(a,b)=b

                สำหรับวิธีการหา ค.ร.น. เราคุ้นเคยการหาค.ร.น.ด้วยวิธีตั้งหารเป็นอย่างดีเช่น ค.ร.น.ของ 15 และ 20 คำนวณได้ดังนี้

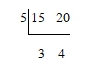
จะเห็นว่า ห.ร.ม. ของ 15 และ 20 คือ 5 (gcd(15,20)=5) ในขณะที่  lcm(15,20)=5 X 3 X 4 พิจารณา

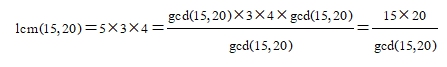
จากข้อสังเกตจึงสร้างเป็นทฤษฎีได้ดังนี้

ทฤษฎีบทที่ 2 กำหนดให้ และ เป็นจำนวนนับใด ๆ แล้ว

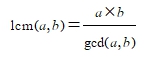
ตัวอย่างโจทย์ปัญหาค.ร.น.

ปัญหาข้อที่ 1 จงหาค.ร.น.ของ 5 15 18 20 45 60

วิธีทำ จากทฤษฎีบทที่ 1

           Lcm(5,15,18,20.45.60)=lcm(lcm(5,15,45),18,lcm(20,60))

                                               =lcm(45,18,60)

                                               =lcm(lcm(45,18),60)

จากทฤษฎีบทที่ 2

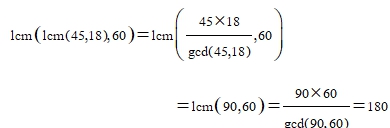
ปัญหาข้อที่ 2 จำนวนจำนวนหนึ่งเมื่อหารด้วย 10 15 และ 20 แล้วเหลือเศษ 9 จำนวนที่น้อยที่สุดที่สอดคล้องกับปัญหาดังกล่าวคือจำนวนใด

        เราสมมติให้จำนวนนั้นคือ n เราพบว่า ถ้า n ถูกหารด้วยด้วย 10 15 และ 20 จะเหลือเศษ 9 นั้นหมายความว่าหากเรานำเศษจากการหารออกจากตัวตั้งจะทำให้หารได้ลงตัวนั้นคือ 10 15 และ 20 สามารถหาร n-9 จากนิยามจะเห็นได้ว่า n-9 คือตัวคูณของ 10 15 และ 20 ดังนั้น n-9=lcm(10,15,20)=60

        ดังนั้น จำนวนนับ n=69 คือจำนวนนับที่น้อยที่สุดที่ถูกหารด้วย 10 15 และ 20 แล้วเหลือเศษ 9

ปัญหาข้อที่ 3 จำนวนจำนวนหนึ่งเมื่อหารด้วย 6 เหลือเศษ 4 หารด้วย 9 เหลือเศษ 7 และ หารด้วย 12 แล้วเหลือเศษ 10 จำนวนที่น้อยที่สุดที่สอดคล้องกับปัญหาดังกล่าวคือจำนวนใด

        เราสมมติให้จำนวนนั้นคือ n เราพบว่าหากเพิ่มอีก 2 จะทำให้ 6 9 และ 12 หารได้ลงตัวนั้นคือ n+2 = ค.ร.น.(6,9,12) = 36 จำนวนนั้นคือ 34

สรุป

            หากเราต้องเพิ่มปริมาณซ้ำ ๆของสิ่งของที่แตกต่างกันจนมีปริมาณที่เท่ากัน โดยปริมาณน้อยสุดที่ทำให้สิ่งของทั้งสองมีค่าเท่ากันเรียกว่า ตัวคูณร่วมน้อย นิยามของตัวคูณร่วมน้อยของจำนวนสองจำนวนในเชิงคณิตศาสตร์จึงหมายถึงจำนวนที่มีคุณสมบัติ 2 ข้อคือ 1) เป็นตัวคูณร่วมของจำนวนทั้งสอง และ 2) เป็นตัวคูณร่วมที่มีค่าน้อยที่สุด จากหลักการบวกลบเศษส่วนทำให้เราเห็นถึงข้อสังเกตที่นำไปสู่ทฤษฎีบทที่ 1 หากจำนวนน้อยสามารถหารจำนวนมากได้ลงตัวแล้ว ค.ร.น. ของจำนวนทั้งสองคือจำนวนมาก นอกจากนี้ข้อสังเกตจากการหา ค.ร.น. โดยวิธีตั้งหารยังแสดงถึงความสัมพันธ์ของ ห.ร.ม. และ ค.ร.น. กล่าวคือ ผลคูณของจำนวนสองจำนวนจะมีค่าเท่ากับผลคูณของ ห.ร.ม. และ ค.ร.น. ของจำนวนทั้งสองดังทฤษฎีบทที่ 2 ในส่วนสุดท้ายผู้เขียนได้ยกตัวอย่างโจทย์ปัญหาที่ประยุกต์ใช้ค.ร.น.เพื่อหาค่าจำนวนที่น้อยที่สุดที่สอดคล้องกับคุณสมบัติบางประการเพื่อเป็นแนวทางสาธิตการวิเคราะห์ และนำไปประยุกต์ใช้แก้ปัญหาอื่น ๆ

แหล่งที่มา

Paquin D. (2010). Stanford University educational program for gifted youth (EPGY) number theory summer 2010, 24-29.

Susanna S. E. (2011). Discrete Mathematics with applications 4th edition 2011 Brooks/Cole Cengage Learning Canada.