ตรรกศาสตร์
ตรรกศาสตร์
เป็นที่ทราบกันดีว่ากระบวนการทางวิทยาศาสตร์มีรูปแบบการค้นหาความรู้ที่เป็นเหตุเป็นผล ในทางกฏหมายก็ใช้การอ้างเหตุผลการตัดสิน พิพากษา ในเศรษฐศาสตร์และสังคมต่างก็โน้มน้าวและสร้างความน่าเชื่อถือด้วยกระบวนการที่เป็นเหตุเป็นผล จะเห็นว่าตรรกศาสตร์ซึ่งเป็นศาสตร์ที่ศึกษาเกี่ยวกับการใช้เหตุผลมีบทบาทสำคัญในการสร้างและพัฒนารากฐานให้กับศาสตร์ต่าง ๆ โดยเฉพาะอย่างยิ่งในคณิตศาสตร์ที่อาศัยเพียงโครงสร้างคณิตศาสตร์ ตรรกศาสตร์และการพิสูจน์ ก็สามารถค้นพบความจริงพร้อมตรวจสอบความจริงได้โดยไม่ต้องอาศัยเครื่องมืออื่น ที่สำคัญยิ่งคือศาสตร์ด้านคอมพิวเตอร์จำเป็นอาศัยตรรกศาสตร์ในการสั่งการทำงานของเครื่องจักร จะเห็นว่าตรรกศาสตร์ถูกนำไปหลากหลายบริบทตามศาสตร์นั้นด้วยเหตุนี้จึงมีความจำเป็นที่ต้องศึกษาตรรกศาสตร์เชิงสัญลักษณ์เพื่อสามารถนำไปประยุกต์ใช้ได้ในทุกบริบทดังที่กล่าวมาข้างต้น

ภาพที่ 1 ตารางดำเนินการทางตรรกศาสตร์
ที่มา วีระ ยุคุณธร
เป็นที่ทราบกันดีว่ากระบวนการทางวิทยาศาสตร์มีรูปแบบการค้นหาความรู้ที่เป็นเหตุเป็นผล ในทางกฏหมายก็ใช้การอ้างเหตุผลการตัดสิน พิพากษา ในเศรษฐศาสตร์และสังคมต่างก็โน้มน้าวและสร้างความน่าเชื่อถือด้วยกระบวนการที่เป็นเหตุเป็นผล จะเห็นว่าตรรกศาสตร์ซึ่งเป็นศาสตร์ที่ศึกษาเกี่ยวกับการใช้เหตุผลมีบทบาทสำคัญในการสร้างและพัฒนารากฐานให้กับศาสตร์ต่าง ๆ โดยเฉพาะอย่างยิ่งในคณิตศาสตร์ที่อาศัยเพียงโครงสร้างคณิตศาสตร์ ตรรกศาสตร์และการพิสูจน์ ก็สามารถค้นพบความจริงพร้อมตรวจสอบความจริงได้โดยไม่ต้องอาศัยเครื่องมืออื่น ที่สำคัญยิ่งคือศาสตร์ด้านคอมพิวเตอร์จำเป็นอาศัยตรรกศาสตร์ในการสั่งการทำงานของเครื่องจักร จะเห็นว่าตรรกศาสตร์ถูกนำไปหลากหลายบริบทตามศาสตร์นั้นด้วยเหตุนี้จึงมีความจำเป็นที่ต้องศึกษาตรรกศาสตร์เชิงสัญลักษณ์เพื่อสามารถนำไปประยุกต์ใช้ได้ในทุกบริบทดังที่กล่าวมาข้างต้น
ประพจน์
ในระบบการอ้างเหตุผลจะมีข้อความซึ่งเป็นกุญแจสำคัญถูกใช้ในการสรุปเรียกว่าสมมติฐาน ข้อความเหล่านี้ต้องได้รับการยอมรับและมีค่าความจริงเป็นจริงจึงนำมาสู่ผลที่เกิดขึ้น แต่หากข้อความที่เป็นสมมติฐานเป็นเท็จจะไม่สามารถสรุปผลได้ตัวอย่างเช่นเราตั้งข้อความที่เป็นสมมติฐานไว้ว่า “เกิดฝนตก” ผลที่เกิดขึ้นคือ ”ถนนเส้นนี้จะต้องเปียก” จะเห็นว่าข้อความที่เป็นสมมติฐานนั้นสามารถบอกได้ว่าจริงหรือเท็จ ถ้าฝนตกจริงเราก็สามารถสรุปได้ว่าถนนจะต้องเปียกอย่างแน่นอน แต่ถ้าฝนไม่ได้ตก(ฝนตกเป็นเท็จ) เราจะไม่สามารถสรุปได้ว่าถนนเปียกหรือไม่ ข้อความสมมติฐานจำเป็นจะต้องเป็นข้อความที่สามารถบอกได้ว่าจริงหรือเท็จอย่างใดอย่างหนึ่ง เราเรียกข้อความประเภทนี้ว่า ประพจน์ ตัวอย่างข้อความที่เป็นประพจน์เช่น “78 > 60” “พลเอกประยุทธ์ จันทร์โอชาเป็นนายกรัฐมนตรีของประเทศไทย” และ ”ประเทศไทยมี 77 จังหวัด” สำหรับตัวอย่างของข้อความที่เป็นเท็จได้แก่ “78 < 60” “กาญจนบุรีเป็นจังหวัดที่อยู่ในภาคกลางของประเทศไทย” และ “0 ไม่ใช่จำนวนคู่” เป็นต้น
หากเราพิจารณาข้อความข้างต้นจะเห็นว่า ข้อความดังกล่าวสามารถบอกได้ว่าเป็นจริงหรือเป็นเท็จ โดยไม่เกี่ยวข้อกับความรู้สึกหรือความเชื่อ แต่หากมีการใช้ความรู้สึกหรือความเชื่อในการตัดสินเช่นข้อความที่กล่าวว่า กาแฟร้านที่ 1 หอมกว่ากาแฟร้านที่ 2 แม้ว่าข้อความเหล่านี้อาจจะเป็นจริงหรือเป็นเท็จอย่างใดอย่างหนึ่งภายใต้ความรู้สึกหรือความคิดของแต่ละบุคคล แต่เราจะไม่ถือว่าข้อความนี้เป็นประพจน์ตามหลักตรรกศาสตร์ เพราะหากเรานำข้อความกลุ่มนี้ไปตั้งเป็นสมมติฐานแล้วจะนำมาซึ่งข้อสรุปที่ไม่เป็นเอกภาพ จะเห็นได้ว่าข้อความที่เป็นสมมติฐานนั้นต้องเป็นประพจน์ซึ่งมีบทบาทสำคัญต่อกลไกการอ้างเหตุผลเชิงตรรกศาสตร์เพราะค่าความสมมติฐานที่เปลี่ยนไปจะนำมาซึ่งข้อสรุปที่ต่างกันด้วย
อย่างไรก็ตามในกระบวนการอ้างเหตุผลนั้นจะมีข้อความอย่างน้อย 2 ข้อความคือข้อความที่เป็นสมมติฐาน และข้อความที่เป็นข้อสรุป แต่ในบ้างครั้งการจะตัดสิน หรือสรุปผลของเหตุการณ์ต่าง ๆ อาจมีสมมติฐานมากกว่าหนึ่งข้อ หรืออาจได้ข้อสรุปมากว่าหนึ่งข้อก็เป็นได้ ในหัวข้อถัดไปจึงเป็นการศึกษาการเชื่อมโยงระหว่างข้อความตั้งแต่สองข้อความขึ้นไป
การดำเนินการเชิงตรรกศาสตร์
การเชื่อมโยงระหว่างประพจน์ตั้งแต่สองประพจน์ขึ้นไปแล้วทำให้เกิดประพจน์ใหม่ เราเรียกการเชื่อมโยงนี้ว่าการดำเนินการเชิงตรรกศาสตร์ ตัวดำเนินการเชิงตรรกศาสตร์ประกอบด้วยคำว่า “และ” “หรือ” “ถ้า-แล้ว” และ“ก็ต่อเมื่อ” นอกจากนี้ยังมีตัวดำเนินการนิเสธซึ่งไม่ได้ทำหน้าที่เชื่อมประพจน์ตั้งแต่สองประพจน์ขึ้นไป แต่ใช้สร้างประพจน์ที่มีความจริงตรงกันช้ามกับประพจน์หนึ่ง
ตัวดำเนินการนิเสธ
ดังที่กล่าวมาในข้างต้นการดำเนินการนิเสธจะทำให้ได้ประพจน์ที่มีค่าความจริงตรงกันข้ามกับประพจน์เดิมด้วยการเพิ่มคำว่า “ไม่” ลงในประพจน์ตั้งต้นนั้นคือถ้าเรากำหนดให้ P เป็นประพจน์แล้วนิเสธของ P เขียนแทนด้วย “P’” จะได้ว่า
กรณีที่ 1 ประพจน์ P มีค่าความจริง ( T ) จะได้ว่า P’ เป็นประพจน์ที่มีค่าความจริงเป็นเท็จ ( F )
กรณีที่ 2 ประพจน์ P มีค่าความเท็จ ( F ) จะได้ว่า P’ เป็นประพจน์ที่มีค่าความจริงเป็นจริง ( T )
ตัวอย่างเช่น ให้ P := 78 > 60 มีค่าความจริงเป็นจริงดังนั้น P’ := “78 ไม่มาก 60”หรือ “78 น้อยกว่าหรือเท่ากับ 60” มีค่าความจริงเป็นเท็จ ในทำนองเดียวกันถ้าให้ P := 78 < 60 ซึ่งมีค่าความจริงเป็นเท็จแล้วประพจน์ P’ := “78 ไม่น้อยกว่า 60” หรือ “78 มากกว่าหรือเท่ากับ 60” จะค่าความจริงเป็นจริง
การเชื่อมประพจน์ด้วยตัวดำเนินการหรือ
ในตัวอย่างข้างต้นเราจะพบการใช้คำว่าหรือเชื่อมระหว่างประพจน์สองประพจน์คือข้อความ “78 มากกว่าหรือเท่ากับ 60” ซึ่งมีค่าความจริงเป็นจริง ประกอบด้วยประพจน์ย่อย 2 ประพจน์คือ “78 มากกว่า 60” กับ “78 เท่ากับ 60” เชื่อมกันด้วยคำว่าหรือ มีค่าความจริงเป็นจริงและเป็นเท็จตามลำดับ สังเกตว่าเมื่อเชื่อมกันด้วยคำว่าหรือแล้วประพจน์ดังกล่าวความมีค่าความจริงเป็นจริง นั้นแสดงว่าประพจน์ที่มีใช้คำเชื่อมหรือหากมีประพจน์ย่อยอย่างน้อยหนึ่งประพจน์เป็นจริงแล้วประพจน์ดังกล่าวจะเป็นจริงด้วย กล่าวได้อีกว่าคำเชื่อมหรือนั้นเป็นคำเชื่อมเผื่อเลือก เมื่อกำหนดให้ P และ Q เป็นประพจน์ P หรือ Q จะเป็นเท็จ เมื่อ P เป็นเท็จ และ Q เป็นเท็จ
ข้อควรระวังการตีความคำว่าหรือ ในทางภาษานั้น หรือ อาจให้ความหมายอีกนัยยะคือ หรือ แบบให้เลือกอย่างใดอย่างหนึ่งเช่นจำนวนเต็มใด ๆเป็นจำนวนคี่ หรือ จำนวนคู่ ซึ่งจะเห็นว่าประพจน์ย่อยจะเป็นจริงทั้งคู่ไม่ได้ แต่ในทางตรรกศาสตร์ถ้า P เป็นจริงและ Q เป็นจริง P หรือ Q เป็นจริง
การเชื่อมประพจน์ด้วยตัวดำเนินการ
สมมติให้ P := “10 < 25” และ Q := “10 > 5” จะเห็นว่าต่างมีค่าความจริงเป็นจริงทั้งคู่ พิจารณาข้อความ P และ Q := “10 < 25 และ 10 > 5” อาจเขียนได้เป็น “5 < 10 <25 “ ซึ่งเป็นจริง แต่หากมีประพจน์ย่อยประพจน์หนึ่งเป็นเท็จจะทำให้ประพจน์ที่เชื่อมด้วยคำว่าและเป็นเท็จทันที นั้นคือประพจน์ P และ Q จะเป็นจริง เมื่อ P เป็นจริง และ Q เป็นจริง
การเชื่อมประพจน์ด้วยตัวดำเนินการถ้าแล้ว
รูปแบบการเชื่อมที่สาม เป็นการเชื่อมประพจน์ 2 ประพจน์ในรูปของการแจงเหตุสู่ผลโดยจะมีประพจน์หนึ่งเป็นเหตุสมมติให้แทนด้วย P และอีกประพจน์หนึ่งเป็นผลแทนด้วย Q ข้อความแจงเหตุสู่ผลจะเขียนในรูปของ “ถ้า P แล้ว Q” เราจะยกตัวอย่างด้วยข้อความที่เป็นที่ทราบกันดีว่าถ้าเรานำสองไปหารจำนวนนับใด ๆได้ลงตัวจำนวนนั้นจะเป็นจำนวนคู่ เราจะพิจารณาค่าความจริงกรณีที่ P และ Q ถูกเชื่อมด้วย “ถ้า-แล้ว”ดังนี้
กรณีที่ 1 กรณีที่ประพจน์ของเหตุและผลเป็นจริงทั้งคู่
กำหนดให้ P := 10 หารด้วย 2 ลงตัว และ Q := 10 เป็นจำนวนคู่ จะเห็นว่า ถ้า 10 หาร 2 ลงตัวแล้ว 10 เป็นจำนวนคู่เป็นจริง
กรณีที่ 2 กรณีที่ประพจน์ของเหตุเป็นจริงแต่ประพจน์ของผลเป็นเท็จ
กำหนดให้ P := 10 หารด้วย 2 ลงตัว และ Q := 10 ไม่เป็นจำนวนคู่ จะเห็นว่า ถ้า 10 หาร 2 ลงตัวแล้ว 10 เป็นไม่จำนวนคู่เป็นเท็จ
สำหรับอีก 2 กรณีที่เหลือมักจะความสับสนให้กับผู้ที่ศึกษาตรรกศาสตร์คือกรณีที่ประพจน์ของเหตุเป็นเท็จ
กรณีที่ 3 กำหนดให้ P := 10 หารด้วย 2 ไม่ลงตัว และ Q := 10 เป็นจำนวนคู่ พิจารณา ถ้า 10 หาร 2 ลงตัวไม่ลงตัว แล้ว 10 เป็นจำนวนคู่ จะเห็นว่าไม่ว่า 10 จะหารสองลงตัวหรือไม่ก็ตาม 10 ยังคงเป็นจำนวนคู่อย่างแน่นอนนั้นคือหากค่าความจริงของประพจน์ที่เป็นผลเป็นจริงแล้วประพจน์ที่เชื่อมด้วย “ถ้า-แล้ว” เป็นจริงเสมอ
กรณีที่ 4 กำหนดให้ P := 10 หารด้วย 2 ไม่ลงตัว และ Q := 10 ไม่เป็นจำนวนคู่ พิจารณา ถ้า 10 หาร 2 ลงตัวไม่ลงตัว แล้ว 10 ไม่เป็นจำนวนคู่ข้อนี้เป็นจริง เนื่องจากประพจน์เหตุที่เป็นเท็จย่อมนำมาซึ่งการผลที่เป็นเท็จ ดังนั้นการที่เชื่อมด้วย “ถ้า-แล้ว” เมื่อประพจน์ของเหตุและผลเป็นเท็จทั้งคู่ย่อมเป็นประพจน์ที่มีค่าความจริงเป็นจริงเสมอ
จากทั้งสี่กรณีประพจน์ที่มีคำเชื่อม “ถ้า-แล้ว” จะเป็นเท็จเมื่อ ประพจน์ของเหตุเป็นจริงแต่ประพจน์ของผลเป็นเท็จ
การเชื่อมประพจน์ด้วยตัวดำเนินการก็ต่อเมื่อ
คำเชื่อม “ก็ต่อเมื่อ” เป็นคำที่ใช้แสดงความเป็นเหตุเป็นผลซึ่งกันและกันของประพจน์สองประพจน์นั้นคือ P ก็ต่อเมื่อ Q หมายถึง ( ถ้า P แล้ว Q ) และ ( ถ้า Q แล้ว P ) จะเห็นว่าข้อความก็ต่อเมื่อประกอบด้วยประพจน์ย่อย 2 ประพจน์เชื่อมด้วยคำว่าและดังนั้น
กรณีที่ P ก็ต่อเมื่อ Q เป็นจริงเกิดจาก “ถ้า P แล้ว Q “ เป็นจริง และ “ถ้า Q แล้ว P“ เป็นจริงนั้นคือทั้ง P และ Q จะต้องเป็นจริง หรือ เป็นเท็จพร้อมกัน
กรณีที่ P ก็ต่อเมื่อ Q เป็นเท็จเกิดจาก “ถ้า P แล้ว Q “ เป็นเท็จ หรือ “ถ้า Q แล้ว P“ เป็นเท็จนั้นคือทั้ง P และ Q จะต้องเป็นจริง หรือ เป็นเท็จไม่พร้อมกัน
จะเห็นว่าถ้า P และ Q มีค่าความจริงเหมือนกันแล้ว P ก็ต่อเมื่อ Q จะเป็นจริง แต่ถ้า P และ Q มีค่าความจริงต่างกัน P ก็ต่อเมื่อ Q เป็นเท็จ
กลับไปที่เนื้อหา

ภาพที่ 2 สัญลักษณ์ตัวบ่งปริมาณ
ที่มา วีระ ยุคุณธร
ประโยคทางตรรกศาสตร์ทั่วไปจะประกอบไปด้วย ประธาน + กริยา (เป็น/ไม่เป็น) + ภาคแสดงคุณลักษณะหรือความสัมพันธ์บางอย่างเช่น n เป็นจำนวนเต็มที่ยกกำลัง 2 แล้วเท่ากับ 1 จะเห็นค่าความจริงของข้อความนี้ขึ้นกับ n กำหนดให้ P(n) := n เป็นจำนวนเต็มที่ยกกำลัง 2 แล้วเท่ากับ 1 พิจารณา P(1) = 12 = 1 และ P(-1) = (-1)2 = 1 แต่ P(2) = 22 = 4 จะเห็นว่าเมื่อ n = 1 และ -1 ข้อความ P(n) เป็นจริง แต่เมื่อ n =-2 ข้อความ P(n) เป็นเท็จ เราเรียก P(n) ว่าประโยคเปิดซึ่งค่าความจริงของประโยคเปิดจะขึ้นกับตัวแปร แต่ถ้าเราพิจารณาประธานประโยคในเชิงปริมาณโดยพิจารณาเพียงบางส่วน (For some) หรือ มี (There exists) และพิจารณาทั้งหมด (For all) ประโยคเปิดข้างต้นจะกลายเป็นประพจน์ดังต่อไปนี้
Exists: มีจำนวนเต็มที่ยกกำลัง 2 แล้วเท่ากับ 1 จะเห็นว่าข้อความนี้เป็นจริงเพราะมี 1 และ -1
All: จำนวนเต็มทุกจำนวนยกกำลัง 2 แล้วเท่ากับ 1 จะเห็นว่าข้อความนี้เป็นเท็จเพราะ 22 = 4
การใช้ตัวบ่งปริมาณกรณีที่มีประธาน 2 สิ่งแบ่งเป็น 4 กรณีได้แก่
- All x All y บ่งบอกถึงการพิจารณา x และ y ใด ๆ กล่าวถึงปริมาณทั้งหมดของประธานทั้งสองกลุ่ม
- Exists x Exists y บ่งบอกถึงการมี x และ y กล่าวถึงปริมาณบางส่วนของประธานทั้งสองกลุ่ม
- Exists x All y บ่งบอกถึงการมี x สำหรับทุก y กล่าวถึงมีสมาชิกในกลุ่มแรกสำหรับสมาชิกทั้งหมดของกลุ่มสอง
- All x Exists y บ่งบอกถึงทุกทุก x จะมี y กล่าวถึงสมาชิกแต่ละตัวของกลุ่มแรกจะมีสมาชิกในกลุ่มที่สอง
คำอธิบายในกรณีที่ 3 และ 4 นั้นอาจทำให้เกิดความสับสนผู้เขียนจึงอธิบายดังรูป โดยการมีในที่นี้อาจมีปริมาณมากกว่า 1 ก็ได้
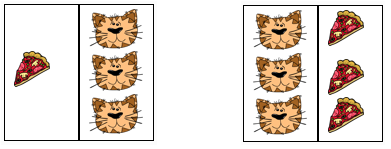
มีพิซซ่าสำหรับแมวทุกตัว แมวทุกตัวมีพิซซ่า
ภาพที่ 3 ความแตกต่างของลำดับ All และ exists
ที่มา วีระ ยุคุณธร ที่มา http://www.clker.com/
ดัดแปลงจาก Skvarcius R. and Robinson W.B., หน้า 34
การวิเคราะห์ค่าความจริงของตัวบ่งปริมาณ 1 ตัวแปร
All x, P(x) เป็นจริง เมื่อทุกค่า x ทำให้ P(x) เป็นจริง
All x, P(x) เป็นเท็จ หรือ นิเสธของ All x, P(x) นั้นคือไม่ใช่ทุก x ที่ทำให้ P(x) เป็นจริง แสดงว่ามี x ที่ทำให้ P(x) เป็นเท็จดังนั้น All x, P(x) เป็นเท็จ เมื่อมี x ที่ทำให้ P(x) เป็นเท็จ
Exists x, P(x) เป็นจริง เมื่อมี x ที่ทำให้ P(x) เป็นจริง
Exists x, P(x) เป็นเท็จ หรือ นิเสธของ Exists x, P(x) นั้นคือไม่มี x ที่ทำให้ P(x) เป็นจริง แสดงว่าทุกค่า x ทำให้ P(x) เป็นเท็จดังนั้น Exists x, P(x) เป็นเท็จ เมื่อทุก x ที่ทำให้ P(x) เป็นเท็จ
ตัวอย่าง กำหนดให้ k เป็นจำนวนเต็มพิจารณา
“All k, k2 มากกว่าหรือเท่ากับ 0” ประพจน์เป็นจริง เพราะว่า ผลคูณของจำนวนเต็มบวกเป็นจำนวนเต็ม ผลคูณของจำนวนเต็มลบเป็นจำนวนเต็มบวก และผลคูณของศูนย์กับศูนย์มีค่าเท่ากับ 0
“All k, k2 มากกว่า 0” ประพจน์เป็นเท็จ เพราะว่ามีศูนย์ที่เป็นจำนวนเต็มซึ่ง 02 ไม่มากกว่า 0
“Exists k, k2 เท่ากับ 0” ประพจน์เป็นจริง เพราะว่ามีศูนย์ที่เป็นจำนวนเต็มซึ่ง 02 เท่ากับ 0
“Exists k, k2 น้อยกว่า 0” ประพจน์เป็นเท็จ เพราะว่าจำนวนเต็มใด ๆยกกำลัง 2 จะมากกว่าศูนย์หรือเท่ากับศูนย์
การวิเคราะห์ค่าความจริงของตัวบ่งปริมาณ 2 ตัวแปร
All x All y, P(x,y) เป็นจริง เมื่อทุกค่า x และ y ทำให้ P(x,y) เป็นจริง
All x All y, P(x,y) เป็นเท็จ หรือ นิเสธของ All x All y, P(x,y) นั้นคือมี x หรือ y บางตัวที่ทำให้ P(x,y) เป็นเท็จ
Exists x Exists y, P(x,y) เป็นจริง เมื่อมีค่า x และ y ที่ทำให้ P(x,y) เป็นจริง
Exists x Exists y, P(x,y) เป็นเท็จ เมื่อทุกค่า x และ y ทำให้ P(x,y) เป็นเท็จ
Exists x All y, P(x,y) เป็นจริง เมื่อมีค่า x สำหรับทุกค่า y ที่ทำให้ P(x,y) เป็นจริง
Exists x All y, P(x,y) เป็นเท็จ เมื่อทุกค่า x มี y ที่ทำให้ P(x,y) เป็นเท็จ
All x Exists y, P(x,y) เป็นจริง เมื่อทุกค่า x มี y ที่ทำให้ P(x,y) เป็นจริง
All x Exists y, P(x,y) เป็นเท็จ เมื่อมีค่า x สำหรับทุกค่า y ที่ทำให้ P(x,y) เป็นเท็จ
ตัวอย่างเช่น กำหนดให้ x เป็นจำนวนเต็มคู่ และ y เป็นจำนวนเต็มคี่
All x All y, x+y เป็นจำนวนเต็มคี่ ประพจน์เป็นจริง เนื่องจากจำนวนเต็มคู่สามารถเขียนได้ในรูป 2m และจำนวนเต็มคี่สามารถเขียนได้ในรูป 2n+1 เมื่อ m,n เป็นจำนวนเต็ม จะเห็นว่าผลบวก 2m+2n+1 = 2(m+n)+1 เป็นจำนวนเต็มคี่
All x All y, xy ไม่เป็นจำนวนเฉพาะ ประพจน์เป็นเท็จ เนื่องจากมี x = 2 และ y = 1 จะได้ว่า xy = 2 เป็นจำนวนเฉพาะ
Exists x Exists y, xy เป็นจำนวนเฉพาะ ประพจน์เป็นจริง เนื่องจากมี x = 2 และ y =1 ซึ่ง xy = 2 เป็นจำนวนเฉพาะ
Exists x Exists y, x+y เป็นจำนวนคู่ ประพจน์เป็นเท็จ เนื่องจากผลคูณของจำนวนคู่และจำนวนคี่ใด ๆเป็นจำนวนคี่เสมอ
Exists x All y, xy ไม่เป็นจำนวนเฉพาะ ประพจน์เป็นจริง เนื่องจากมี x = 0 ที่ทำให้จำนวนเต็มคี่ y ใด ๆเมื่อคูณด้วยศูนย์จะเท่ากับศูนย์ซึ่งไม่เป็นจำนวนเฉพาะ (0y = 0)
Exists x All y, xy เป็นจำนวนเฉพาะ ประพจน์เป็นเท็จ เนื่องจากไม่ว่า x จะเป็นจำนวนคู่ใด ๆ จะมี y ที่มากกว่า 1 ซึ่ง xy > 2 ซึ่งไม่เป็นจำนวนเฉพาะ
All x Exists y, xy เป็นไม่จำนวนเฉพาะ ประพจน์เป็นจริง เนื่องจากไม่ว่า x จะเป็นจำนวนคู่ใด ๆ จะมี y ที่มากกว่า 1 ซึ่ง xy > 2 ซึ่งไม่เป็นจำนวนเฉพาะ
All x Exists y, xy เป็นจำนวนเฉพาะ ประพจน์เป็นเท็จ เนื่องจากมี x = 0 ที่ทำให้จำนวนเต็มคี่ y ใด ๆเมื่อคูณด้วยศูนย์จะเท่ากับศูนย์ซึ่งไม่เป็นจำนวนเฉพาะ (0y = 0)
จากตัวอย่างข้างต้นให้สังเกตการให้เหตุผลจะพบว่า
- นิเสธของ All x All y, x+y เป็นจำนวนเต็มคี่ คือ Exists x Exists y, x+y เป็นจำนวนคู่
- All x All y, xy ไม่เป็นจำนวนเฉพาะ เป็นนิเสธของ Exists x Exists y, xy เป็นจำนวนเฉพาะ
- นิเสธของ Exists x All y, xy ไม่เป็นจำนวนเฉพาะ คือ All x Exists y, xy เป็นจำนวนเฉพาะ
- Exists x All y, xy เป็นจำนวนเฉพาะ เป็นนิเสธของ All x Exists y, xy เป็นไม่จำนวนเฉพาะ
โดยเฉพาะข้อสังเกตที่ 3 กับข้อสังเกตที่ 4 นั้นผู้อ่านจะต้องนึกไว้เสมอว่านิเสธของประพจน์จะต้องมาจากการพิจารณาการให้เหตุผลแม้ว่า Exists x All y, xy ไม่เป็นจำนวนเฉพาะ จะเป็นจริง และ Exists x All y, xy เป็นจำนวนเฉพาะ จะเป็นเท็จ ซึ่งให้ค่าความจริงตรงกันข้ามกันเป็นเพียงการสมมูลกันทางตรรกศาสตร์ logical equivalent แต่ไม่ได้หมายความว่าข้อความสมข้อความนี้เป็นเสธกัน
กลับไปที่เนื้อหา

ภาพที่ 4 ปกบทเรียนเรื่องตรรกศาสตร์กับคอมพิวเตอร์
ที่มา วีระ ยุคุณธร ดัดแปลงจาก https://upload.wikimedia.org/wikipedia/commons/8/82/CharlesBabbage.jpg, https://upload.wikimedia.org/wikipedia/commons/a/a1/Alan_Turing_Aged_16.jpg
คอมพิวเตอร์ถูกนำมาใช้เพื่ออำนวยความสะดวก และแก้ปัญหาต่าง ๆ ได้อย่างมีประสิทธิภาพ ผ่านการสั่งงานในรูปของอัลกอริทึม ซึ่งมีการอธิบายการทำงานแตกต่างกันไปตามชนิดของเครื่องมือที่เลือกใช้อาทิ
- ภาษาธรรมชาติ หรือภาษาที่ใช้ในชีวิตประจำวัน(ภาษาอังกฤษ) ทำให้เข้าถึงได้รวดเร็วไม่จำเป็นต้องศึกษาภาษาอื่นเพิ่มเติมแต่อาจมีอุปสรรคเพราะการสั่งงานด้วยภาษาธรรมชาติมักเกิดความคลุมเครือทำให้ไม่ได้ผลลัพธ์ในแบบที่ต้องการ ในขณะที่อัลกอริทึมนั้นไม่ต้องการให้มีความคลุมเครือในการทำงาน
- ภาษาเครื่องจักร หรือ ภาษาโปรแกรมคอมพิวเตอร์ที่มีการทำงานแบบเป็นเหตุเป็นผลที่แน่นอน ปลาสจากความสำนึกรู้ นั้นทำให้รายละเอียดเล็กๆ น้อยๆต้องถูกตัดทิ้งไปในการใช้ภาษาคอมพิวเตอร์
- การเขียนแผนผังเป็นเครื่องมือที่ช่วยให้เราเข้าใครโครงสร้างของอัลกอริทึมได้ชัดเจน แต่ข้อเสียคือถ้าขั้นตอนการทำงานนั้นมีความซับซ้อนมีความเป็นอิสระในการควบคุม เงื่อนไขที่ซับซ้อน และวงวนเหล่านี้อาจทำให้การเขียนแผนผังเป็นไปได้ยาก และมีความซับซ้อนเกินกว่าจะเข้าใจได้ง่าย
- ซูโดโคด เป็นโครงสร้างภาษาที่คล้ายกับภาษาคอมพิวเตอร์ และภาษาธรรมชาติทำให้ง่ายต่อการเปลี่ยนซูโดโคดไปเป็นภาษาธรรมชาติร่วมไปถึงการแปลงไปเป็นภาษาคอมพิวเตอร์อื่นอีกด้วย
ดังที่กล่าวมาข้างต้นจะเห็นว่าซูโดโคดนั้นใช้รูปแบบภาษาที่ผสมผสานระหว่างภาษาธรรมชาติและภาษาคอมพิวเตอร์ที่ยังคงรักษาความแจ่มชัดในการทำงานทำให้สอดคล้องการภาษาทางตรรกศาสตร์ที่มีความรัดกุมแจ่มชัดทำให้การสั่งงานคอมพิวเตอร์อยู่ในรูปของประโยคแบบมีเงื่อนไง (If-Then)
ประโยคแบบมีเงื่อนไข
ในทางตรรกศาสตร์ข้อความ”ถ้า-แล้ว” เป็นข้อความที่ใช้แสดงความเป็นเหตุเป็นผลเช่นข้อความ ถ้า P แล้ว Q เราจะเรียก P ว่าสมมติฐานและเรียก Q ว่าข้อสรุปหลักการนี้จึงถูกนำมาใช้ในการสั่งงานคอมพิวเตอร์โดยที่ P คือเงื่อนไข และ Q คือคำสั่งเปรียบเทียบภาษาทั้ง 4 แบบจะได้ว่า
ภาษาธรรมชาติ ถ้าเงื่อนไข P เป็นจริงให้ทำตามคำสั่ง Q
ภาษาโปรแกรม excel =If(P,Q)
แผนผัง
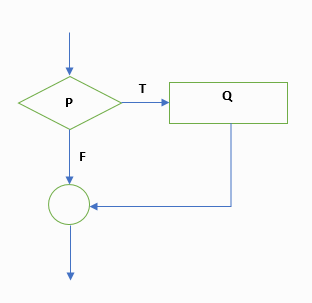
ภาพที่ 5 แผนผังอัลกอริทึม If-then
ที่มา วีระ ยุคุณธร ดัดแปลงจาก
Skvarcius R. and Robinson W.B., หน้า 12
Psudocode If P then Q
แต่ในทางคอมพิวเตอร์นั้นถ้าจากตรวจสอบแล้วพบว่าไม่เป็นไปตามเงื่อนไขเราสามารถสั่งคำสั่งทางเลือกได้โดยใช้รูปแบบคำสั่ง If-then-else
ภาษาธรรมชาติ ถ้าเงื่อนไข P เป็นจริงให้ทำตามคำสั่ง Q1 แต่ถ้าเงื่อนไข P เป็นเท็จให้ทำตามคำสั่ง Q2
ภาษาโปรแกรม excel =If (P,Q1,Q2)
แผนผัง
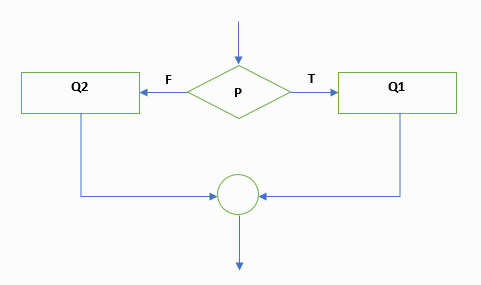
ภาพที่ 6 แผนผังอัลกอริทึม If-then-else
ที่มา วีระ ยุคุณธร ดัดแปลงจาก
Skvarcius R. and Robinson W.B., หน้า 12
Psudocode If P then Q1 else Q2
ตัวอย่างที่ 1 การหาค่าสัมบูรณ์ของจำนวนเต็ม
ภาษาธรรมชาติ จากนิยามค่าสัมบูรณ์ | x | จะพบว่าถ้า x เป็นจำนวนจริงที่ไม่เป็นลบแล้ว | x | = x แต่ถ้า x เป็นจำนวนจริงที่เป็นลบ | x | = -x
ภาษาโปรแกรม excel =If ( x<0 , |x| = -x , |x| = x)

ภาพที่ 7 ผลการทำงานตามอัลกอริทึมหาค่าสัมบูรณ์ด้วยโปรแกรม excel
ที่มา วีระ ยุคุณธร
แผนผัง
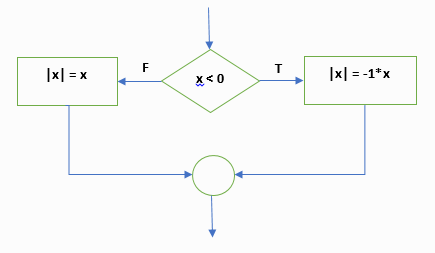
ภาพที่ 8 แผนผังอัลกอริทึมการหาค่าสัมบูรณ์
ที่มา วีระ ยุคุณธร
Psudocode If x<0 then |x|=-x else |x|=x
ตัวอย่างที่ 2 การวิเคราะห์ชนิดของค่ารากสมการกำลังสองด้วย discriminant
พิจารณาสมการกำลังสองในรูปของ ax2 + bx + c = 0
ax2 + bx + c = a [ x2 + (b/a)x + (c/a) ]
=a[ {x – (b/2a) }2 – (b/2a)2+(c/a) ]
=a[ {x – (b/2a) }2 – (b/2a)2+(c/a) ]
=a[ {x – (b/2a) }2 – { (b2-4ac) / (2a) } ]
แยกพิจารณาค่า b2-4ac เรียกว่า discriminantได้ดังนี้
ภาษาธรรมชาติ
กรณีที่ 1 ถ้า b2-4ac < 0 จะได้สมการไม่มีรากเป็นจำนวนจริง
กรณีที่ 2 ถ้า b2-4ac = 0 จะได้สมการมีรากซ้ำ
กรณีที่ 3 ถ้า b2-4ac > 0 จะได้ว่าสมการมีรากเป็นจำนวนจริงที่แตกต่างกัน
ภาษาโปรแกรม excel ==IF(F3^2-4*E3*G3<0,"สมการไม่มีรากเป็นจำนวนจริง",IF(F3^2-4*E3*G3=0,"สมการมีรากซ้ำ","สมการมีรากเป็นจำนวนจริงที่แตกต่างกัน"))
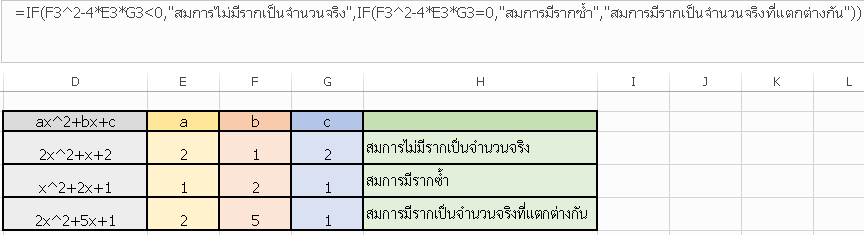
ภาพที่ 9 ผลการทำงานตามอัลกอริทึมวิเคราะห์ค่ารากสมการกำลังสองด้วยโปรแกรม excel
ที่มา วีระ ยุคุณธร
แผนผัง
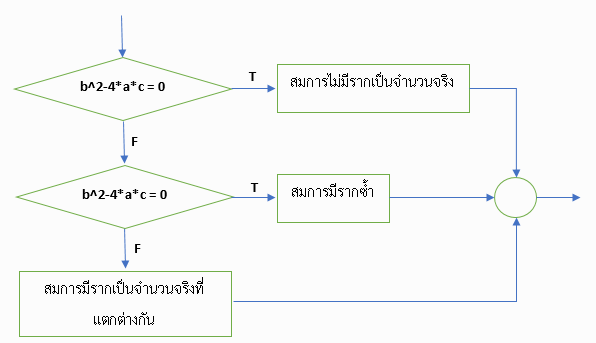
ภาพที่ 10 แผนผังอัลกอริทึมการวิเคราะห์ค่ารากสมการกำลังสอง
ที่มา วีระ ยุคุณธร
Psudocode If b2-4ac < 0 then แสดงข้อความ”สมการไม่มีรากเป็นจำนวนจริง”
else, If b2-4ac = 0 then แสดงข้อความ”สมการมีรากซ้ำ”
else แสดงข้อความ”สมการมีรากเป็นจำนวนจริงที่แตกต่างกัน”
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
กลับไปที่เนื้อหา



