การหาร ระดับชั้น ป.3
การหาร การหารลงตัว การหารไม่ลงตัว
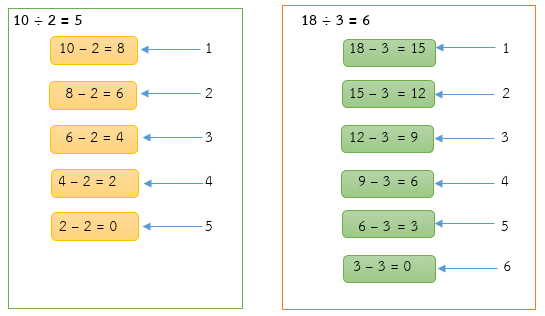
การหาร คือ การแบ่งออกหรือเอาออกครั้งละเท่า ๆ กัน หลายๆ ครั้ง จนได้ค่าเศษเป็น “0” เรียกว่า การหารลงตัว แต่ถ้าค่าเศษไม่เป็น “0” เรียกว่า การหารไม่ลงตัว

ภาพประกอบบทเรียนเรื่องการหาร
ที่มา : ปิยวดี เอ่งฉ้วน
- ประโยคสัญลักษณ์ 10 ÷ 2 = 5 อ่านว่า สิบหารด้วยสอง เท่ากับห้า
เรียก ÷ ว่า เครื่องหมายหาร
เรียก 10 ว่า ตัวตั้ง แทน A
เรียก 2 ว่า ตัวหาร แทน B
เรียก 5 ว่า ผลหาร แทน C
- ความสัมพันธ์ของการคูณ และการหาร โดยใช้ DIY MATH FAMILY TRIANGLES
A B = C
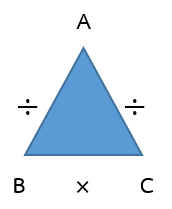
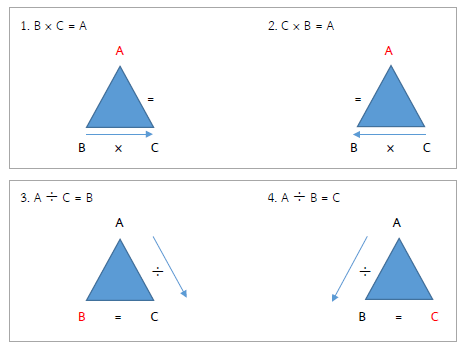
DIY MATH FAMILY TRIANGLES การคูณกับการหาร จะได้ ดังนี้
ตัวอย่างที่ 1 10 ÷ 2 = 5 .............................. (A B = C)
DIY MATH FAMILY TRIANGLES การคูณกับการหาร
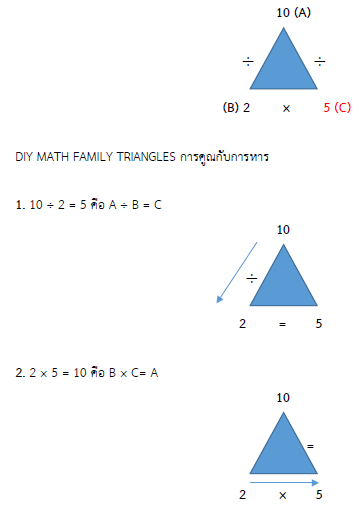
ดังนั้น การหาผลหารของ 10 ÷ 2 = 5
ตรวจคำตอบ
DIY MATH FAMILY TRIANGLES การคูณกับการหาร
B × C = A
2 × 5 = 10
แสดงว่า 10 ÷ 2 = 5 เป็นคำตอบที่ถูก
- การหารลงตัว
การหารลงตัว คือ การแบ่งจำนวนทีละจำนวนเท่า ๆ กัน โดยแบ่งแล้วพอดี มีเศษเป็น 0
ตัวอย่างที่ 2 18 ÷ 3 = 6
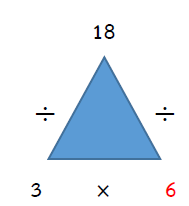
จากสามเหลี่ยมความสัมพันธ์ระหว่างการคูณกับการหาร จะได้ ดังนี้
18 ÷ 3 = 6 (1)
18 ÷ 6 = 3 (2)
3 × 6 = 18 (3)
6 × 3 = 18 (4)
ดังนั้น การหาผลหารของ 18 ÷ 3 = 6
ตรวจคำตอบ
DIY MATH FAMILY TRIANGLES การคูณกับการหาร
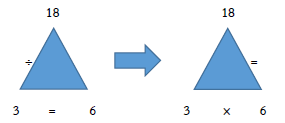
B × C = A
3 × 6 = 18
แสดงว่า 18 ÷ 3 = 6 เป็นคำตอบที่ถูก
- การหารไม่ลงตัว
การหารโดยลบตัวตั้งด้วยตัวหารซ้ำ ๆ กัน จนกระทั้งได้ผลลบน้อยกว่าตัวหาร และมากกว่าศูนย์ เป็นการหารไม่ลงตัว หรือการหารเหลือเศษ ผลลบที่น้อยกว่าตัวหาร เรียกว่า เศษ
(การหารลงตัวถือว่าเศษเท่ากับ “0”)
ตัวอย่าง 3 17 ÷ 3 = ?
วิธีทำ
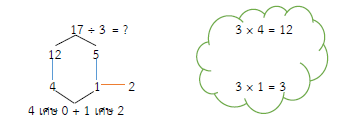
เนื่องจาก (12 + 5) ÷ 3 = ?
? = (12 + 5) ÷ 3
= (12 ÷ 3) + (5 ÷ 3)
= 4 เศษ 0 + 1 เศษ 2
= 5 เศษ 2
ดังนั้น 17 ÷ 3 = 5 เศษ 2
ตอบ 5 เศษ 2
ตรวจคำตอบ
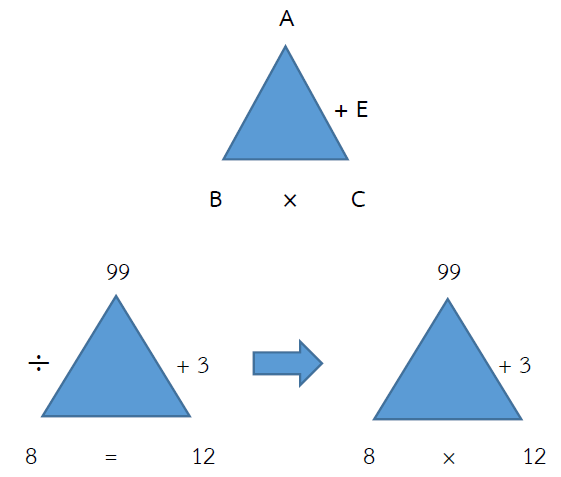
การหารไม่ลงตัว ให้ E = เศษ
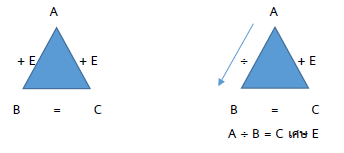
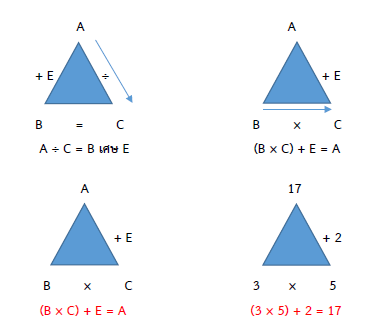
17 ÷ 3 = 5 เศษ 2
กรณีหารไม่ลงตัว จะได้ (B × C) + E = A
ดังนั้น (3 × 5) + 2 = A
15 + 2 = 17
A = 17
จงหาผลหารต่อไปนี้
(1) 75 ÷ 3 = ?
วิธีทำ
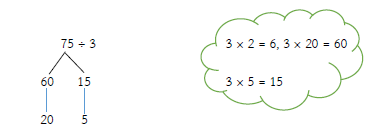
75 ÷ 3 = (60 ÷ 3) + (15 ÷ 3)
= 20 + 5
= 25
ตอบ 25
ตรวจคำตอบ 75 ÷ 3 = 25
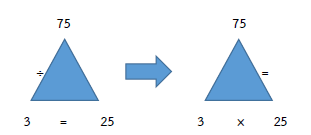
B × C = A , 3 × 25 = 75
แสดงว่าคำตอบถูกต้อง
(2) 82 ÷ 6 = ?
วิธีทำ
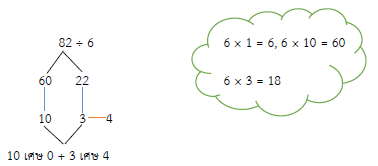
82 ÷ 6 = (60 ÷ 6) + (22 ÷ 6)
= 10 เศษ 0 + 3 เศษ 4
= 13 เศษ 4
ตอบ 13 เศษ 4
ตรวจคำตอบ 82 ÷ 6 = 13 เศษ 4
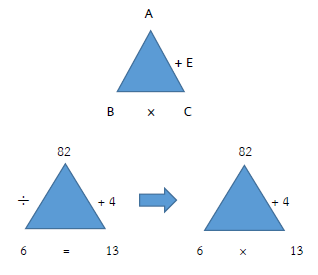
กรณีหารไม่ลงตัว จะได้ (B × C) + เศษ = A
(6 × 13) + 4 = 82
แสดงว่าคำตอบถูกต้อง
(3) 333 ÷ 9 = ?
วิธีทำ
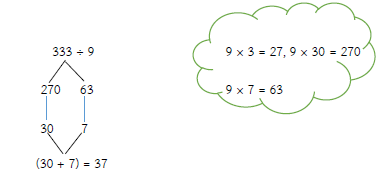
333 ÷ 9 = (270 ÷ 9) + (63 ÷ 9)
= 30 + 7
= 37
ตอบ 37
ตรวจคำตอบ 333 ÷ 9 = 37
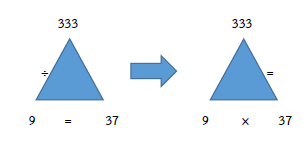
B × C = A หรือ ตัวหารคูณผลหารเท่ากับตัวตั้ง
9 × 37 = 333
แสดงว่าคำตอบถูกต้อง
(4) 675 ÷ 8 = ?
วิธีทำ
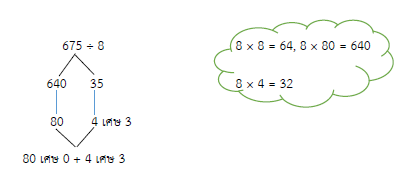
675 ÷ 8 = (640 ÷ 8) + (35 ÷ 8)
= 80 เศษ 0 + 4 เศษ 3
= 84 เศษ 3
ตอบ 84 เศษ 3
ตรวจคำตอบ 675 ÷ 8 = 84 เศษ 3
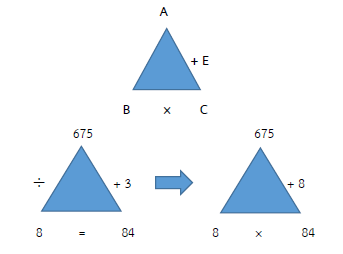
กรณีหารไม่ลงตัว จะได้ (B × C) + เศษ = A
(8 × 84) + 3 = 675
แสดงว่าคำตอบถูกต้อง
แหล่งที่มา
ทรงวิทย์ สุวรรณธาดา และคณะ. (2553). คณิตศาสตร์ ป.3. (ปรับปรุงใหม่). กรุงเทพฯ; บริษัท สำนักพิมพ์แม็ค จำกัด.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2560). คณิตศาสตร์ ชั้นประถมศึกษาปีที่ 3. กรุงเทพฯ; องค์การค้าของ สกสค.
Martha Ruttle. (2010). BRIDGES IN MATHEMATICS Grade 4 Practice Book Blacklines. United States of America : The Math Learning Center.
นิติกร ระดม. 2551. คู่มือครู อจท. คณิตศาสตร์ ป.3. กรุงเทพมหานคร ; อักษรเจริญทัศน์
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. 2551. หนังสือเรียนรายวิชาพื้นฐานคณิตศาสตร์ ป.3.กรุงเทพมหานคร ; องค์การค้าของ สกสค.
Gare, B., & Hoven, J. (2007). Singapore Math Using the Bar Model Approach : Simple or Complex. Educational Leadership. 65 NO 3 November 2007.
Greative Constructions. (2006). FACT FAMILIES. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก http:// greenmonsterlearning.com/pdf/CreativeConstructions.pdf
www.everydaymathonline.com. 4.6 Multiplication and division Fact Families. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://emccss.everydaymathonline.com/em-crosswalk/pdf/3/g3_tlg_lesson_4_6.pdf
www.everydaymathonline.com. 4.6 Multiplication and division Fact Families.สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://emccss.everydaymathonline.com/em-crosswalk/pdf/1/g1_tlg_lesson_6_3.pdf
Math-Drills.com. (2005-2018). fact family worksheets. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://www.math-drills.com/factfamilyworksheets.php
THE BLOG SURGERY. (2018). DIY Math Fact Family Triangles.สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://rainydaymum.co.uk/diy-math-fact-family-triangles/
กลับไปที่เนื้อหา
การหารยาว การหารสั้น
DIY MATH FAMILY TRIANGLES การคูณกับการหาร
A B = C, B × C = A, A C = B
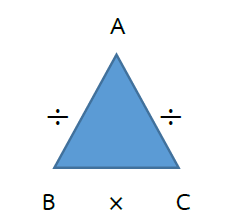
ตรวจคำตอบการหารลงตัว คือ ตัวหารคูณผลหารเท่ากับตัวตั้ง หรือ B × C = A
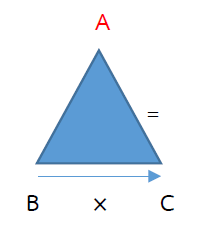
- การหารที่ตัวตั้งสองหลัก ตัวหารและผลมีหนึ่งหลัก
ตัวอย่างที่ 1
56 ÷ 8 = ?
วิธีทำ
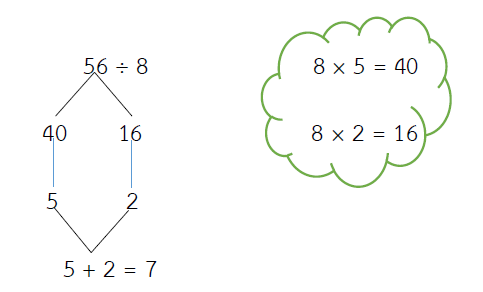
= (40 ÷ 8) + (16 ÷ 8)
= 5 + 2
= 7
ตอบ 7
ตรวจคำตอบ 56 ÷ 8 = 7
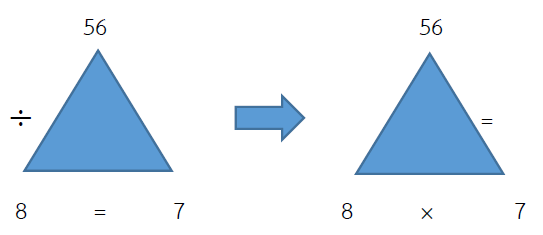
ดังนั้น 8 × 7 = 56
แสดงว่าคำตอบถูกต้อง
ตัวอย่างที่ 2
43 ÷ 9 = ?
วิธีทำ
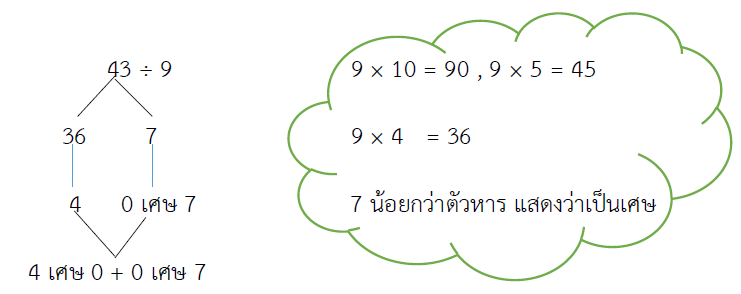
= (36 ÷ 9)
= 4 เศษ 7
ตอบ 4 เศษ 7
ตรวจคำตอบ 43 ÷ 9 = 4 เศษ 7
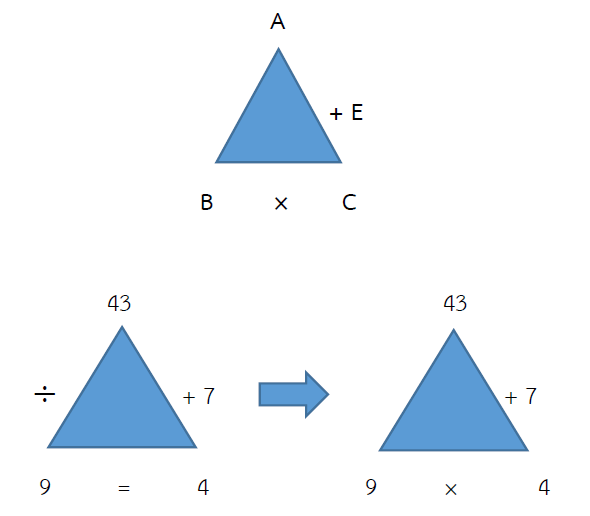
กรณีหารไม่ลงตัว จะได้ (B × C) + เศษ = A
(9 × 4) + 7 = 43
แสดงว่าคำตอบถูกต้อง
- การหารที่ตัวตั้งสองหลัก ตัวหารมีหนึ่งหลักและผลหารมีสองหลัก
ตัวอย่างที่ 1
85 ÷ 7 = ?
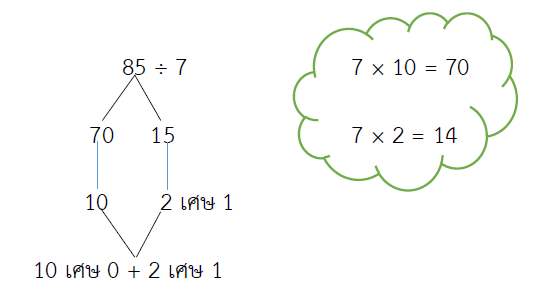
วิธีทำ
= (70 ÷ 7) + (15 ÷ 7)
= 10 เศษ 0 + 2 เศษ 1
= 12 เศษ 1
ตอบ 12 เศษ 1
ตรวจคำตอบ 85 ÷ 7 = 12 เศษ 1
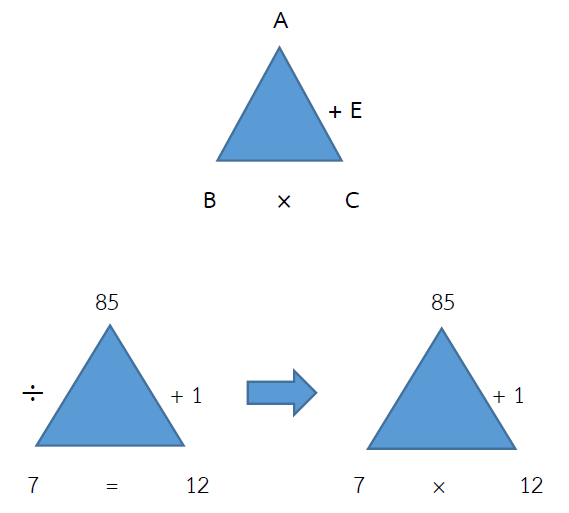
กรณีหารไม่ลงตัว จะได้ (B × C) + เศษ = A
(7 × 12) + 1 = 85
แสดงว่าคำตอบถูกต้อง
ตัวอย่างที่ 2
55 ÷ 5 = ?
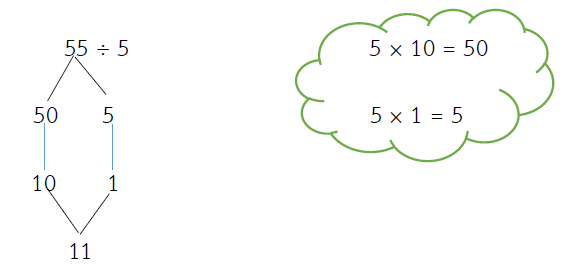
วิธีทำ
= (50 ÷ 5) + (5 ÷ 5)
= 10 + 1
= 11
ตอบ 11
ตรวจคำตอบ 55 ÷ 5 = 11
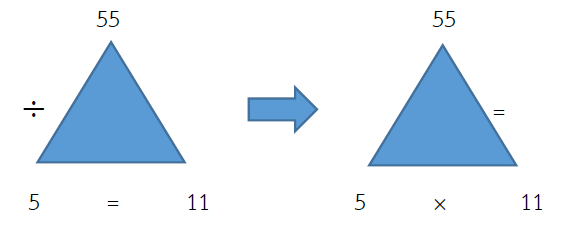
ดังนั้น 5 × 11 = 55
แสดงว่าคำตอบถูกต้อง
- การหารที่ตัวตั้งสามหลัก ตัวหารมีหนึ่งหลัก
ตัวอย่างที่ 1
247 ÷ 7 = ?
วิธีทำ
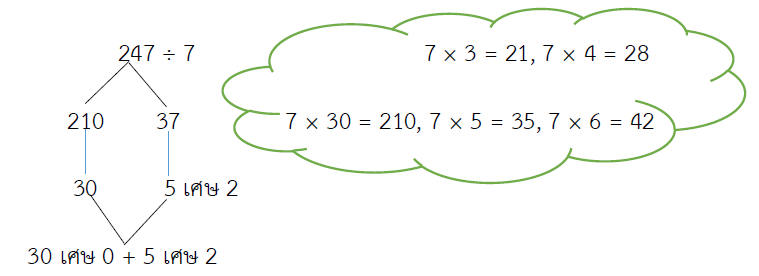
= (210 ÷ 7) + (37 ÷ 7)
= 30 + 5 เศษ 2
= 35 เศษ 2
ตอบ 35 เศษ 2
ตรวจคำตอบ 247 ÷ 7 = 35 เศษ 2
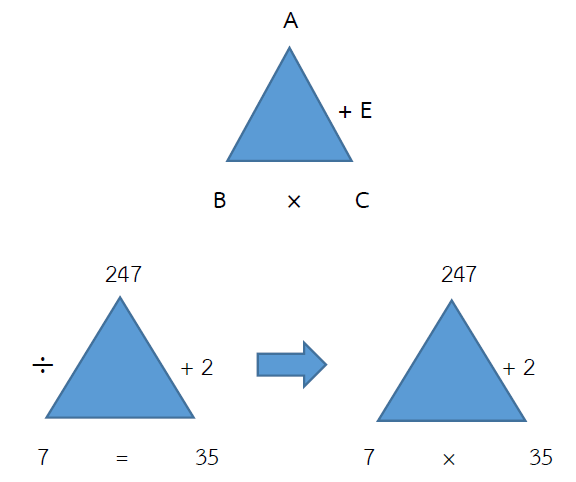
กรณีหารไม่ลงตัว จะได้ (B × C) + เศษ = A
(7 × 35) + 2 = 247
แสดงว่าคำตอบถูกต้อง
ตัวอย่างที่ 2
124 ÷ 4 = ?
วิธีทำ
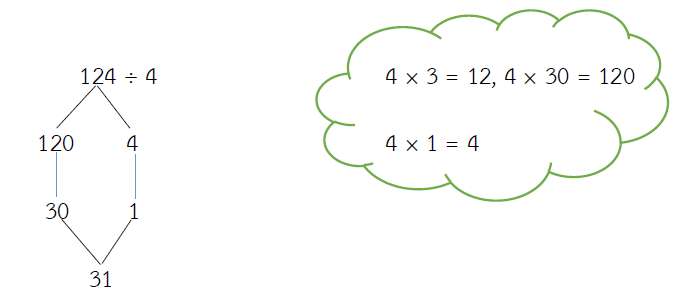
= (120 ÷ 4) + (4 ÷ 4)
= 30 + 1
= 31
ตอบ 31
ตรวจคำตอบ 124 ÷ 4 = 31
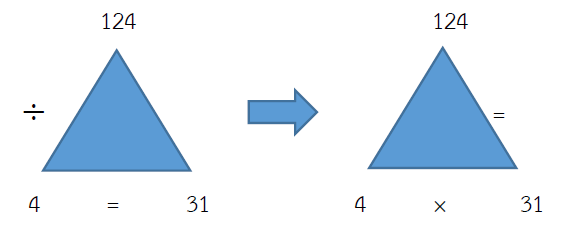
ดังนั้น 4 × 31 = 124
แสดงว่าคำตอบถูกต้อง
- การหารที่ตัวตั้งมีสี่หลัก ตัวหารมีหนึ่งหลัก
ตัวอย่างที่ 1
5,845 ÷ 5 = ?
วิธีทำ
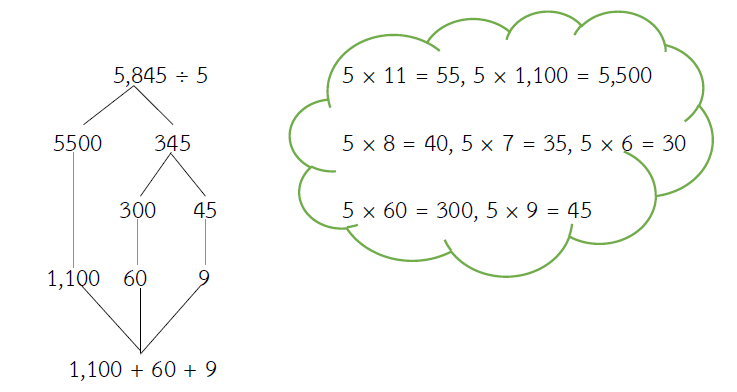
= (5,500 ÷ 5) + (300 ÷ 5) + (45 ÷ 5)
= 1,100 + 60 + 9
= 1,169
ตอบ 1,169
ตรวจคำตอบ 5,845 ÷ 5 = 1,169
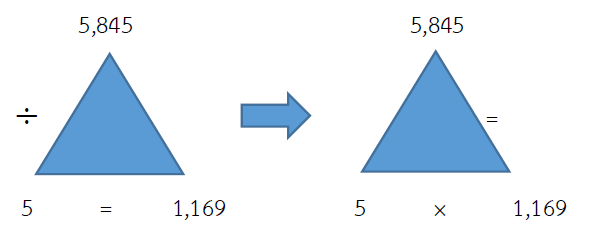
ดังนั้น 5 × 1,169 = 5,845
แสดงว่าคำตอบถูกต้อง
ตัวอย่างที่ 2
6,673 ÷ 6 = ?
วิธีทำ
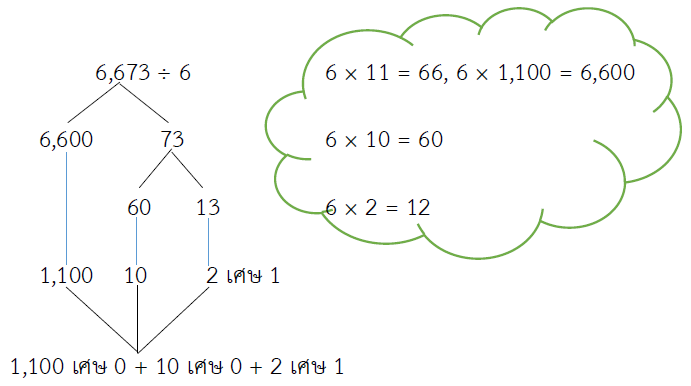
= (6,600 ÷ 6) + (60 ÷ 6) + (13 ÷ 6)
= 1,100 เศษ 0 + 10 เศษ 0 + 2 เศษ 1
= 1,112 เศษ 1
ตอบ 1,112 เศษ 1
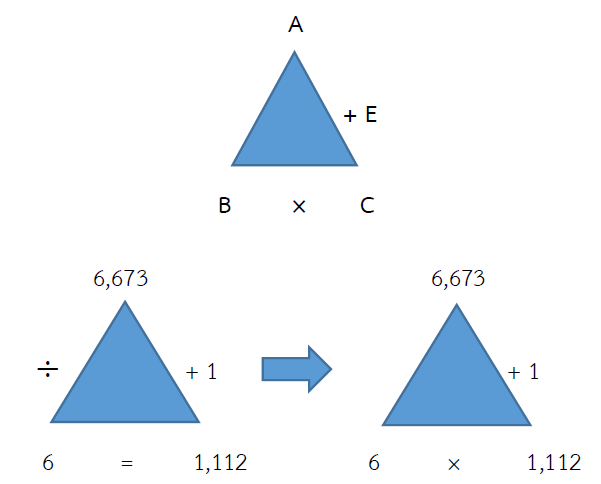
ตรวจคำตอบ 6,673 ÷ 6 = 1,112 เศษ 1
= (ผลหาร × ตัวหาร) + เศษ = ตัวตั้ง
= (1,112 × 6) + 1 = 6,673
การหารสั้น
- การหารที่ตัวตั้งสองหลัก ตัวหารและผลมีหนึ่งหลัก
ตัวอย่างที่ 1
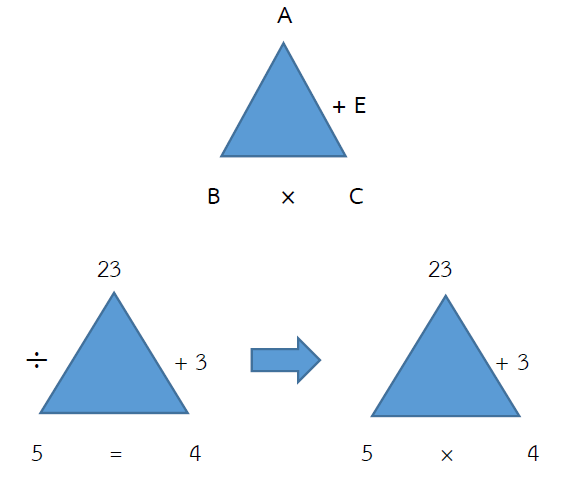
23 ÷ 5 = ?
วิธีทำ
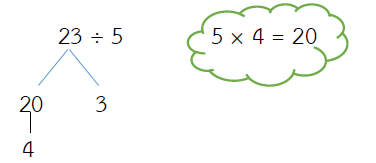
ตอบ 4 เศษ 3
ตรวจคำตอบ 23 ÷ 5 = 4 เศษ 3
= (ผลหาร × ตัวหาร) + เศษ = ตัวตั้ง
= (4 × 5) + 3 = 23
ตัวอย่างที่ 2
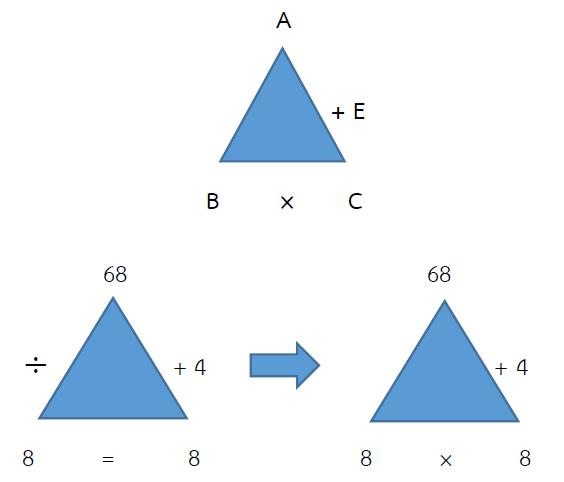
68 ÷ 8 = ?
วิธีทำ
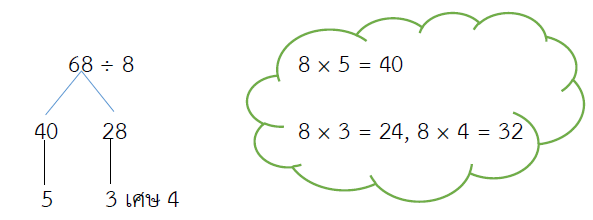
ตอบ 8 เศษ 4
ตรวจคำตอบ 68 ÷ 8 = 8 เศษ 4
= (ผลหาร × ตัวหาร) + เศษ = ตัวตั้ง
= (8 × 8) + 4 = 68
- การหารที่ตัวตั้งสองหลัก ตัวหารมีหนึ่งหลักและผลหารมีสองหลัก
ตัวอย่างที่ 1
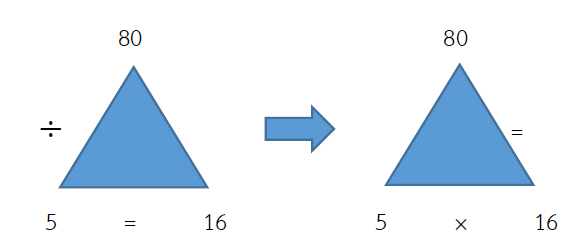
80 ÷ 5 = ?
วิธีทำ
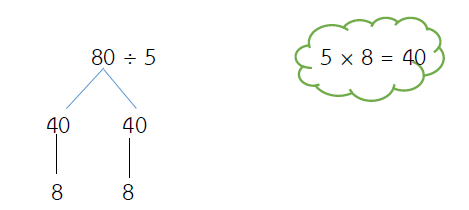
ตอบ 16
ตรวจคำตอบ 80 ÷ 5 = 16
= (ผลหาร × ตัวหาร) = ตัวตั้ง
= (16 × 5) = 80
ตัวอย่างที่ 2
99 ÷ 8 = ?
วิธีทำ
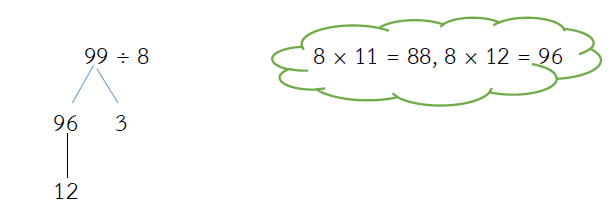
ตอบ 12 เศษ 3
ตรวจคำตอบ 99 ÷ 8 = 12 เศษ 3
= (ผลหาร × ตัวหาร) + เศษ = ตัวตั้ง
= (12 × 8) + 3 = 99
- การหารที่ตัวตั้งสามหลัก ตัวหารมีหนึ่งหลัก
ตัวอย่างที่ 1
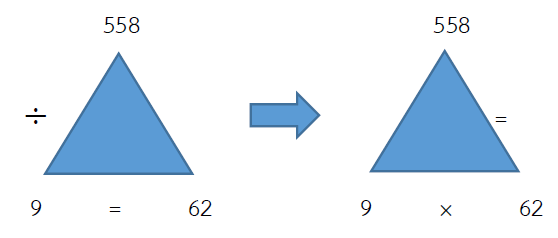
558 ÷ 9 = ?
วิธีทำ
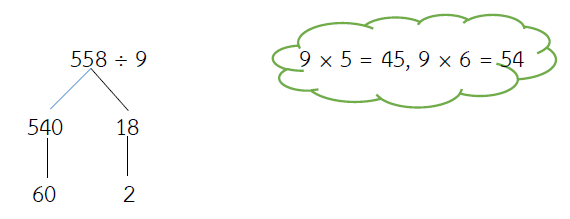
ตอบ 62
ตรวจคำตอบ 558 ÷ 9 = 62
= (ผลหาร × ตัวหาร) = ตัวตั้ง
= (62 × 9) = 558
ตัวอย่างที่ 2
267 ÷ 3 = ?
วิธีทำ
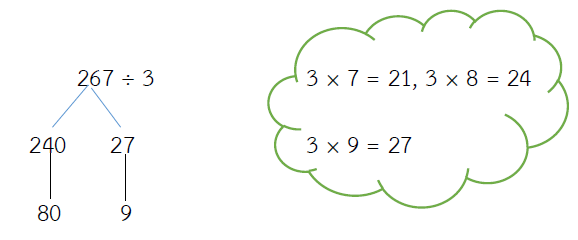
ตอบ 89
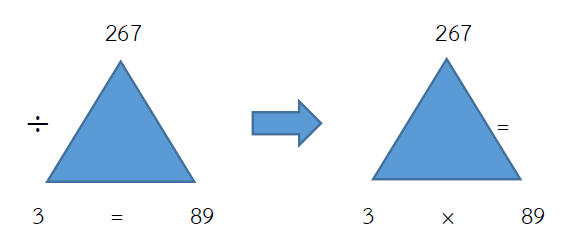
ตรวจคำตอบ 267 ÷ 3 = 89
= (ผลหาร × ตัวหาร) = ตัวตั้ง
= (89 × 3) = 267
- การหารที่ตัวตั้งมีสี่หลัก ตัวหารมีหนึ่งหลัก
ตัวอย่างที่ 1
7,324 ÷ 8 = ?
วิธีทำ
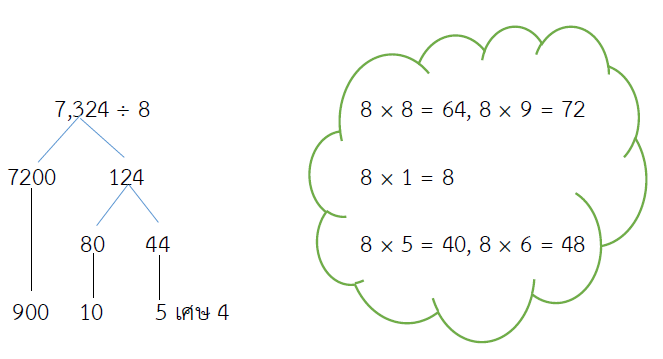
ตอบ 915 เศษ 4
ตรวจคำตอบ 7,324 ÷ 8 = 915 เศษ 4
= (ผลหาร × ตัวหาร) + เศษ = ตัวตั้ง
= (915 × 8) + 4 = 7,324
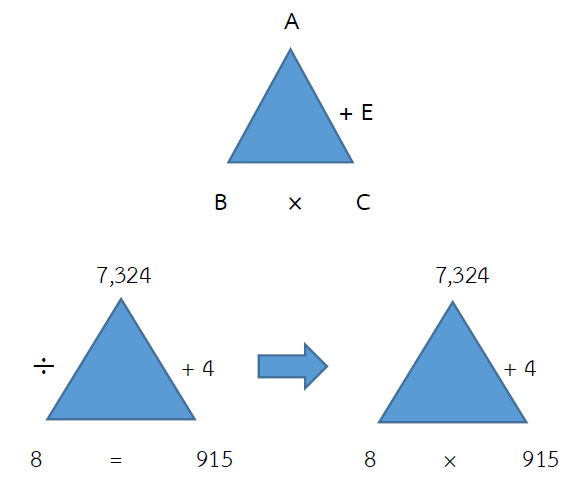
ตัวอย่างที่ 2
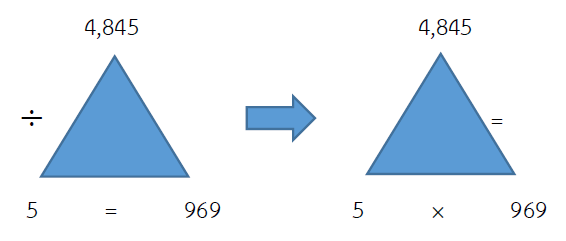
4,845 ÷ 5 = ?
วิธีทำ
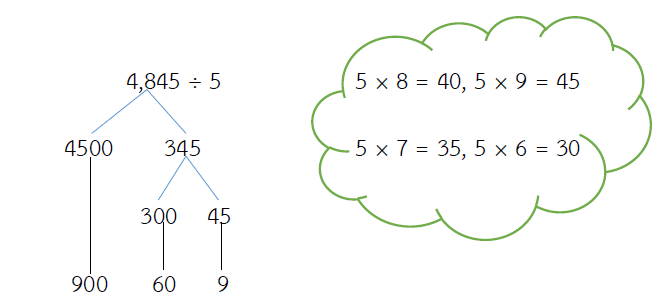
ตอบ 969
ตรวจคำตอบ 4,845 ÷ 5 = 969
= (ผลหาร × ตัวหาร) = ตัวตั้ง
= (969 × 5) = 4,845
แหล่งที่มา
ทรงวิทย์ สุวรรณธาดา และคณะ. (2553). คณิตศาสตร์ ป.3. (ปรับปรุงใหม่). กรุงเทพฯ; บริษัท สำนักพิมพ์แม็ค จำกัด.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2560). คณิตศาสตร์ ชั้นประถมศึกษาปีที่ 3. กรุงเทพฯ; องค์การค้าของ สกสค.
Martha Ruttle. (2010). BRIDGES IN MATHEMATICS Grade 4 Practice Book Blacklines. United States of America : The Math Learning Center.
นิติกร ระดม. 2551. คู่มือครู อจท. คณิตศาสตร์ ป.3. กรุงเทพมหานคร ; อักษรเจริญทัศน์
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. 2551. หนังสือเรียนรายวิชาพื้นฐานคณิตศาสตร์ ป.3.กรุงเทพมหานคร ; องค์การค้าของ สกสค.
Gare, B., & Hoven, J. (2007). Singapore Math Using the Bar Model Approach : Simple or Complex. Educational Leadership. 65 NO 3 November 2007.
Greative Constructions. (2006). FACT FAMILIES. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก http:// greenmonsterlearning.com/pdf/CreativeConstructions.pdf
www.everydaymathonline.com. 4.6 Multiplication and division Fact Families. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://emccss.everydaymathonline.com/em-crosswalk/pdf/3/g3_tlg_lesson_4_6.pdf
www.everydaymathonline.com. 4.6 Multiplication and division Fact Families.สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://emccss.everydaymathonline.com/em-crosswalk/pdf/1/g1_tlg_lesson_6_3.pdf
Math-Drills.com. (2005-2018). fact family worksheets. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://www.math-drills.com/factfamilyworksheets.php
THE BLOG SURGERY. (2018). DIY Math Fact Family Triangles.สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://rainydaymum.co.uk/diy-math-fact-family-triangles/
กลับไปที่เนื้อหา
โจทย์ปัญหาการหาร
ความหมายของการหาร
- เมื่อนำจำนวนหนึ่งจำนวนมาแบ่งเป็นกลุ่ม กลุ่มละเท่า ๆ กัน ต้องการหาว่าแบ่งได้กี่กลุ่ม ทำได้ด้วยการหาร เช่น ครูมีนักเรียน 6 คน เข้ากลุ่ม กลุ่มละ 2 คน จัดได้กี่กลุ่ม
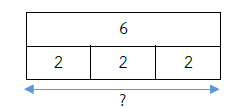
ครูจัดนักเรียน 6 คน เข้ากลุ่ม กลุ่มละ 2 คน ได้ 3 กลุ่ม
เขียนในรูปการหารด้วย 6 ÷ 2 = 3
เรียก 3 ว่าผลหาร ซึ่งแสดงจำนวนกลุ่ม
- ผลหารแสดงจำนวนสิ่งของในกลุ่ม หรือจำนวนกลุ่มของสิ่งของ เช่น ครูจัดนักเรียน 6 คน เข้ากลุ่ม 2 กลุ่มละเท่า ๆ กัน ได้กลุ่มละกี่คน
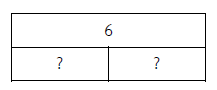
2
ครูจัดนักเรียน 6 คน เข้ากลุ่ม 2 กลุ่ม กลุ่มละเท่า ๆ กัน ได้กลุ่มละ 3 คน
เขียนในรูปการหารด้วย 6 ÷ 2 = 3
เรียก 3 ว่าผลหาร ซึ่งแสดงจำนวนสิ่งของในกลุ่ม
ตัวอย่างที่ 1
ครูมีเงิน 280 บาท ซื้อขนมเพื่อแจกเด็กห่อละ 9 บาท ครูจะซื้อขนมได้ทั้งหมดกี่ห่อ และเหลือเงินกี่บาท
วิเคราะห์โจทย์ปัญหา
- ครูมีเงิน 280 บาท
- ซื้อขนมเพื่อแจกเด็กห่อละ 9 บาท
- ครูจะซื้อขนมได้ทั้งหมดกี่ห่อ
- เหลือเงินกี่บาท
ขนม 1 ห่อ = 9 บาท
ขนม 10 ห่อ = 90 บาท
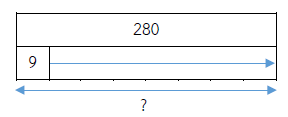
ประโยคสัญลักษณ์ 280 ÷ 9 = ?
วิธีทำ
ครูมีเงิน 280 บาท
ซื้อขนมเพื่อแจกเด็กห่อละ 9 บาท
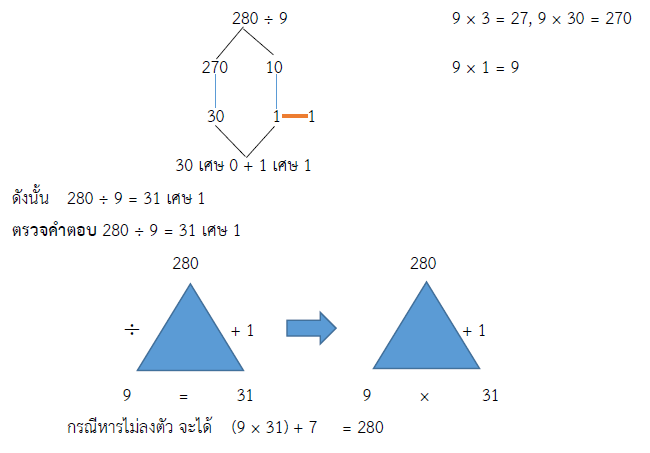
เนื่องจาก 280 ÷ 9 = 31 เศษ 1
ดังนั้น ครูจะซื้อขนมได้ทั้งหมด 31 ห่อ เหลือเงิน 1 บาท
ตอบ 31 ห่อ เหลือเงิน 1 บาท
วิธีคิด 280 ÷ 9 = ?
ตัวอย่างที่ 2
ตุ๊กซื้อเสื้อแบบเดียวกัน 7 ตัว เป็นเงิน 1,750 บาท ตุ๊กซื้อเสื้อราคาตัวละกี่บาท
วิเคราะห์โจทย์ปัญหา
- ตุ๊กซื้อเสื้อแบบเดียวกัน 7 ตัว
- เป็นเงิน 1,750 บาท
- ตุ๊กซื้อเสื้อราคาตัวละกี่บาท
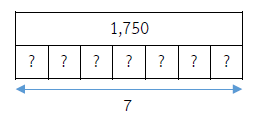
ประโยคสัญลักษณ์ 1,750 ÷ 7 = ?
วิธีทำ
ตุ๊กซื้อเสื้อแบบเดียวกัน 7 ตัว
เป็นเงิน 1,750 บาท
เนื่องจาก 1,750 ÷ 7 = 250
ดังนั้น ตุ๊กซื้อเสื้อราคาตัวละ 250 บาท
ตอบ 250 บาท
วิธีคิด 1,750 ÷ 7 = ?
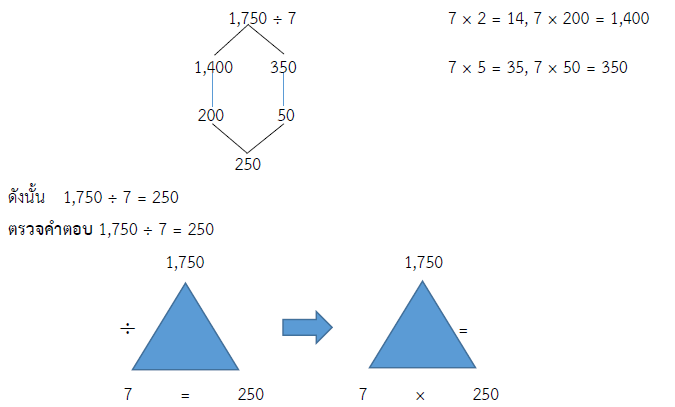
ดังนั้น 7 × 250 = 1,750
ตัวอย่างที่ 3.
แม่มีดอกบัว 30 ดอก มัดเป็นกำ กำละ 5 ดอก จะได้กี่กำ
วิเคราะห์โจทย์ปัญหา
- แม่มีดอกบัว 30 ดอก
- กำละ 5 ดอก
- จะได้กี่กำ
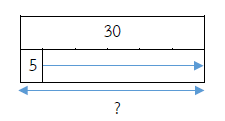
ประโยคสัญลักษณ์ 30 ÷ 5 = ?
วิธีทำ
แม่มีดอกบัว 30 ดอก
มัดเป็นกำ กำละ 5 ดอก
เนื่องจาก 30 ÷ 5 = 6
ดังนั้น แม่มีดอกบัว มัดเป็นกำ ได้ 6 กำ
ตอบ 6 กำ
ตรวจคำตอบ 30 ÷ 5 = 6
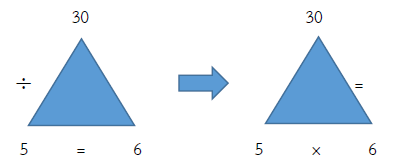
ดังนั้น 5 × 6 = 30
ตัวอย่างที่ 4.
ป้ามีที่ดิน 750 ตารางวา แบ่งออกเป็น 5 แปลง แปลงละเท่า ๆ กัน จะแบ่งที่ดินได้แปลงละกี่ตารางวา
วิเคราะห์โจทย์ปัญหา
- ป้ามีที่ดิน 750 ตารางวา
- แบ่งออกเป็น 5 แปลง แปลงละเท่า ๆ กัน
- จะแบ่งที่ดินได้แปลงละกี่ตารางวา
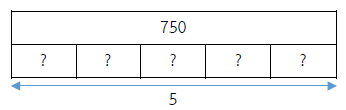
ประโยคสัญลักษณ์ 750 ÷ 5 = ?
วิธีทำ
ป้ามีที่ดิน 750 ตารางวา
แบ่งออกเป็น 5 แปลง แปลงละเท่า ๆ กัน
เนื่องจาก 750 ÷ 5 = 150
จะแบ่งที่ดินได้แปลงละ 150 ตารางวา
ตอบ 150 ตารางวา
วิธีคิด 750 ÷ 5 = ?
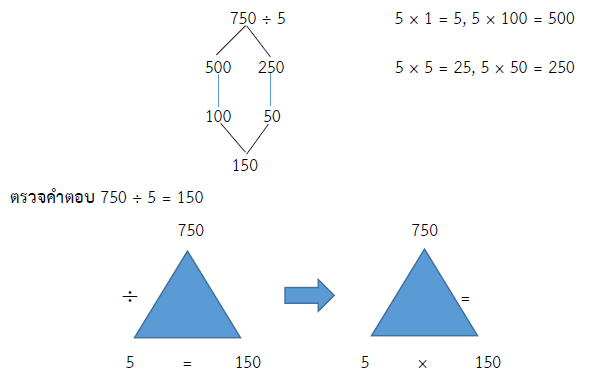
ดังนั้น 5 × 150 = 750
ตัวอย่างที่ 5.
หน่องมีสติกเกอร์ 2,150 รูป นำไปใส่ซอง ซองละ 6 รูป จะต้องใช้ซองกี่ซอง และเหลือสติกเกอร์กี่รูป
วิเคราะห์โจทย์ปัญหา
- หน่องมีสติกเกอร์ 2,150 รูป
- นำไปใส่ซอง ซองละ 6 รูป
- จะต้องใช้ซองกี่ซอง เหลือสติกเกอร์กี่รูป
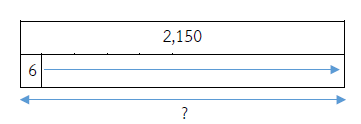
ประโยคสัญลักษณ์ 2,150 ÷ 6 = ?
วิธีทำ
หน่องมีสติกเกอร์ 2,150 รูป
นำไปใส่ซอง ซองละ 6 รูป
เนื่องจาก 2,150 ÷ 6 = 358 เศษ 2
ดังนั้น ต้องใช้ซอง 358 ซอง และเหลือสติกเกอร์ 2 รูป
ตอบ 358 ซอง เหลือสติกเกอร์ 2 รูป
วิธีคิด 2,150 ÷ 6 = ?
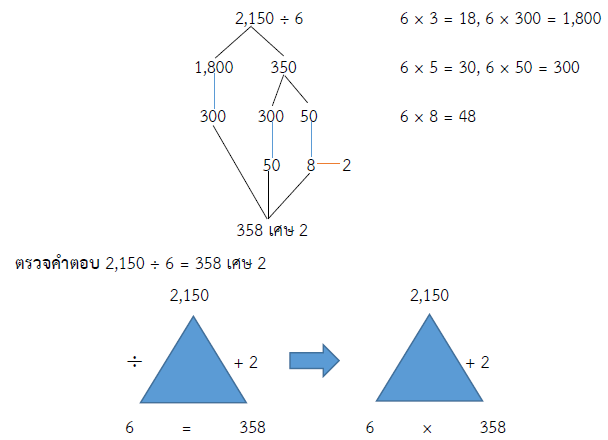
กรณีหารไม่ลงตัว จะได้ (6 × 358) + 2 = 2,150
ตัวอย่างที่ 6.
ขวัญเลี้ยงปลาทองไว้ 570 ตัว แบ่งใส่อ่าง อ่างละ 95 ตัว จะได้กี่อ่าง
วิเคราะห์โจทย์ปัญหา
- ขวัญเลี้ยงปลาทองไว้ 570 ตัว
- แบ่งใส่อ่าง อ่างละ 95 ตัว
- จะได้กี่อ่าง
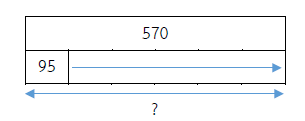
ประโยคสัญลักษณ์ 570 ÷ 95 = ?
วิธีทำ
ขวัญเลี้ยงปลาทองไว้ 570 ตัว
แบ่งใส่อ่าง อ่างละ 95 ตัว
เนื่องจาก 570 ÷ 95 = 6
ดังนั้น ขวัญแบ่งปลาทองใส่อ่าง ได้ 6 อ่าง
ตอบ 6 อ่าง
วิธีคิด 570 ÷ 95 = ?
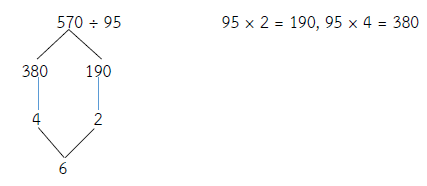
ดังนั้น 570 ÷ 95 = 6
ตรวจคำตอบ 570 ÷ 95 = 6
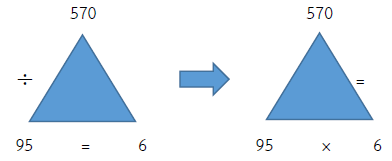
ดังนั้น 95 × 6 = 570
ตัวอย่างที่ 7.
ถ้าแม่มีเงิน 2,560 บาท แบ่งให้ลูกคนละ 640 บาท เท่ากันทุกคน แม่จะแบ่งเงินทั้งหมดให้ลูกกี่คน
วิเคราะห์โจทย์
- ถ้าแม่มีเงิน 2,560 บาท
- แบ่งให้ลูกคนละ 640 บาท เท่ากันทุกคน
- แม่จะแบ่งเงินทั้งหมดให้ลูกกี่คน

ประโยคสัญลักษณ์ 2,560 ÷ 640 = ?
วิธีทำ
แม่มีเงิน 2,560 บาท
แบ่งให้ลูกคนละ 640 บาท เท่ากันทุกคน
เนื่องจาก 2,560 ÷ 640 = 4
แม่จะแบ่งเงินทั้งหมดให้ลูก 4 คน
ตอบ 4 คน
วิธีคิด 2,560 ÷ 640 = ?
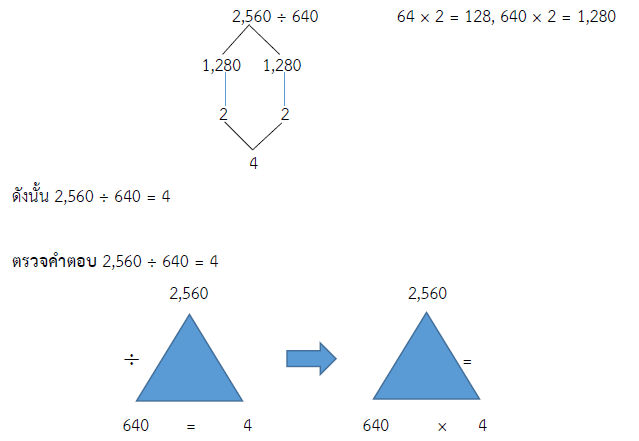
ดังนั้น 640 × 4 = 2,560
แหล่งที่มา
ทรงวิทย์ สุวรรณธาดา และคณะ. (2553). คณิตศาสตร์ ป.3. (ปรับปรุงใหม่). กรุงเทพฯ; บริษัท สำนักพิมพ์แม็ค จำกัด.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2560). คณิตศาสตร์ ชั้นประถมศึกษาปีที่ 3. กรุงเทพฯ; องค์การค้าของ สกสค.
Martha Ruttle. (2010). BRIDGES IN MATHEMATICS Grade 4 Practice Book Blacklines. United States of America : The Math Learning Center.
นิติกร ระดม. 2551. คู่มือครู อจท. คณิตศาสตร์ ป.3. กรุงเทพมหานคร ; อักษรเจริญทัศน์
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. 2551. หนังสือเรียนรายวิชาพื้นฐานคณิตศาสตร์ ป.3.กรุงเทพมหานคร ; องค์การค้าของ สกสค.
Gare, B., & Hoven, J. (2007). Singapore Math Using the Bar Model Approach : Simple or Complex. Educational Leadership. 65 NO 3 November 2007.
Greative Constructions. (2006). FACT FAMILIES. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก http:// greenmonsterlearning.com/pdf/CreativeConstructions.pdf
www.everydaymathonline.com. 4.6 Multiplication and division Fact Families. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://emccss.everydaymathonline.com/em-crosswalk/pdf/3/g3_tlg_lesson_4_6.pdf
www.everydaymathonline.com. 4.6 Multiplication and division Fact Families.สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://emccss.everydaymathonline.com/em-crosswalk/pdf/1/g1_tlg_lesson_6_3.pdf
Math-Drills.com. (2005-2018). fact family worksheets. สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://www.math-drills.com/factfamilyworksheets.php
THE BLOG SURGERY. (2018). DIY Math Fact Family Triangles.สืบค้นเมื่อ 5 ธันวาคม 2561, จาก https://rainydaymum.co.uk/diy-math-fact-family-triangles/
กลับไปที่เนื้อหา



