แรงและเวกเตอร์ของแรง
ในการศึกษาในวิชาฟิสิกส์พบว่า มีความเกี่ยวข้องกับปริมาณต่าง ๆ มากมาย โดยปริมาณเหล่านั้นจะแบ่งได้ 2 พวกใหญ่ ๆ เช่นเชียงใหม่อยู่ห่างจากกรุงเทพมหานคร 720 กิโลเมตร หมายความว่าถ้าเดินทางไปตามถนนจากกรุงเทพมหานครไปยังเชียงใหม่พบว่าอาจเดินหลงไปจังหวัดอื่นก็ได้เพราะไม่รู้ทิศทางที่ถูกต้อง ดังนั้นถ้าจะให้เดินถูกทางต้องบอกทิศทางการเคลื่อนที่ด้วย และแนวการเคลื่อนที่ก็มีผลต่อระยะการเคลื่อนที่ด้วย เช่น เดินทางเป็นเส้นตรงจากกรุงเทพมหานครไปเชียงใหม่จะได้ระยะการเคลื่อนที่น้อยกว่าระยะการเคลื่อนที่ตามถนน เพราะถนนมีการเลี้ยวไปมาทำให้ระยะทางการเคลื่อนที่มากกว่าระยะห่างซึ่งจากตัวอย่างที่กล่าวมาจะเห็นได้ว่าปริมาณบางปริมาณบอกแต่ขนาดก็ได้ความสมบูรณ์แล้วแต่บางปริมาณต้องบอกถึงทิศทางประกอบด้วยจึงจะสมบูรณ์ ปริมาณทางฟิสิกส์จึงแบ่งออกเป็น 2 ประเภท ดังนี้
-
ปริมาณสเกลาร์ (Scalar quantity) คือ ปริมาณที่มีเพียงขนาดอย่างเดียว โดยสามารถบอกแต่ขนาดอย่างเดียวก็ได้ความหมายสมบูรณ์ ไม่ต้องบอกทิศทาง เช่น ระยะทาง มวล เวลา ปริมาตร งาน พลังงาน ความหนาแน่น อุณหภูมิ พื้นที่ อัตราเร็ว ฯลฯ และการหาผลลัพธ์ของปริมาณสเกลาร์ก็อาศัยหลักการทางพีชคณิต คือ วิธีการ บวก ลบ คูณ หาร
-
ปริมาณเวกเตอร์ (Vector quantity) คือ ปริมาณที่มีทั้งขนาด และทิศทาง โดยเป็นปริมาณที่ต้องบอกทั้งขนาดและทิศทางจึงจะได้ความหมายสมบูรณ์ เช่น การกระจัด ความเร็ว ความเร่ง แรง โมเมนตัม น้ำหนัก โมเมนต์ ฯลฯ การรวมกันของปริมาณเวกเตอร์ต้องพิจารณาทั้งขนาดและทิศทาง นั่นก็คือการหาผลลัพธ์ของปริมาณเวกเตอร์ต้องอาศัยวิธีการทางเวกเตอร์โดยต้องหาผลลัพธ์ทั้งขนาดและทิศทาง

ภาพ การเคลื่อนที่ของรถบนถนน
ที่มา https://pixabay.com/photos/road-car-motion-vehicle-auto-1610959/, Skitterphoto
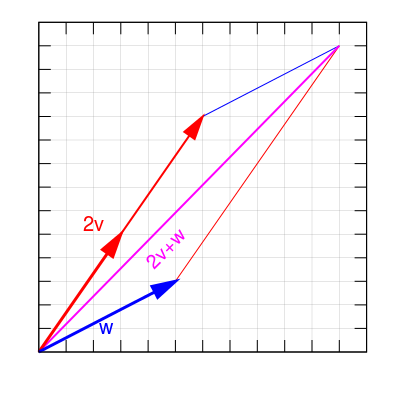
ภาพ Vector scalar multiplication
ที่มา https://commons.wikimedia.org/wiki/File:Vector_scalar_multiplication.svg ,G4spr0m
ตัวอย่างที่ 1 รถคันหนึ่งวิ่งด้วยความเร็ว 60 กิโลเมตรต่อชั่วโมงไปทางทิศเหนือ
60 คือ ขนาดของความเร็ว นั่นคือการแสดงให้เห็นถึงการมีขนาด
ทิศเหนือ คือทิศของความเร็ว นั่นคือการแสดงให้เห็นถึงการมีทิศทาง
กิโลเมตรต่อชั่วโมง คือ หน่วยของความเร็ว
ดังนั้น ความเร็วจึงเป็นปริมาณเวกเตอร์
ตัวอย่างที่ 2 ขณะนี้เป็นเวลา 8.00 น.
8.00 คือ ขนาดของเวลา นั่นคือการแสดงให้เห็นถึงการมีขนาด แต่ไม่มีทิศทาง
น. คือ หน่วยของเวลา
ดังนั้น เวลาจึงเป็นปริมาณสเกลาร์
ตัวอย่างที่ 3 ปริมาณในทางฟิสิกส์ที่บอกให้ทราบว่าวัตถุมีความเฉื่อยมากหรือน้อยคือข้อใด
-
ความเร่ง 2. มวล 3. แรง 4. น้ำหนัก
เฉลย คำตอบที่ถูกต้องคือข้อ 2 เพราะปริมาณที่บอกให้ทราบว่าวัตถุมีความเฉื่อยมากหรือน้อยคือมวล
ตัวอย่างที่ 4 ปริมาณทางฟิสิกส์ถ้าจัดแบ่งโดยอาศัยทิศทางจะแบ่งได้เป็นปริมาณใดบ้าง
-
ปริมาณเวกเตอร์, ปริมาณสเกลาร์
-
ปริมาณเชิงคุณภาพ, ปริมาณเชิงปริมาณ
-
ปริมาณเชิงบรรยาย, ปริมาณเชิงคำนวณ
-
ปริมาณฐาน,ปริมาณอนุพัทธ์
เฉลย คำตอบที่ถูกต้องคือข้อ1 เพราะปริมาณทางฟิสิกส์ อาจจัดแบ่งโดยอาศัยทิศทางจะแบ่งได้ 2 ปริมาณ คือปริมาณเวกเตอร์ปริมาณสเกลาร์
ตัวอย่างที่ 5 ปริมาณในข้อใดต่อไปนี้เป็นปริมาณประเภทเดียวกันทั้งหมด
-
การกระจัด, ความเร็ว, เวลา
-
แรง, ความเร่ง,สนามไฟฟ้า
-
มวล, แรง, ความเร่ง
-
อัตราเร็ว, เวลา, โมเมตัม
เฉลย คำตอบที่ถูกต้องคือข้อ2 เพราะว่าจากโจทย์ต้องการหาในตัวเลือกในข้อใดเป็นปริมาณประเภทเดียวกัน โดย
ข้อ 1 การกระจัด,ความเร็วเป็นปริมาณเวกเตอร์ ส่วนเวลาเป็นปริมาณสเกลาร์ ดังนั้นข้อ 1 ผิด
ข้อ 2 แรง,ความเร่งและสนามไฟฟ้า เป็นปริมาณเวกเตอร์ทั้งหมด ดังนั้นข้อ 2 ถูก
ข้อ 3 มวลเป็นปริมาณสเกลาร์ส่วนแรง,ความเร่งเป็นปริมาณเวกเตอร์ดังนั้นข้อ 3 ผิด
ข้อ 4 อัตราเร็ว,เวลาเป็นปริมาณสเกลาร์ ส่วนโมเมนตัมเป็นปริมาณเวกเตอร์ ดังนั้นข้อ 4 ผิด
ตัวอย่างที่ 6 ปริมาณในข้อใดเป็นปริมาณสเกลาร์ทั้งหมด
-
ความเร็ว, เวลา,การกระจัด 2. อัตราเร็ว,เวลา,ระยะทาง
-
ความดัน,ความเร่ง,ความหนาแน่น 4. สนามแม่เหล็ก,สนามไฟฟ้า,สนามความโน้มถ่วง
เฉลย คำตอบที่ถูกต้องคือข้อ 2 โจทย์ต้องการหาตัวเลือกใดเป็นปริมาณสเกลาร์ทั้งหมดให้พิจารณาทีละตัวเลือก
ข้อ 1 เวลาเป็นปริมาณสเกลาร์ แต่ความเร็ว,การกระจัดเป็นปริมาณเวกเตอร์ ดังนั้นข้อ 1 ผิด
ข้อ 2 อัตราเร็ว,เวลา,ระยะทาง ทุกปริมาณเป็นปริมาณสเกลาร์ทั้งหมด ดังนั้นข้อ 2 ถูก
ข้อ 3ความดัน,ความหนาแน่น เป็นปริมาณสเกลาร์ แต่ความเร่งเป็นปริมาณเวกเตอร์ ดังนั้ข้อ 3 ผิด
ข้อ 4 สนามแม่เหล็ก,สนามไฟฟ้าและสนามความโน้มถ่วง ทุกปริมาณเป็นปริมาณเวกเตอร์ทั้งหมด ดังนั้นข้อ 4 ผิด
ตัวอย่างที่ 7 ปริมาณในข้อใดเป็นปริมาณเวกเตอร์ทั้งหมด
-
ความเร็ว, เวลา, การกระจัด
-
อัตราเร็ว, เวลา, ระยะทาง
-
ความดัน, ความเร่ง, ความหนาแน่น
-
การกระจัด, สนามไฟฟ้า, แรง
เฉลย คำตอบที่ถูกต้องคือข้อ 4 โจทย์ต้องการหาตัวเลือกใดเป็นปริมาณเวกเตอร์ทั้งหมดให้พิจารณาทีละตัวเลือก
ข้อ 1 เวลาเป็นปริมาณสเกลาร์ แต่ความเร็ว,การกระจัดเป็นปริมาณเวกเตอร์ ดังนั้นข้อ 1 ผิด
ข้อ 2 อัตราเร็ว,เวลา,ระยะทาง ทุกปริมาณเป็นปริมาณสเกลาร์ทั้งหมด ดังนั้นข้อ 2 ผิด
ข้อ 3 ความดัน,ความหนาแน่น เป็นปริมาณสเกลาร์ แต่ความเร่งเป็นปริมาณเวกเตอร์ ดังนั้นข้อ 3 ผิด
ข้อ 4 การกระจัด,สนามไฟฟ้า, แรง ทุกปริมาณเป็นปริมาณเวกเตอร์ทั้งหมด ดังนั้นข้อ 4 ถูก
ตัวอย่างที่ 8 ข้อความใดต่อไปนี้เป็นปริมาสเกลาร์ และข้อใดเป็นปริมาณเวกเตอร์
8.1 เดินทางได้ระยะทาง 3 กิโลเมตร
เฉลย ปริมาณสเกลาร์ เพราะบอกแต่ขนาดไม่บอกทิศทาง
8.2 เดินทางตรงไป 3 กิโลเมตร ในทิศตะวันออก
เฉลย ปริมาณเวกเตอร์ เพราะบอกทั้งขนาดและทิศทาง
8.3 ลูกบอลเคลื่อนที่ไปใช้เวลา 30 วินาที
เฉลย ปริมาณสเกลาร์ เพราะบอกแต่ขนาดไม่บอกทิศทาง
8.4 ขับรถยนต์ด้วยอัตราเร็ว 80 กิโลเมตรต่อชั่วโมง
เฉลย ปริมาณสเกลาร์ เพราะบอกแต่ขนาดไม่บอกทิศทาง
8.5 ขับรถยนต์ด้วยความเร็ว 80 กิโลเมตรต่อชั่วโมง ไปในทิศใต้
เฉลย ปริมาณเวกเตอร์ เพราะบอกทั้งขนาดและทิศทาง
แหล่งที่มา
จรัญ บุระตะ. (2555). ฟิสิกส์ เล่ม 1 ม. 4-6. กรุงเทพฯ:นิพนธ์.
สุธาธรรม ชลบุรี และคณะ.(2537). ฟิสิกส์ เล่ม 1 ม. 4. กรุงเทพฯ:ภูมิบัณฑิต.
อนุสรณ์ แสนวงศ์.(มมป). ปริมาณทางฟิสิกส์. สืบค้นเมื่อ 15 สิงหาคม 2562, จาก
https://sites.google.com/site/anusorn2368/hnwy-thi-1/priman-thang-fisiks
กลับไปที่เนื้อหา
ปริมาณเวกเตอร์ คือ ปริมาณที่มีทั้งขนาดและทิศทาง เราจะบอกเพียงแค่ขนาดหรือทิศทางอย่างใดอย่างหนึ่งไม่ได้ เราต้องระบุทั้งขนาดและทิศทางจึงจะเรียกว่า เวกเตอร์ เพราะการระบุแค่ขนาดหรือทิศทางอย่างใดอย่างหนึ่งนั้นจะทำให้การสื่อความหมายอาจไม่ตรงกัน เช่น ครูออกคำสั่งกับนักเรียนทุกคนว่า “ให้นักเรียนทุกคนลุกขึ้นจากเก้าอี้แล้วเดินไปคนละ 5 เมตร” เหตุการณ์ที่เกิดขึ้นคือ นักเรียนทุกคนเดินไปคนละ 5 เมตร แต่ว่านักเรียนแต่ละคนก็จะเดินไปคนละทิศทาง เพราะไม่รู้ว่าครูสั่งให้เดินไปทางไหน เพราะคำสั่งของครูมีแต่ขนาด คือ 5 เมตร แต่ขาดทิศทางซึ่งก็ถือว่าไม่เป็นปริมาณเวกเตอร์ และถ้าครูออกคำสั่งใหม่ว่า “ให้นักเรียนทุกคนเดินไปทางทิศเหนือ” ซึ่งนักเรียนทุกคนก็จะเดินไปทางทิศเดียวกันคือทิศเหนือ ซึ่งในขณะที่เดินนั้นนักเรียนทุกคนก็จะสงสัยว่าให้เดินไปไกลเท่าไรเพราะคำสั่งของครูมีแต่ทิศทางแต่ไม่มีขนาด จึงไม่จัดว่าเป็นปริมาณเวกเตอร์ ดังนั้นเราจึงเห็นความสำคัญของขนาดและทิศทางว่าจะต้องบอกทั้ง 2 อย่างด้วยกันจึงจะเป็นเวกเตอร์ได้ เราสามารถพบปริมาณเวกเตอร์ได้ เช่น การกระจัด ความเร็ว ความเร่ง แรง น้ำหนักโมเมนตัม สนามแม่เหล็ก
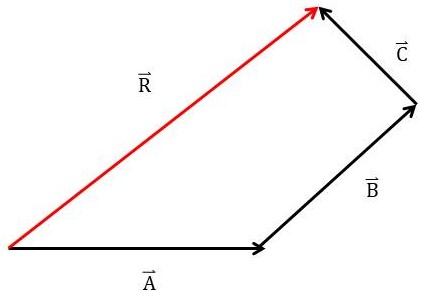
ภาพการหาเวกเตอร์ลัพธ์โดยการวาดรูป
ที่มา: กัญญา เกื้อกูล
สัญลักษณ์ของปริมาณเวกเตอร์
การแสดงขนาดและทิศทางของปริมาณเวกเตอร์จะใช้ลูกศรแทน โดยขนาดของปริมาณเวกเตอร์แทนด้วยความยาวของลูกศรตามอัตราส่วนที่เหมาะสม และทิศทางของปริมาณเวกเตอร์แทนด้วยทิศทางของหัวลูกศร
เวกเตอร์เท่ากัน หมายถึง เวกเตอร์ 2 เวกเตอร์เท่ากัน เมื่อเวกเตอร์ทั้งสองมีขนาดเท่ากันและมีทิศไปทางเดียวกัน
เวกเตอร์ตรงข้ามกัน หมายถึง เวกเตอร์ 2 เวกเตอร์ตรงข้ามกัน เมื่อเวกเตอร์ทั้งสองมีขนาดเท่ากัน แต่ทิศทางตรงข้ามกัน
การบวกลบเวกเตอร์
การบวก-ลบปริมาณเวกเตอร์ หรือการหาเวกเตอร์ลัพธ์ สามารถทำได้ 2 วิธีคือ
1) วิธีการเขียนรูป
2) วิธีคำนวณ
การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว
การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว มีขั้นตอนดังนี้
1) เขียนลูกศร แทนเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด
2) นำหางลูกศร แทนเวกเตอร์ที่ 2 ต่อกับหัวลูกศรของเวกเตอร์แรก
3) นำหางลูกศรแทนเวกเตอร์ที่ 3 ต่อกับหัวลูกศรของเวกเตอร์ที่ 2
4) ถ้ามีเวกเตอร์ย่อย ๆ อีก ให้นำเวกเตอร์อันต่อ ๆ ไป มากระทำดังข้อ 3 จนครบทุกเวกเตอร์
5) เวกเตอร์ลัพธ์ของเวกเตอร์ย่อย ๆ เหล่านั้นหาได้โดยการลากลูกศรจากหางของเวกเตอร์แรกไปยังหัวลูกศรของเวกเตอร์อันสุดท้าย ลูกศรที่ลากนี้แทนด้วยขนาดและทิศทางของเวกเตอร์ลัพธ์
การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบการสร้างรูปสี่เหลี่ยมด้านขนาน
การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบการสร้างรูปสี่เหลี่ยมด้านขนานมีขั้นตอนดังนี้
1) เมื่อทราบขนาดและทิศทางของแรงให้เขียนเส้นแสดงขนาดและทิศทางของแรงทั้งหมด แล้วเขียนลูกศร แทนเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด
2) นำหางลูกศร แทนเวกเตอร์ที่ 2 ต่อกับหางของลูกศรของเวกเตอร์แรก
3) ลากเส้นประต่อจากหัวลูกศรของแรงทั้งสอง ตามขนาดของและทิศทางของที่เส้นประขนาน เพื่อสร้างเป็นรูปสี่เหลี่ยม
4) ลากเส้นทแยงของรูปสี่เหลี่ยมจากหางลูกศรไปยังมุมตรงข้าม ซึ่งจะเป็นเวกเตอร์ลัพธ์ของแรงทั้งสอง โดยทิศทางของหัวลูกศรจะชี้ออกจากหางลูกศรของแรงทั้งสองไปยังมุมตรงข้าม
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ
เนื่องจากการหาเวกเตอร์ลัพธ์โดยวิธีการวาดรูปให้ผลลัพธ์ที่ไม่แม่นยำ เพียงแต่ได้คร่าว ๆ เท่านั้น เพราะถ้าลากความยาวหรือทิศทางลูกศรแทนเวกเตอร์คลาดเคลื่อนเพียงเล็กน้อยผลของเวกเตอร์ลัพธ์ก็จะคลาดเคลื่อนไปด้วยแต่หากการหาเวกเตอร์ลัพธ์โดยการคำนวณจะให้ผลลัพธ์ถูกต้องแน่นอน
เมื่อมีเวกเตอร์ย่อยเพียง 2 เวกเตอร์เท่านั้น
- ถ้าเวกเตอร์ทั้งสองไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของขนาดเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ทั้งสอง
- ถ้าเวกเตอร์ทั้งสองสวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของขนาดเวกเตอรลัพธ์ทั้งสองทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
- ถ้าเวกเตอร์สองเวกเตอร์ทำมุมตั้งฉากกัน เราสามารถคำนวณหาขนาดเวกเตอร์ลัพธ์ได้โดยการใช้สูตรของพีทาโกรัสมาช่วยในการคำนวณ และสามารถหาทิศทางของเวกเตอร์ได้โดยใช้หลักการวาดรูปสี่เหลี่ยมด้านขนาน
ดังนั้นจึงสรุปได้ว่า
เวกเตอร์ลัพธ์ของเวกเตอร์สองเวกเตอร์มีขนาดมากที่สุดเมื่อเวกเตอร์ทั้งสองมีทิศทางไปทางเดียวกัน และมีขนาดน้อยที่สุด เมื่อเวกเตอร์ทั้งสองมีทิศทางตรงข้ามกัน
ตัวอย่างที่ 1 เวกเตอร์ A ขนาด 5 หน่วย, เวกเตอร์ B ขนาด 4 หน่วย จงหาขนาดเวกเตอร์ลัพธ์ของเวกเตอร์ A และ เวกเตอร์ B ที่เป็นไปไม่ได้
- 1 หน่วย 2. 5 หน่วย 3. 8 หน่วย 4. 10 หน่วย
เฉลย คำตอบที่ถูกต้องคือ ข้อ 4 เวกเตอร์ 2 เวกเตอร์ รวมแล้วมากที่สุด เมื่อเวกเตอร์ทั้งสองไปทางเดียวกันเวกเตอร์ลัพธ์มีค่าเท่ากับผลบวกของเวกเตอร์ทั้งสอง (5+4 = 9) และเวกเตอร์ลัพธ์มีค่าน้อยสุดเมื่อเวกเตอร์ทั้งสองสวนทางกัน เวกเตอร์ลัพธ์มีค่าเท่ากับผลต่างของเวกเตอร์ทั้งสอง (5-4=1) ดังนั้นขนาดเวกเตอร์ลัพธ์ของเวกเตอร์ A และ เวกเตอร์ B มีค่าตั้งแต่ 1 ถึง 9 ซึ่งข้อ 4 ได้ระบุขนาดเวกเตอร์ลัพธ์ของเวกเตอร์ A และ เวกเตอร์ B เป็น 10 หน่วย ซึ่งเป็นไปไม่ได้ ดังนั้นข้อ 4 ถูก
ตัวอย่างที่ 2 เวกเตอร์ขนาด 3 หน่วย และ เวกเตอร์ขนาด 4 หน่วย ทำมุมตั้งฉากกัน จงหาเวกเตอร์ลัพธ์
วิธีทำ เมื่อเรารู้ขนาดและทิศทางของเวกเตอร์ทั้งสอง สามารถหาขนาดเวกเตอร์ลัพธ์ได้ดังนี้
R2 = A2 + B2
= 32 + 42
R2 = 25
R = 5 หน่วย
ดังนั้นเวกเตอร์ลัพธ์มีขนาด 5 หน่วย
แหล่งที่มา
กอบนวล จิตตินันทน์. (2537). วิทยาศาสตร์ ม.2. กรุงเทพฯ:ภูมิบัณฑิต
จรัญ บุระตะ. (2555). ฟิสิกส์ เล่ม 1 ม. 4-6. กรุงเทพฯ:นิพนธ์.
นิรันดร์ สุวรัตน์. (2554). คัมภีร์วิทยาศาสตร์ ฟิสิกส์ ม.ต้น. กรุงเทพฯ:พัฒนา.
กลับไปที่เนื้อหา
ในชีวิตประจำวันของเราต้องพบกับเหตุการณ์ต่าง ๆ ที่เกี่ยวข้องกับการใช้แรงชนิดต่าง ๆ อยู่เสมอไม่ว่าจะเป็นการเคลื่อนที่ของตัวเราเองหรือการเคลื่อนที่ของวัตถุต่าง ๆ ซึ่งการเคลื่อนที่ของตัวเรานั้นไม่ว่าจะเป็นการเดินการวิ่ง เราต้องออกแรงเพื่อให้ร่างกายของเราขยับและเคลื่อนไหว โดยใช้พลังงานจากกระบวน การเผาผลาญอาหาร และที่เท้าของเราต้องออกแรงกระทำต่อพื้นถนนซึ่งพื้นถนนก็จะออกแรงกระทำต่อเท้าเราเพื่อออกแรงกระทำต่อวัตถุเสมอซึ่งเมื่อเราออกแรงกระทำให้วัตถุมีการเคลื่อนที่โดยเราออกแรงกระทำต่อวัตถุอย่างสม่ำเสมอก็จะมีผลทำให้วัตถุมีการเปลี่ยนแปลงอัตราเร็วและความเร็วโดยถ้าเราออกแรงกระทำต่อวัตถุในทิศทางเดียวกันกับ การเคลื่อนที่ก็จะทำให้วัตถุเคลื่อนที่โดยมีความเร็วเพิ่มขึ้นและถ้าเราออกแรงกระทำต่อวัตถุที่กำลังเคลื่อนที่ในทิศทางตรงข้ามกับการเคลื่อนที่ก็จะทำให้วัตถุเคลื่อนที่โดยมีความเร็วลดลง นอกจากแรงมีผลทำให้วัตถุเกิดการเปลี่ยนแปลงการเคลื่อนที่แล้วแรงยังมีผลทำให้วัตถุเกิดการเปลี่ยนแปลงรูปร่างได้อีกด้วย เช่น เมื่อเราออกแรงกดที่ก้อนดินน้ำมันก็จะมีผลทำให้ก้อนดินน้ำมันเปลี่ยนแปลงรูปร่างไป ดังนั้นแรงที่กระทำต่อวัตถุสามารถทำให้วัตถุเกิดการเปลี่ยนแปลงอย่างมากมาย เช่ย ทำให้วัตถุที่อยู่นิ่งเกิดการการขยับและเคลื่อนที่ หรือทำให้วัตถุที่กำลังเคลื่อนที่หยุดนิ่งได้และทำให้วัตถุมีการเปลี่ยนรูปร่างไป และนอกจากนี้ยังพบอีกว่าถ้ามีแรงลัพธ์ของแรงสองแรงกระทำต่อวัตถุหนึ่งโดยแรงทั้งสองกระทำต่อวัตถุในทิศทางเดียวกันแรงลัพธ์ที่ได้จะเท่ากับผลรวมของแรงทั้งสอง แต่ถ้าแรงทั้งสองกระทำต่อวัตถุในทิศทางตรงข้ามกัน แรงลัพธ์ที่ได้ก็จะมีค่าเท่ากับผลต่างของแรงทั้งสองนั้น
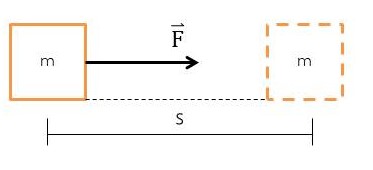
ภาพการออกแรงกระทำต่อวัตถุมวล m เคลื่อนที่ด้วยระยะ s
ที่มา: กัญญา เกื้อกูล
แรง (force) เป็นผลมาจากการใช้พลังงานที่กระทำต่อวัตถุมีผลทำให้วัตถุเกิดการเปลี่ยนแปลงรูปร่างหรือวัตถุเกิดการเปลี่ยนแปลงการเคลื่อนที่ เช่น การออกแรงยกหรือแบกวัตถุ การออกแรงผลักกล่อง การออกแรงกระทำกับตะปูในขณะที่ใช้ค้อนตอกตะปูหรือการที่คนยืนนิ่งอยู่กับที่และวัตถุวางอยู่นิ่ง ๆ ก็ยังพบว่ามีแรงกระทำต่อคนที่ยืนนิ่งอยู่กับที่และวัตถุที่วางอยู่นิ่ง ๆ
ถ้าพิจารณาแรงที่กระทำต่อกล่องใบหนึ่ง โดยคนออกแรงผลักกล่องไปทางขวามือ จะพบว่า มีแรงที่กระทำต่อกล่องดังนี้ แรงที่คนออกแรงผลักกระทำต่อกล่อง และมีแรงโน้มถ่วงของโลกกระทำต่อกล่องในทิศลง ซึ่งก็คือน้ำหนักของกล่องนั่นเอง และที่ผิวสัมผัสระหว่างกล่องกับพื้นก็ยังมีแรงที่พื้นดันกล่องขึ้นในแนวดิ่ง และถ้าพิจารณากรณีคนหรือวัตถุที่วางอยู่นิ่ง ๆ ก็จะมีแรงโน้มถ่วงของโลกกระทำต่อคนหรือวัตถุในทิศลงซึ่งก็คือน้ำหนักของคนและวัตถุ และที่เท่าของคนก็จะมีแรงที่พื้นดันเท้าขึ้นในแนวดิ่งนั่นเอง จากการที่มีแรงกระทำต่อวัตถุในลักษณะต่าง ๆ นั้นทำให้เราสนใจที่จะศึกษาว่าแรงที่กระทำต่อวัตถุนั้นมีขนาดเท่าใดและมีทิศทางอย่างไร
ขนาดและทิศทางของแรง
เมื่อเราออกแรงกระทำต่อวัตถุและทำให้วัตถุเกิดการเคลื่อนที่ การหาขนาดของแรงที่กระทำต่อวัตถุหรือน้ำหนักของวัตถุนั้น เราสามารถทำได้โดยใช้เครื่องชั่งสปริงวัด ซึ่งจากการใช้เครื่องชั่งสปริงชั่งน้ำหนักของวัตถุในแนวดิ่ง ค่าที่อ่านได้จากเครื่องชั่งสปริง คือน้ำหนักของวัตถุนั้น ส่วนการใช้เครื่องชั่งสปริงลากหรือดึงวัตถุให้เคลื่อนที่ไปตามแนวราบ ค่าที่อ่านได้จากเครื่องชั่งสปริง คือ ขนาดของแรงที่กระทำต่อวัตถุนั้น ถ้าเราใช้เครื่องชั่งสปริงดึงวัตถุให้เคลื่อนที่จะพบว่า วัตถุเคลื่อนที่ไปตามทิศทางเดียวกับแรงดึงและเมื่อเพิ่มจำนวนของวัตถุให้มากขึ้นพบว่าแรงที่อ่านได้จากเครื่องชั่งสปริงก็มีค่าเพิ่มขึ้น สรุปได้ว่าแรงที่กระทำต่อวัตถุเป็นปริมาณเวกเตอร์ เพราะเป็นปริมาณที่มีทั้งขนาดและทิศทางแรงเป็นปริมาณเวกเตอร์ ดังนั้นเมื่อมีแรงที่อยู่ในแนวเดียวกันมากระทำต่อวัตถุเดียวกันหลาย ๆ แรงเราสามารถรวมแรงที่กระทำต่อวัตถุนั้นได้ เมื่อมีแรงตั้งแต่สองแรงขึ้นไปมากระทำต่อวัตถุก้อนเดียวกัน เปรียบเสมือนว่ามีแรงเพียงเดียวเท่านั้นที่กระทำต่อวัตถุ เรียกว่าแรงลัพธ์ และวัตถุจะเคลื่อนที่ไปตามทิศทางของแรงลัพธ์เสมอ
การรวมแรงตั้งแต่สองแรงที่กระทำต่อวัตถุ หรือ การหาแรงลัพธ์
- แรงที่กระทำต่อวัตถุมีทิศทางเดียวกันและขนานกัน เราสามารถหาแรงลัพธ์ได้โดยนำขนาดของแรงทั้งสองมารวมกัน และทิศทางของแรงลัพธ์มีทิศทางตามแนวแรง
- แรงที่กระทำต่อวัตถุมีทิศทางตรงข้ามกันและขนานกัน สามารถหาขนาดของแรงได้โดยการนำขนาดของแรงทั้งสองมาหักล้างกัน และทิศทางของแรงลัพธ์มีทิศทางตามแนวแรงที่มีขนาดมากกว่า
- ถ้าแรงสองแรงทำมุมตั้งฉากกันสามารถคำนวณหาได้โดยใช้สูตรของพีทาโกรัส และทิศทางของแรงสามารถหาได้โดยการสร้างรูปสี่เหลี่ยมด้านขนานหรือใช้สูตรคำนวณดังต่อไปนี้
หาขนาด
R2 = (F1)2 + (F2)2
หาทิศทาง
tan = sin θ /cos θ
- ถ้าแรงสองแรงทำมุมใด ๆ ต่อกัน สามารถหาแรงลัพธ์ได้ใช้สูตรคำนวณหาขนาดของแรงลัพธ์ โดยใช้สมการต่อไปนี้
หาขนาด
R2 = (F1)2 + (F2)2 + (2)(F1)(F2) cos θ
หาทิศทาง
tan = F2 sins θ /(F1 + F2sins θ)
แหล่งที่มา
กอบนวล จิตตินันทน์. (2537). วิทยาศาสตร์ ม.2.กรุงเทพฯ:ภูมิบัณฑิต
จรัญ บุระตะ. (2555). ฟิสิกส์ เล่ม 1 ม. 4-6. กรุงเทพฯ:นิพนธ์.
นิรันดร์ สุวรัตน์. (2554). คัมภีร์วิทยาศาสตร์ ฟิสิกส์ ม.ต้น. กรุงเทพฯ:พัฒนา.
กลับไปที่เนื้อหา



