การเคลื่อนที่ในหนึ่งและสองมิติ

ในชีวิตประจำวัน เราจะเห็นการเคลื่อนที่ของสิ่งต่าง ๆ มากมาย หลากหลายรูปแบบ เช่นการเคลื่อนที่ของอวัยวะต่าง ๆ ของคนเดิน นกบิน รถยนต์แล่น และใบไม้ร่วง เป็นต้น เมื่อ พิจารณาการเคลื่อนที่เหล่านั้นแล้ว จะพบว่า ส่วนใหญ่มีลักษณะซับซ้อน เช่น มีเส้นทางการ เคลื่อนที่เป็นแนวเส้นโค้งวกวน เพื่อให้ง่ายต่อการเข้าใจการเคลื่อนที่เราจะเริ่มศึกษาจากการ เคลื่อนที่เฉพาะในแนวเส้นตรงก่อน แล้วจึงจะขยายความเข้าใจ กับการเคลื่อนที่ในสองและสามมิติ หรือในลักษณะที่ซับซ้อนในลำดับต่อไป

ตำแหน่งและการกระจัด

ตำแหน่ง (position) คือการแสดงออก หรือการบอกให้ทราบว่า วัตถุหรือสิ่งของ ที่เราพิจารณา อยู่ที่ใด เราจะคิดถึงวัตถุที่มีขนาดเล็กก่อน ซึ่งจะสามารถบอกได้ชัดเจนว่ามี ตำแหน่งอยู่ที่ใด โดยเฉพาะ บนเส้นตรงเส้นหนึ่งเมื่อเทียบกับจุดอ้างอิง จุดอ้างอิงเป็นปัจจัย จำเป็นเพื่อความชัดเจน อาจจะเป็นจุด ศูนย์ของโคออร์ดิเนตในพิกัด xy เนื่องจากเราจะ พิจารณากรณีหนึ่งมิติก่อน เราจะใช้เฉพาะแกน x และอาจบอกว่าวัตถุของเราอยู่ที่

ความเร็วเฉลี่ยและอัตราเร็วเฉลี่ย

โดยนิยามหรือข้อกำหนด ความเร็ว (Velocity) คือ การเปลี่ยนตำแหน่งต่อเวลา สำหรับ
ช่วงเวลาที่ยาว ความเร็วที่คิดจากการเปลี่ยนตำแหน่งในช่วงเวลานั้นหารด้วยช่วงเวลาถือว่า
เป็นความเร็วเฉลี่ย (Average Velocity)ความเร็วเฉลี่ยเป็นเสมือนความเร็วที่การเปลี่ยนแปลง ในช่วงเวลาที่วัดมี

โดยเครื่องหมายขีดสองข้างของปริมาณจะหมายถึง ขนาดของปริมาณนั้นและมีค่าเป็นบวกเท่านั้นสมมติว่า โยนลูกบอลขึ้นในแนวดิ่ง ลูกบอลลอยขึ้นไปได้สูง 5 เมตร แล้วตกกลับมายังมือในเวลา 2 วินาที จากข้อความนี้แสดงว่า อัตราเร็วเฉลี่ยในช่วง 2 วินาทีเท่ากับระยะทาง 5 เมตร + 5 เมตร หารด้วยเวลา 2 วินาที เท่ากับ 5 เมตรต่อวินาทีแต่ความเร็วเฉลี่ย ในช่วงเดียวกันจะเป็นศูนย์เพราะ ลูกบอลได้กลับมาที่เดิมคือ มีการกระจัดทั้งหมดเป็นศูนย์

ความเร็วและอัตราเร็วขณะใดขณะหนึ่ง

ความเร็วขณะใดขณะหนึ่ง (Instantaneous velocity) ก็คือความเร็วของวัตถุในช่วงเวลาที่ สั้นมากขณะผ่านจุดจุดหนึ่งหรือที่เวลาใดเวลาหนึ่ง หรือพูดสั้น ๆ เป็น
ความเร็วในช่วงเวลาที่สั้นมาก นั้นคือ

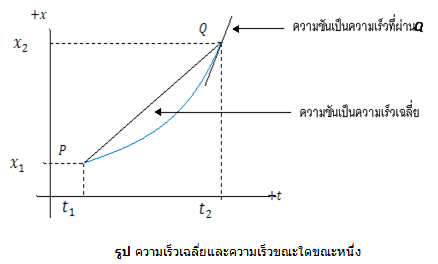
ตารางแสดงค่า X ของ P และ Q ที่เวลาต่าง ๆ และค่าความชันของเส้น PQ

ตารางแสดงว่าความชันไม่เปลี่ยนเมื่อtเข้าใกล้ 2.00 วินาทีมาก

เมื่อช่วงเวลาสั้นมากวัตถุไม่มีเวลาที่จะกลับไปมาอัตราเร็วที่ขณะใดขณะหนึ่งก็คือขนาด

ของความเร็วที่ไม่ต้องคำนึงถึงทิศทางนั่นเอง

ความเร่ง

หากเขียนกราฟของความเร็วกับเวลา ความชันของเส้นสัมผัสที่จุดต่าง ๆ ก็คือความเร่งของ วัตถุที่จุดนั้นๆ ในทำนองเดียวกันกับที่ความเร็วเป็นความชันของ กราฟระหว่างตำแหน่งกับเวลา สำหรับคำว่า อัตราเร่งก็จะไม่คิดทิศทางในลักษณะ เดียวกับอัตราเร็ว

การเคลื่อนที่ในกรณีความเร่งเป็นค่าคงตัว

 กรณีที่ความเร่งมีค่าคงตัว (Constant acceleration) นั่นคือ ความเร็วมีการเปลี่ยนแปลง

แบบสม่ำเสมอ กราฟของความเร็วที่เพิ่มขึ้นอย่างสม่ำเสมออาจเป็นดังรูป ซึ่งกราฟความเร็วกับ เวลาเป็นกราฟเส้นตรง ความชันที่ทุกจุดบนเส้นตรงคือ ความชันของเส้นตรงนั่นเอง

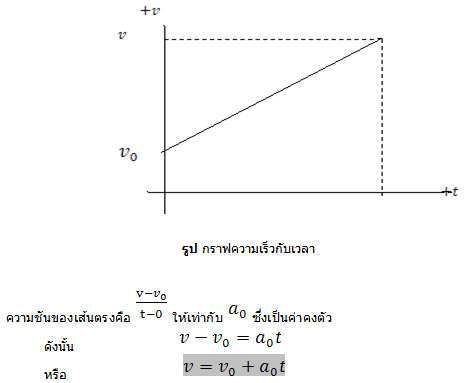
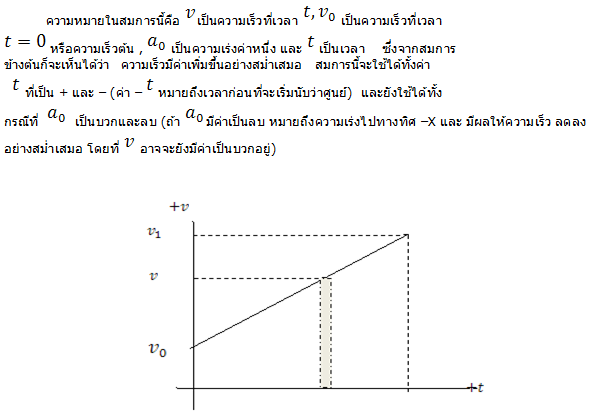
รูปกราฟระหว่างความเร็วและเวลา สำหรับความเร่งคงตัว

ดังนั้นสูตรจะเป็นดังนี้

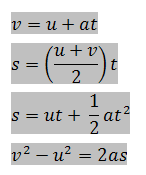
สูตรเหล่านี้ใช้ได้เฉพาะกรณีที่aเป็นค่าคงตัวเท่านั้น 

วัตถุตกอย่างเสรีมีความเร่งสม่ำเสมอ

สามารถทดลองด้วยตัวเองว่า สิ่งของหรือวัตถุต่าง ๆ ไม่ว่าจะมีมวลเท่าใด (ซึ่งถ้าความหนาแน่นมากพอแรงต้านของอากาศจะไม่มีผลกระทบมากนัก) จะตกลง สู่พื้นด้วยความเร่งสม่ำเสมอ นั่นคือ ความเร่งมีค่าคงตัวและมีทิศลงในแนวดิ่งเสมอ เรียกได้ว่าค่า ความเร่งของการตกอย่างเสรี การตกอย่างเสรี (free fall) หมายถึง การตกโดย ไม่มีสิ่งใดกีดขวางหรือกระทบ การมีอากาศกระทบระหว่างตกทำให้ไม่ได้ผลดังอุดมคติ แต่อาจพิสูจน์ได้ว่าการมีอากาศไม่ทำให้การตกผิดไปจากอุดมคติมากนักโดยเฉพาะเมื่อ

ความเร็วไม่มาก แต่ถ้าวัตถุตกจากที่สูง วัตถุมีความเร็วมากในช่วงท้ายซึ่งอากาศจะต้าน ทานการเคลื่อนที่มากขึ้น และทำให้ความเร่งผิดไป ความเร่งในการตกของวัตถุลงสู่พื้น

โลกเรียกว่า ค่าโน้มถ่วง (gravity) และใช้สัญลักษณ์เป็น g ค่าของความเร่งในจุดต่าง ๆ ของประเทศไทย จะมีค่าระหว่าง 9.780 ถึง 9.785 เมตรต่อวินาทีกำลังสอง ค่านี้ขึ้นกับ ละติจูดของจุดที่ทดลอง ค่าเฉลี่ยของ g ทั่วโลกที่ถือเป็นค่ามาตรฐานคือ 9.8065 เมตรต่อวินาทีกำลังสอง

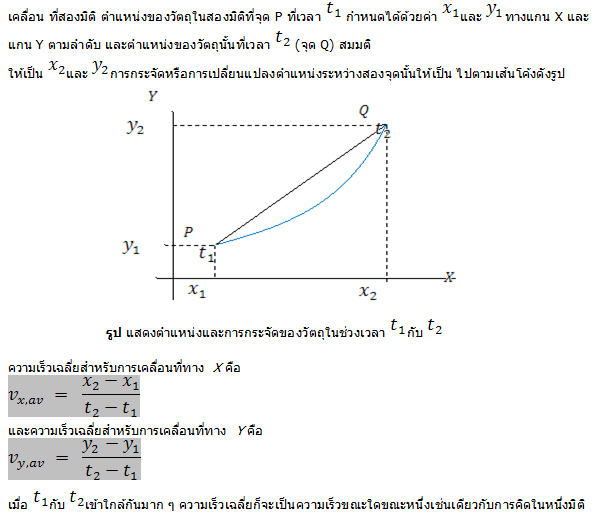
การเคลื่อนที่ในสองมิติ และสามมิติ

การเคลื่อนที่ในสองมิติสามารถแยกคิดแบบการเคลื่อนที่หนึ่งมิติที่ตั้งฉากกัน และสามารถ นำการคิดสองทางนั้นมาประกอบกันหรือนำมารวมกันแบบเวกเตอร์ได้ ตามแนวของแกนสามแกนที่ ตั้งฉากซึ่งกัน คือ ตามแกนของระบบโคออร์ดิเนต XYZ สำหรับการเคลื่อนที่สามมิติ และตามแกน ของระบบโคออร์ดิเนต XY สำหรับการ

ความเร็วสัมพัทธ์ (Relative Velocity)

การจะบอกว่าวัตถุอยู่ที่ตำแหน่งใดให้ชัดเจน และเป็นที่เข้าใจกันได้เป็นอย่างดี ย่อมต้องมีจุดอ้างอิงและแกนอ้างอิง นั่นคือ มีระบบโคออร์ดิเนตอ้างอิง ถ้ามีผู้สังเกตสองคน ต่างใช้ระบบโคออร์ดิเนตของตนเองและเคลื่อนที่สัมพัทธ์กัน นั่นคือ ระบบหนึ่งมีความเร็ว เมื่อเทียบกับอีกระบบหนึ่ง สิ่งนี้เป็นไปได้เสมอ เมื่อเป็นเช่นนี้ วัตถุที่เห็นอยู่นิ่งในระบบหนึ่ง ก็จะปรากฎในอีกระบบหนึ่ง ตัวอย่างเช่น ขณะที่รถไฟวิ่งด้วยความเร็วคงตัวผ่านชานชาลา แห่งหนึ่งผู้โดยสารในรถไฟทำของหล่นจากมือลงพื้น ผู้สังเกตในรถไฟเห็นวัตถุนั้นตกลง ด้วยความเร่งในแนวดิ่ง ทั้งนี้เทียบกับตัวเองในรถไฟ ส่วนผู้ที่อยู่บนชานชาลานอกรถไฟ มองผ่านหน้าต่างเห็นว่าวัตถุตกลงเป็นวิถีโค้งแบบโพรเจกไทล์ตัวอย่างของการสังเกตที่เกี่ยวกับความเร็วสัมพัทธ์ เช่น ขณะที่ฝนตก ให้เม็ดฝนมีขนาดที่ทำให้ตกด้วยความเร็วสม่ำเสมอ 10 เมตรต่อวินาที และตกลงในแนวดิ่งในอากาศนิ่ง (สำหรับผุ้สังเกตอยู่นิ่ง) สำหรับผู้สังเกตที่อยู่ในรถยนต์วิ่งด้วยความเร็ว 36 กิโลเมตรต่อชั่วโมง (10 เมตรต่อวินาที) จะเห็นเม็ดฝนตกอย่างไร ซึ่งความเร็วของเม็ดฝนที่เห็นจะเป็นความเร็วสัมพัทธ์กับผู้สังเกตที่เคลื่อนที่นั่นเอง สิ่งที่ลอยอยู่นิ่งในอากาศข้างหน้าของผู้สังเกตที่ออยู่ในรถ ผู้สังเกตย่อมเห็น สิ่งนั้นเคลื่อนที่เข้าหาด้วยความเร็วมีขนาดเท่าที่รถวิ่ง ซึ่งหมายถึงความเร็วในทิศตรงกันข้าม กับการเคลื่อนที่ของตนเอง สิ่งที่อยู่นิ่งด้านข้าง หรือหลังของผู้สังเกตก็จะปรากฎมีความเร็วเช่นเดียวกัน เพราะฉะนั้นผู้สังเกตจึงจะเห็นเม็ดฝนมีความเร็วเดิม บวกด้วยความเร็วมีทิศตรงกันข้ามกับความเร็ว