การเคลื่อนที่แบบต่าง ๆ (โพรเจกไทล์,วงกลม,ทางโค้ง)
การเคลื่อนที่แบบโพรเจกไทล์ หมายถึง การเคลื่อนที่ของวัตถุที่ประกอบด้วยการเคลื่อนที่ 2 แนวตั้งฉากกัน และเกิดขึ้นในเวลาเดียวกัน เช่น การขี่จักรยานผาดโผน เป็นเส้นทางโค้งจากเนินด้านหนึ่งไปยังเนินอีกด้านหนึ่ง การเคลื่อนที่ของวัตถุที่ถูกขว้างขึ้นไปในอากาศในแนวที่ทำมุม θ ใด ๆ กับแนวราบด้วยอัตราเร็ว u เราสามารถวิเคราะห์ความเร็วการเคลื่อนที่ของวัตถุออกมาได้ดังภาพ

ภาพที่ 1 ขว้างวัตถุแนววิถีโค้ง
ที่มา : https://pixabay.com/th ; domeckopol
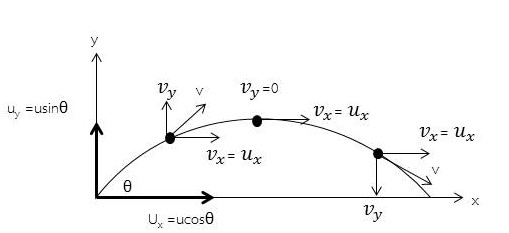
ภาพที่ 2 แสดงแนวการเคลื่อนที่และความเร็วที่ตำแหน่งใด ๆ
ที่มา : กัญญา เกื้อกูล
ความเร็วต้นในแนวราบ = ucos θ
และ ความเร็วต้นในแนวดิ่ง = usin θ
การที่วัตถุมีความเร็วต้นถึงสองแนวเช่นนี้ ทำให้วัตถุมีการเคลื่อนที่ในแนวทั้งสองพร้อมกัน คือ การเคลื่อนที่ในแนวราบและการเคลื่อนที่ในแนวดิ่ง เมื่อรวมการเคลื่อนที่ทั้งสองนี้เข้าด้วยกัน แนวการเคลื่อนที่ของวัตถุที่ปรากฏจะเป็นวิถีโค้งในอากาศ
เนื่องจากการเคลื่อนที่แบบโพรเจกไทล์ประกอบไปด้วยการเคลื่อนที่ใน 2 แนว ทำให้แบ่งการคำนวณเกี่ยวกับการเคลื่อนที่แบบโพรเจกไทล์ออกได้เป็น 2 ส่วนคือ การคำนวณในแนวราบและการคำนวณในแนวดิ่ง
การวิเคราะห์การเคลื่อนที่แบบโพรเจกไทล์ในแนวราบ
โดยทั่วไป การคำนวณกรณีของการขว้างวัตถุขึ้นไปในอากาศด้วยความเร็วต้น u และทำมุม θ ใด ๆ กับแนวราบเราจะพิจารณาโดยถือว่าไม่มีแรงมากระทำต่อวัตถุในแนวราบ เราจึงพิจารณาการเคลื่อนที่นี้เช่นเดียวกับการเคลื่อนที่ของวัตถุด้วยความเร็วคงที่ และใช้สมการคำนวณเป็นดังนี้
ระยะทาง = อัตราเร็ว × เวลา
การวิเคราะห์การเคลื่อนที่แบบโพรเจกไทล์ในแนวดิ่ง
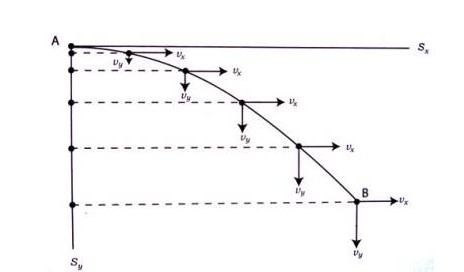
ภาพที่ 3 การเปรียบเทียบระยะทางในแนวดิ่งระหว่างวัตถุที่มีการเคลื่อนที่แบบโพรเจกไทล์และการเคลื่อนที่ในแนวดิ่งอย่างเสรีของวัตถุ
ที่มา : กัญญา เกื้อกูล
จากภาพที่ 3 แสดงการการเปรียบเทียบระยะทางในแนวดิ่งของวัตถุที่มีการเคลื่อนที่ในแนวดิ่งอย่างเสรีด้วยความเร็วต้นเท่ากับศูนย์ กับวัตถุที่มีการเคลื่อนที่แบบโพรเจกไทล์ที่มีความเร็วต้นอยู่ในแนวระดับ อันมีผลทำให้ความเร็วต้นในแนวดิ่งของวัตถุมีค่าเป็นศูนย์เช่นกัน โดยวัตถุทั้ง 2 ในภาพเริ่มต้นเคลื่อนที่พร้อมกันจากภาพแสดงให้เห็นว่า เมื่อเวลาผ่านไป ระยะทางในแนวดิ่งของวัตถุทั้งสองเท่ากันทุกขณะ ทั้งนี้ทั้งการเคลื่อนที่ในแนวดิ่งอย่างเสรีและการเคลื่อนแบบโพรเจกไทล์ ต่างก็เป็นการเคลื่อนที่ภายใต้แรงความโน้มถ่วงของโลก
ดังนั้นจึงสรุปได้ว่า การคำนวณในส่วนแนวดิ่งของวัตถุที่เคลื่อนที่แบบโพรเจกไทล์ทำได้ โดยใช้วิธีการคำนวณของการเคลื่อนที่ในแนวดิ่งอย่างเสรี นั่นคือ
1) ต้องกำหนดเครื่องหมายของปริมาณเวกเตอร์ทุกชนิด
2) ความเร่งของวัตถุมีค่าเท่ากับ g ซึ่งมีทิศลงเสมอ
จากที่กล่าวมาจะเห็นได้ว่า การคำนวณในแนวราบและแนวดิ่งต่างก็เป็นอิสระซึ่งกันและกันซึ่งถ้าทราบความเร่งในแต่ละแนวแล้วก็สามารถหาปริมาณต่าง ๆ ในแนวนั้นได้จากสมการของการเคลื่อนที่ในแนวตรง ได้แก่
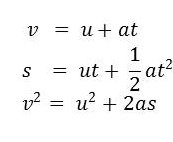
การคำนวณหาระยะทางในแนวราบ
จากการพิจารณาการเคลื่อนที่แบบโพรเจกไทล์ที่มีความเร็วต้น u ทำมุม θ กับแนวราบ การเคลื่อนที่นี้มีอัตราเร็วต้นในแนวราบและแนวดิ่งเป็น ucosθ และ usinθ ตามลำดับ
สำหรับการเคลื่อนที่ในแนวดิ่ง เมื่อกำหนดให้ปริมาณเวกเตอร์ที่มีทิศลงเป็นบวก ก็จะคำนวณหาเวลาของการเคลื่อนที่ได้จากสมการ
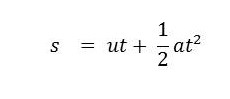
แทนค่าโดยให้ sy เป็นระยะทางในแนวดิ่ง จะได้
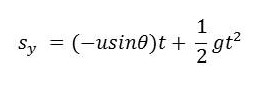
ถ้าการเคลื่อนที่เกิดจากการขว้างวัตถุจากพื้นราบ และวัตถุตกลงมายังพื้นราบเดิม ก็จะได้ระยะทางในแนวดิ่ง หรือ sy เป็นศูนย์
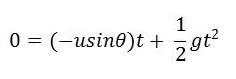
จะทำให้ได้เวลาที่ใช้ในการเคลื่อนที่เป็น
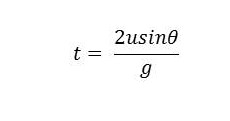
สำหรับการเคลื่อนที่ในแนวราบ หากถือว่าไม่มีแรงภายนอกในแนวราบมากระทำ และให้ sx เป็นระยะทางของการเคลื่อนที่ในแนวราบนี้ จะได้
sx = (ucosθ ) t
จัดรูปสมการใหม่ จะได้
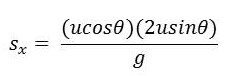
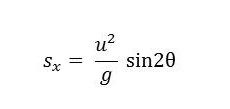
จากสมการข้างต้นจะเห็นว่า สำหรับอัตราเร็วต้นค่าหนึ่ง ๆ ระยะทางในแนวราบของวัตถุมีค่าขึ้นกับ sin2θ โดยค่าสูงสุดของระยะทางในแนวราบคือ u2/g ซึ่งเกิดขึ้นเมื่อ
sin2 θ = 1
= sin90o
หรือ 2θ = 90o
θ = 45o
นั่นคือ สำหรับอัตราเร็วต้นค่าหนึ่ง ๆ ถ้าทิศทางของความเร็วต้นทำมุม 45o กับแนวราบจะได้การเคลื่อนที่แบบโพรเจกไทล์ที่มีระยะทางในแนวราบมากที่สุด ในทางกลับกัน ถ้าต้องการขว้างวัตถุให้เคลื่อนที่แบบโพรเจกไทล์ และให้ระยะทางในแนวราบของวัตถุมีค่าหนึ่ง ความเร็วต้นที่น้อยที่สุดที่ใช้ในการขว้างวัตถุจะเกิดขึ้นเมื่อทิศทางของความเร็วต้นทำมุม 45o กับแนวราบ
ดังนั้นจึงสรุปเกี่ยวกับการเคลื่อนที่แบบโพรเจกไทล์ได้ว่า
1) แนวระดับ ความเร็วคงตัว ความเร่งเท่ากับศูนย์
2) แนวดิ่ง ความเร็วไม่คงตัว ความเร่งคงตัวเท่ากับ g
3) แนวโค้งโพรเจกไทล์ ความเร็วไม่คงตัว (คิดแนวระดับ + แนวดิ่ง)
4) ทั้งแนวระดับ และแนวดิ่ง ใช้เวลาในการเคลื่อนที่เท่ากัน
5) ที่จุดสูงสุด อัตราเร็วหรือความเร็ว จะเท่ากับอัตราเร็ว หรือความเร็วของแนวระดับ เพราะของแนวดิ่งเท่ากับศูนย์
6) เมื่อกล่าวถึงอัตราเร็วหรือความเร็วจะหมายถึงอัตราเร็ว หรือความเร็วในแนวโค้งโพรเจกไทล์ ซึ่งเป็นผลจากการคิดรวมแนวระดับแนวดิ่งเข้าด้วยกัน
7) วัตถุเคลื่อนที่แบบโพรเจกไทล์ มีแรงดึงดูดของโลกเพียงแรงเดียวเท่านั้นที่กระทำกับวัตถุ
จากสมการ
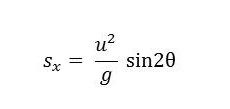
8) ถ้า u คงที่ ค่า sx จะมากที่สุดเมื่อ sin2θ มีค่ามากที่สุดนั่นคือ sin2θ = 1
9) ถ้า sx คงที่ ค่า u จะน้อยที่สุดเมื่อ θ = 45o ด้วยเช่นกัน
10) ถ้า u คงที่ ค่า sx จะเท่ากันสำหรับทกมุม θ คู่ใด ๆ ที่บวกกันได้ = 90o เช่น 30o กับ 60o ได้ sin 30ocos 30o = sin 60ocos 60o, 37o กับ 53o ได้ sin 37ocos 37o = sin 53ocos 53o
แหล่งที่มา
ณสรรค์ ผลโภค. (2559). ฟิสิกส์ เล่ม 1 กลศาสตร์. กรุงเทพ: Science center.
พงษ์ศักดิ์ ชินนาบุญ. (2554). ฟิสิกส์ เล่ม 1 ชั้นมัธยมศึกษาปีที่ 4-6 กรุงเทพ:วิทยพัฒน์.
กลับไปที่เนื้อหา
การเคลื่อนที่แบบวงกลม
การเคลื่อนที่แบบวงกลม เป็นการเคลื่อนที่ใน 2 มิติอีกแบบหนึ่ง ที่ทิศทางของแรงกระทำหรือความเร่งของวัตถุจะมีทิศที่เปลี่ยนไปตลอดเวลาที่วัตถุเคลื่อนที่ โดยจะมีทิศตั้งฉากกับแนวการเคลื่อนที่ของวัตถุตลอดเวลา คือจะมีทิศอยู่ในแนวรัศมีของวงกลมที่วัตถุเคลื่อนที่

ภาพที่ 1 การเคลื่อนที่แบบวงกลม
ที่มา: https://www.bbc.com/news/uk-england-stoke-staffordshire-32972169
การเคลื่อนที่แบบวงกลมในแนวระดับ
การเคลื่อนที่ของวัตถุแบบวงกลมในแนวระดับ เช่น แกว่งวัตถุที่ผูกติดปลายเชือกให้เคลื่อนที่เป็นวงกลมในแนวระดับ ลักษณะของการเคลื่อนที่เป็นดังภาพ
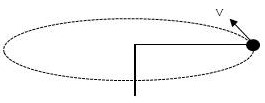
ภาพที่ 2 การเคลื่อนที่แบบวงกลมของวัตถุ
ที่มา: กัญญา เกื้อกูล
วัตถุที่เคลื่อนที่เป็นวงกลมด้วยอัตราเร็ว v คงตัว จะมีแรงลัพธ์มากระทำกับวัตถุในทิศพุ่งเข้าสู่ศูนย์กลาง และตั้งฉากกับทิศของความเร็วในแนวเส้นสัมผัสวงกลมซึ่งเปลี่ยนแปลงตลอดเวลา ทำให้เกิดความเร่งในทิศทางเดียวกับแรงลัพธ์ แรงลัพธ์นี้จะทำหน้าที่เป็นแรงสู่ศูนย์กลาง Fc มีขนาดเท่ากับ มวล m คูณความเร่งสู่ศูนย์กลาง ac
ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แบบวงกลม
คาบ (T) หมายถึง เวลาที่ใช้ในการเคลื่อนที่ครบ 1 รอบ มีหน่วยเป็น วินาที (s)
ความถี่ (f) หมายถึง จำนวนรอบที่เคลื่อนที่ได้ในเวลา 1 วินาที่ มีหน่วยเป็น ต่อวินาที (s-1) หรือ เฮิรตซ์ (Hz)
อัตราเร็วเชิงมุม (ω) หมายถึง อัตราส่วนของมุมที่วัตถุเคลื่อนที่เบี่ยงเบนไปจากแนวเดิม (เท่ากับมุมที่รัศมีวงกลมกวาดไป) ต่อเวลาที่ใช้ในการเคลื่อนที่ มีหน่วยเป็น เรเดียนต่อวินาที (rad/s)
อัตราเร็วเชิงเส้น (v) หมายถึง ระยะทางที่วัตถุเคลื่อนที่ได้ 1 รอบ ต่อเวลา 1 รอบ มีหน่วยเป็น เมตรต่อวินาที (m/s)
ตัวอย่างที่ 1 ข้อใดกล่าวถูกต้อง และข้อใดกล่าวผิด เกี่ยวกับการแกว่งวัตถุให้เคลื่อนที่แบบวงกลมในแนวระดับด้วยอัตราเร็วคงตัว
1.1 เป็นการเคลื่อนที่ที่มีความเร็วคงตัว
ตอบ ผิด เพราะมีขนาดของความเร็วหรืออัตราเร็วคงตัว ความเร็วไม่คงตัวทิศการเคลื่อนที่เปลี่ยนตลอด
1.2 เป็นการเคลื่อนที่แบบไม่มีความเร่ง
ตอบ ผิด เพราะ มีความเร่งเนื่องจากความเร็วไม่คงตัว
1.3 แรงลัพธ์ที่กระทำกับวัตถุเป็นศูนย์
ตอบ ผิด เพราะ แรงลัพธ์ไม่เป็นศูนย์ เพราะมีความเร่ง
1.4 ความเร่งมีทิศทางเดียวกันกับความเร็ว
ตอบ ผิด เพราะ ความเร่งมีทิศทางเดียวกันกับความเร็วที่เปลี่ยนไป และตั้งฉากกับทิศของความเร็วขณะนั้น ๆ ซึ่งอยู่ในแนวเส้นสัมผัสส่วนโค้ง
1.5 อัตราเร็วเฉลี่ยเท่ากับอัตราเร็วขณะใดขณะหนึ่ง
ตอบ ถูกต้อง อัตราเร็วคงตัว อัตราเร็วเฉลี่ยจะเท่ากับอัตราเร็วขณะใดขณะหนึ่ง
1.6 มวลของวัตถุไม่มีผลต่อขนาดความเร่ง
ตอบ ผิด เพราะ มวลของวัตถุมีผลต่อขนาดความเร่ง ac=Fc/m
1.7 แรงสู่ศูนย์กลางคงตัว และไม่เท่ากับศูนย์
ตอบ ผิด เพราะ ขนาดแรงสู่ศูนย์กลางคงตัว และไม่เท่ากับศูนย์ แต่แรงสู่ศูนย์กลางไม่คงตัว เพราะทิศทางเปลี่ยนไปตามแนวรัศมีของวงกลมในขณะเคลื่อนที่
1.8 เมื่อรู้ คาบ สามารถหาความถี่ และอัตราเร็วเชิงมุมได้
ตอบ ถูกต้อง เพราะ เมื่อรู้ คาบ (T) สามารถหา ความถี่ f =1/T และ อัตราเร็วเชิงมุม ω = 2π/T ได้
1.9 วัตถุที่เคลื่อนที่ด้วยความถี่สูง ขนาดแรงสู่ศูนย์กลางจะมากด้วย
ตอบ ถูกต้อง เพราะ เมื่อ ความถี่ (f) สูงขึ้นค่าของความเร็ว (v) จะมากขึ้นตาม v= 2πf ทำให้ Fc มากขึ้นด้วย Fc = mv2/r
การเคลื่อนที่แบบวงกมในระนาบดิ่ง
การเคลื่อนที่ของวัตถุแบบวงกลมในระนาบดิ่ง เช่น แกว่งวัตถุที่ผูกติดปลายเชือกให้เคลื่อนที่เป็นวงกลมในระนาบดิ่ง ลักษณะของการเคลื่อนที่จะเป็นดังภาพ แรงลัพธ์ของแรงดึงเชือก T และน้ำหนักของวัตถุ mg ทำหน้าที่เป็นแรงสู่ศูนย์กลาง Fc ทำให้วัตถุเคลื่อนที่เป็นวงกลมรัศมี r ด้วยอัตราเร็ว v โดยที่ Fc = mv2/r
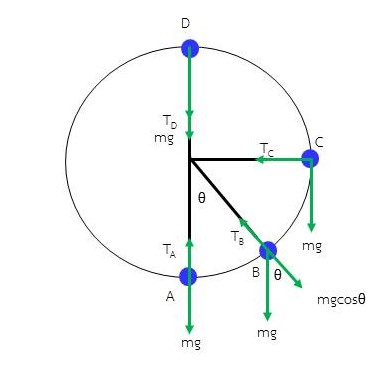
ภาพที่ 3 การเคลื่อนที่แบบวงกมในระนาบดิ่ง
ที่มา : กัญญา เกื้อกูล
จากภาพที่ 3 เราสามารถหาค่าของแรงดึงเชือก T ที่ตำแหน่งต่าง ๆ ได้ดังนี้
ที่ตำแหน่ง A
TA –mg = mv2/r
TA = mv2/r + mg
ที่ตำแหน่ง B
TB –mgcos θ = mv2/r
TB = mv2/r + mgcos θ
ที่ตำแหน่ง C
TC = mv2/r
ที่ตำแหน่ง D
TD +mg = mv2/r
TD = mv2/r – mg
จากการหาค่าแรงตึงเชือก T ที่ตำแหน่งต่าง ๆ ของวงกลม จะพบว่าที่ตำแหน่งต่างมีค่าแรงตึงเชือก T ไม่เท่ากัน แรงตึงเชือกที่จุดต่ำสุดมีค่ามากที่สุด ที่จุดสูงสุดมีค่าน้อยที่สุด และอัตราเร็วของการเลื่อนที่ v ไม่สามารถรักษาให้คงตัวได้ต้องเป็นไปตามหลักการอนุรักษ์พลังงานโดย v จะมากที่สุดที่ตำแหน่ง A และลดลงจนน้อยที่สุดที่ D และอัตราเร็วน้อยที่สุดที่ตำแหน่ง D ที่ทำให้วัตถุสามารถเคลื่อนที่เป็นวงกลมได้ครบรอบพอดี โดยแรงตึงในเส้นเชือก T = 0 หาได้จาก
TD +mg = mv2/r
0 +mg = mv2/r
vmin = (rg)1/2
ตัวอย่างที่ 2 ข้อใดกล่าวถูกต้อง และข้อใดกล่าวผิด เกี่ยวกับการแกว่งวัตถุให้เคลื่อนที่แบบวงกลมในแนวดิ่ง
2.1 น้ำหนักของวัตถุไม่มีผลต่อแรงตึงเชือก
ตอบ ผิด เพราะ น้ำหนักของวัตถุมีผลต่อขนาดของแรงตึงเชือก ถ้าเชือกไม่อยู่ในแนวระดับ
2.2 อัตราเร็วของวัตถุคงตัว
ตอบ ผิด เพราะอัตราเร็วของวัตถุไม่คงตัว เป็นไปตามกฎการอนุรักษ์พลังงาน
2.3 ที่จุดสูงสุดแรงตึงเชือกมีค่ามากที่สุด
ตอบ ผิด เพราะ ที่จุดสูงสุดแรงตึงเชือกมีค่าน้อยที่สุด
2.4 ที่จุดต่ำสุดแรงตึงเชือกมีค่าน้อยที่สุด
ตอบ ผิด เพราะ ที่ต่ำสูงสุดแรงตึงเชือกมีค่ามากที่สุด
2.5 อัตราเร็วน้อยที่สุดที่ทำให้วัตถุสามารถเคลื่อนที่เป็นวงกลมได้ครบรอบพอดี ไม่ขึ้นอยู่กับมวลของวัตถุ
ตอบ ถูกต้อง เพราะ อัตราเร็วน้อยที่สุด vmin ที่ทำให้วัตถุสามารถเคลื่อนที่เป็นวงกลมได้ครบรอบ
พอดี ขึ้นอยู่กับรัศมีของวงกลม r และ ค่าความโน้มถ่วง g
2.6 ขนาดแรงตึงเชือกคงตัวเท่ากับ mv2/r
ตอบ ผิด เพราะ ขนาดแรงตึงเชือกไม่คงตัว ขึ้นอยู่กับตำแหน่งของวัตถุ
แหล่งที่มา
กฤตนัย(สมชาย) จันทรจตุรงค์. (2558). ฟิสิกส์:เรื่องที่ 6 การเคลื่อนที่แบบโปรเจคไตล์และวงกลม. นนทบุรี:ธรรมบัณฑิต.
จรัญ บุระตะ. (2558). คู่มือ เรียนรู้ด้วยตนเอง (Self Study) ฟิสิกส์ ม.4-6 เล่ม 1. กรุงเทพ:นิพนธ์.
Caroline Lowbridge. (2015, June 2). Retrieved October 13, 2018, from https://www.bbc.com/news/uk-england-stoke-staffordshire-32972169
กลับไปที่เนื้อหา
การเคลื่อนที่บนทางโค้ง
เมื่อเรานั่งอยู่ในรถแล้วรถคันนั้นมีการเลี้ยว เราจะมีความรู้สึกว่ามีแรงมากระทำต่อตัวเราในแนวที่มีทิศพุ่งออกจากจุดศูนย์กลางความโค้งของการเลี้ยว

ภาพที่ 1 การเคลื่อนที่ของรถจักรยานยนต์บนทางโค้ง
ที่มา : https://unsplash.com/photos/HHunRG19kF8 , //unsplash.com/@jneric">Joe Neric
การเคลื่อนที่บนทางโค้งราบของรถยนต์

ภาพที่ 2 การเคลื่อนที่ของรถยนต์บนทางโค้ง
ที่มา : https://unsplash.com/photos/0EEckXvEsSM , Alex Holyoake
จากภาพที่ 2 รถยนต์ที่เคลื่อนที่เป็นทางโค้งผลของการเลี้ยวทำให้ผู้โดยสารหรือวัตถุที่อยู่ในรถมีสภาพการเคลื่อนที่เปลี่ยนแปลงไป ซึ่งจากกฎการเคลื่อนที่ข้อ 1 ของนิวตัน วัตถุทั้งหลายจะพยายามรักษาสภาพการเคลื่อนที่ของตัวเอง ผู้โดยสารหรือวัตถุที่อยู่ข้างในรถจะพยายามรักษาสภาพการเคลื่อนที่ของตน โดยพยายามเคลื่อนที่ต่อไปเป็นเส้นตรงตามแนวเดิม ผู้โดยสารหรือวัตถุจึงพยายามกลับเข้าหาแนวการเคลื่อนที่เดิม ทำให้ผู้โดยสารหรือวัตถุในรถมีความรู้สึกว่ามีแรงมากระทำในทิศพุ่งออกจากจุดศูนย์กลาง การที่รถยนต์สามารถเลี้ยวตามความโค้งของถนนได้โดยไม่ไถลออกไปนอกถนนทั้ง ๆ ที่รถพยายามรักษาสภาพการเคลื่อนที่นั้น เป็นเพราะถนนออกแรงเสียดทานกระทำต่อรถ โดยแรงเสียดทานนี้คือแรงเสียดทาน หรืออาจจะเป็นแรงเสียดทานสถิต
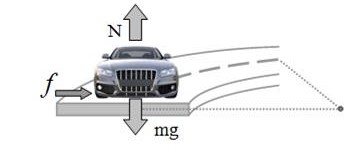
ภาพที่ 3 การเคลื่อนที่ของรถยนต์บนทางโค้ง
ที่มา : www.digitalschool.club/digitalschool/physics2_2_2/physics1/lesson4/index4.php
จากภาพที่ 3 แรง fs ทำหน้าที่เป็นแรงสู่ศูนย์กลาง fs = Fc เราสามารถหาขนาดความเร็วของรถยนต์ที่ทำให้รถวิ่งเข้าโค้งได้อย่างปลอดภัยได้ดังนี้
จาก fs = Fc
0 < fs ≤ μsN
จะได้ 0 < Fc ≤ μsN
0 < fs ≤ μsN
0 < mv2/r ≤ μsmg
0 < v2/rg ≤ μs
0 < v ≤ (μsrg)1/2
การเลี้ยวของรถจักรยาน
เมื่อรถจักรยานหรือจักรยานยนต์เลี้ยวโค้ง ผู้ขับขี่ต้องเอียงตัวรถเป็นมุมค่าหนึ่ง มิฉะนั้นจะเกิดโมเมนต์เนื่องจากแรงปฏิกิริยาจากพื้นมากระทำแก่ตัวรถ ซึ่งจะทำให้รถล้มได้ ดังนั้นจึงมีแรงที่พื้นกระทำต่อรถจักรยานเมื่อมีการเลี้ยว ซึ่งมีด้วยกัน 2 แรง ได้แก่
1) แรงปฏิกิริยาในแนวตั้งฉากกับพื้น N แรงนี้มีสาเหตุมาจากการที่จักรยานออกแรงกดถนน
2) แรงเสียดทาน f แรงนี้มีสาเหตุจากการที่รถจักรยานพยายามรักษาสภาพการเคลื่อนที่ของตัวเองทำให้รถจักรยานพยายามพุ่งกลับไปยังแนวการเคลื่อนที่เดิมในแนวที่ออกจากจุดศูนย์กลางแรง R คือ แรงลัพธ์ของแรง f และ N
จะเห็นได้ว่า ถ้าคนขับไม่เอียงตัวรถให้ทำมุมกับแนวดิ่ง จะทำให้ระยะตั้งฉากจากจุดศูนย์กลางมวลของคนและจักรยานกับแนวแรง R ไม่เป็นศูนย์ทำให้โมเมนต์เนื่องจากแรงลัพธ์ของแรง f และ N รอบจุดศูนย์กลางมวลของรถจักรยานทำให้จักรยานล้มลง
ในการเลี้ยวรถจักรยานผู้ขับขี้จึงจำเป็นต้องเอียงตัวรถจนทำให้แนวแรงลัพธ์ R มีทิศผ่านจุดศูนย์กลางมวล ดังภาพ โดยโมเมนต์ของแรงเท่ากับผลคูณระหว่างขนาดของแรงกับระยะทางตั้งฉากจากจุดหมุนถึงแรงนั้น ดังนั้นเมื่อแนวแรง R มีทิศพุ่งผ่านจุดศูนย์กลางมวลแล้ว ระยะทางตั้งฉากจากจุดหมุน ซึ่งก็คือจุดศูนย์กลางมวล ถึงแนวแรง R จะมีค่าเป็นศูนย์ทำให้โมเมนต์ของแรง R รอบจุดศูนย์กลางมวลก็จะมีค่าเป็นศูนย์จึงเลี้ยวจักรยานได้โดยไม่ล้ม
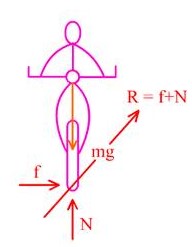
ภาพที่ 4 รถจักรยานกำลังเคลื่อนที่เลี้ยวโค้ง
ที่มา : http://www.atom.rmutphysics.com/charud/oldnews/0/286/5/cir-mo/index4.5.htm
จากภาพที่ 4 จะเห็นได้ว่าเมื่อเอียงทำมุม θ กับแนวดิ่ง แรงปฏิกิริยา R ก็มีทิศทำมุม θ กับแนวดิ่งไปด้วยจึงสามารถแตกแรง R นี้เป็น
แรงในแนวราบ = Rsinθ = แรงเสียดทาน f
และ แรงในแนวดิ่ง = Rcosθ = แรงปฏิกิริยา N
เนื่องจากรถจักรยานไม่มีการเคลื่อนที่ในแนวดิ่งทำให้จักรยานสมดุลในแนวนี้ และเพราะว่ามีแรงกระทำต่อจักรยานในแนวดิ่ง 2 แรง ได้แก่ น้ำหนัก mg ทิศลง และแรง Rcosθ ทิศขึ้น
ดังนั้น Rcosθ = mg ……………(1)
แต่จักรยานเคลื่อนที่เป็นวงกลมในแนวราบโดยมีแรง Rsinθ มากระทำในแนวนี้เพียงแรงเดียวทำให้จักรยานไม่สมดุลในแนวราบ
จากสมการ F = ma
จะได้ Rsinθ = mv2/r ………….(2)
(2)/(1) จะได้ tanθ = v2/rg
จากสมการข้างต้นจะเห็นว่า มุมที่รถจะต้องเลี้ยวนั้นขึ้นอยู่กับอัตราเร็วของรถและรัศมีความโค้งของถนน
การวิ่งของรถยนต์บนถนนยกระดับ
วัตถุที่เคลื่อนที่เป็นวงกลมจะพยายามรักษาสภาพการเคลื่อนที่ของตนด้วยการพยายามเคลื่อนที่ต่อไปเป็นแนวเส้นตรงวัตถุจึงมีแนวโน้มที่จะไถลกลับไปยังแนวเส้นทางการเคลื่อนที่เดิม ดังนั้นการขับรถไปตามทางโค้งจึงค่อนข้างอันตรายเพราะรถอาจจะแฉลบออกนอกถนนได้
ดังนั้นในการสร้างถนนสามารถลดอันตรายได้ โดยการยกระดับถนนให้เอียงทำมุมกับพื้นราบ ซึ่งจะทำให้รถที่มีความเร็วที่เหมาะสมสามารถเลี้ยวผ่านไปได้โดยไม่เกิดอันตรายถึงแม้ว่าถนนนั้นจะไม่มีแรงเสียดทาน (กรณีฝนตก ถนนลื่น)
การคำนวณหามุมในการยกถนนได้ดังนี้
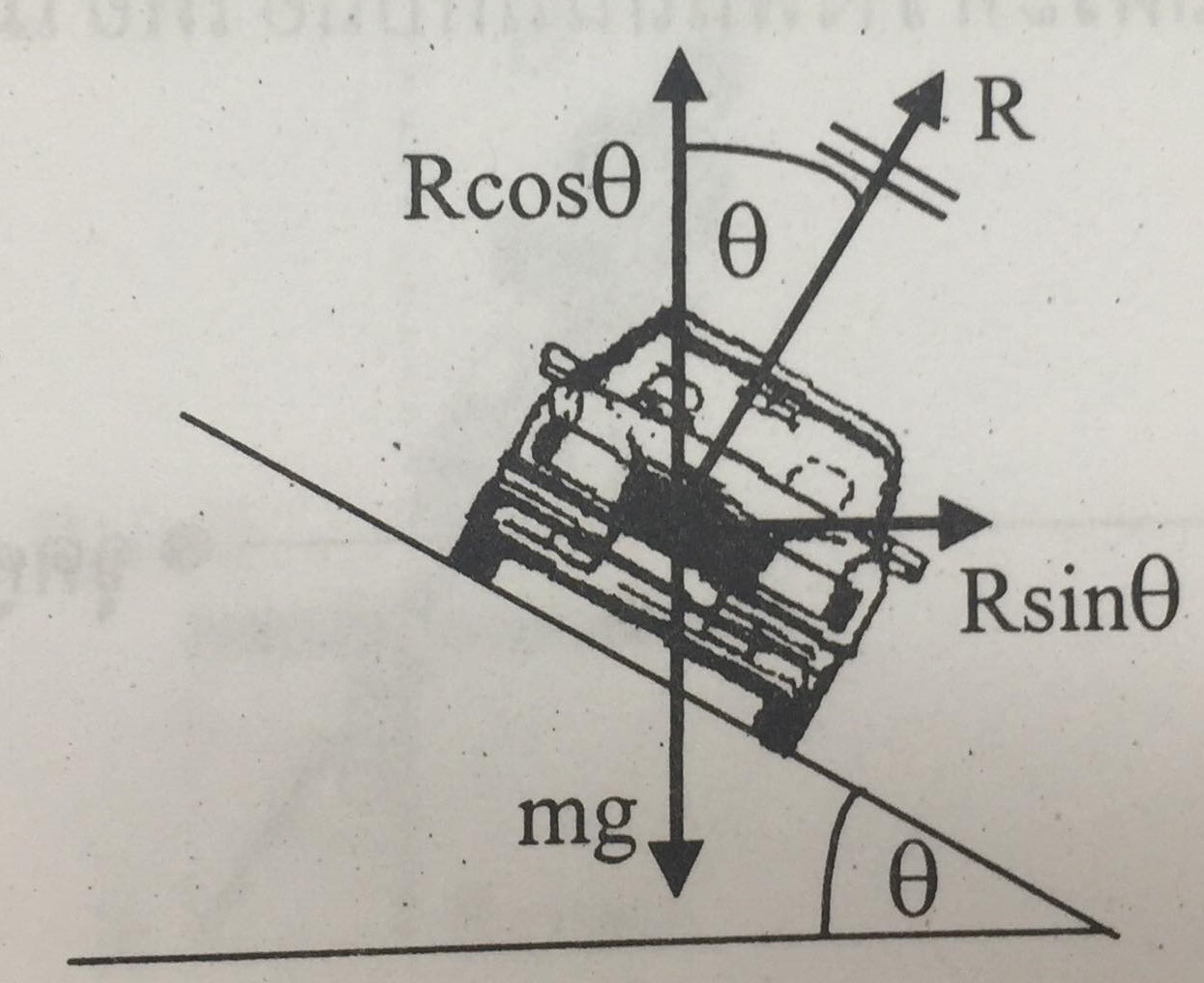
ภาพที่ 5 การเคลื่อนที่ของรถยนต์บนพื้นยกระดับ
ที่มา : ณสรรค์ ผลโภค
จากภาพที่ 5 R เป็นแรงปฏิกิริยาที่พื้นถนนกระทำต่อรถ เพื่อตอบสนองต่อการที่รถออกแรงกดถนนในแนวที่ตั้งฉากกับผิวสัมผัส เพราะว่าแรง R ตั้งฉากกับผิวถนน จึงแตกแรง R ออกได้เป็น
แรงในแนวราบ = Rsinθ
และ แรงในแนวดิ่ง = Rcosθ
เนื่องจากรถไม่มีการเคลื่อนที่ในแนวดิ่งรถจึงสมดุลในแนวนี้
ทำให้ Rcosθ = mg ………(1)
และรถเคลื่อนที่เป็นวงกลมในแนวราบ โดยมีแรง Rsinθ เป็นแรงสู้ศูนย์กลาง
ทำให้ Rsinθ = mv2/r …………(2)
(2)/(1) จะได้ tanθ = v2/rg
จากสมการ รถที่มีอัตราเร็วพอเหมาะหรือต่ำกว่า สามารถเคลื่อนที่เป็นทางโค้งรัศมี r ไปตามถนนที่เอียงทำมุม θ กับแนวระดับได้อย่างไม่ลื่นไถลแม้ถนนจะลื่น
แหล่งที่มา
จรัญ บุระตะ. (2558). คู่มือ เรียนรู้ด้วยตนเอง (Self Study) ฟิสิกส์ ม.4-6 เล่ม 1. กรุงเทพ: นิพนธ์.
ณสรรค์ ผลโภค. (2559). ฟิสิกส์ เล่ม 1 กลศาสตร์. กรุงเทพ: Science center.
กลับไปที่เนื้อหา
-
9414 การเคลื่อนที่แบบต่าง ๆ (โพรเจกไทล์,วงกลม,ทางโค้ง) /lesson-physics/item/9414-2018-11-14-08-28-11เพิ่มในรายการโปรด


