แนวคิดเชิงคำนวณ
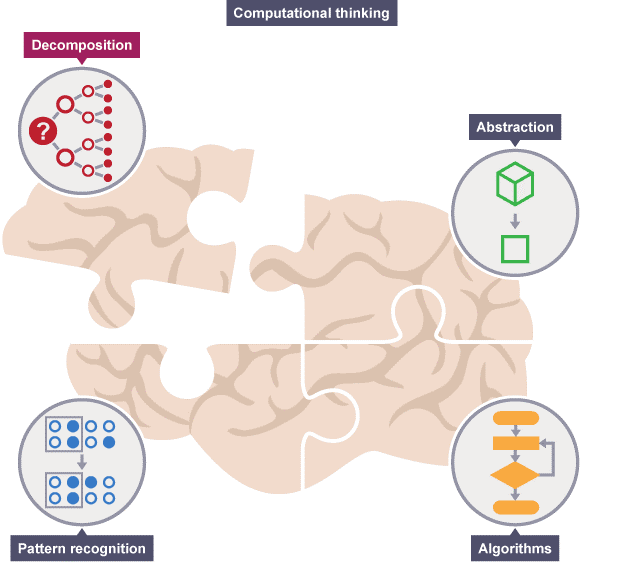
แนวคิดเชิงคำนวณ (Computational Thinking)
การแยกส่วนประกอบ และการย่อยปัญหา (Decomposition)
แนวคิดเชิงคำนวณ (Computational Thinking) เป็นกระบวนการวิเคราะห์ปัญหา เพื่อให้ได้แนวทางหาคำตอบอย่างเป็นขั้นตอนที่สามารถนำไปปฏิบัติได้โดยบุคคลหรือคอมพิวเตอร์อย่างถูกต้อง การคิดเชิงคำนวณ เป็นกระบวนการแก้ปัญหาในหลากหลายลักษณะ เช่น การจัดลำดับเชิงตรรกศาสตร์ การวิเคราะห์ข้อมูล และการสร้างสรรค์วิธีแก้ปัญหาไปทีละขั้น รวมทั้งการย่อยปัญหาที่ช่วยให้รับมือกับปัญหาที่ซับซ้อนหรือมีลักษณะเป็นคำถามปลายเปิดได้วิธีคิดเชิงคำนวณ จะช่วยทำให้ปัญหาที่ซับซ้อนเข้าใจได้ง่ายขึ้น เป็นทักษะที่เป็นประโยชน์อย่างยิ่งต่อทุก ๆ สาขาวิชา และทุกเรื่องในชีวิตประจำวันซึ่งไม่ได้จำกัดอยู่เพียงการคิดให้เหมือนคอมพิวเตอร์แต่เป็นกระบวนการคิดแก้ปัญหาของมนุษย์ เพื่อสั่งให้คอมพิวเตอร์ทำงานและช่วยแก้ปัญหาตามที่เราต้องการได้อย่างมีประสิทธิภาพ
แนวคิดเชิงคำนวณมีองค์ประกอบที่สำคัญ 4 ส่วน ได้แก่ การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) การพิจารณารูปแบบ (Pattern Recognition) การคิดเชิงนามธรรม (Abstraction) การออกแบบอัลกอริทึม (Algorithm) ในบทเรียนนี้จะกล่าวเพียง การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) เท่านั้น โดยมีรายละเอียดดังนี้
ภาพที่ 1 แนวคิดเชิงคำนวณ
ที่มา https://www.bbc.co.uk/bitesize/guides/zqqfyrd/revision/1, BBC
การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition)
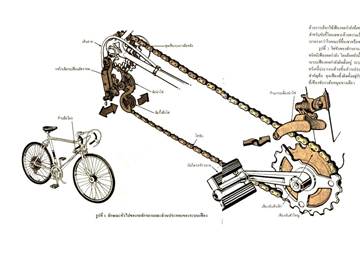
เป็นการแยกส่วนประกอบเป็นวิธีคิดรูปแบบหนึ่งของแนวคิดเชิงคำนวณ เป็นการพิจารณาเพื่อ แบ่งปัญหาหรืองานออกเป็นส่วนย่อย ทำให้สามารถ จัดการกับปัญหาหรืองานได้ง่ายขึ้น การแตกปัญหาที่ซับซ้อนให้เป็นปัญหาย่อยที่มีขนาดเล็กลงและซับซ้อนน้อยลง เพื่อช่วยให้การวิเคราะห์และออกแบบวิธีการแก้ปัญหาทำได้ง่ายขึ้น ในการเขียนโปรแกรมคอมพิวเตอร์ เช่น การเขียนโปรแกรมแยกเป็นส่วน ๆ แยกเป็นแพ็กเกจ แยกเป็นโมดูล หรือมองเป็น layer หรือการแบ่งปัญหาเมื่อจะแก้ไขอุปกรณ์ เช่น การแยกส่วนประกอบของพัดลม แบ่งเป็นใบพัด มอเตอร์ ตะแกรงหน้า ขอบตะแกรง ฝาครอบ ฐานพัดลม เป็นต้น หรือ การแยกส่วนประกอบของรถจักรยาน แบ่งเป็น ล้อหน้า ล้อหลัง หลังอาน โซ่ โช๊ค แฮนด์ มือเบรก เป็นต้น ถ้ามองในรายละเอียดของล้อจักรยานจะเห็น ว่าประกอบด้วย ยางล้อ วงล้อ และซี่ลวด หรือถ้าพิจารณาชุด ขับเคลื่อนก็จะพบว่าประกอบด้วยเฟือง โซ่ และบันได เป็นต้น
ภาพที่ 2 องค์ประกอบของจักรยาย
ที่มา หนังสือเรียน สสวท.
การแก้ปัญหาที่มีความซับซ้อนทำได้ยาก การแบ่งปัญหาใหญ่ให้เป็นปัญหาย่อย ๆ ทำให้มีความซับซ้อนของปัญหาลดลง ช่วยให้การวิเคราะห์และพิจารณารายละเอียดขอปัญหาทำได้อย่างถี่ถ้วน ส่งผลให้สามารถออกแบบขั้นตอนการแก้ปัญหาย่อยแต่ละปัญหาได้ง่ายขึ้น
กรณีตัวอย่างการแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition)
1. รถของกวิน
กวิน เป็นคุณครูที่เด็ก ๆ รัก และกำลังจะเดินทางไปโรงเรียนในเช้าของวันนี้ แต่ด้วยกวินไม่สามารถสตาร์ทรถยนต์คู่ใจที่ใช้ทุกวันให้ติดได้ เนื่องจากเกิดปัญหา 3 ปะการ ได้แก่ เมื่อคืนเปิดไฟในรถทิ้งไว้ทั้งคืนอาจจะทำให้แบตเตอรี่หมด หรือ ก่อนเข้าบ้านเขาไม่ได้เติมน้ำมันให้เต็มถัง อาจจะเป็นไปได้ว่าน้ำมันในถังเชิงเพลิงหมด หรืออาจจะเป็นปัญหาเครื่องยนต์ เมื่อกวินต้องการใช้แนวคิดเชิงคำนวณแก้ปัญหาที่เกิดขึ้น กวินจะสามารถแก้ปัญหาด้วยการแบ่งปัญหาใหญ่เป็นปัญหาย่อย ได้ดังนี้
การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition)
1. แบตเตอรี่หมด
2. น้ำมันเชื้อเพลิงหมด
3. เครื่องยนต์มีปัญหา
ภาพที่ 3 รถของครูกวิน
ที่มา https://www.freepik.com/free-vector/car-dealer-showing-new-red-sports-auto_1311576.htm#page=4&query=car+people&position=27, iconicbestiary
2. การพาจรวดไปดาวอังคาร
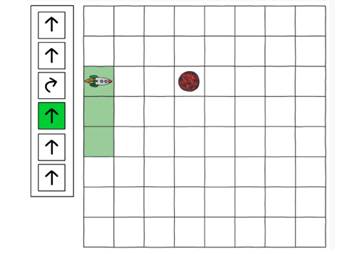
จากเว็บไซต์ https://csunplugged.org/en/topics/kidbots/unit-plan/sending-a-rocket-to-mars/ เป็นกิจกรรมที่จะให้จรวดเดินทางไปดาวอังคาร โดยใช้ลูกศรในการเดิน การหมุน เพื่อทำภาระกิจพิชิตดาวอังคารให้สำเร็จ เพื่อฝึกกระบวนการคิดเป็นขั้นตอนของผู้เรียน และกระบวนการแก้ปัญหา
ภาพที่ 4 ส่งจรวดไปดาวอังคาร
ที่มา https://csunplugged.org/en/topics/kidbots/unit-plan/sending-a-rocket-to-mars, csunplugged.org
ในชีวิตประจำวันของเรา เราไม่ได้ให้คำแนะนำตามที่กล่าวไว้ว่า "เลี้ยวขวา ก้าวไปข้างหน้า ก้าวไปข้างหน้าอีก แล้วก้าวเลี้ยวขวา" คนส่วนใหญ่จะบอกว่าตรงไปที่ดาวอังคาร แต่เมื่อเขียนโปรแกรมจะต้องเจาะจงรายละเอียดการเดินทางไปดาวอังคารมากกว่าปกติ เพราะต้องบอกคอมพิวเตอร์ว่าจะทำอย่างไรในแต่ละขั้นตอน นอกจากนี้การสั่งให้โปรแกรมทำงานตามที่เราต้องการโดยระบุรายละเอียดแล้ว แทนที่จะพยายามแก้ไขปัญหาทั้งหมด จะเห็นได้ว่าเกมส่งจรวดไปดาวอังคาร ยังมีการแบ่งการเขียนโปรแกรมออกเป็นส่วนย่อย ๆ ทำให้งานมีน้อยลง ก็จะสามารถทำให้ถึงจุดหมายได้อย่างรวดเร็วขึ้น เช่น
การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition)
1. เดินตรงไป 2 ช่อง
2. เลี้ยวขวา
3. เดินตรงไป 3 ช่อง
3. พัดลม
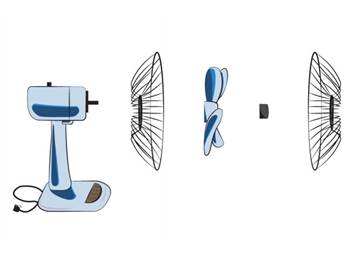
นอกจากการเขียนโปรแกรมสิ่งของในชีวิตประจำวันเช่น จะเรียนรู้ว่าพัดลมทำงานอย่างไร ก็ให้พิจารณาแยกชิ้นส่วนของพัดลมว่ามีอะไรบ้างและศึกษาทีละชิ้น
ภาพที่ 5 ส่วนประกอบพัดลม
https://www.baanlaesuan.com/45800/maintenance/fan, สุพจน์ เพชรศักดิ์วงศ์
การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) ของพัดลม
1. มอเตอร์พร้อมกะโหลกหลังและฐานพัดลม
2. ตะแกรงหลัง
3. ใบพัด
4. ตะแกรงหน้า
4. การเดินทาง
หากจะเดินทางไปเที่ยวหัวหิน จะมีการวางแผนเดินทางอย่างไร ซึ่งอาจแยกย่อยวิธีเดินทางเป็น 4 รูปแบบ เช่น ขับรถไปเอง นั่งรถทัวร์ นั่งรถตู้ หรือนั่งรถไฟ จากนั้นก็มาวิเคราะห์ถึงข้อดีข้อเสียแต่ละวิธีการ
ภาพที่ 6 การเลือกการเดินทาง
ที่มา https://www.freepik.com/free-vector/city-transport-with-bike-car-bus-tram-symbols-isometric-vector-illustration_3997940.htm#page=2&query=transportation&position=30, macrovector
การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) ของพัดลม
1. ขับรถไปเอง
2. นั่งรถทัวร์
3. นั่งรถตู้
4. นั่งรถไฟ
วิเคราะห์ถึงข้อดีข้อเสียแต่ละวิธีการรวมถึงการคำนวณค่าใช้จ่ายของแต่ละวิธีการเดินทางเพื่อเลือกการเดินทางที่ดีที่สุด
แนวคิดเชิงคำนวณ ที่เกี่ยวข้องกับการแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) นั้นเป็นการแตกปัญหาที่ซับซ้อนให้เป็นปัญหาย่อยที่มีขนาดเล็กลงและซับซ้อนน้อยลง เพื่อช่วยให้การวิเคราะห์และออกแบบวิธีการแก้ปัญหาทำได้ง่ายขึ้นทำให้คิดอย่างเป็นระบบมากยิ่งขึ้น โดยผ่านการแยกย่อยปัญหาต่าง ๆ เนื่องด้วยกระบวนงานบางกระบวนงาน มีวิธีการที่ทำงานอย่างเป็นขั้นตอน และมีระบบย่อย จึงมีความจำเป็นที่ต้องแยกปัญหานั้นออกมาเป็นส่วนย่อย ๆ เพื่อสามารถศึกษาปัญหาของกระบวนการได้ชัดเจนยิ่งขึ้น
แหล่งที่มา
ชาญวิทย์ ศรีอุดม. (2562, 12 สิงหาคม). แนวคิดเชิงคำนวณ. สืบค้นเมื่อ 12 สิงหาคม 2562. จาก http://charnwit.in.th/?p=1302#.XX8Q4dUzbIU.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). เทคโนโลยี (วิทยาการคำนวณ). สำนักพิมพ์จุฬาลงกรณ์ : กรุงเทพมหานคร.
csunplugged.org. (2562, 12 สิงหาคม). กิจกรรมส่งจรวดไปดาวอังคาร สืบค้นเมื่อ 12 สิงหาคม 2562, จาก https://csunplugged.org/en/topics/kidbots/unit-plan/sending-a-rocket-to-mars.
Tim Bell, Ian H. Witten and Mike Fellows. (2562). ซีเอส อันปลั๊กโปรแกรมเสริมสมรรถนะและขยายความสามารถของเด็กระดับประถมศึกษา. สถาบันเทคโนโลยีนานาชาติสิรินธร มหาวิทยาลัยธรรมศาสตร์ : ปทุมธานี
กลับไปที่เนื้อหา
การออกแบบอัลกอริทึม (Algorithm)
แนวคิดเชิงคำนวณ (Computational Thinking) เป็นกระบวนการวิเคราะห์ปัญหา เพื่อให้ได้แนวทางหาคำตอบอย่างเป็นขั้นตอนที่สามารถนำไปปฏิบัติได้โดยบุคคลหรือคอมพิวเตอร์อย่างถูกต้อง การคิดเชิงคำนวณ เป็นกระบวนการแก้ปัญหาในหลากหลายลักษณะ เช่น การจัดลำดับเชิงตรรกศาสตร์ การวิเคราะห์ข้อมูล และการสร้างสรรค์วิธีแก้ปัญหาไปทีละขั้น รวมทั้งการย่อยปัญหาที่ช่วยให้รับมือกับปัญหาที่ซับซ้อนหรือมีลักษณะเป็นคำถามปลายเปิดได้วิธีคิดเชิงคำนวณ จะช่วยทำให้ปัญหาที่ซับซ้อนเข้าใจได้ง่ายขึ้น เป็นทักษะที่เป็นประโยชน์อย่างยิ่งต่อทุก ๆ สาขาวิชา และทุกเรื่องในชีวิตประจำวันซึ่งไม่ได้จำกัดอยู่เพียงการคิดให้เหมือนคอมพิวเตอร์แต่เป็นกระบวนการคิดแก้ปัญหาของมนุษย์ เพื่อสั่งให้คอมพิวเตอร์ทำงานและช่วยแก้ปัญหาตามที่เราต้องการได้อย่างมีประสิทธิภาพ แนวคิดเชิงคำนวณมีองค์ประกอบที่สำคัญ 4 ส่วน ได้แก่ การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) การพิจารณารูปแบบ (Pattern Recognition) การคิดเชิงนามธรรม (Abstraction) การออกแบบอัลกอริทึม (Algorithm) ในบทเรียนนี้จะกล่าวเพียง การออกแบบอัลกอริทึม (Algorithm) เท่านั้น โดยมีรายละเอียดดังนี้
ภาพที่ 1 การออกแบบอัลกอริทึม
ที่มา https://www.wired.com/story/want-to-prove-your-business-is-fair-audit-your-algorithm/,JESSI HEMPEL
การออกแบบอัลกอริทึม (Algorithm) เป็นการพัฒนากระบวนการหาคำตอบให้เป็นขั้นตอนที่บุคคลหรือคอมพิวเตอร์สามารถนำไปปฏิบัติตามเพื่อแก้ปัญหาได้ อีกทั้ง เป็นการพัฒนาแนวทางแก้ปัญหาอย่างเป็นขั้นเป็นตอน เพื่อดำเนินตามทีละขั้นตอนในการแก้ไขปัญหา เช่น เมื่อเราต้องการสั่งคอมพิวเตอร์ให้ทำงานบางอย่าง เราจะต้องเขียนโปรแกรมคำสั่งเพื่อให้คอมพิวเตอร์ทำงานไปตามขั้นตอน ตามแนวทางการแก้ปัญหาเพื่อให้คอมพิวเตอร์ทำงานตอบสนองความต้องการของเรา วิธีคิดนี้ที่เรียกว่าวิธีคิดแบบอัลกอริทึม คอมพิวเตอร์จะทำงานได้ดีเพียงใดนั้น ขึ้นอยู่กับชุดคำสั่งอัลกอริทึมที่เราออกแบบให้มันทำงานนั่นเอง การออกแบบอัลกอริทึมยังเป็นประโยชน์ต่อการคำนวณ การประมวลผลข้อมูลและการวางระบบอัตโนมัติต่าง ๆ
การนำอัลกอริทึมไปใช้แก้ปัญหา ไม่จำกัดเฉพาะการเขียนโปรแกรมคอมพิวเตอร์ แต่สามารถใช้กับปัญหาอื่น ๆ ได้เช่นเดียวกัน เพื่อให้เกิดการใช้ทรัพยากรอย่างมีประโยชน์สูงสุด ซึ่งจำเป็นต้องวางแผนอย่างเป็นระบบ เป็นขั้นตอน จึงจำเป็นต้องอาศัยอัลกอริทึม ด้วย เพื่อให้ทราบถึงขั้นตอนต่าง ๆ และสามารถตัดทอนขั้นตอนที่เกินความจำเป็น อีกทั้งยังสามารถปรับปรุง และเพิ่มเติมขั้นตอนใหม่ เข้าไปได้ ช่วยลดความสับสนขณะทำงานด้วย อีกทั้ง ปัญหาบางปัญหาอาจจะมีอัลกอริทึมในการแก้ปัญหาได้หลายวิธี นอกจากการเขียนคำสั่งให้คอมพิวเตอร์ทำงานตามลำดับขั้นตอนที่เราวางไว้ ในชีวิตประจำวันมนุษย์ก็ล้วนมีแนวคิดการออกแบบขั้นตอนในการแก้ไขปัญหา ทำให้ทราบว่าจะต้องทำอะไรก่อนอะไรหลัง เช่น การแต่งตัวมาโรงเรียน การทำอาหาร การทำงานในชีวิตประจำวัน การเดินทาง เป็นต้น
ภาพที่ 2 การลำดับแต่งตัวมาโรงเรียน
ที่มา https://www.freepik.com/free-vector/hand-drawn-children-back-school-collection_4943651.htm#page=1&query=student%20uniform&position=43, freepik
คุณสมบัติของอัลกอริทึม
1. มีความถูกต้อง (correctness) ความถูกต้องเป็นคุณสมบัติข้อแรกที่สำคัญจะต้องพิจารณา ต้องได้ผลลัพธ์ที่ถูกต้อง ซึ่งถ้าผลลัพธ์ที่ได้จากอัลกอริทึมไม่ถูกต้อง จะถือว่าไม่ใช่อัลกอริทึมที่ดี
2. ใช้เวลาในการปฏิบัติงานน้อยที่สุด (efficiency) อัลกอริทึมที่ดีต้องใช้เวลาในการปฏิบัติงานน้อย มีขั้นตอนในการปฏิบัติงานที่ถูกต้อง
3. ต้องมีลำดับขั้นตอนที่ชัดเจน ในการประมวลผลชุดคำสั่งต่าง ๆ ที่ถูกกำหนดด้วยกฎเกณฑ์ในการแก้ปัญหาของ อัลกอริทึม จะต้องประมวลผลเป็นลำดับตามขั้นตอน เพราะการแก้ปัญหาด้วยคอมพิวเตอร์จะต้อง มีลำดับขั้นตอนที่แน่นอน ซึ่งแต่ละขั้นตอนของอัลกอริทึมจะต้องทำหน้าที่อย่างชัดเจนและต่อเนื่องโดยการเริ่มต้นทำงานแต่ละขั้นตอนมีการรับและส่งข้อมูลต่อเนื่องกันไปจนสิ้นสุดการทำงาน ถ้าลำดับไม่ดีอาจจะทำให้การประมวลผลผิดพลาดได้
4. ใช้เนื้อที่ในหน่วยความจำน้อยที่สุด เนื้อที่ในหน่วยความจำจะถูกใช้สำหรับเก็บค่าของตัวแปร และเก็บคำสั่งที่ใช้ในการทำงาน ดังนั้น ถ้าอัลกอริทึมยาวเกินความจำเป็น จะทำให้ใช้เนื้อที่มาก และ ถ้ามีตัวแปรมากเกินความจำเป็น ก็จะทำให้เสียเนื้อที่ในหน่วยความจำไปด้วย
5. มีความยืดหยุ่นในการใช้งาน
6. ใช้เวลาในการพัฒนาน้อยที่สุด เมื่อนำอัลกอริทึมไปแปลงเป็นโปรแกรมภาษาคอมพิวเตอร์แล้วจะต้องใช้เวลาน้อยที่สุด
7. ง่ายต่อการทำความเข้าใจ (readability) อ่านง่ายเข้าใจลำดับขั้นตอนได้ง่าย มีความชัดเจนของขั้นตอน
เครื่องมือช่วยในการเขียนอัลกอริทึม
การออกแบบอัลกอริทึม เป็นแนวทางในการเขียนโปรแกรม ช่วยให้การเขียนโปรแกรมทำได้ง่ายขึ้น ช่วยให้โปรแกรมมีข้อผิดพลาดน้อยลง นอกจากนี้ยังช่วยตรวจสอบการทำงานของโปรแกรม ทำให้ทราบขั้นตอนการทำงานของโปรแกรมได้อย่างรวดเร็ว โดยไม่ต้องดูจากโปรแกรมจริงในการเขียนอัลกอริทึม มีเครื่องมือช่วยในการเขียนที่นิยมใช้ 3 แบบ คือ
1. บรรยาย (narrative description) เป็นการอธิบายแบบใช้ภาษาที่เราสื่อสารกันทั่วไป เป็นการแสดงขั้นตอนการทำงานในลักษณะการบรรยายเป็นข้อความด้วยภาษาพูดใด ๆ เช่น ภาษาไทย ภาษาอังกฤษ ภาษาญี่ปุ่น หรือ ภาษาจีน เป็นต้น ขึ้นอยู่กับความถนัดของผู้เขียนอัลกอริทึม มักเขียนบรรยายขั้นตอนการทำงานเป็นข้อ ๆ เช่น การต้มบะหมี่กึ่งสำเร็จรูป
1. เทน้ำสะอาดใส่หม้อ และต้มน้ำจนเดือด
2. ฉีกซองและนำบะหมี่กึ่งสำเร็จรูปใส่ลงในหม้อ
3. เทเครื่องปรุงลงในหม้อ
4. ปิดฝา
5. รอประมาณ 3 นาที
6. เทใส่ชามรับประทานได้
2. ผังงาน (flowchart) เป็นการใช้รูปภาพสัญลักษณ์ แทนขั้นตอนการเขียนโปรแกรมช่วยลำดับขั้นตอนการทำงานของโปรแกรม และสามารถนำไปเขียนโปรแกรมได้อย่างถูกต้อง ทำให้ตรวจสอบ และแก้ไขโปรแกรมได้ง่าย เมื่อเกิดข้อผิดพลาดช่วยให้การดัดแปลง แก้ไข ทำได้อย่างสะดวกและรวดเร็ว ผู้อื่นสามารถศึกษาการทำงานของโปรแกรมได้อย่างง่าย และรวดเร็ว มากขึ้น
3. รหัสเทียม (pseudo code) เป็นการเขียนคำอธิบายขั้นตอนการทำงานของโปรแกรม โดยใช้ถ้อยคำผสมระหว่างภาษาอังกฤษและภาษาการเขียนโปรแกรมแบบโครงสร้าง ซึ่งจะช่วยให้ผู้เขียนโปรแกรมสามารถพัฒนาขั้นตอนต่าง ๆ ให้เป็นโปรแกรมได้ง่ายขึ้น ส่วนใหญ่มักใช้คำเฉพาะ (Reserve Word) ที่มีในภาษาการเขียนโปรแกรมและมักเขียนด้วยตัวอักษรตัวใหญ่ รหัสเทียมที่ดี จะต้องมีความชัดเจน สั้น และได้ใจความ ข้อมูลต่าง ๆ ที่ใช้จะถูกเขียนอยู่ในรูปของตัวแปร
ภาพที่ 3 ตัวอย่างรหัสเทียม
ที่มาhttps://www.researchgate.net/figure/Pseudo-Code-Example-of-a-GEC_fig1_220930688, Joshua Adams
การออกแบบอัลกอริทึม ในแนวคิดเชิงคำนวณจึงเป็นการพัฒนากระบวนการหาคำตอบให้เป็นขั้นตอนที่บุคคลหรือคอมพิวเตอร์สามารถนำไปปฏิบัติตามเพื่อแก้ปัญหาได้ อัลกอริทึมที่ดี จะต้องมีความถูกต้อง ต้องมีลำดับขั้นตอนที่ชัดเจน มีความยืดหยุ่นในการใช้งาน ใช้เวลาในการพัฒนาน้อย และง่ายต่อการทำความเข้าใจ เครื่องมือที่จะช่วยให้การเขียนอัลกอริทึมของโปรแกรมทำได้ง่ายขึ้น ช่วยให้โปรแกรมมีข้อผิดพลาดน้อยลง เช่น การเขียนบรรยาย การเขียนผังงาน หรือรหัสเทียม จะช่วยให้อัลกอริทึมมีความถูกต้องแม่นยำ และมีข้อผิดพลาดน้อยลง
แหล่งที่มา
เจ๊ะมาดีนา กรมเมือง. (2562, 12 สิงหาคม). การออกแบบและการเขียนอัลกอริทึม. สืบค้นเมื่อ 12 สิงหาคม 2562, จาก https://sites.google.com/site/computernanajang/bth-reiyn-
hnwy-kar-reiyn-ru-thi-1-kar-xxkbaeb-laea-kar-kheiyn-xal-kx-ri-thum.
รัตนา วงศ์ภูงา. (2562, 12 สิงหาคม). อัลกอริทึม. สืบค้นเมื่อ 12 สิงหาคม 2562, จาก https://sites.google.com/a/wwk.ac.th/googlesites/hnwy-thi-2/xal-kx-ri-thum.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). เทคโนโลยี (วิทยาการคำนวณ). สำนักพิมพ์จุฬาลงกรณ์ : กรุงเทพมหานคร.
csunplugged.org. (2562, 12 สิงหาคม). กิจกรรมส่งจรวดไปดาวอังคาร. สืบค้นเมื่อ 12 สิงหาคม 2562,จาก https://csunplugged.org/en/topics/kidbots/unit-plan/sending-a-rocket-to-mars.
Tim Bell, Ian H. Witten and Mike Fellows. (2562). ซีเอส อันปลั๊กโปรแกรมเสริมสมรรถนะและขยายความสามารถของเด็กระดับประถมศึกษา. สถาบันเทคโนโลยีนานาชาติสิรินธร มหาวิทยาลัยธรรมศาสตร์ : ปทุมธานี
Warayuphat Panumphan. (2562, 12 สิงหาคม). Algorithm. สืบค้นเมื่อ 12 สิงหาคม 2562, จากhttp://jsbg.joseph.ac.th/6150/index.php?option=com_content&view=article&id=95&Itemid=95
กลับไปที่เนื้อหา
การคิดเชิงนามธรรม (Abstraction)
แนวคิดเชิงคำนวณ (Computational Thinking) เป็นกระบวนการวิเคราะห์ปัญหา เพื่อให้ได้แนวทางหาคำตอบอย่างเป็นขั้นตอนที่สามารถนำไปปฏิบัติได้โดยบุคคลหรือคอมพิวเตอร์อย่างถูกต้อง การคิดเชิงคำนวณ เป็นกระบวนการแก้ปัญหาในหลากหลายลักษณะ เช่น การจัดลำดับเชิงตรรกศาสตร์ การวิเคราะห์ข้อมูล และการสร้างสรรค์วิธีแก้ปัญหาไปทีละขั้น รวมทั้งการย่อยปัญหาที่ช่วยให้รับมือกับปัญหาที่ซับซ้อนหรือมีลักษณะเป็นคำถามปลายเปิดได้วิธีคิดเชิงคำนวณ จะช่วยทำให้ปัญหาที่ซับซ้อนเข้าใจได้ง่ายขึ้น เป็นทักษะที่เป็นประโยชน์อย่างยิ่งต่อทุก ๆ สาขาวิชา และทุกเรื่องในชีวิตประจำวันซึ่งไม่ได้จำกัดอยู่เพียงการคิดให้เหมือนคอมพิวเตอร์แต่เป็นกระบวนการคิดแก้ปัญหาของมนุษย์ เพื่อสั่งให้คอมพิวเตอร์ทำงานและช่วยแก้ปัญหาตามที่เราต้องการได้อย่างมีประสิทธิภาพ แนวคิดเชิงคำนวณมีองค์ประกอบที่สำคัญ 4 ส่วน ได้แก่ การแบ่งปัญหาใหญ่เป็นปัญหาย่อย (Decomposition) การพิจารณารูปแบบ (Pattern Recognition) การคิดเชิงนามธรรม (Abstraction) การออกแบบอัลกอริทึม (Algorithm) ในบทเรียนนี้จะกล่าวเพียง การคิดเชิงนามธรรม (Abstraction) เท่านั้น โดยมีรายละเอียดดังนี้
การคิดเชิงนามธรรม (Abstraction)
เป็นองค์ประกอบหนึ่งของแนวคิดเชิงคำนวณ ซึ่งใช้กระบวนการคัดแยกคุณลักษณะที่สำคัญออกจากรายละเอียดปลีกย่อย ในปัญหาหรืองานที่กำลังพิจารณา เพื่อให้ได้ข้อมูลที่จำเป็นและเพียงพอในการแก้ปัญหา เป็นการแยกรายละเอียดที่สำคัญและจำเป็นต่อการแก้ปัญหาออกจากรายละเอียดที่ไม่จำเป็น ซึ่งรวมไปถึงการแทนกลุ่มของปัญหา ขั้นตอน หรือกระบวนการที่มีรายละเอียดปลีกย่อยหลายขั้นตอนด้วยขั้นตอนใหม่เพียงขั้นตอนเดียว โดยจะยกตัวอย่างดังนี้
1. การคิดเชิงนามธรรมที่เกี่ยวข้อกับรูปทรง
ภาพที่ 1 การคิดเชิงนามธรรมที่เกี่ยวข้อกับรูปทรง
ที่มา https://www.youtube.com/watch?v=bAVTLjhDjuw, NativLang
จากรูปภาพดังกล่าวที่เกิดจากรูปทรงกลม ได้แก่ ล้อ ผลส้ม ลูกบาสเก็ตบอล มีลักษณะเป็นรูปทรงกลม การคิดเชิงนามธรรมนี้คือรูปทรงกลม นอกจาก ล้อ ผลส้ม ลูกบาสเก็ตบอล ยังมีวัตถุอื่น ๆ อีกมากมายที่มีลักษะเป็นทรงกล เช่น ฝาขวดน้ำดื่ม ฟุตบอล ลูกปิงปอง เหรียญ เป็นต้น
2. การคิดเชิงนามธรรมที่เกี่ยวข้อกับตัวอักษร
ในหนังสือแบบเรียนวิทยาการคำนวณ ของสถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี ระดับชั้นมัธยมศึกษาปีที่ 1 ได้ยกตัวอย่างคำว่า Hello
ภาพที่ 2 ตัวอักษร Hello
ที่มา หนังสือเรียนวิทยาการคำนวณ ระดับชั้นมัธยมศึกษาปีที่ 1, สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี
Hello แต่ละตัวจะมีรูปแบบที่แตกต่างกันขึ้นอยู่กับประสบการณ์ที่ผู้เขียนแต่ละคนมี จากตัวอย่างจะเห็นรายละเอียดที่แตกต่างกันเช่นสีรูปแบบตัวอักษร อักษรตัวพิมพ์ใหญ่หรือตัวพิมพ์เล็กและรายละเอียดอื่น ๆเช่นการขีดเส้นใต้หรือการเอียงของตัวอักษร โดยรูปแบบที่แต่ละคนมีอยู่ ถ้าจะถ่ายทอดให้ผู้อื่นรับรู้และเข้าใจทุกอย่างแทบจะเป็นไปไม่ได้และอาจจะไม่มีความจำเป็นที่ผู้อื่นต้องรับรู้รายละเอียดทั้งหมด
ในที่นี้หากผู้รับข้อมูลต้องการทราบว่าคำนี้ประกอบไปด้วยอักขระใดบ้างโดยไม่สนใจประเภทของอักษรตัวพิมพ์เล็กหรือพิมพ์ใหญ่คำว่า Hello ทุกตัวในตารางต่างก็มีองค์ประกอบเชิงนามธรรมเดียวกันคือเป็นคำที่ประกอบด้วยอักขระ H e l l และ o แต่ในบางสถานการณ์อาจสื่อว่าข้อมูลดังกล่าวเป็นเพียงอักขระภาษาอังกฤษห้าตัวหรือเป็นคำภาษาอังกฤษเพียงหนึ่งคำ
3. การคิดเชิงนามธรรมจากเกมเลขฐานสอง
ภาพที่ 3 กิจกรรมเลขฐานสอง
ที่มา https://csunplugged.org/en/topics/binary-numbers/unit-plan/how-binary-digits-work, csunplugged
การแสดงเลขฐานสอง (เพียงแค่ใช้ 0 และ 1) เป็นแนวคิดเชิงนามธรรมที่ซ่อนความซับซ้อนของอุปกรณ์อิเล็กทรอนิกส์และฮาร์ดแวร์ภายในคอมพิวเตอร์ที่เก็บข้อมูล สิ่งที่เป็นนามธรรมช่วยให้เราทำให้ง่ายขึ้นเพราะเราสามารถลดทอนต่อรายละเอียดที่เราไม่จำเป็นต้องรู้ ในกรณีนี้รายละเอียดที่เราสามารถละเว้นได้ ได้แก่ : อุปกรณ์คอมพิวเตอร์ เช่น วงจรอิเล็กทรอนิกส์และแรงดันไฟฟ้าในวงจร เพื่อจัดเก็บและย้ายข้อมูล และฟิสิกส์เชิงซ้อนและทฤษฎีทางคณิตศาสตร์ที่เกี่ยวกับคอมพิวเตอร์ เราไม่จำเป็นต้องเข้าใจว่าวงจรเหล่านี้ทำงานอย่างไรเพื่อใช้ข้อมูลและแสดงสิ่งต่าง ๆ โดยใช้เลขฐานสอง การใช้เลขฐานสองเป็นสิ่งที่เป็นนามธรรมของวงจรเหล่านี้และช่วยให้เราสามารถแทนตัวเลขที่ทำจากบิต (0s และ 1s) เพื่อทำความเข้าใจข้อมูลและแก้ไขปัญหาโดยไม่ต้องคิดเกี่ยวกับสิ่งที่เกิดขึ้นภายใต้เครื่องคอมพิวเตอร์ เราสามารถใช้เลขฐานสองเพื่อแสดงข้อมูลทุกประเภทที่เก็บไว้ในคอมพิวเตอร์ เมื่อเราแสดงข้อมูลรูปแบบอื่น ๆ (เช่น ตัวอักษรรูปภาพและเสียง) เรายังใช้นามธรรมเพราะเราซ่อนรายละเอียดของตัวเลขไบนารี่ทั้งหมดที่อยู่ด้านล่างและเพียงแค่ดูข้อมูลทั้งหมด ข้อมูลทุกรูปแบบถูกแสดงเป็นตัวเลข สำหรับข้อความที่เรามีตัวเลขสำหรับตัวอักษรแต่ละตัวสำหรับภาพที่เราใช้ตัวเลขสำหรับแต่ละสีและอื่น ๆ เราใช้สิ่งที่เป็นนามธรรมหลายชั้น การแปลงและเป็นตัวแทนของเลขฐานสองโดยใช้สิ่งอื่น ๆ นอกเหนือจาก“ 1 และ 0 ”,“ ขาวดำ” และ“ ปิดและเปิด” หากคุณสามารถเปลี่ยนคำเช่น "ดำ" และ "ขาว" ด้วย 0 และ 1 โดยที่ผู้เรียนไม่ต้องกังวลเกี่ยวกับความแตกต่างผู้เรียนก็กำลังใช้สิ่งที่เป็นแนวคิดเชิงนามธรรม
4. การคัดแยกรายละเอียดปลีกย่อย
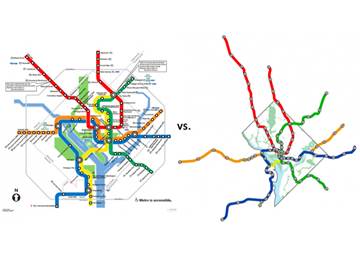
ภาพที่ 4 แผนภาพรถไฟฟ้า
ที่มา https://computersciencewiki.org/index.php/File:Screen_Shot_2017-08-05_at_06.29.05.png, MacKenty
แผนภาพทั้งสองให้ข้อมูลเกี่ยวกับสถานีรถไฟฟ้าและสถานีเชื่อมต่อ แผนภาพด้านซ้ายมือจะแสดงรายละเอียดของสถานี ชื่อสถานนี้ และจุดเชื่อมต่อสถานี แผนภาพด้านขวาจะลดทอนรายละเอียดของสถานีแสดงเฉพาะข้อมูลเส้นทางและการเชื่อมต่อของรถไฟฟ้า ในการใช้แผนภาพทั้งสอง หากผู้ใช้ต้องการทราบตำแหน่งของสถานีรถไฟฟ้าแผนภาพด้านซ้ายมือจะเหมาะสมกว่าแผนภาพขวามือ แต่สำหรับผู้ใช้งานเพื่อการเดินทางในชีวิตประจำวันแผนภาพด้านขวามือจะเหมาะสมกว่า ดังนั้นแบบจำลองที่ดีต้องมีรายละเอียดที่เหมาะสมกับความต้องการการใช้งานของผู้ใช้
5. การอธิบายปัญหาโดยใช้รายละเอียด และแบบซ่อนรายละเอียด
ปัญหาประกอบด้วยรายละเอียดที่หลากหลายโดยมีทั้งรายละเอียดที่จำเป็น และไม่จำเป็นต่อการแก้ปัญหา การคิดเชิงนามธรรมเป็นการคัดแยกรายละเอียดที่ไม่จำเป็นออกจากปัญหาที่พิจารณาอยู่ ทำให้สามารถเข้าใจ วิเคราะห์ และออกแบบวิธีการแก้ปัญหาในภาพรวมได้ง่ายขึ้น การคิดเชิงนามธรรมยังรวมถึงการซ่อนรายละเอียดโดยการแทนกลุ่มของปัญหาขั้นตอนและกระบวนการที่มีรายละเอียดปลีกย่อยหลายขั้นตอน ให้เป็นขั้นตอนเดียว เพื่อให้สามารถอธิบายวิธีแก้ปัญหาได้กระชับขึ้นดังตัวอย่างต่อไปนี้
ภาพที่ 5 บ้าน
การอธิบายปัญหาโดยใช้รายละเอียด
วาดตัวบ้านด้วยสี่เหลี่ยมจัตุรัสสีเหลือง ขนาดด้านละ 50 หน่วย ตั้งอยู่ตำแหน่งมุมล่างซ้ายที่พิกัด (120,90) ด้านบนของสี่เหลี่ยมวาดหลังคาเป็นรูปสามเหลี่ยมด้านเท่าสีเขียวขนาดด้านละ 50 หน่วย
การอธิบายปัญหาแบบซ่อนรายละเอียด
ขนาด 50 หน่วย ตัวบ้านสีเหลือง หลังคาสีเขียว ตั้งอยู่ตำแหน่ง (120,90)
แนวคิดนามธรรมจึงเป็นองค์ประกอบหนึ่งของแนวคิดเชิงคำนวณ ซึ่งใช้กระบวนการคัดแยกคุณลักษณะที่สำคัญออกจากรายละเอียดปลีกย่อย ในปัญหาหรืองานที่กำลังพิจารณา เพื่อให้ได้ข้อมูลที่จำเป็นและเพียงพอในการแก้ปัญหา แนวคิดนามธรรมบางอย่างอาจจะอยู่ในรูปแบบของรูปร่างหรือรูปทรง ความแตกต่าง ความเหมือนรูปแบบอักขระ การแทนสัญลักษณ์ต่าง ๆ เช่น การแทน 0 1 ของเลขฐานสอง การคัดแยกรายละเอียดปลีกย่อยที่ไม่จำเป็นต่อการตัดสินใจหรือการใช้งาน เช่น การใช้แผนที่ การคำนวณระยะทาง การวาดแผนทีการเดินทางไป ณ จุดหมายใดจุดหมายหนึ่ง การเดินทางด้วยรถไฟฟ้า หรือแม้แต่การอธิบายปัญหาโดยใช้รายละเอียดและแบบซ่อนรายละเอียด ล้วนเป็นแนวคิดเชิงนามธรรมที่อยู่ในชีวิตประจำวันทั้งสิ้น
แหล่งที่มา
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). เทคโนโลยี (วิทยาการคำนวณ). สำนักพิมพ์จุฬาลงกรณ์ : กรุงเทพมหานคร.
csunplugged.org. (2562, 12 สิงหาคม). กิจกรรมส่งจรวดไปดาวอังคาร สืบค้นเมื่อ 12 สิงหาคม 2562,จาก https://csunplugged.org/en/topics/kidbots/unit-plan/sending-a-rocket-to-mars.
Tim Bell, Ian H. Witten and Mike Fellows. (2562). ซีเอส อันปลั๊กโปรแกรมเสริมสมรรถนะและขยายความสามารถของเด็กระดับประถมศึกษา. สถาบันเทคโนโลยีนานาชาติสิรินธร มหาวิทยาลัยธรรมศาสตร์ : ปทุมธานี
กลับไปที่เนื้อหา
การพิจารณารูปแบบ (Pattern Recognition)
เป็นการหารูปแบบซึ่งเป็นทักษะการหาความสัมพันธ์ที่เกี่ยวข้อง แนวโน้ม และลักษณะ ทั่วไปของสิ่งต่าง ๆ โดยทั่วไปแล้วผู้เรียนจะเริ่มพิจารณาปัญหาหรือสิ่งที่สนใจ จากนั้นอาจใช้ทักษะการแยกส่วนประกอบทำให้ได้องค์ประกอบภายในอื่น ๆ แล้วจึงใช้ทักษะการหารูปแบบเพื่อสร้างความเข้าใจระหว่างองค์ประกอบเหล่านั้น โดยพิจารณาว่าเคยพบปัญหาลักษณะนี้มาก่อนหรือไม่ หากมีรูปแบบของปัญหาที่คล้ายกันสามารถนำวิธีการแก้ปัญหานั้นมาประยุกต์ใช้ และพิจารณารูปแบบปัญหาย่อยซึ่งอยู่ภายในปัญหาเดียวกันว่ามีส่วนใดที่เหมือนกัน เพื่อใช้วิธีการแก้ปัญหาเดียวกันได้ ทำให้จัดการกับปัญหาได้ง่ายขึ้น และการทำงานมีประสิทธิภาพเพิ่มขึ้น เช่น ในส่วนประกอบของจักรยานผู้เรียนจะพบว่าระบบขับเคลื่อนประกอบด้วยเฟืองหน้า และเฟืองหลังเชื่อมกันด้วยโซ่จักรยานมีลักษณะเหมือนระบบรอก ดังนั้น ถ้านักเรียนทราบถึงคุณสมบัติการทดแรงของระบบรอกดังกล่าว นักเรียนก็จะเข้าใจการทดแรงของระบบขับเคลื่อนของจักรยาน เช่นเดียวกัน ในกรณี การหารูปแบบเกิดขึ้นเมื่อผู้เรียนเปรียบเทียบสิ่งที่สนใจกับสิ่งอื่นที่เคยทราบมาก่อน
ภาพที่ 1 เฟืองหน้าและเฟืองหลัง
http://www.zeedbike.com/article/28/จักรยานหลายเกียร์, zeedbike
แบบรูป (Pattern)
เป็นการแสดงความสัมพันธ์ของสิ่งต่าง ๆ ที่มีลักษณะสำคัญบางอย่างร่วมกันอย่างมีเงื่อนไข ซึ่งสามารถอธิบายความสัมพันธ์เหล่านั้นได้โดยใช้การสังเกต การวิเคราะห์ หาเหตุผลสนับสนุนจนได้บทสรุปอันเป็นที่ยอมรับได้ แบบรูปนับเป็นปัจจัยพื้นฐานอันหนึ่งในการช่วยคิดแก้ปัญหาต่าง ๆ ในชีวิตประจำวันโดยที่เราได้เคยพบเห็นและได้ผ่านการใช้กระบวนการคิดวิเคราะห์ด้วยเหตุด้วยผลกับแบบรูปในลักษณะต่าง ๆ กันมาแล้ว แบบรูปที่จะกล่าวถึงนี้เป็นแบบรูปในลักษณะต่าง ๆ เพื่อให้เห็นรูปแบบของการจัดลำดับ และการกระทำซ้ำอย่างต่อเนื่องเพื่อจะได้ใช้การสังเกต การวิเคราะห์ การให้เหตุผลในการบอกความสัมพันธ์ของ สิ่งต่าง ๆ ที่พบเห็นได้อย่างถูกต้องจนถึงขั้นสรุปเป็นกฎเกณฑ์

ภาพที่ 2 ความสัมพันธ์ของแบบรูป
http://www.tup.ac.th/tup/learning, นาถลดา มนต์ทอง.
โดยทั่วไปในคณิตศาสตร์จะพบเห็นการใช้แบบรูปในเรื่องของจำนวน รูปภาพ รูป เรขาคณิตจากแบบรูปของจำนวนเราสามารถเขียนแสดงความสัมพันธ์โดยใช้ตัวแปร และสมบัติของการเท่ากันสร้างสมการเพื่อใช้แก้ปัญหาได้ จากเงื่อนไขข้างต้น สรุปได้ว่า แบบรูปจึงเป็นรูปร่าง หรือลักษณะของสิ่งต่าง ๆ ที่นำมาประกอบกันตามความสัมพันธ์ระหว่างสิ่งเหล่านั้น
ในทางวิทยาการคำนวณ การหารูปแบบจึงเป็นการหารูปแบบที่เหมือนและแตกต่างกันระหว่างสิ่งของ ต่าง ๆ ที่สนใจหลายชิ้นการพิจารณารูปแบบนี้จะช่วยระบุองค์ประกอบสำคัญร่วมกันของสิ่งของเหล่านั้นได้ซึ่งจะเป็นพื้นฐานในการสร้างความเข้าใจเชิงนามธรรม เช่น เมาส์จะเห็นว่าเมาส์นั้นมีรูปลักษณ์ภายนอกที่แตกต่างกันออกไปแต่สังเกตได้ว่ารูปแบบการใช้งานนั้นเหมือนกัน คือสามารถบังคับตำแหน่งตัวชี้ได้โดยการขยับเมาส์และใช้กดหรือสัมผัสบนปุ่มเมาส์เพื่อกระทำการสิ่งใดสิ่งหนึ่งตามที่โปรแกรมไว้
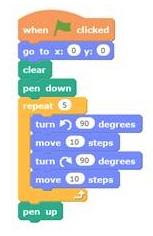
ในการเขียนโปรแกรมแบบ Blockly ด้วยโปรแกรม Scratch หากเราต้องการสร้างรูปบันไดเป็นขั้น ๆ 5 ขั้น หากเราใช้คำสั่ง ดังรูปที่ 3 เราจะต้องเขียนคำสั่งดังกล่าว ถึง 5 ครั้ง ดังรูปที่ 4
ภาพที่ 3 การเขียนโปรแกรมแบบ Blockly
ภาพที่ 4 สร้างรูปบันไดเป็นขั้น ๆ 5 ขั้น
เมื่อเราประยุกต์การพิจารณารูปแบบสำหรับการเขียนโปรแกรมดังกล่าว แล้วใช้คำสั่ง Repeat ช่วย ดังรูปที่ 5 ในการเขียนโปรแกรม ผลปรากฏว่า แทนที่เราจะต้องเขียนโปรแกรมดังรูปที่ 3 ซ้ำกันถึง 5 ครั้ง เราสังเกตเห็นว่า รูปแบบมีลักษณะความสัมพันธ์ที่เกี่ยวข้อง โดยใช้คำสั่ง Repeat และนำรูปแบบโปรแกรมดังรูปที่ 3 เพียง 1 ครั้ง ก็จะได้ผลลัพธ์เช่นเดียวกัน และทำให้โปรแกรมสั้นลงอีกด้วย
ภาพที่ 5 สร้างรูปบันไดเป็นขั้น ๆ 5 ขั้น โดยใช้คำสั่ง Repeat
ดังนั้นการพิจารณารูปแบบ เป็นการหารูปแบบซึ่งเป็นทักษะการหาความสัมพันธ์ที่เกี่ยวข้อง แนวโน้ม และลักษณะ ทั่วไปของสิ่งต่าง ๆ การหารูปแบบเพื่อสร้างความเข้าใจระหว่างองค์ประกอบเหล่านั้น เช่น การจัดหมวดหมู่สัตว์ที่คล้ายคลึงกัน ให้อยู่ในสปีชีส์เดียวกัน เพื่อให้ง่ายต่อการศึกษา การหาพฤติกรรมการบริโภคของคน ว่านิยมซื้ออะไร ช่วงเวลาไหน มีรูปแบบพฤติกรรมซ้ำ ๆ อะไรบ้าง ความสัมพันธ์ของเฟืองหน้า และเฟืองหลัง ของรถจักรยานที่เชื่อมกันด้วยโซ่จักรยานมีลักษณะเหมือนระบบรอก สิ่งของเช่นมาส์นั้นมีรูปลักษณ์ภายนอกที่แตกต่างกันออกไปแต่สังเกตได้ว่ารูปแบบการใช้งานนั้นเหมือนกัน การเขียนโปรแกรมที่ทำซ้ำ ๆ กันหลาย ๆ ครั้ง จะมีลักษณะรูปแบบที่เหมือนกัน รูปแบบของปัญหาที่คล้ายกันสามารถนำวิธีการแก้ปัญหามาประยุกต์ใช้ เพื่อใช้วิธีการแก้ปัญหาเดียวกันได้
แหล่งที่มา
นาถลดา มนต์ทอง. (8 ตุลาคม 2562). แบบฝึกทักษะคณิตศาสตร์ ม.1 เรื่อง แบบรูปและความสัมพันธ์. สืบค้นเมื่อ 8 ตุลาคม 2562, จาก http://www.tup.ac.th/tup/learning.
อนุวัฒน์ พานิพัด. (8 ตุลาคม 2562). แนวคิดเชิงคำนวณ. สืบค้นเมื่อ 8 ตุลาคม 2562,จาก https://www.teachernu.com/2019/01/02/แนวคิดเชิงคำนวณสถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). เทคโนโลยี (วิทยาการคำนวณ). สำนักพิมพ์จุฬาลงกรณ์ : กรุงเทพมหานคร.
Tim Bell, Ian H. Witten and Mike Fellows. (2562). ซีเอส อันปลั๊กโปรแกรมเสริมสมรรถนะและขยายความสามารถของเด็กระดับประถมศึกษา. สถาบันเทคโนโลยีนานาชาติสิรินธร มหาวิทยาลัยธรรมศาสตร์ : ปทุมธานี
กลับไปที่เนื้อหา
การแก้ปัญหา
ในการดำเนินชีวิตประจำวันเรามักประสบกับปัญหาต่าง ๆ เช่น ด้านการเรียน ด้านการทำงาน เมื่อเราเจอปัญหา มนุษย์มักจะดำเนินวิธีการแก้ปัญหาด้วยรูปแบบต่าง ๆ ตามบริบทของปัญหานั้น ๆ โดยแต่ละวิธีการอาจเหมือนหรือแตกต่างกัน ทั้งนี้ขึ้นอยู่กับความรู้ ความสามารถ และประสบการณ์ของแต่ละบุคคล ได้มีการนำวิธีการแก้ปัญหาต่าง ๆ มาวิเคราะห์และสามารถแก้ปัญหานั้นได้ การนำหลักและวิธีการแก้ปัญหาด้วยวิธีการคอมพิวเตอร์ โดยการนำภาษาโปรแกรมคอมพิวเตอร์และเครื่องมือต่าง ๆ มาช่วยในการแก้ปัญหา นั้นมีรายละเอียดดังนี้
หลักการและความหมายการแก้ปัญหา
การแก้ปัญหา หมายถึงกระบวนการการแก้ปัญหาอย่างเป็นระบบ (Systematically) และมีประสิทธิภาพ (Efficiently) สามารถแก้ปัญหาได้รวดเร็ว ใช้ทรัพยากรน้อย โดยศึกษาถึงสาเหตุที่มาของปัญหา ซึ่งจะมีลักษณะแตกต่างกัน และคิดค้นหาวิธีการที่เหมาะสมที่สุดเพื่อจะแก้ไข การคิดหาวิธีการโดยการศึกษาหาความรู้จากแหล่งต่าง ๆ แล้วจึงตัดสินใจเลือกวิธีที่ดีที่สุดในการตัดสินใจนั้น นอกจากวิธีการแก้ปัญหาที่ยกตัวอย่างมาซึ่งได้แก่ วิธีการลองผิดลองถูก การใช้เหตุผล การใช้วิธีขจัด ยังมีวิธีการแก้ปัญหาอีกมากมายที่ผู้แก้ปัญหาสามารถเลือกใช้ให้เข้ากับตัวปัญหาและประสบการณ์ของผู้แก้ปัญหาเอง แต่อย่างไรก็ตาม วิธีการเหล่านั้นล้วนมีขั้นตอนที่คล้ายคลึงกัน และจากการศึกษาพฤติกรรมในการเรียนรู้และแก้ปัญหาของมนุษย์พบว่า โดยปกติมนุษย์มีกระบวนการในการแก้ปัญหา ได้แก่ การวิเคราะห์และกำหนดรายละเอียดของปัญหา การเลือกเครื่องมือและออกแบบขั้นตอนวิธี การดำเนินการแก้ปัญหา การตรวจสอบและการปรับปรุง
ภาพที่ 1 กระบวนการในการแก้ปัญหา 4 ขั้นตอน
ที่มา https://pixabay.com/th/illustrations/ปัญหา-การแก้ปัญหา-ช่วยให้-3303396, Geralt
ขั้นตอนการแก้ปัญหา
- การวิเคราะห์และกำหนดรายละเอียดของปัญหา
การวิเคราะห์และกำหนดรายละเอียดของปัญหา (State the problem) วิเคราะห์และกำหนดรายละเอียดของปัญหา จุดประสงค์ของขั้นตอนนี้ คือ เป็นการทำความเข้าใจเกี่ยวกับรายละเอียดเงื่อนไข ข้อกำหนด รวมถึงข้อจำกัดต่าง ๆ ของปัญหา ข้อมูลที่จำเป็นในการแก้ปัญหา ตรวจสอบว่ามีข้อมูลเพียงพอหรือไม่ จะหาข้อมูลเพิ่มเติมให้ครบถ้วนต่อการใช้แก้ปัญหาได้อย่างไร ข้อมูลผลลัพธ์ที่ได้คืออะไร และจะตรวจสอบความถูกต้องของผลลัพธ์ที่ได้อย่างไร ขั้นตอนนี้เป็นขั้นตอนแรกสุดก่อนที่จะลงมือแก้ปัญหา แต่ผู้แก้ปัญหามักจะมองข้ามความสำคัญของขั้นตอนนี้อยู่เสมอ โดย องค์ประกอบในการวิเคราะห์ปัญหามีดังนี้
- การระบุข้อมูลออก (Output Specification) ต้องพิจารณาเป้าหมาย หรือวัตถุประสงค์ของงานว่าต้องการผลลัพธ์อย่างไร โดยคำนึงถึงผู้ใช้เป็นหลัก เป็นสิ่งที่โจทย์ต้องการในการแก้ปัญหาด้วยคอมพิวเตอร์จำเป็นต้องระบุให้ชัดเจนว่าสิ่งที่ต้องการให้เป็นผลลัพธ์ของปัญหาคืออะไร และต้องการให้แสดงออกในรูปแบบใด เช่น การประมวลผลข้อมูลการเบิกถอนเงินจากเครื่องเอทีเอ็ม ต้องมีการแสดงข้อมูลออกเป็นจำนวนเงินที่ถอนไป และจำนวนเงินคงเหลือในบัญชี อีกทั้งยังต้องออกแบบการจัดวางข้อมูลเหล่านี้เพื่อพิมพ์ลงในใบบันทึกรายการด้วย
- การระบุข้อมูลเข้า (Input Specification) ต้องทราบว่ามีข้อมูลอะไรบ้างที่ต้องป้อนเข้าสู่ระบบคอมพิวเตอร์ ข้อมูลเริ่มต้นหรือเงื่อนไขที่โจทย์กำหนดมาให้ตั้งแต่แรก ในการแก้ปัญหา ผู้แก้ปัญหาจะต้องใช้ข้อมูลเหล่านี้ในการประมวลผู้เพื่อให้ได้ผลลัพธ์ตามที่ต้องการ ตัวอย่าง เช่น การเบิกถอนเงินด้วยบัตรเอทีเอ็มข้างต้น ผู้ถอนเงินต้องมีข้อมูลระบุตัวตนว่าเป็นเจ้าของบัญชีตัวจริง ได้แก่ บัตรเอทีเอ็ม และรหัสประจำตัว 4 หลักและยังต้องระบุข้อมูลให้ครบถ้วนว่าต้องการเบิกถอนจากบัญชีใดเป็นจำนวนเงินเท่าใด เป็นต้น
- กำหนดวิธีการประมวลผล (Process Specification) ต้องทราบวิธีการประมวลผล หรือวิธีคิดให้ได้ผลลัพธ์ตามต้องการ
- การเลือกเครื่องมือและออกแบบขั้นตอนวิธี
เป็นการคิดค้นกระบวนการต่าง ๆ ที่เป็นลำดับขั้นตอน ซึ่งต้องอาศัยประสบการณ์และความรู้ของผู้แก้ปัญหา โดยอาจนำวิธีที่เคยแก้ปัญหา หรือค้นหาวิธีการอื่นแล้วนำมาประยุกต์เข้ากับปัญหาที่กำลังแก้ไข เครื่องมือที่ใช้ในการวางแผนแก้ไขปัญหาสำหรับการพัฒนาโปรแกรม อาจเลือกใช้รหัสลำลอง หรือผังงาน โดยวิธีการแก้ปัญหาแบบนี้ เรียกกว่า “ขั้นตอนวิธีหรืออัลกอริทึม (algorithm)”
สำหรับปัญหาที่มีขั้นตอนในการแก้ปัญหาอย่างซับซ้อน หรือต้องมีการแก้ปัญหาในลักษณะเดิมซ้ำอีกหลายครั้ง จำเป็นต้องใช้คอมพิวเตอร์เป็นอุปกรณ์ในการแก้ปัญหา โดยเขียนโปรแกรมเพื่อรับข้อมูลเข้าไปประมวลผล และยังต้องเลือกว่าจะใช้โปรแกรมคอมพิวเตอร์ภาษาใด ซึ่งขึ้นอยู่กับความคุ้นเคยในการใช้งานของผู้เขียนโปรแกรม และลักษณะเฉพาะของแต่ละภาษาที่เหมาะสมกับปัญหานั้น ๆ
ในการแก้ปัญหาโดยใช้คอมพิวเตอร์นั้น การออกแบบวิธีแก้ปัญหาอย่างเป็นขั้นตอนและง่ายต่อการทำความเข้าใจสำคัญมาก เพราะจะทำให้สามารถเขียนโปรแกรมจากขั้นตอนที่ได้ออกแบบไว้อย่างง่ายดาย เครื่องมือที่ใช้เพื่อการออกแบบขั้นตอนวิธี เช่น รหัสลำลอง (Pseudo code) ซึ่งเป็นการจำลองขั้นตอนวิธีแก้ปัญหา โดยการอธิบายด้วยคำพูดที่เข้าใจได้ง่ายเป็นขั้น ๆ หรือผังงาน (flowchart) ซึ่งเป็นการใช้สัญลักษณ์ในการแสดงรายละเอียดและลำดับของแต่ละขั้นตอนที่ใช้แก้ปัญหา ข้อดีอีกประการหนึ่งของการใช้เครื่องมือเหล่านี้ช่วยในการออกแบบวิธีแก้ปัญหาคือ จะทำให้สามารถตรวจสอบความถูกต้อง หาจุดผิดพลาด และแก้ไขขั้นตอนในการแก้ปัญหาที่ซับซ้อนได้รวดเร็ว นักเขียนโปรแกรมจึงควรฝึกฝนการใช้งานเครื่องมือเหล่านี้ให้เชี่ยวชาญ ตัวอย่างการเขียนรหัสลำลองและผังงาน
- การดำเนินการแก้ปัญหา
การดำเนินการแก้ปัญหา (Implementation) หลังจากที่ได้ออกแบบขั้นตอนวิธีเรียบร้อยแล้ว ขั้นตอนนี้เป็นขั้นตอนที่ต้องลงมือแก้ปัญหาโดยใช้เครื่องมือที่ได้เลือกไว้ หากการแก้ปัญหาดังกล่าวใช้คอมพิวเตอร์เข้ามาช่วยงาน ขั้นตอนนี้ก็เป็นการใช้โปรแกรมสำเร็จ หรือใช้ภาษาคอมพิวเตอร์เขียนโปรแกรมแก้ปัญหา ขั้นตอนนี้ต้องอาศัยความรู้เกี่ยวกับเครื่องมือที่เลือกใช้ซึ่งผู้แก้ปัญหาต้องศึกษาให้เข้าใจและเชี่ยวชาญ ในการดำเนินการอาจพบแนวทางที่ดีกว่าที่ออกแบบไว้ ผู้แก้ปัญหาก็สามารถปรับเปลี่ยนได้
- การตรวจสอบและปรับปรุง
การตรวจสอบและปรับปรุง (Refinement) หลังจากที่ลงมือแก้ปัญหาแล้ว ต้องตรวจสอบให้แน่ใจว่าวิธีการนี้ให้ผลลัพธ์ที่ถูกต้อง โดยผู้แก้ปัญหาต้องตรวจสอบว่าขั้นตอนวิธีที่สร้างขึ้นสอดคล้องกับรายละเอียดของปัญหา ซึ่งได้แก่ ข้อมูลเข้า และข้อมูลออก เพื่อให้มั่นใจว่าสามารถรองรับข้อมูลเข้าได้ในทุกกรณี อย่างถูกต้องและสมบูรณ์ ในขณะเดียวกันก็ต้องปรับปรุงวิธีการเพื่อให้การแก้ปัญหานี้ได้
ดังนั้น การแก้ปัญหา จึงเป็นกระบวนการที่เป็นระบบขั้นตอนในการแก้ปัญหาใดปัญหาหนึ่ง โดยใช้วิธีการดำเนินการแก้ปัญหาด้วยรูปแบบต่าง ๆ ด้วยกระบวนการแก้ปัญหา 4 ขั้นตอน ได้แก่ การวิเคราะห์และกำหนดรายละเอียดของปัญหา การเลือกเครื่องมือและออกแบบขั้นตอนวิธี การดำเนินการแก้ปัญหา การตรวจสอบและการปรับปรุง ซึ่งรายละเอียดได้กล่าวไปแล้วนั้น จะทำให้เราสามารถแก้ปัญหาได้อย่างเป็นระบบ ตามขั้นตอนวิธีและได้ผลลัพธ์ที่ดีที่สุด
แหล่งที่มา
ดนัยเทพ. (2562, 12 กันยายน). หลักการแก้ปัญหาด้วยคอมพิวเตอร์. สืบค้นเมื่อ 12 กันยายน 2562. จาก https://danaithep.wordpress.com/2012/07/23/บทที่-6-หลักการแก้ปัญหาด-2.
ปรีดาภรณ์ ไชยแสง. แนวคิดเชิงคำนวณ. สืบค้นเมื่อ 12 สิงหาคม 2562. จาก https://sites.google.com/a/kjn.ac.th/withyakar-khanwn/kh-naewkhid-cheing-khanwn
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). เทคโนโลยี (วิทยาการคำนวณ). สำนักพิมพ์จุฬาลงกรณ์ : กรุงเทพมหานคร.
กลับไปที่เนื้อหา
การเขียนรหัสลำลองและการเขียนผังงาน
เป็นการคิดค้นกระบวนการต่าง ๆ ที่เป็นลำดับขั้นตอน ซึ่งต้องอาศัยประสบการณ์และความรู้ของผู้แก้ปัญหา โดยอาจนำวิธีที่เคยแก้ปัญหา หรือค้นหาวิธีการอื่นแล้วนำมาประยุกต์เข้ากับปัญหาที่กำลังแก้ไข เครื่องมือที่ใช้ในการวางแผนแก้ไขปัญหาสำหรับการพัฒนาโปรแกรม อาจเลือกใช้รหัสลำลอง หรือผังงาน โดยวิธีการแก้ปัญหาแบบนี้ เรียกว่า ขั้นตอนวิธีหรืออัลกอริทึม โดยเฉพาะรหัสลำลองซึ่งเป็นเครื่องมือหนึ่งที่ช่วยให้ผู้แก้ปัญหาสามารถแก้ปัญหาได้สำเร็จ
รหัสลำลอง
รหัสลำลอง (Pseudo code) เป็นคำบรรยายที่เขียนแสดงขั้นตอนวิธี (algorithm) ของการเขียนโปรแกรม โดยใช้ภาษาที่กะทัดรัด สื่อสารกับโปรแกรมเมอร์ผู้เขียนโปรแกรม โดยอาจใช้ภาษาที่ใช้ทั่วไปและอาจมีภาษาที่ใช้ในการเขียนโปรแกรมประกอบ แต่ไม่มีมาตรฐานแน่นอนในการเขียนรหัสลำลอง และไม่สามารถนำไปทำงานบนคอมพิวเตอร์โดยตรงเพราะไม่ใช่คำสั่งในภาษาคอมพิวเตอร์ และไม่ขึ้นกับภาษาคอมพิวเตอร์ภาษาใดภาษาหนึ่ง
หลักเกณฑ์การเขียนรหัสลำลอง
มีการสรุปหลักเกณฑ์ ในการเขียนรหัสลำลองดังนี้
- ถ้อยคำหรือประโยคคำสั่ง (statement) ให้เขียนอยู่ในรูปแบบของภาษาอังกฤษอย่างง่าย
- ในหนึ่งบรรทัด ให้เขียนประโยคคำสั่งเพียงคำสั่งเดียว
- ควรใช้ย่อหน้าให้เป็นประโยชน์เพื่อแยกคำเฉพาะ (Keywords) ได้อย่างชัดเจน รวมถึงจัดโครงสร้างการควบคุมให้เป็นสัดส่วน ซึ่งการกระทำดังกล่าวจะทำให้อ่านง่าย
- แต่ละประโยคคำสั่งให้เขียนลำดับจากบนลงล่างโดยมีเพียงทางเข้าทางเดียวและมีทางออกทางเดียวเท่านั้น
- กลุ่มของประโยคคำสั่งต่าง ๆ อาจจัดรวมกลุ่มเข้าด้วยกันในรูปแบบของโมดูล แต่ต้องกำหนดชื่อโมดูลเหล่านั้นด้วย เพื่อให้สามารถเรียกใช้โมดูลเหล่านั้นได้
ตัวอย่างการเขียนรหัสลำลอง (Pseudo Code)
อัลกอริทีม (Algorithm)Algorithm การหาพื้นที่สามเหลี่ยม Pseudocodes Algorithm triangle
เริ่มต้น START
รับค่าความยาวของฐานมาเก็บในตัวแปร x READ X
รับค่ความยาวของสูงมาเก็บในตัวแปร Y READ Y
คำนวณหาพื้นที่ Compute ARRAY =(X"Y)/2
แสดงผลพื้นที่ Print ARRAY
จบ END
ประโยชน์ของการเขียนรหัสลำลอง
- เป็นเครื่องมือในการกำหนดโครงร่างกระบวนการทำงานของการเขียนโปรแกรมแต่ละโปรแกรม
- เป็นต้นแบบในการทบทวน ปรับปรุงแก้ไข และพัฒนาโปรแกรมของโปรแกรมเมอร์ และนักวิเคราะห์ระบบ
- เป็นตัวกำหนดงานเขียนโปรแกรม เพื่อให้โปรแกรมเมอร์นำไปพัฒนาเป็นโปรแกรมคอมพิวเตอร์ เพื่อสั่งให้ คอมพิวเตอร์ทำงานตามกระบวนการที่ได้จำลองกระบวนการจริงไว้ในรหัสลำลอง
รหัสลำลองจึงมีความสำคัญต่อการแก้ปัญหาเป็นตัวแทนของอัลกอริทึม โดยมีถ้อยคำหรือประโยคคำสั่งที่เขียนอยู่ในรูปแบบของภาษาอังกฤษที่ไม่ขึ้นกับภาษาคอมพิวเตอร์ภาษาใดภาษาหนึ่ง โดยการเขียนรหัสลำลองจะต้องคำนึงถึงหลักเกณฑ์ของการเขียนรหัสลำลองคำสั่งให้เขียนลำดับจากบนลงล่างและมีเพียงทางเข้าทางเดียวและมีทางออกทางเดียว รหัสลำลองจึงเป็นเครื่องมือในการกำหนดโครงร่างกระบวนการทำงานเป็นตัวกำหนดงานเขียนโปรแกรมเพื่อการพัฒนาโปรแกรมต่อไป
การเขียนผังงาน
ความหมายของการเขียนผังงาน
ผังงาน (Flowchart) คือ รูปภาพ (Image) หรือสัญลักษณ์(Symbol) ที่ใช้เขียนแทนขั้นตอน คำอธิบาย ข้อความหรือคำพูด ที่ใช้ในอัลกอริทึม (Algorithm) เพราะการนำเสนอขั้นตอนของงานให้เข้าใจตรงกัน ระหว่างผู้เกี่ยวข้อง ด้วยคำพูด หรือ ข้อความ ทำได้ยากกว่าเมื่อใช้รูปภาพ หรือสัญลักษณ์
ประเภทของผังงาน
ในการเขียนผังงานนั้นสามารถจำแนกแบบของผังงานออกเป็น 2 แบบใหญ่ ๆ คือ
1. ผังงานระบบ (System Flowchart) หรือผังงานในระดับกว้าง ซึ่งจะเป็นการแสดงขั้นตอนการทำงานของระบบทั้งหมด ผังงานระบบมักจะมีลักษณะย่นย่อ รวบรัด และแสดงเฉพาะตัวงานที่จะต้องทำในระบบเท่านั้น ไม่มุ่งเน้นรายละเอียดในการปฏิบัติ ไม่ได้แสดงว่างานนั้นจะทำอย่างไร ความสำคัญของผังงานระบบอยู่ที่การแสดงความสัมพันธ์ระหว่างงานต่าง ๆ ในระบบว่ามีความสัมพันธ์กันอย่างไร ตั้งแต่เรื่องของวัสดุอุปกรณ์ บุคลากร และหน่วยงานที่เกี่ยวข้อง
2. ผังงานโปรแกรม (Program Flowchart) หรือผังงานระดับละเอียด เป็นภาพแผนผังที่แสดงลำดับขั้นตอนในการทำงานของโปรแกรม ซึ่งจะแยกย่อยมาจากผังงานระบบ คือในแต่ละขั้นตอนจะแสดงการทำงานแต่ละคำสั่งโดยละเอียด ใส่วิธีการ และจัดลำดับขั้นตอนของโปรแกรม สำหรับโปรแกรมนั้น ๆ ตั้งแต่เริ่มต้นจากการรับข้อมูล การประมวลผล และไปจนถึงการแสดงผลลัพธ์ที่ได้จากการประมวลผลที่ผู้เขียนโปรแกรมกำลังทำงานอยู่ ไม่ได้แสดงความสัมพันธ์ระหว่างโปรแกรมนั้นกับโปรแกรมอื่น ๆ
สัญลักษณ์ผังงานโปรแกรม ( Program Flowchart )
การเขียนผังโปรแกรมจะประกอบไปด้วยการใช้สัญลักษณ์มาตรฐานต่าง ๆ ที่เรียกว่า สัญลักษณ์ ANSI ( American National Standards Institute ) ในการสร้างผังงาน ดังตัวอย่างที่แสดงในรูปต่อไปนี้
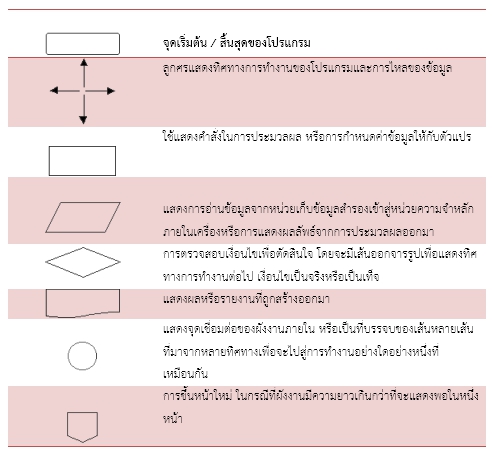
ภาพที่ 1 สัญลักษณ์ ANSI
ที่มา ฉัตรพงศ์ ชูแสงนิล
ลักษณะโครงสร้างของผังงาน
ผังงานทั่วไปจะประกอบด้วยโครงสร้างพื้นฐาน 3 รูปแบบต่อไปนี้คือ
1. โครงสร้างแบบเป็นลำดับ (Sequence structure)
2. โครงสร้างแบบมีการเลือก (Selection structure)
3. โครงสร้างแบบทำซ้ำ (Iteration structure)
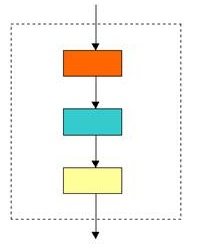
โครงสร้างแบบเป็นลำดับ (Sequence Structure)
เป็นโครงสร้างพื้นฐานของผังงาน และเป็นลักษณะขั้นตอนการทำงานที่พบมากที่สุด คือทำงานทีละขั้นตอนลำดับ
ภาพที่ 2 โครงสร้างแบบเป็นลำดับ
ที่มา https://kropomprograming.files.wordpress.com › flowchartandprogram, kropomprograming
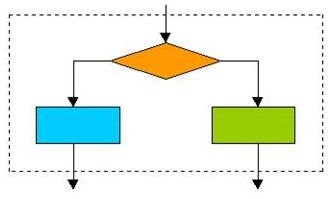
โครงสร้างแบบมีตัวเลือก (Selection Structure)
ภาพที่ 3 โครงสร้างแบบมีตัวเลือก
ที่มา https://kropomprograming.files.wordpress.com › flowchartandprogram, kropomprograming
โครงสร้างการทำงานแบบมีการเลือกมีรูปแบบที่ซับซ้อนกว่าโครงสร้างแบบเป็นลำดับรูปแบบที่ง่ายที่สุดของโครงสร้างแบบนี้คือ การเลือกแบบมีทางออก 2 ทาง ในการเลือกแบบมีทางออก 2 ทาง นี้จะมีทางออกจากสัญลักษณ์การตัดสินใจเพียง 2 ทาง คือ ใช่หรือไม่ใช่ เท่านั้น
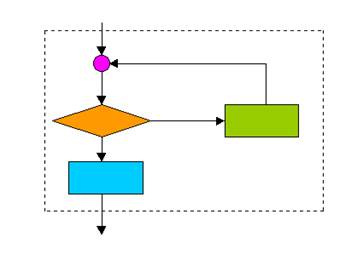
โครงสร้างแบบทำซ้ำ (Iteration Structure)
โครงสร้างการทำงานแบบทำซ้ำ จะทำงานแบบเดียวกันซ้ำไปเรื่อย ๆ ในขณะที่ยังเป็นไปตามเงื่อนไขหรือเงื่อนไขเป็นจริง จนกระทั่งเงื่อนไขเป็นเท็จจึงทำงานอื่นต่อไป
ภาพที่ 4 โครงสร้างแบบทำซ้ำ
ที่มา https://kropomprograming.files.wordpress.com › flowchartandprogram, kropomprograming
ประโยชน์ของผังงาน
ผังงานเป็นเครื่องมือที่ช่วยให้ลำดับขั้นตอนของโปรแกรมง่ายขึ้น จึงนิยมเขียนผังงานประกอบการเขียนโปรแกรม ด้วยเหตุผลดังนี้
1. การใช้ผังงานเป็นรูปแบบที่ไม่ขึ้นอยู่กับภาษาคอมพิวเตอร์ภาษาใดภาษาหนึ่ง ทำให้เรียนรู้และทำความเข้าใจได้ง่าย
2. ผังงานช่วยลำดับเป็นขั้นเป็นตอน เน้นสื่อความหมายด้วยภาพทำให้ง่ายต่อการทำความเข้าใจ แตกต่างจากการใช้ข้อความหรือคำพูดอาจจะสื่อความหมายผิดไปได้
3. เมื่อเกิดข้อผิดพลาดในขั้นตอนการเขียนโปรแกรมจะช่วยให้ตรวจสอบความถูกต้องของลำดับขั้นตอน และแก้ไขโปรแกรมได้ง่าย
4. ผังงานช่วยทำให้ผู้ที่มาทำต่อหรือศึกษาต่อทำความเข้าใจการทำงานของโปรแกรมได้อย่างง่าย สะดวก และรวดเร็วมากขึ้น
ดังนั้นผังงานจึงเป็นแผนภาพแสดงลำดับขั้นตอนการทำงานของอัลกอริทึม เป็นเครื่องมือที่ใช้การรวบรวมจัดลำดับความคิด เพื่อให้เห็นขั้นตอนการทำงานที่ชัดเจนและใช้วางแผนการทำงานขั้นแรก โดยสัญลักษณ์ Flowchart แสดงถึงการทำงานลักษณะต่าง ๆ เชื่อมต่อกัน โดยแบ่งประเภทของผังงานออกเป็น 2 แบบใหญ่ ๆ ได้แก่ ผังงานระบบ และผังงานโปรแกรม สัญลักษณ์ผังงานโปรแกรมโดยใช้สัญลักษณ์ ANSI โดยลักษณะโครงสร้างของผังงานจะประกอบด้วยโครงสร้างพื้นฐาน 3 รูปแบบ ได้แก่โครงสร้างแบบเป็นลำดับ โครงสร้างแบบมีการเลือก โครงสร้างแบบทำซ้ำ ซึ่งจะช่วยให้ลำดับรายละเอียดของคำสั่ง เป็นภาพแผนผังที่แสดงลำดับขั้นตอนในการทำงานของโปรแกรมได้
แหล่งที่มา
เจษฎา ก้องสาคร. (2562, 12 กันยายน). การเขียนผังงาน. สืบค้นเมื่อ 12 กันยายน 2562. จาก https://www.cmarea3.go.th/2562/การเขียนผังงาน-flowchart/
นิรุธ อำนวยศิลป์ (2548.) โครงสร้างข้อมูล : การเขียนโปรแกรมและการประยุกต์. ดวงกมลสมัย : กรุงเทพฯ.
สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2562). เทคโนโลยี (วิทยาการคำนวณ). สำนักพิมพ์จุฬาลงกรณ์ : กรุงเทพมหานคร.
โอภาส เอี่ยมสิริวงศ์. (2549.). โครงสร้างข้อมูลเพื่อการออกแบบโปรแกรมคอมพิวเตอร์. ซีเอ็ดยูเคชั่น : กรุงเทพฯ.
กลับไปที่เนื้อหา