คุณผู้อ่านที่ไม่ได้เชี่ยวชาญเรื่องดาราศาสตร์ เคยสงสัยกันไหมว่านักดาราศาสตร์รู้ได้อย่างไรว่าโลกของเรามีขนาดเท่าไร ดวงอาทิตย์อยู่ห่างจากโลกเท่าไร หรือแม้กระทั่งสามารถบอกได้ด้วยว่าดวงดาวที่อยู่ไกลแสนไกลมองเห็นเป็นเพียงจุดสว่างนั้นอยู่ห่างจากโลกของเราเท่าไร พวกเขาใช้อะไรวัด (ที่แน่ ๆ คงไม่ได้ใช้ไม้เมตร หรือสายวัด) และพวกเราอีกหลาย ๆ คนก็คงเคยสับสนกับคำว่า "ปีแสง" ว่าตกลงมันคือความเร็ว อัตราเร็ว หรือ ระยะทาง หรืออะไรกันแน่ และมีค่าเท่าไร? แม้จะฟังดูเป็นคำถามง่าย ๆ แต่ก็คงต้องใช้เวลาคิดหาคำตอบอยู่เหมือนกัน

ภาพ 1 ดาว "พร็อกซิมา เซนทอรี" (Proxima Centauri) ภาพจาก NASA/ ESA
(ที่มา: http://www.space.com/23475-proxima-centauri-hubble-telescope-photo.html)

1. ปัญหาในการใช้หน่วยกิโลเมตร

            หน่วยกิโลเมตร (kilometer ตัวย่อ km) หรือในบางประเทศนิยมใช้หน่วยไมล์ (mile ตัวย่อ mi) เป็นหน่วยที่ใช้วัดระยะทางไกล ๆ เช่น ระหว่างประเทศ เมือง หรือสถานที่ต่าง ๆ และยังเป็นหน่วยที่ใช้วัดระยะทางเฉลี่ยระหว่างโลกกับดวงอาทิตย์ซึ่งมีค่าประมาณ 150,000,000 กิโลเมตร (หนึ่งร้อยห้าสิบล้านกิโลเมตร) ได้ด้วย แต่ดวงดาวอื่น ๆ ที่อยู่ไกลออกไปจากโลกมากกว่าดวงอาทิตย์การใช้หน่วยกิโลเมตรเพื่อบอกระยะทางระหว่างโลกกับดวงดาวต่าง ๆ นั้นแม้ว่าจะใช้ได้แต่ก็ไม่เหมาะสมตัวอย่างเช่น ดาว "พร็อกชิมา เซนทอรี" (Proxima Centauri) ซึ่งเป็นดาวฤกษ์ที่อยู่ใกล้ระบบสุริยะของเรามากที่สุด อยู่ห่างจากโลก 41,512,200,000 000 กิโลเมตร จะเห็นูได้ว่าต้องเขียนตัวเลขยาวเหยียดหากเราใช้หน่วยกิโลเมตร ดังนั้นเพื่อแก้ปัญหานี้ นักวิทยาศาสตร์จึงนำหน่วย "ปีแสง" มาใช้ในการบอกระยะทางที่อยู่ไกลมาก ๆ แทน แล้วปีแสงคืออะไร ?

2. ปีแสง คืออะไร

            ปีแสง (light year ตัวย่อ ly) คือ ระยะทางที่แสงเดินทางในหนึ่งปี ซึ่งมีวิธีคิดดังนี้คือ เนื่องจากแสงมีอัตราเร็วในการเคลื่อนที่ในสุญญากาศประมาณ  3x10⁸ เมตร/วินาที ดังนั้นเราจะสามารถคำนวณได้ว่า ใน 1 ปีแสงจะเคลื่อนที่ (หรือเดินทาง) ได้เป็นระยะทางเท่าไร โดยการเทียบสัดส่วน (บางคนเรียกว่า เทียบบัญญัติตรยางศ์) ว่า 1 วินาที่ แสงเดินทางได้ 3x10⁸ เมตร ดังนั้น ใน 1 ปี (มีกี่วินาที หาให้ได้ก่อน) แสงจะเดินทางได้กี่เมตร

            จะเห็นได้ว่าเมื่อเราเขียนบอกระยะทางในหน่วยปีแสงจะใช้พื้นที่น้อยกว่าการเขียนในหน่วยกิโลเมตรมาก ด้วยเหตุนี้ นักวิทยาศาสตร์จึงมักบอกระยะทางจากโลกถึงดวงดาวต่าง ๆ ในหน่วยปีแสงมากกว่าหน่วยกิโลเมตร นอกจากนี้ยังให้ความรู้สึกได้ว่าแสงจากดาวเดินทางเป็นปีกว่าจะมาถึงโลก

3. วิธีวัดระยะทางแบบโดยตรงกับโดยอ้อม

            การวัดระยะทางสามารถทำได้ทั้งโดยตรงและโดยอ้อมซึ่งเราคุ้นเคยกับการวัดระยะทางแบบโดยตรงอยู่แล้ว คือ ใช้เครื่องมือวัดต่าง ๆ วัดระยะทางจากจุดหนึ่งถึงอีกจุดหนึ่งที่ต้องการทราบ ส่วนวิธีวัดระยะทางโดยอ้อมนั้นเราไม่จำเป็นต้องนำเครื่องมือวัดไปวัดระยะทาง แต่เราจะใช้หลักการของสามเหลี่ยมในการหาระยะทางแทน ซึ่งทำได้ดังนี้

วัสดุ-อุปกรณ์

1. ครึ่งวงกลมวัดมุม (หรือไม้โปรแทรกเตอร์)
2. ไม้เมตร
3. กระดาษการ์ด 3 แผ่น
4. ปากกาเคมี
5. เทปกาวใส
6. โต๊ะ

วิธีทำ

            1. วางโต๊ะไว้ใกล้กับผนังห้อง โดยให้ด้านยาวของโต๊ะขนานไปกับผนังห้อง นำกระดาษการ์ด 2 แผ่น วางบนโต๊ะโดยให้ขอบนอกของกระดาษอยู่ห่างกัน  100 เชนติเมตร แล้วยึดกระดาษการ์ดทั้งสองให้ติดกับโต๊ะด้วยเทปกาวใส

            2. ใช้ปากกาเคมีเขียนเครื่องหมายกากบาทขนาดใหญ่บนกระดาษการ์ดอีกแผ่น แล้วนำกระดาษนี้ไปติดที่ผนังห้องให้สูงระดับเดียวกับหน้าโต๊ะ (ดูภาพ 2)

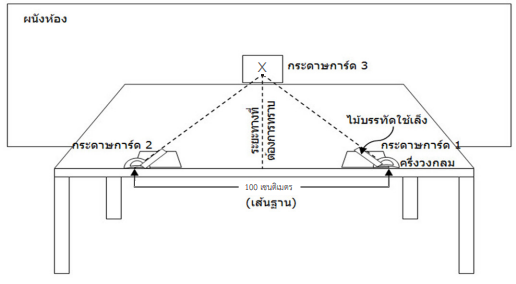
ภาพ 2 วิธีวัดระยะทางแบบโดยอ้อม

            3. นำครึ่งวงกลมวัดมุมวางบนกระดาษการ์ดโดยให้จุดกลางของครึ่งวงกลมอยู่ตรงมุมกระดาษการ์ดพอดี ให้ผู้สังเกตมองจุด X โดยดวงตาอยู่ระดับเดียวกับหน้าโต๊ะ โด้ยเริ่มมองจากทีละฝั่ง (อาจเริ่มจากฝั่งกระดาษการ์ด 1) ใช้ไม้บรรทัดเล็งระยะไปที่จุด X  แล้วให้เพื่อนช่วยอ่านค่ามุมที่เกิดจากเส้นฐานกับมุมที่ไม้บรรทัดเล็งไปที่จุด X ที่วัดได้จากครึ่งวงกลม บันทึกค่าไว้

            4. ทำเช่นเดียวกับข้อ 3. แต่เปลี่ยนเป็นมองจุด X จากตำแหน่งกระดาษการ์ด 2 ทำการวัดมุม แล้วบันทึกค่าไว้

            5. คำนวณหาระยะทางระหว่างจุดกึ่งกลางของเส้นฐานกับจุด X โดยวาดสามเหลี่ยมที่ได้จากการวัดเป็นสามเหลี่ยมย่อส่วนล่งในกระดาษทด (อาจกำหนดให้ 10 เชนติเมตร ในกระดาษทดของเราเท่ากับ 100 เชนติเมตร ในของจริง) นำครึ่งวงกลมมาวาดมุมให้เท่ากับที่วัดได้ลงที่ปลายเส้นฐานในกระดาษทด แล้วลากเส้นต่อทั้งสองด้านให้บรรจบกันจนเกิดเป็นสามเหลี่ยม ที่จุดปลายของสามเหลี่ยมคือตำแหน่งของ X แล้ววัดระยะทางตั้งแต่จุด X นี้จนถึงจุดกึ่งกลางของเส้นฐาน บันทึกค่าไว้ และคำนวณกลับไปเป็นระยะทางจริงของจุด X กับจุดกึ่งกลางที่ทำการทดลองบนโต๊ะ โดยการนำ 10 ไปคูณกับระยะทางที่วัดได้ในสามเหลี่ยมภาพ 3 หรือคำนวณส่วนสูงของสามเหลี่ยมจากความสูง = 5 tan q เชนติเมตร

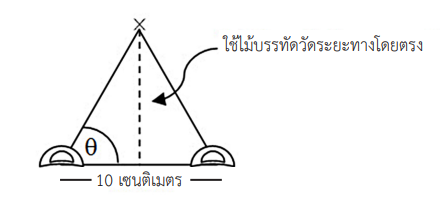
ภาพ 3 วิธีหาระยะทางในกระดาษทด

            6. ทดลองวัดระยะทางจริงจากจุด X บนผนังห้องมาถึงจุดกึ่งกลางของเส้นฐานที่วาดไว้บนโต๊ะ เทียบกับระยะทางที่ได้จากการคำนวณว่าใกล้เคียงกันหรือไม่ (ควรได้ค่าใกล้เคียงกัน)

4. วิธีวัดระยะทางจากโลกถึงดวงดาว

            เราสามารถใช้หลักการของสามเหลี่ยมข้างต้น มาใช้ในการหาระยะทางจากโลกถึงดวงดาวได้ นั่นคือ ลากเส้นฐานและวัดมุมที่เกิดจากเส้นฐานกับเส้นที่มองเห็นวัตถุ ดังภาพ 4

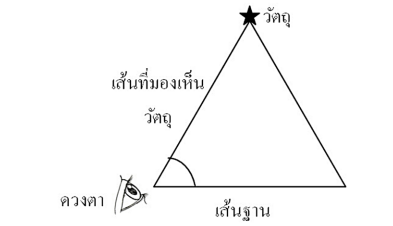
ภาพ 4 หลักการสามเหลี่ยมที่ประยุกต์ใช้ในการหาระยะทางจากโลกถึงดวงดาว

            สำหรับเส้นฐานที่ยาวที่สุดที่อยู่บนโลกมีค่า 12,742 กิโลเมตร (เส้นผ่านศูนย์กลางของโลกนั่นเอง) แต่เนื่องจากระยะทางดังกล่าวมีคำาน้อยมากแม้ว่าเทียบกับระยะทางจากโลกถึงดาวที่ใกล้โลกที่สุด ซึ่งหมายความว่าเส้นฐานใด ๆ ก็ตามบนโลกนั้นสั้นมาก!!! ด้วยเหตุนี้ เส้นการมองเห็นดวงดาวเมื่อผู้สังเกตอยู่ที่ตำแหน่งต่าง ๆ กันบนโลกจึงเป็นเส้นที่ขนานกัน ดังภาพ 5

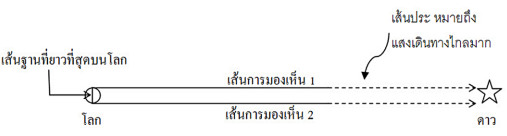
ภาพ 5 ภาพวาดแสดงเส้นการมองเห็นสองเส้นจากโลกจะขนานกัน
หมายเหตุ: ยกเว้นดาวที่อยู่ใกล้ ได้แก่ ดวงอาทิตย์ และดวงจันทร์ เป็นต้น

            ไม่ว่าจะสร้างเส้นฐานใด ๆ บนโลก เส้นการมองเห็นดวงดาวจากแต่ละด้านของสามเหลี่ยมก็เป็นเส้นที่ยาวและแคบมากเสมอและมุมที่ฐานของสามเหลี่ยมแต่ละด้านดูเหมือนจะเป็นมุมเกือบ 90 องศา ดังนั้นในการหาระยะทางจากโลกถึงดวงดาวนักดาราศาสตร์จึงใช้การถ่ายภาพและสร้างเส้นฐานที่ยาวกว่าเส้นฐานบนโลกมาก ๆ ขึ้นมา

            นักดาราศาสตร์ทำการบันทึกเส้นการมองเห็นดวงดาวที่อยู่ใกล้โลกจากตำแหน่งหนึ่งบนโลก จากนั้น เมื่อเวลาผ่านไป 6 เดือน จึงทำการสังเกตดาวดวงเดิมอีกครั้งจากตำแหน่งเดิมบนโลก ทำไมต้อง 6 เดือน? นั่นเป็นเพราะโลกของเราจะโคจรไปอยู่อีกฝั่งหนึ่งของดวงอาทิตย์พอดีนั่นเอง

            ระยะทางเฉลี่ยระหว่างโลกกับดวงอาทิตย์มีค่าประมาณ 150 ล้านกิโลเมตร นักดาราศาสตร์จึงใช้ความยาวเส้นฐานเป็นสองเท่าของระยะทางดังกล่าว หรือประมาณ 300 ล้านกิโลเมตร นั่นเองด้วยเส้นฐานที่ยาวมากขนาดนี้จึงทำให้นักดาราศาสตร์สามารถวัดมุมระหูว่างเส้นฐานกับเส้นการมองเห็นดาวได้ (ดูภาพ 6) และจากนั้นนักดาราศาสตร์ก็จะสามารถคำนวณหาระยะทางจากโลกถึงดวงดาวต่อไปได้โดยใช้หลักการของสามเหลี่ยมนี้เป็นพื้นฐาน

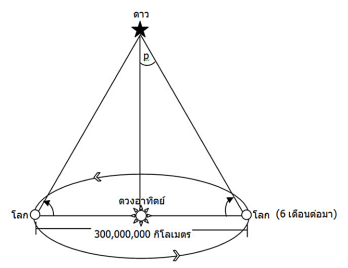
ภาพ 6 ภาพวาดแสดงการวัดระยะทางจากโลกถึงดวงดาวโดยใช้หลักการสามเหลี่ยมเป็นพื้นฐาน

            ระยะทางที่หาได้ในที่นี้จะเป็นระยะทางจากดวงอาทิตย์(กึ่งกลางของเส้นฐาน) ไปถึงดวงดาว แล้วระยะทางจากโลกถึงดวงดาวจะหาอย่างไร? ในความเป็นจริงแล้วระยะทางระหว่างดวงดาวกับดวงอาทิตย์กับระยะทางระหว่างดวงดาวดังกล่าวกับโลกแทบไม่แตกต่างกัน เพราะในสเกลที่ใหญ่ระดับเอกภพระยะทางจากดวงอาทิตย์ถึงโลก (150 ล้านกิโลเมตร) ถือเป็นระยะทางที่สั้นมาก ดังนั้นสามเหลี่ยมที่เกิดขึ้นดังภาพ 6 แท้จริงแล้วเป็นสามเหลี่ยมที่แคบมาก โดยเส้นฐานยาว 1 หน่วย ระยะของดวงดาวจะเป็นหลายแสนหลายล้ำนเท่าของฐาน จึงสรุปได้ว่าระยะทางจากโลกถึงดวงดาวก็มีระยะทางเท่า ๆ กับระยะทางจากดวงอาทิตย์ถึงดาวดวงนั้นด้วย

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Rand, M. & Company. (1971). Measuring distances indirectly. Interaction of Earth & Time, 102-105.Rand, M. & Company. (1971). Measuring distances to stars. Interaction of Earth & Time, 365-367.

ผู้จัดการออนไลน์. (4 ตุลาคม 2550). เปิดโผ 10 ที่สุดในจักรวาล.สืบคันเมื่อ 21 กุมภาพันธ์ 2558, จาก http://www.electron.rmutphysics.com/science-news/index. php?option=com content&task=view&id=517&ltemid=4&limit=1&limitstart=2.