คณิตศาสตร์เป็นวิชาที่มีความเป็นเหตุและผล และมีหลักการทางความคิดอย่างเป็นระบบ เชื่อว่าผู้อ่านบทความนี้คงเคยได้ศึกษาวิชานี้ คงเคยได้ผ่านกระบวนการหนึ่งทางคณิตศาสตร์มาบ้าง นั่นคือ การพิสูจน์ทางคณิตศาสตร์นั่นเอง เคยสงสัยบ้างไหมว่า ทำไมเราต้องทำการพิสูจน์ การพิสูจน์มีข้อดีอย่างไร ซึ่งในบทความนี้คงไม่ได้แสดงถึงหลักการทางการพิสูจน์ แต่อยากให้เห็นถึงความสำคัญเพียงเท่านั้น

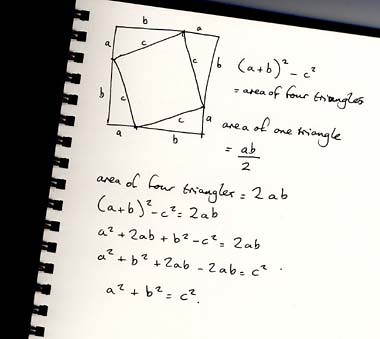
ภาพการพิสูจน์ทฤษฎีบทพีทาโกรัส
ที่มา https://www.flickr.com/photos/recurrence/34904701/

การพิสูจน์ทางคณิตศาสตร์

          การพิสูจน์ (Proof) มีความหมายที่มาจากภาษาละตินว่า  “ทดสอบ” เราทราบกันดีว่าในระบบคณิตศาสตร์นั้น  ทฤษฎีบท (theorems) คือประพจน์ที่ได้มีการพิสูจน์แล้วว่าเป็นจริง ซึ่งสามารถนำไปใช้ประโยชน์ในการหาคำตอบทางคณิตศาสตร์หรือนำไปใช้พิสูจน์ทฤษฎีบทอื่นต่อได้นั่นเอง

          การแสดงให้เห็นว่าข้อความหรือที่เราเรียกว่าประพจน์เป็นจริง เราจะต้องแสดงหรือพิสูจน์ให้เห็นว่าการพิสูจน์เป็นจริงทุกกรณี ก็เพราะว่าคณิตศาสตร์แต่ละอย่างจะเป็นการต่อยอดจากคณิตศาสตร์ตัวก่อนหน้า ถ้าเกิดว่าสิ่งที่เราพิสูจน์มามีความผิดพลาดจะทำให้สิ่งที่ต่อยอดมาจากสิ่งสิ่งนั้นผิดไปด้วยทั้งหมด

การพิสูจน์ทางคณิตศาสต์มีด้วยกันทั้งหมดประมาณ 4 รูปแบบ ดังนี้

1. การพิสูจน์โดยตรง (Direct proof)

2. การหาข้อขัดแย้ง (Proof by contradiction)

3. การแย้งสลับที่ (Contrapositive)

4. การพิสูจน์โดยใช้อุปนัยเชิงคณิตศาสตร์ (Mathematical induction)

        สิ่งสำคัญของการพิสูจน์ทางคณิตศาสตร์ ส่วนหนึ่งต้องเริ่มจากการเข้าใจธรรมชาติและความคิดรวบยอดเกี่ยวกับโครงสร้างของคณิตศาสตร์ ที่เคยได้นำเสนอไปในบทความก่อนหน้านี้ (คณิตศาสตร์มีโครงสร้างหรือเปล่า) การพิสูจน์ส่วนใหญ่จะมีการใช้ประโยชน์จากหลักการทางคณิตศาสตร์ในเรื่องของตรรกศาสตร์เข้ามาเกี่ยวข้องในการพิสูจน์ และมีการใช้ภาษาที่เกิดขึ้นตามธรรมชาติเพื่อการสื่อสารหรือ ภาษาธรรมชาติ (natural language) มาอธิบายรูปแบบหรือการดำเนินการนั้น ๆ

        ที่ผ่านมาส่วนใหญ่การพิสูจน์ทางคณิตศาสตร์จะสอดแทรกให้ผู้เรียนได้ทดลองพิสูจน์กันในระดับมัธยมศึกษา เช่น การพิสูจน์ในทางเรขาคณิต ในขณะเดียวกันเมื่อเราเรียนในระดับที่สูงขึ้น หรือเรียนในหลักสูตรเฉพาะทางที่มีการคำนวณเข้ามาเกี่ยวข้อง การอ่านบทนิยามและพิสูจน์ทฤษีบทให้เข้าใจในเนื้อหาได้อย่างลึกซึ้ง  ก็จะช่วยให้เราสามารถทำความเข้าใจในหลักการทางคณิตศาสตร์ที่มีเนื้อหาสูงขึ้นได้ไม่ยาก

        ที่กล่าวมาทั้งหมดนี้ จึงอยากจะฝากให้ผู้อ่านทุกท่าน พยายามทำความเข้าใจเกี่ยวกับโครงสร้างของคณิตศาสตร์และหลักการทางตรรกศาสตร์ซึ่งเป็นพื้นฐานกันไว้ให้มาก เพราะเป็นเครื่องมืออย่างหนึ่งที่จะทำให้เราสามารถศึกษาคณิตศาสตร์ได้อย่างถ่องแท้ จากการพิสูจน์ในทางคณิตศาสตร์ได้นั่นเอง

แหล่งที่มา

หลักการคณิตศาสตร์ (Mathematics Principle) MAP1401 สาขาวิชาคณิตศาสตร์ คณะครุศาสตร์ มหาวิทยาลัยราชภัฏสวนสุนันทา.  สืบค้นเมื่อวันที่ 15 มิถุนายน 2563. จาก www.eledu.ssru.ac.th/chouang_ut/pluginfile.php/17/block_html/content/บทที่%203%20การพิสุจน์.pdf

ธนพรรษ พฤกษะวัน. การศึกษาความสามารถและปัญหาในการพิสูจน์ทางคณิตศาสตร์ของนักศึกษาหลักสูตรศึกษาศาสตรบัณฑิต สาขาวิชาคณิตศาสตร์มหาวิทยาลัยสวนดุสิต.สืบค้นเมื่อวันที่ 15 มิถุนายน 2563. จาก https://so03.tci-thaijo.org/index.php/sduhs/article/download/186594/131104/

ผู้ช่วยศาสตราจารย์ ดร.ฉวีวรรณ รัตนประเสริฐ . วิธีการพิสูจน์ทางคณิตศาสตร์.สืบค้นเมื่อวันที่ 15 มิถุนายน2563. จาก https://so03.tci-thaijo.org/index.php/sduhs/article/download/186594/131104/