"จิตนิสัยทางคณิตศาสตร์ (Mathematical Habits of Mind) เป็นความเข้าใจคณิตศาสตร์ในรูปแบบที่คณิตศาสตร์เป็น จึงเปรียบเสมือนสะพานเชื่อมโยงความคิดและมุมมองระหว่างผู้ใช้และผู้เรียนคณิตศาสตร์กับผู้วิจัยคณิตศาสตร์ (นักคณิตศาสตร์ จิตนิสัยทางคณิตศาสตร์จึงเป็นสิ่งที่ทั้งนักวิชาการด้านคณิตศาสตร์และนักคณิตศาสตร์ให้ความสนใจที่จะใช้เป็นเครื่องมือสำหรับพัฒนาให้ผู้เรียนมีวิธีการคิดเยี่ยงนักคณิตศาสตร์ (think about mathematics the way mathematicians do)"

            หลายคนอาจมองว่าคณิตศาสตร์เป็นเพียงศาสตร์แห่งการคิดคำนวณที่เกี่ยวกับตัวเลข แต่นั่นไม่ใช่ความจริงทั้งหมด เพราะคณิตศาสตร์อื่น " อีกหลายสาขายังมีเนื้อหาที่ไม่ได้มุ่งเน้นการคำนวณเป็นสำคัญ เช่น ตรรกศาสตร์การพิสูจน์ ทฤษฎีกราฟ ฯลฯ ดังนั้นถ้าจะกล่าวให้ได้ความครอบคลุมผู้เขียนอยากจะใช้คำว่า "คณิตศาสตร์เป็นศาสตร์เกี่ยวกับระบบวิธีคิด" การเรียนคณิตศาสตร์จึงไม่ควรมุ่งเน้นแค่การเร่ งรัดนำนักเรียนไปให้ถึงคำตอบด้วยวิธีการสำเร็จรูป แต่ควรเปิดโอกาสให้ผู้เรียนได้ฝึกคิดใช้การเชื่อมโยงตรรกะ และกลยุทธ์การแก้ปัญหา (logical and heuristic connections) ระหว่างองค์ความรู้แต่ละเรื่อง เพื่อสร้างสิ่งที่มีคุณค่ายิ่งกว่าคำตอบ และนี่คือสิ่งที่เรียกว่า "จิตนิสัยทางคณิตศาสตร์ (Mathematical Habits of Mind)"

จิตนิสัยทางคณิตศาสตร์คืออะไร

            จิตนิสัยทางคณิตศาสตร์ เป็นคำที่ถูกนำมาใช้เป็นครั้งแรกโดย Cuoco, Goldenberg, and Mark (1996) ซึ่งได้เสนอว่า จิตนิสัยทางคณิตศาสตร์เป็นหลักการสำคัญของการจัดหลักสูตรคณิตศาสตร์ เพื่อให้นักเรียนระดับมัธยมศึกษาและวิทยาลัยได้ทำความเข้าใจคณิตศาสตร์ด้วยวิธีการคิดแบบนักคณิตศาสตร์จึงเป็นส่วนที่เติมเต็มช่องว่างระหว่างผู้สร้างกับผู้ใช้คณิตศาสตร์ แม้ปัจจุบันวงการอาจยังไม่มีนิยามที่ชัดเจนตายตัว แต่ Lim and Selden (2009) ได้อธิบายความหมายของจิตนิสัยทางคณิตศาสตร์อย่างง่ายๆ โดยใช้คำสำคัญ 2 คำ คือ "การคิด (hinking)" และ "ความเคยชินเป็นนิสัย (habituated)" ซึ่งเราสามารถปลูกฝังสมบัติสองสิ่งนี้แก่ผู้เรียนได้โดยอัตโนมัติ ขณะฝึกหัดโดยใช้โจทย์ปัญหาในชั้นเรียน เพียงแต่ครูต้องตั้งคำถามหรือจัดหาปัญหาที่เหมาะสมมาให้ผู้เรียนทำเพื่อกระตุ้นการคิด (Seeley. 2014)

            Harel (2008) ได้ให้ทรรศนะเกี่ยวกับจิตนิสัยในมุมมองเป็นวิธีคิดว่าคณิตศาสตร์ประกอบด้วย 2 สับเซต คือ 1 วิธีทำความเข้าใจได้แก่ นิยาม สัจพจน์ ทฤษฎีบท ข้อพิสูจน์ปัญหา และการหาคำตอบ และ 2) วิธีคิด (ways of thinking) เป็นเครื่องมือทางความคิดที่มีประโยชน์ต่อการสร้างสับเซตแรกและสิ่งที่ทำให้วิธีคิดแตกต่างจากเครื่องมือทำความเข้าใจก็คือ จิตนิสัยทางคณิตศาสตร์ ทั้งสองความหมายนี้ไม่สามารถจะแยกกันพัฒนาได้

            ขณะที่ Mason and Spence (1999) มีความเห็นว่าลักษณะที่เป็นความเคยชินจะต้องเป็นนิสัยที่รู้และปฏิบัติได้ทันที โดยแบ่งความรู้ออกเป็น 2 ประเภทคือ 1) รู้เนื้อหา (knowing-about) ประกอบด้วย การรู้ข้อเท็จจริง รู้กระบวนการและรู้เหตุผลเบื้องลึก และ 2) รู้จักใช้ (knowing-to) เป็นความรู้ฝั่งแน่นที่สามารถแสดงได้ตามบริบทหรือสถานการณ์ในทันทีที่ต้องการ ซึ่งความรู้ประเภทหลังนี้เป็นสิ่งที่มีความจำเป็นยิ่งกว่า

            นอกจากนี้ Costa and Kallick (2000) ได้อธิบายความหมายของคำว่า "จิตนิสัย" ว่าเป็นผลอันเกิดจากการคิดวิเคราะห์เพื่อแก้ปัญหาในสถานการณ์จริง และเกิดการเรียนรู้ที่จะนำไปสู่ผลลัพธ์หรือวิธีการแก้ปัญหาที่ดีกว่า ซึ่งหากนำมาพิจารณาร่วมกันแล้วอาจพอสรุปความหมายได้ว่า จิตนิสัยทางคณิตศาสตร์  เป็นการมองเห็นความสัมพันธ์ระหว่างเนื้อหาทางคณิตศาสตร์ต่าง ๆ และสามารถคิดเชื่อมโยงนำโครงสร้างความรู้ที่มีอยู่มาจัดการกับสถานการณ์หรือปัญหาที่พบเพื่อหาคำตอบได้อย่างมีประสิทธิภาพ โดยสามารถนำไปปฏิบัติได้อย่างสม่ำเสมอจนเกิดเป็นนิสัย

จิตนิสัยทางคณิตศาสตร์นั่นมีความสำคัญอย่างไร

            Tall ได้กล่าวถึงตัวอย่างความทรงพลังของการมีจิตนิสัยทางคณิตศาสตร์ไว้ดังนี้

            เด็กคนหนึ่งหาคำตอบของ 8+6 ด้วยการเปลี่ยนให้อยู่ในรูป 8+2+ 4 = 10+4 โดยแยก 6 เป็น 2+4 เพื่อที่จะได้นำ 2 ไปรวมกับ 8 ให้ครบ 10 แล้วเพิ่ม 4 เป็น 14

            หรือกรณีการอภิปรายเรื่องขั้นตอนการหารด้วย 7 เด็กคนหนึ่งอาจไม่ได้คิดถึงขั้นตอนการหาร แต่กลับนึกไปถึงจำนวนที่เกี่ยวข้องกัน เช่นเมื่อเพื่อนถามเขาว่า 121 หารด้วย 7 ลงตัวหรือไม่ เขาตอบได้ทันทีว่า "ไม่" เพราะ 121 คือ 11² นั่นคือสิ่งที่เกิดขึ้นในห้วงความคิดของเขาไม่เพียงแต่เป็นการจะแยกตัวประกอบเท่านั้น หากมองลึกลงไปถึงการแยกเป็นตัวประกอบที่ซ้ำจำนวนเดียวกันด้วย สำหรับการหาร 131 ด้วย 7 เขาได้ตอบว่า "หารไม่ลงตัว" เพราะ 131 คือ 140หักออกเสีย 9 แต่เขาจนมุมที่จำนวน 119 ซึ่งเขาไม่สามารถคิดด้วยวิธีอื่นใดได้นอกจากคิดตามขั้นตอนการหารด้วย 7 ตามปกติจะได้ผลลัพธ์เป็น 17 อย่างไรก็ตาม จิตคณิตศาสตร์ของเขาก็ยังไม่ยอมหยุดอยู่แค่นั้น เขายังมองเห็นความสัมพันธ์ใหม่ว่า 17 X 7 คือ 10X 7 รวมกับ 7X7 ซึ่งเท่ากับ 70+ 49 = 119 หรือมันคือ 20 คูณ 7 แล้วหักออกด้วย 3 คูณ 7 ซึ่งเท่ากับ 140 - 21 = 119 วิธีคิดเหล่านี้ทำให้เขารู้สึกมีความสุขได้อีกคำรบหนึ่ง เพราะจิตคณิตศาสตร์ของเขาได้เพิ่มแบบรูปของความสัมพันธ์ใหม่ โดยช้มโนทัศน์ที่เขาได้พัฒนาขึ้นมาเองสำหรับเลขจำนวน 7

            กระบวนการคิดเชิงจำนวนข้างต้นมีความซับซ้อนกว่าขั้นตอนการหาคำตอบธรรมดา เพราะมันสะท้อนให้เห็นการมีโครงสร้างความรู้ที่สอดคล้องกับโครงสร้างทางสมองในเรื่องความรู้สะสมและการเชื่อมโยงภายในโครงสร้างเหล่านั้น ตลอดจนวิธีการจัดการกับปัญหาต่าง ๆ ที่เกิดขึ้นในเวลาเดียวกัน โดยมุ่งไปสนใจสิ่งที่ต้องการได้

คุณลักษณะแบบใดที่เรียกว่ามีจิตนิสัยทางคณิตศาสตร์

            Cuoco, Goldenberg, and Mark (1996) ได้เสนอลักษณะเฉพาะของผู้ที่มีจิตนิสัยทางคณิตศาสตร์ไว้ 9 ประการ ได้แก่

1. สามารถเข้าใจกรณีทั่วไปได้โดยใช้กรณีตัวอย่างหลายกรณี โดยการนำหลักการใหญ่ที่มักเป็นนามธรรมเพื่อให้เห็นภาพและเข้าใจด้วยตัวอย่างที่เป็นรูปธรรม
2. คิดพิจารณาจากจุดเล็ก ๆ เพื่อนำไปสู่หลักการที่ยิ่งใหญ่ มีบ่อยครั้งที่ความรู้ทงคณิตศาสตร์ได้แตกสาขาการพัฒนาขึ้นมาใหม่จากการพยายามจะแก้ปัญหาธรรมดา ๆ ตัวอย่างเช่น จงหาผลคูณของจำนวนที่เกิดจากผลรวมของจำนวนกำลังสอง (square number) ที่สามารถเขียนให้อยู่ในรูปผลรวมของจำนวนกำลังสองที่แตกต่างจากจำนวนเดิม

            เช่น 13 = 3² + 2² และ 5 = 2² + 1² (ทั้ง 13 และ 5 ต่างเกิดจากผลบวกของจำนวนกำลังสอง) จะได้ว่า 65 = 13 X 5 = 16 + 49 = 4² + 7²

            แสดงว่า 65 ซึ่งเกิดจาก 13 คูณกับ 5 ก็สามารถเขียนให้อยู่ในรูปผลบวกของจำนวนกำลังสองได้ด้วยการที่เป็นเช่นนี้ก็เพราะหลักการทางเลขคณิตของจำนวนเต็มเกาส์ (Gaussian integers) ที่แสดงให้เห็นว่า

            (a + bi)(a - bi) = a + b. เมื่อ I คือรากที่สองของ -1 ดังนั้น จากจำนวนเต็ม 13 และ 5 เราสามารถเขียนได้ว่า 13 = (3 + 2i)(3 – 2i) และ 5 = (2 + i)(2 - i)

             จึงได้ว่า   13 X 5   = (3 + 2i(3 - 2i) X (2 + i)l(2 - i)
                                         = (3 + 2i) (2 + i) X (3 - 2i) (2 - i)
                                         = (4 +7i) X (4 -71)
                                         = 16 + 49

            การที่จะสร้างและประยุกต์ทฤษฎีและตัวอย่างเหล่านี้ได้ ผู้เรียนจำเป็นต้องอาศัยการตกตะกอนจากประสบการณ์ที่หลากหลาย จากการสังเกต เชื่อมโยง และทดลองเล่นสนุกกับเลขคณิตทั้งที่เป็นจำนวนเต็มสามัญ (ordinary integers) และจำนวนเชิงซ้อน (complex numbers) รวมถึงเห็นความคล้ายคลึงของสถานการณ์ที่ต่างกัน แต่ความสามารถเหล่านี้ใช่ว่าเด็กทุกคนจะคิดและทำได้เอง เขาจำเป็นต้องได้รับความช่วยเหลือในการเริ่มต้น

3. รู้จักใช้เครื่องมือทางคณิตศาสตร์ เพราะความรู้คณิตศาสตร์ที่ค้นพบวันนี้จะกลายเป็นเครื่องมือสำหรับการค้นคว้าต่อไปในอนาคต เครื่องมือทางคณิตศาสตร์ที่สำคัญได้แก่ ขั้นตอนวิธี (Algorithms) การแปรตาม (Dependences) และการส่ง (Mappings)
4. ใช้มุมมองที่หลากหลาย (use multiple points of view) เช่น ในการศึกษาระบบจำนวนเชิงซ้อน จำเป็นต้องอาศัยทั้งมุมมองแบบพืชคณิต (ความรู้เกี่ยวกับสมการ)การวิเคราะห์ (ความต่อเนื่องของฟังก็ชัน) และเรขาคณิต(รูปหลายเหลี่ยมปกติ) ประกอบกัน
5. ผสมผสานระหว่างวิธีการนิรนัยกับการทดลอง(mix deduction and experiment) การพิสูจน์ด้วยวิธีนิรนัย (deductive proo!) ยังเป็นเรื่องที่นักคณิตศาสตร์ศึกษาถกเถียงกันอยู่ว่ามีความจำเป็นหรือไม่ สำหรับการเรียนในโรงเรียนหรือเพิ่มเข้าไปเพียงเพื่อให้เนื้อหาน่าเชื่อถือยิ่งขึ้น เพราะแม้นักคณิตศาสตร์หลายคนจะเชื่อว่าองค์ความรู้คณิตศาสตร์เกิดจากการพิสูจน์และทุกอย่างที่เป็นจริงจะต้องสามารถพิสูจน์ได้ แต่บางครั้งองค์ความรู้ก็สามารถเกิดได้จากการทดลองโดยการสังเกตเห็นบางสิ่งบางอย่าง แล้วมีความสงสัยจนนำมาซึ่งการสรุปเป็นคำอธิบายได้ แต่อย่างน้อยการพิสูจน์และการสร้างคำอธิบายก็สามารถช่วยให้เกิดกระบวนการสืบเสาะหาความรู้ได้ 2 แนวทางคือ 1) ใช้วิธีการพิสูจน์ช่วยยืนยันผลลัพธ์ และ 2) ใช้การพิสูจน์เป็นเครื่องมือในการสร้างทฤษฎีบทใหม่
6. ส่งเสริมการใช้ภาษา (push the language) เพื่อสร้างคำอธิบาย เช่น นิยามการมีอยู่ของจำนวน 2⁰ ซึ่งในบางครั้งการพบข้อขัดแย้งก็อาจสามารถนำมาซึ่งการสร้างทฤษฎีบทใหม่ ๆ ได้
7. ร่วมกันใช้ปัญญาครุ่นคิด (use intellectual chants) ทั้งแบบร่างลงบนกระดาษและคิดในใจ ซึ่งครูสามารถส่งเสริมได้โดยใช้การสัมภาษณ์นักเรียนคนที่แก้ปัญหาได้สำเร็จโดยอาจขอให้อธิบายและเขียนวิธีการที่ใช้แก้ปัญหา
8. ใช้วิธีการทางเรขาคณิตในการแก้ปัญหา (geometric approaches to things) ความคิดแนวเรขาคณิตได้มีบทบาทสำคัญต่อคณิตศาสตร์ทุกสาขามาโดยตลอดมุมมองเชิงเรขาคณิตจะช่วยสร้างความเข้าใจที่ถูกต้องในการค้นพบใหม่ ๆ อาทิใช้ในการวิเคราะห์เชิงซ้อน (complex analysis)
9. ใช้วิธีการทางพีชคณิตในการแก้ปัญหา (algebraic approaches to things) อาทิ ใช้เป็นเครื่องมือคำนวณที่ดี ใช้แปลงให้อยู่ในสภาพนามธรรม ใช้เป็นขั้นตอนวิธี (use algorithms) ใช้แบ่งเป็นส่วนย่อยใช้ขยาย และใช้เป็นตัวแทน

จะปลูกฝังอย่างไรให้ผู้เรียนมีจิตคณิตศาสตร์

            Cuoco, Goldenberg, and Mark (1996) ได้เสนอแนะแนวทางการสร้างจิตนิสัยทางคณิตศาสตร์ว่าผู้เรียนควรได้รับการพัฒนาและส่งเสริม โดยสอดแทรกสิ่งต่อไปนี้ลงไปในบริบทหรือสถานการณ์ที่เหมาะสม

• ผู้เรียนควรได้ฝึกการเป็นผู้ค้นพบแบบแผน จะช่วยให้ผู้เรียนเกิดความภาคภูมิใจจากการได้ค้นพบ
• ผู้เรียนควรได้ฝึกเป็นนักทดลอง โดยการกระตุ้นให้มีความสงสัยใคร่รู้
• ผู้เรียนควรได้ฝึกเป็นนักอธิบายสื่อสาร ทั้งด้วยวิธีเขียนและอธิบายปากเปล่า
• ผู้เรียนควรเป็นเหมือนช่างบัดกรี ที่สามารถเชื่อมผสานแนวคิดต่าง ๆ ให้เข้ากันได้ด้วยดี
• ผู้เรียนควรได้ฝึกเป็นนักประดิษฐ์ ซึ่งอาจฝึกได้ทั้งแบบมีวัตถุประสงค์ที่มุ่งเน้นประโยชน์ หรือเพื่อความสนุกสนานด้วยวิธีเล่นเกม ขั้นตอนวิธีการอธิบายการทำงาน หรือแม้แต่สัจพจน์ที่ใช้ในโครงสร้างเชิงคณิตศาสตร์
• ผู้เรียนควรฝึกเป็นนักวาดภาพ โดยการแปลงข้อความปัญหาออกมาเป็นภาพจำลองจะช่วยให้
• ผู้เรียนมีแนวคิดหรือเห็นแนวทางวิธีจัดการกับปัญหาได้ เช่น การใช้แผนภาพแสดงพื้นที่อธิบายความคิดรวบยอดเกี่ยวกับผลคูณทวินาม (a + b)² = a² + 2ab + b² ดังรูป

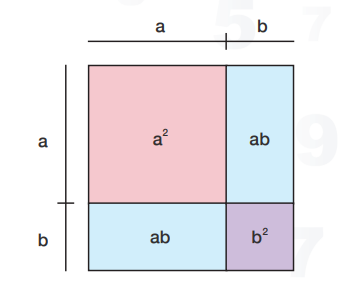
จากรูปแสดงให้เห็นว่า รูปสี่เหลี่ยมจัตุรัสรูปใหญ่ที่มีความยาวด้าน 2+6 หน่วย จะมีพื้นที่เท่ากับ (2+b)' ตารางหน่วย ซึ่งเกิดจากผลรวมของพื้นที่รูปสี่เหลี่ยมย่อยทั้ง 4 รูป จึงสรุปได้ว่า (a+ b)² = a² + ab + ab + b² = a² + 2ab + b² นั่นเอง

• ผู้เรียนควรฝึกเป็นนักคาดการณ์ การคาดการณ์ได้อย่างน่าเชื่อถืออาจจำเป็นต้องใช้เวลานานแต่ถือเป็นหัวใจสำคัญของการเรียนคณิตศาสตร์อย่างน้อยที่สุดผู้เรียนควรสามารถสร้างข้อความคาดการณ์จากข้อมูลที่มีอยู่ได้ (เช่น มองเห็นแบบรูปของจำนวน) เพราะข้อความคาดการณ์ที่สร้างขึ้นถ้าดีควรจะไปได้ไกลกว่าผลการทดลองขณะนั้น หรือสามารถพยากรณ์บางสิ่งบางอย่างได้
• ผู้เรียนควรฝึกการคาดเดา บ่อยครั้งที่การลองแทนค่าด้วยคำตอบที่เป็นไปได้ลงในโจทย์แล้วทำย้อนกลับ จะช่วยให้พบค่าประมาณที่ใกล้เคียงกับคำตอบที่แท้จริงได้ กระบวนการตรวจสอบคำตอบนี้มีส่วนช่วยให้ผู้เรียนมีความเข้าใจที่ลึกซึ้ง (insights) ยุทธวิธี (strategies) และแนวทาง (approaches)

            จะเห็นได้ว่า การปลูกฝังจิตนิสัยทางคณิตศาสตร์ให้แก่ผู้เรียนไม่ใช่สิ่งที่จะสอนให้ตระหนักรู้ได้ในช่วงเวลาอันสั้นหรือสอนแบบแยกส่วนจากเนื้อหาแต่ละเรื่องได้ แต่จำเป็นต้องผ่านการฝึกฝนอย่างต่อเนื่องและยาวนานโดยสอดแทรกอยู่ในกระบวนการคิดทางคณิตศาสตร์ของทุกเนื้อหาและทุกระดับชั้น จนผู้เรียนมีความแตกฉานในเนื้อหาพอที่จะสามารถเชื่อมโยงความรู้ได้เอง กล่าวสรุปง่าย ๆ คือ "ผู้เรียนต้องคิดจนติดเป็นนิสัย" การสอนจึงจะบรรลุผลได้อย่างแท้จริง

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Costa. A.. & Kallick, B. (2000). Habits of mind: A developmental series. Alexandria. VA: Association for Supervision and Curriculum Development.

Cuoco, A.. Goldenberg. E. P.. & Mark, J. (1996). Habits of mind: An organizing principle for a mathematics curriculum. Journal of Mathematical Behavior. 15 (4), 375-402.

Harel, G. (2008). What is mathematics? A pedagogical answer to a philosophical question. Current issues in the philosophy of mathematics from the perspective of mathematicians. Washington, DC: Mathematical American Association.

Lim, K. H., & Selden, A. (2009). Mathematical habits of mind. Proceedings of the Thirty-first Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Atlanta: Georgia State University.

Mason, J.. & Spence, M. (1999). Beyond mere knowledge of mathematics: The importance of knowing-to act in the moment. Educational Studies in Mathematics. 38. 135-161.

Seeley, C. L. (2014). Smarter Than We Think: More Messages About Math. USA: Scholastic Inc.

Tall, D. (2000). Biological Brain. Mathematical Mind & Computational Computers. Retrieved May 20. 2016. From http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot2000h-plenary-atcm2000.pdf.

ไพจิตร สดวกการ. (2553). จิตคณิตศาสตร์. สืบคั้นเมื่อ 12 พฤษภาคม 2559, จาก http:/www.krupai.net.