ถึงแม้ว่าลำดับของวิชาคณิตศาสตร์ (Mathematics) ในชื่อกลุ่มวิชาสะเต็มศึกษา (STEM) จะอยู่ในตำแหน่งรั้งท้าย แต่ก็ไม่ได้หมายความว่าวิชาคณิตศาสตร์มีความสำคัญน้อยกว่าวิชาอื่น ๆ เพราะจริง ๆ แล้ววิชาคณิตศาสตร์ถือเป็นรากฐานสำคัญสำหรับการเรียนรู้วิชาอื่น ๆ ในกลุ่มสะเต็มศึกษาไม่ว่าจะเป็นวิทยาศาสตร์(Science) เทคโนโลยี (Technology) หรือกระบวนการทางวิศวกรรม (Engineering) ซึ่งล้วนสามารถนำความรู้ทางคณิตศาสตร์มาประยุกต์ใช้ได้ทั้งสิ้น เดิมที่ National Science Foundation (NSF) แห่งสหรัฐอเมริกาเรียกกลุ่มวิชาสะเต็มศึกษาว่า SMETตามลำดับการวิวัฒน์ของแต่ละวิชา แต่เนื่องจากอาจมีการออกเสียงคำว่า SMET ผิดเพี้ยนไปในทางไม่เหมาะสม สุดท้ายจึงได้เปลี่ยนมาเป็น STEM แทน (Sanders, 2009)

            ลักษณะสำคัญประการหนึ่งในการศึกษาเรียนรู้แบบสะเต็มศึกษาคือการเชื่อมโยงความรู้ระหว่างวิชาวิทยาศาสตร์คณิตศาสตร์ เทคโนโลยี และกระบวนการออกแบบทางวิศวกรรมเข้าด้วยกัน เพื่อนำไปใช้แก้ปัญหาต่าง ๆ ในชีวิตประจำวันและในโลกของการทำงาน โดยในส่วนของวิชาคณิตศาสตร์ซึ่งศึกษาถึงแบบรูปและความสัมพันธ์ระหว่างจำนวน ปริมาณและ รูปทรงเรขาคณิตต่าง ๆ (Katehi, L., Pearson, G. and Feder, M., 2009) ก็เป็นวิชาที่สามารถนำไปใช้เชื่อมโยงกับวิชาอื่น ๆ ในสะเต็มศึกษาได้อย่างหลากหลาย บทความนี้จะแสดงให้เห็นถึงความสัมพันธ์ระหว่างวิชาคณิตศาสตร์ กับวิชาวิทยาศาสตร์ เทคโนโลยี และการออกแบบทางวิศวกรรม ว่ามีความเชื่อมโยงกันอย่างไร และเป็นการแสดงตัวอย่างของการนำเอาความรู้วิชาคณิตศาสตร์ไปใช้ในกระบวนการต่าง ๆ อย่างมีความหมาย

คณิตศาสตร์กับวิทยาศาสตร์

            วิทยาศาสตร์เป็นวิชาที่มุ่งศึกษาและหาคำอธิบายปรากฏการณ์ทางธรรมชาติต่าง ๆ รอบตัวทั้งทางด้านกายภาพและชีวภาพ รวมถึงการนำความรู้เหล่านั้นมาประยุกต์ใช้ในเรื่องต่าง ๆ วิชาวิทยาศาสตร์นับเป็นวิชาที่มีความสัมพันธ์และเชื่อมโยงกับวิชาคณิตศาสตร์อย่างใกล้ชิด องค์ความรู้ทางคณิตศาสตร์สามารถนำไปใช้สนับสนุนการศึกษาด้านวิทยาศาสตร์ในหลาย ๆ ขั้นตอน ไม่ว่าจะเป็นการวัดปริมาณพื้นฐานต่าง ๆ ทั้งความยาว มวล เวลา อุณหภูมิ ปริมาณสารออกมาเป็นจำนวนเพื่อหาความสัมพันธ์ระหว่างสิ่งต่าง ๆ รวมถึงการเขียนและการเปลี่ยนหน่วยต่าง ๆ เหล่านี้ซึ่งต้องใช้ความรู้ทางคณิตศาสตร์มาเกี่ยวข้อง นอกจากนี้ในการทำการทดลองวิทยาศาสตร์ก็จำเป็นต้องมีการรวบรวมข้อมูลและประมวลผลข้อมูลต่าง ๆ โดยใช้กระบวนการทางสถิติอีกด้วย

            แต่จุดที่น่าสนใจคือปรากฏการณ์ต่าง ๆ ในธรรมชาติที่นักวิทยาศาสตร์พยายามสรุปเป็นกฎหรือทฤษฎีนั้นสามารถนำมาเขียนในรูปสมการทางคณิตศาสตร์ได้หลายกรณี แสดงให้เห็นว่าความสัมพันธ์ทางคณิตศาสตร์เป็นสิ่งที่มีอยู่ในธรรมชาติและมีส่วนช่วยให้นักวิทยาศาสตร์สามารถทำความเข้าใจและทำนายปรากฏการณ์ต่าง ๆ ได้อย่างมีแบบแผนชัดเจนมากยิ่งขึ้น ยกตัวอย่างสูตรแสดงทฤษฎีสัมพัทธภาพของ แอลเบิร์ต ไอน์สไตน์อันโด่งดัง ก็แสดงด้วยสมการทางคณิตศาสตร์

E = mc²

เมื่อ E แทนพลังงานมีหน่วยเป็นจูล
m แทนมวลมีหน่วยเป็นกิโลกรัม
c แทนอัตราเร็วของแสงในสุญญากาศซึ่งมีค่าประมาณ 3 x 10⁸ เมตรต่อวินาที

            ซึ่งนอกจากจะแสดงความสัมพันธ์ระหว่างพลังงาน มวลของสาร และอัตราเร็วของแสงในสุญญากาศแล้ว สูตรแสดงทฤษฎีสัมพัทธภาพนี้ยังแสดงให้เห็นถึงความสัมพันธ์ทางคณิตศาสตร์ของหน่วยการวัดทางวิทยาศาสตร์ด้วยว่า หน่วยของพลังงานเป็นจูล ยังสามารถเขียนให้อยู่ในรูปการคูณและหารของหน่วยพื้นฐานเป็น กิโลกรัม . เมตร² ต่อ วินาที ได้อีกด้วยหรือในการศึกษาเรื่องการแผ่กระจายของกำลังเสียงจากแหล่งกำเนิดเสียงหนึ่ง ๆ นักวิทยาศาสตร์ก็พบว่าการแผ่กระจายของกำลังเสียงจากแหล่งกำเนิดเสียงมีลักษณะการกระจายตัวเป็นรูปทรงกลมทำให้ความเข้มเสียง ณ ตำแหน่งที่อยู่ห่างจากแหล่งกำเนิดเสียงลดลงเรื่อย ๆ ตามความสัมพันธ์ต่อไปนี้

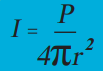
เมื่อ I แทนความเข้มเสียง ณ ตำแหน่งหนึ่ง ๆ มีหน่วยเป็น วัตต์ต่อตารางเมตร
P แทนกำลังเสียงของแหล่งกำเนิดเสียง มีหน่วยเป็น วัตต์
R แทนระยะจากแหล่งกำเนิดเสียงไปยังตำแหน่งที่ต้องการหาค่า I มีหน่วยเป็น เมตร

            ซึ่งจากสมการจะเห็นว่า ตัวส่วน 4πr² ก็คือสูตรพื้นที่ผิวของรูปทรงกลมที่เสียงกระจายตัวไปถึง ณ ตำแหน่งต่าง ๆ นั่นเอง ดังนั้นความเข้มเสียง ณ จุดหนึ่ง ๆ ก็คืออัตราส่วนระหว่างกำลังเสียงของแหล่งกำเนิดเสียงกับพื้นที่ผิวของทรงกลมที่มีจุดศูนย์กลางอยู่ที่แหล่งกำเนิดเสียงและมีรัศมีเท่ากับระยะจากแหล่งกำเนิดเสียงไปยังจุดที่ต้องการหาค่าความเข้มเสียงดังแสดงในรูปที่ 1

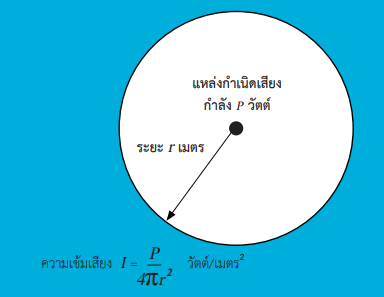
รูปที่ 1 กำลังเสียงที่กระจายตัวเป็นทรงกลม

            จากความสัมพันธ์นี้ จะเห็นว่า เมื่อกำหนดให้ระยะ r คงที่ ความเข้มเสียงจะแปรผันตรงกับกำลังเสียงของแหล่งกำเนิดเสียง

            และในทางกลับกันถ้ากำหนดให้กำลังเสียงของแหล่งกำเนิดเสียงคงที่ ความเข้มเสียง ณ ตำแหน่งต่าง จะแปรผกผันกับกำลังสองของระยะห่างระหว่างแหล่งกำเนิดเสียงกับตำแหน่งนั้น ๆ

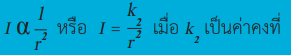
            ดังนั้นหลักการทางวิทยาศาสตร์ที่เกี่ยวข้องกับเรื่องการกระจายของแหล่งกำเนิดเสียงสามารถชื่อมโยงกับเนื้อหาคณิตศาสตร์เรื่องการแปรผัน อัตราส่วนและพื้นที่ผิวของทรงกลมแสดงให้เห็นถึงความสัมพันธ์ทางคณิตศาสตร์ที่มีอยู่ในปรากฏการณ์ทางธรรมชาติซึ่งสามารถนำมาประยุกต์ใช้ในชีวิตประจำวันได้ เช่น การหาระยะที่เหมาะสมสำหรับการติดตั้งลำโพงเพื่อให้ผู้ที่อยู่ห่างออกไปยังสามารถได้ยินได้

            เทคโนโลยีเป็นการนำทรัพยากรที่มีมาสร้างสิ่งของ เครื่องใช้ ผลิตภัณฑ์ หรือวิธีการ ผ่านการทำงานอย่างเป็นกระบวนการ เพื่อช่วยแก้ปัญหาหรือสนองความต้องการของมนุษย์และเพิ่มความสามารถในการทำงานและการดำรงชีวิตให้มีความสะดวกสบาย รวดเร็ว และปลอดภัย จะเห็นว่าเทคโนโลยีมีการพัฒนาอยู่เรื่อย ๆ โดยมีเป้าหมายในการเพิ่ม 'ประสิทธิภาพ' การทำงานให้สูงขึ้น

            ประสิทธิภาพในการสร้างสรรค์เทคโนโลยีสามารถแสดงด้วยความสัมพันธ์ทางคณิตศาสตร์ในรูปของอัตราส่วนระหว่างสองตัวแปรคือ ผลที่ได้ และ ทรัพยากรที่ใช้

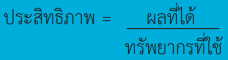
            ดังนั้นการเพิ่มประสิทธิภาพของผลิตภัณฑ์หรือการทำงานจึงสามารถทำได้ด้วยการเพิ่มตัวเศษซึ่งก็คือ ผลที่ได้ โดยใช้ทรัพยากรเท่าเดิม หรือการลดตัวส่วนซึ่งก็คือทรัพยากรที่ใช้โดยให้ได้ผลที่ได้เท่าเดิม หรือ เพิ่มผลที่ได้โดยลดทรัพยากรที่ใช้ไปพร้อม ๆ กัน

            การคำนวณประสิทธิภาพของผลิตภัณฑ์หรือการทำงานออกมาเป็นอัตราส่วนนี้ ทำให้เราสามารถเปรียบเทียบประสิทธิภาพของผลิตภัณฑ์หรือวิธีการทำงานต่างชนิดหรือต่างวิธีได้อย่างชัดเจนมากยิ่งขึ้น

            ตัวอย่างของการพัฒนาด้านเทคโนโลยีเพื่อให้ประสิทธิภาพของผลิตภัณฑ์และการทำงานสูงขึ้น สามารถเห็นได้ชัดจากเทคโนโลยีสารสนเทศที่วิวัฒน์ไปอย่างรวดเร็ว เช่น การพัฒนาวิธีส่งข้อมูลดิจิทัลผ่านสายโทรคมนาคมที่เดิมทีใช้กระแสไฟฟ้าวิ่งผ่านสายทองแดงเช่นสายโทรศัพท์ในการส่ง แต่ต่อมาเริ่มมีการใช้เส้นใยนำแสง (optical fibre) ซึ่งส่งด้วยลำแสงทำให้ความเร็วในการส่งสูงขึ้นเท่าความเร็วแสงและให้สัญญาณที่มีความเสถียรมากกว่าสายทองแดงเนื่องจากไม่มีความต้านทานเข้ามาเกี่ยวข้อง ซึ่งหลังจากมีการหันมาใช้ใยนำแสงในการส่งข้อมูลแล้ว นักเทคโนโลยีก็ได้พัฒนาประสิทธิภาพในการส่งข้อมูลผ่านใยนำแสงด้วยการใช้หลักการสะท้อนของแสงกับเรื่องมุมแย้งของเส้นขนานมาประยุกต์ใช้เพื่อให้ใยนำแสงเพียงเส้นเดียวสามารถส่งสัญญาณได้หลายช่องพร้อม ๆ กันด้วยการทำให้ลำแสงหลายลำแสงทำมุมต่าง ๆ กับแกนเส้นผ่านศูนย์กลางของใยแก้ว ดังแสดงในรูปที่ 2

รูปที่ 2 การพัฒนาประสิทธิภาพการส่งข้อมูลผ่านเส้นใยนำแสงด้วยการใช้หลักการสะท้อนแสงและมุมแย้งของเส้นขนาน
เพื่อให้สามารถส่งข้อมูลได้หลายช่องทางมากขึ้นจากสายเพียงเส้นเดียว

            ซึ่งถึงแม้ว่าลำแสงที่ส่งผ่านการสะท้อนด้วยมุมต่าง ๆ จะใช้ระยะทางในการเดินทางของแสงมากกว่าลำแสงที่ส่งไปตามแกนเส้นผ่านศูนย์กลางของสายดังแสดงในรูป แต่เนื่องจากแสงมีความเร็วสูงมาก ความแตกต่างนี้จึงไม่มีนัยสำคัญนัก

            นอกจากนี้นักเทคโนโลยียังสามารถตรวจสัญญาณช่องต่าง ๆ ได้จากมุมของลำแสงที่แตกต่างกันได้ว่าลำแสงใดแทนช่องสัญญาณใด การนำเอาหลักการสะท้อนของแสงและความรู้คณิตศาสตร์เรื่องมุมแย้งในเส้นขนานมาประยุกต์ใช้จึงช่วยในการเพิ่มประสิทธิภาพด้วยจำนวนช่องสัญญาณที่ส่งได้มากขึ้นจากใยนำแสงเพียงเส้นเดียวนั่นคือ เพิ่มผลที่ได้ โดยใช้ทรัพยากรเท่าเดิม

            นอกเหนือจากการเพิ่มประสิทธิภาพด้วยการเพิ่มผลที่ได้โดยใช้ทรัพยากรเท่าเดิมแล้ว ประสิทธิภาพยังสามารถเพิ่มได้ด้วยการลดทรัพยากรที่ใช้โดยยังได้ผลที่ต้องการเท่าเดิมดังจะเห็นได้จากตัวอย่างการพัฒนาเทคโนโลยีของจอแสดงผลของเครื่องคอมพิวเตอร์ที่แต่เดิมนิยมใช้จอ Cathode Ray Tube CRT) โดยอาศัยหลักการยิงลำอิเล็กตรอนไปยังผิวด้านในของจอภาพซึ่งฉาบด้วยสารฟอสฟอรัส ทำให้ตำแหน่งที่อิเล็กตรอนวิ่งมาชนเกิดแสงสว่างขึ้น ซึ่งจำเป็นต้องแปลงความต่างศักย์ไฟฟ้า 220 โวลต์ให้สูงขึ้นหลายเท่าเพื่อการยิงลำอิเล็กตรอนทำให้สิ้นเปลืองพลังงานไฟฟ้ามาก ต่อมานักเทคโนโลยีจึงได้พัฒนาจอแสดงผลแบบใหม่คือจอ Liquid Crystal Display (LCD) ซึ่งใช้หลักการปรับเปลี่ยนโมเลกุลของผลึกเหลวเพื่อปิดกั้นแสงเมื่อมีสนามไฟฟ้าเหนี่ยวนำ ทำให้ใช้กำลังไฟฟ้าต่ำและสามารถประหยัดพลังงานลงไปมาก โดยจอ CRT ขนาด 17 นิ้ว (วัดความยาวตามเส้นทแยงมุม ทำให้มีพื้นที่ประมาณ 70 ตารางนิ้วสำหรับจอที่มีอัตราส่วนความยาวต่อความกว้างเป็น4:3) รุ่นหนึ่งของบริษัทหนึ่งอาจกินไฟถึง 125 วัตต์ ในขณะที่จอ LCD ขนาดเดียวกันอาจกินไฟเพียง 35 วัตต์เท่านั้น เมื่อเปรียบเทียบประสิทธิภาพกำลังไฟฟ้ากับการแสดงผลของจอทั้งสองแบบแล้วจะได้ว่า

            และนอกเหนือจากการประหยัดพลังงานแล้ว จอแบบ LCD ยังใช้กลไกในการแสดงภาพน้อยกว่า ทำให้ช่วยลดขนาดความลึกของจอได้อีกหลายเท่าและประหยัดพื้นที่ในการทำงานไปได้มาก

รูปที่ 3 การพัฒนาเทคโนโลยีจากจอแสดงผลแบบ CRT ม้าเป็นจอแบบ LCD
ซึ่งนอกจากจะประหยัดพลังงานแล้วยังประหยัดพื้นที่การทำงานได้อีกด้วย (ที่มา: http://www.computri.net)

            หลักการของประสิทธิภาพที่สามารถแสดงได้ด้วยอัตราส่วนทางคณิตศาสตร์จึงสามารถนำมาใช้เป็นตัวบ่งชี้พัฒนาการทางเทคโนโลยีได้เป็นอย่างดี ว่านวัตกรรมใหม่ที่สร้างขึ้นมานั้นได้ปรับปรุงการทำงานให้ดีขึ้นเท่าใด

คณิตศาสตร์กับการออกแบบทางวิศวกรรม

            จุดเน้นสำคัญของการเรียนรู้แบบสะเต็มศึกษาคือการนำความรู้ทางคณิตศาสตร์ วิทยาศาสตร์ หรือเทคโนโลยีมาบูรณาการเพื่อประยุกตีใช้ในการแก้ปัญหาในชีวิตจริงผ่านกระบวนการออกแบบทางวิศวกรรม ลักษณะสำคัญของการแก้ปัญหาทางวิศวกรรม คือ

• เป็นปัญหาที่เกิดขึ้นในบริบทของสถานการณ์จริงภายใต้เงื่อนไขและข้อจำกัดต่าง ๆ
• วิธีการแก้ปัญหาสามารถบรรลุสิ่งที่ต้องการได้จริงภายใต้เงื่อนไขและข้อจำกัดเหล่านั้น
• อาจมีวิธีการแก้ปัญหาได้หลายวิธี และควรมีกระบวนการเพื่อหาวิธีที่ให้ประสิทธิภาพมากที่สุด

            เนื่องจากในการแก้ปัญหาทางวิศวกรรมนั้น มุ่งเน้นผลลัพธ์ที่มีประสิทธิภาพและสามารถนำไปใช้ได้จริง วิศวกรจึงจำเป็นต้องใช้ความรู้ทางคณิตศาสตร์มาใช้ร่วมกับความรู้ทาง

            วิทยาศาสตร์และเทคโนโลยีในการแก้ปัญหา และเนื่องจากปัญหาทางวิศวกรรมมักจะมีวิธีการแก้ปัญหาได้หลายวิธี วิศวกรจึงจำเป็นต้องเป็นผู้รอบรู้ในเนื้อหาวิชาคณิตศาสตร์เพื่อให้สามารถนำความรู้เหล่านั้นมาใช้แก้ปัญหาได้อย่างหลากหลายดังตัวอย่างการออกแบบโครงสร้างสะพานข้ามแม่น้ำแห่งหนึ่งซึ่งสามารถทำได้หลายวิธี แต่วิศวกรสามารถนำความรู้เกี่ยวกับรูปเรขาคณิตและหลักการถ่ายทอดของแรงมาออกแบบโครงสร้างสะพานได้ ดังแสดงในรูปที่ 4

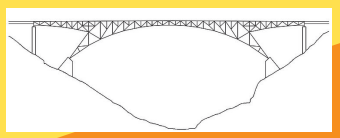
รูปที่ 4 การออกแบบโครงสร้างสะพานข้ามแม่น้ำของวิศวกรโดยใช้รูปสามเหลี่ยมชนิดต่าง ๆ
(ที่มา: http:/www.highestbridges.com)

            จะเห็นได้ว่าวิศวกรได้เลือกใช้รูปสามเหลี่ยมชนิดต่าง ๆทั้งสามเหลี่ยมมุมแหลม สามเหลี่ยมมุมฉาก และสามเหลี่ยมมุมป้าน มาเป็นส่วนประกอบย่อยในการออกแบบโครงสร้างทั้งหมดโดยไม่มีรูปหลายเหลี่ยมอื่น ๆ เลย เนื่องจากโครงสร้างที่ใช้รูปสามเหลี่ยมจะกระจายแรงได้อย่างสมดุลมากกว่ารูปอื่น ๆ ตามหลักทางฟิสิกส์ ซึ่งการออกแบบโครงสร้างด้วยสามเหลี่ยมชนิดต่าง ๆ เหล่านี้ ทำให้วิศวกรต้องใช้ความรู้เกี่ยวกับสามเหลี่ยมเรื่องต่าง ๆ ทั้งเรื่องความคล้าย ความเท่ากันทุกประการ ทฤษฎีบทพีทาโกรัส และตรีโกณมิติ รวมถึงความรู้เรื่องเวกเตอร์ มาใช้ในการคำนวณเพื่อออกแบบโครงสร้างอย่างไรก็ดีวิศวกรอาจออกแบบสะพานด้วยรูปสามเหลี่ยมเพียงอย่างเดียวที่มีลักษณะแตกต่างออกไปได้อีกโดยแต่ละวิธีอาจมีประสิทธิภาพในการรับแรงที่แตกต่างกัน

            ประสิทธิภาพและความคุ้มค่านับเป็นปัจจัยที่สำคัญในการออกแบบทางวิศวกรรม โดยวิศวกรจะพยายามออกแบบกระบวนการแก้ปัญหาที่สามารถให้ผลลัพธ์ปริมาณมากโดยใช้ทรัพยากรที่มีอยู่ให้น้อยที่สุด ความรู้คณิตศาสตร์ด้านแคลคูลัส โดยเฉพาะเรื่องการหาอนุพันธ์เพื่อหาค่าสูงสุดหรือต่ำสุดจึงเป็นเครื่องมือทางคณิตศาสตร์ที่สำคัญอีกหนึ่งอย่างของวิศวกรที่สามารถช่วยในการหาว่าวิธีการแก้ปัญหาใดจะทำให้ได้ค่า optimum value หรือค่าที่เหมาะสมที่สุดสำหรับปัญหาหนึ่ง ๆ ยกตัวอย่างการใช้ค่าอนุพันธ์ช่วยในการหาคำตอบของปัญหาในชีวิตประจำวัน เช่น หากมีแผ่นอะลูมิเนียมรูปสี่เหลี่ยมจัตุรัสความยาวด้านละ 10 นิ้ว และต้องการตัดมุมทั้งสี่ออกไปเป็นรูปสี่เหลี่ยมจัตุรัสที่มีขนาดเท่ากัน เพื่อพับและเชื่อมแผ่นอะลูมิเนียมส่วนที่เหลือเป็นภาชนะรูปทรงสี่เหลี่ยมมุมฉากเปิดด้านบน ควรตัดรูปสี่เหลี่ยมจัตุรัสตรงมุมทั้งสี่ออกไปให้มีขนาดเท่าใดจึงจะได้ความจุของภาชนะมากที่สุด

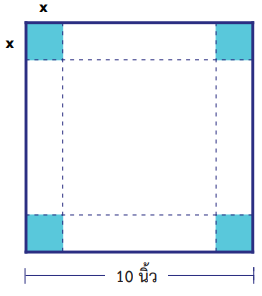
            เราสามารถหาความยาวของด้านของสี่เหลี่ยมจัตุรัสที่ต้องตัดออกได้ ด้วยการกำหนดให้ความยาวด้านของรูปสี่เหลี่ยมจัตุรัสที่ต้องการตัดออกเป็น x หน่วยแล้ว เขียนฟังก์ชัน f(x) ของปริมาตรภาชนะได้เป็น

            จากนั้นหาตำแหน่งของค่า x ที่ทำให้ค่าอนุพันธ์ f'^/(x) หรือค่าความชันของกราฟฟังก์ชัน f(x) เป็นศูนย์ จะได้คำตอบว่าค่าวิกฤตของฟังก์ชัน   นั่นคือควรตัดมุมของแผ่นอะลูมิเนียมออกเป็นรูปสี่เหลี่ยมจตุรัสความยาวด้านละ   จะได้ภาชนะอะลูมิเนียมที่มีความจุมากที่สุดจากหลักการเดียวกันนี้วิศวกรสามารถใช้การหาคำอนุพันธ์ช่วยในการออกแบบสิ่งต่าง ๆ เพื่อให้เกิดประโยชน์อย่างคุ้มค่าที่สุดจากทรัพยากรที่มีอยู่ได้

            อย่างไรก็ดีการแก้ปัญหาทางวิศวกรรมในส่วนของสะเต็มศึกษานั้น ไม่จำเป็นจะต้องเป็นปัญหาระดับสูงที่วิศวกรมีหน้าที่แก้ปัญหาในการทำงานจริง แต่อาจเป็นปัญหาในชีวิตประจำวันซึ่งสามารถใช้กระบวนการทางคณิตศาสตร์ วิทยาศาสตร์และเทคโนโลยี ช่วยในการแก้ปัญหา โดยในการแก้ปัญหาทางวิศวกรรมนั้นอาจไม่จำเป็นต้องใช้ความรู้ทั้งทางวิทยาศาสตร์คณิตศาสตร์ และเทคโนโลยี พร้อมกันทั้งหมด แต่อาจเลือกใช้เพียงบางด้านก็ได้ ดังนั้นนักเรียนก็สามารถแก้ปัญหาทางวิศวกรรมได้ หากมีการใช้ความรู้ทางวิทยาศาสตร์ คณิตศาสตร์หรือเทคโนโลยีมาช่วยในการแก้ปัญหาอย่างมีกระบวนการโดยไม่ได้ใช้วิธีลองผิดลองถูกแต่เพียงอย่างเดียว

            จากตัวอย่างทั้งหมดในบทความนี้ คงแสดงให้เห็นแล้วว่าคณิตศาสตร์มีความสัมพันธ์อย่างใกล้ชิดต่อวิชาวิทยาศาสตร์เทคโนโลยี และการออกแบบทางวิศวกรรมในกลุ่มวิชาสะเต็มศึกษาเพียงใดและคงทำให้เห็นว่าวิชาคณิตศาสตร์ที่ดูเหมือนเป็นเรื่องนามธรรมและห่างไกลจากชีวิตจริงนั้น แท้แล้วกลับเป็นเครื่องมือสำคัญในการศึกษาวิชาความรู้ด้านต่าง ๆ รวมทั้งการนำไปใช้ในการแก้ปัญหาอย่างขาดไปไม่ได้เลยทีเดียว

            บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://magazine.ipst.ac.th/

บรรณานุกรม

Bybee, R. W. (2011). Scientific and Engineering Practices in K-12 Classrooms: Understanding A Framework for K-12 Science Education. Science Teacher, 78(9), 34-40.

Katehi, L., Pearson, G. & Feder, M. (2009). Engineering in K-12 Education: Understanding the Status and Improving the Prospects. Washington, D.C.: NationalAcademies Press.

Sanders, M. (2009). STEM, STEM Education, STEMmania. The Technology Teacher, 68(4), 20-26.

Williams, J. (2011). STEM Education: Proceed with Caution. Design and Technology Education: An International Journal. 16(1), 26-35.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2552). หนังสือเรียนรายวิชาพื้นฐานเทคโนโลยีสารสนทศและการสื่อสาร ชั้นมัธยมศึกษาปีที่ 1.กรุ๊งเทพมหานคร :โรงพิมพ์ สกสค. ลาดพร้าว.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. กระทรวงศึกษาธิการ. (2554). หนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์เล่ม 6 ชั้นมัธยมศึกษาปีที่ 4-6. กรุงเทพมหานคร: โรงพิมพ์สกสค. ลาดพร้าว.