เนื่องจากปัญหาอาชญากรรมที่เกิดขึ้นมากมายในปัจจุบันไม่ว่าจะเป็นการโจรกรรม การทำร้ายร่างกาย และการฆาตกรรมทำให้มีความจำเป็นที่จะต้องหาตัวผู้กระทำความผิดมาลงโทษตามกฎหมาย โดยอาศัยการตรวจพิสูจน์หลักฐานต่าง ๆ ด้วยความรู้ทางวิทยาศาสตร์และเทคโนโลยีเพื่อหาหลักฐานยืนยันความผิดของบุคคลเหล่านั้น ทำให้มีความต้องการผู้เชี่ยวชาญเฉพาะด้านการพิสูจน์หลักฐาน และเกิดสาขาวิชาใหม่ขึ้น คือ นิติวิทยาศาสตร์ (Forensic Science) โดยจะเน้นที่การนำความรู้ทางคณิตศาสตร์ ฟิสิกส์ เคมี ชีววิทยา กีฎวิทยา และเทคโนโลยี ไปประยุกต์ใช้ในการสืบสวนคดีต่าง ๆ

            วิธีทางนิติวิทยาศาสตร์วิธีหนึ่งที่นำเสนอ คือ การใช้ความรู้ทางคณิตศาสตร์ในการหาตำแหน่งที่เหยื่อถูกทำร้ายจากการกระจายตัวของหยดเลือดและนำไปสู่การอธิบายเหตุการณ์ที่เกิดขึ้นในที่เกิดเหตุได้ เช่น เจ้าหน้าที่นิติวิทยาศาสตร์สามารถใช้รอยเลือดสันนิษฐานเหตุการณ์ในห้องที่เกิดการฆาตกรรมและคาดการณ์ได้ว่าผู้ตายถูกทำร้ายที่ตำแหน่งใดของห้อง มีการขัดขืนหรือไม่ หรือมีการต่อสู้กันเกิดขึ้นในที่เกิดเหตุหรือไม่ หรือเป็นการจัดฉากเพื่ออำพรางคดี โดยใช้ความรู้เกี่ยวกับตรีโกณมิติที่เรียนในระดับมัธยมศึกษาปีที่ 5

            ก่อนอื่นพิจารณาหยดเลือดที่มีลักษณะเป็นทรงกลมเคลื่อนที่ไปในอากาศ กระทบกับพื้นผิวไม่ว่าจะเป็นพื้น ผนัง หรือเพดานถ้าหยดเลือดนี้เคลื่อนที่ในแนวตั้งฉากกับพื้นผิว เลือดจะกระจายตัวออกไปทุกทิศทุกทางเท่ากัน และจะได้รอยเลือดที่มีลักษณะเป็นรูปวงกลม แล้วจะเกิดอะไรขึ้น ถ้าหยดเลือดเคลื่อนที่ทำมุมกับพื้นผิวน้อยกว่า 90^๐

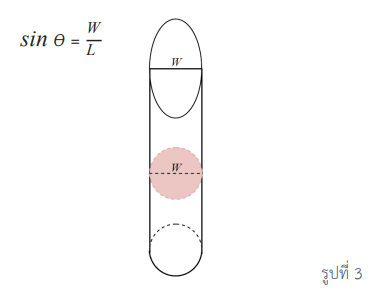
            ในความเป็นจริง เมื่อเกิดคดีฆาตกรรม เลือดมักจะออกมาจากตัวเหยื่อ แล้วกระเด็นไปโดนพื้นผิวต่าง ๆ โดยการเคลื่อนที่นี้จะทำมุมกับพื้นผิว ถ้าหยดเลือดเคลื่อนที่โดยทำมุม q ซึ่งมีค่าน้อยกว่า 90^๐ (0 < q <90^๐ ) เมื่อหยดเลือดกระทบกับพื้นผิวเลือดจะกระจายตัวและยืดออกไปตามทิศทางการเคลื่อนที่ ซึ่งรอยเลือดจะมีลักษณะเป็นรูปวงรี ดังรูปที่ 1 และเมื่อกำหนดให้ W แทนความกว้างของรอยเลือด และ L แทนความยาวของรอยเลือด ดังรูปที่ 2 จะได้ว่าความกว้างของรอยเลือดเท่ากับความยาวของเส้นผ่านศูนย์กลางของหยดเลือด เมื่อถึงจุดนี้ผู้อ่านอาจสงสัยว่าทำไมความกว้างของรอยเลือดจึงเท่ากับความยาวของเส้นผ่านศูนย์กลางของหยดเลือด

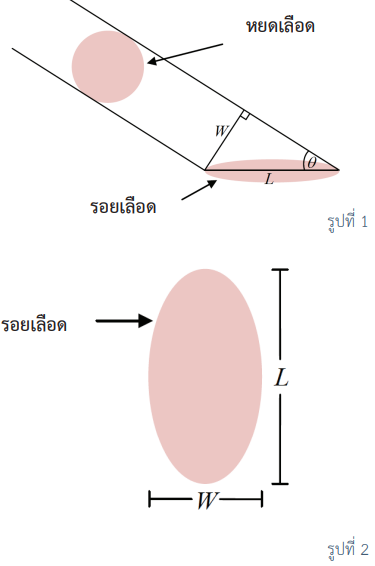
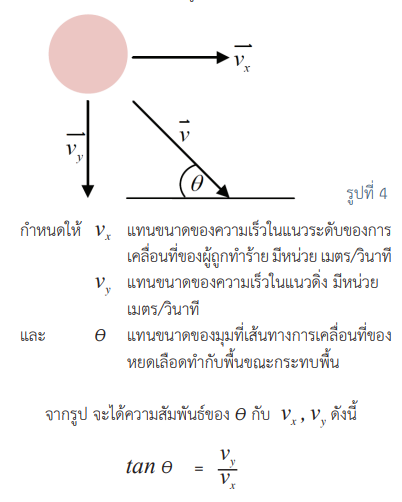
            ถ้าเปรียบเส้นทางการเคลื่อนที่ของหยดเลือดเป็นท่อทรงกระบอกที่ตอนปลายของท่อมีหน้าตัดเป็นรูปวงรี ดังรูปที่ 3 จะได้ว่าความยาวของเส้นผ่านศูนย์กลางของหยดเลือดเท่ากับความกว้างของรูปวงรี และจากรูปที่ 1 จะสามารถหาขนาดของมุมที่เส้นทางการเคลื่อนที่ของหยดเลือดทำกับพื้นเมื่อทราบความกว้างและความยาวของรอยเลือดได้ เมื่อ q แทนขนาดของมุมที่เส้นทางการเคลื่อนที่ของหยดเลือดทำกับพื้น จะได้

            พิจารณาหยดเลือดที่เคลื่อนที่ออกมาจากผู้ถูกทำร้าย เมื่อเลือดตกกระทบพื้นด้วยแรงโน้มถ่วงของโลกในขณะที่ผู้ถูกทำร้ายยังเคลื่อนที่จะมีแรงในแนวนอนเกิดขึ้น ดังนั้น เมื่อเลือดกระทบกับพื้น จึงทำให้เกิดมุมที่เส้นทางการเคลื่อนที่ของหยดเลือดทำกับพื้นไม่ใช่ 90^๐ ดังรูปที่ 4

            ซึ่งสามารถนำสมการนี้ไปใช้คำนวณความเร็วของการเคลื่อนที่ของผู้ถูกทำร้าย จากการวัดมุมที่เลือดตกกระทบพื้นส่วนขนาดของความเร็วในแนวตั้งที่แทนด้วย V_y จะคำนวณโดยใช้ความสูงจากพื้นถึงจุดกำเนิดเลือด เช่น หัว แขน ลำตัวหรือขา โดย

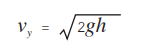
            เมื่อ h แทนความสูงจากพื้นถึงจุดกำเนิดเลือดและ g แทนค่าความเร่งเนื่องจากแรงโน้มถ่วงของโลก (สมมตีให้แรงต้านทานอากาศไม่ส่งผลอย่างมีนัยสำคัญ ซึ่งจะเป็นจริงสำหรับหยดเลือดขนาดใหญ่ซึ่งเคลื่อนที่ลงมาด้วยระยะทางสั้น ๆ)

            ตัวอย่างการนำความรู้ทางนิติวิทยาศาสตร์ไปประยุกต์ใช้ในการหาข้อเท็จจริงเพื่อใช้ในการสืบสวนต่าง ๆ เช่น

            รูปแบบการกระจายตัวของรอยเลือดถูกกำหนดโดยการกระทบของหยดเลือดจำนวนมากบนพื้นผิว ซึ่งบ่อยครั้งจะเกิดขึ้นพร้อมกันจากจุดกำเนิดเลือดเดียวกัน เช่น การตีที่ศีรษะหรือแผลจากการถูกยิง หยดเลือดต่าง ๆ จะกระทบพื้นในมุมที่ต่างกัน ซึ่งวิธีการหนึ่งในการหาจุดกำเนิดเลือดจากรูปแบบการกระจายตัวของรอยเลือด ทำได้โดยใช้ความรู้เรื่องตรีโกณมิติมาพิจารณาเส้นทางการเคลื่อนที่ โดยจะกำหนดให้เส้นทางการเคลื่อนที่เป็นแนวตรง และไม่พิจารณาความเร่งโน้มถ่วง ในทางปฏิบัติ การวิเคราะห์รูปแบบการกระจายตัวของรอยเลือดจะใช้เชือกตรึงจุดที่เกิดรอยเลือดไปหาจุดที่เกิดเหตุ หรือใช้โปรแกรมคอมพิวเตอร์วิเคราะห์ ซึ่งการคำนวณนี้ใช้เพียงแค่ความรู้พื้นฐานทางตรีโกณมิติ โดยมีขั้นตอน ดังนี้

1. ระบุกลุ่มของรอยเลือดที่เหมาะสมและการคำนวณหามุมที่ตกกระทบของรอยเลือดกลุ่มนี้
2. พิจารณาจุดตัดของเส้นที่ลากผ่านแกนสมมาตรที่ยาวที่สุดของรอยเลือดบนพื้นผิว
3. พิจารณาจุดตัดของเส้นทางการเคลื่อนที่ของรอยเลือดที่มาบรรจบกันในปริภูมิสามมิติ หรือพิจารณาหาจุดกำเนิดเลือด

            ในการคำนวณหาจุดกำเนิดเลือดจะต้องพิจารณารอยเลือด 2 รอย ดังตัวอย่างต่อไปนี้

ตัวอย่างที่ 2

            เกิดเหตุการทำร้ายร่างกายภายในห้อง เมื่อตำรวจไปถึงที่เกิดเหตุก็ไม่พบทั้งผู้ทำร้ายและผู้ถูกทำร้าย แต่พบรอยเลือดจำนวนหนึ่งบนผนัง เพื่อที่จะหาจุดที่เหยื่อถูกทำร้าย

            เจ้าหน้าที่นิติวิทยาศาสตร์จึงได้เลือกรอยเลือด 2 รอย คือรอยเลือด A และรอยเลือด B ซึ่งจากการตรวจสอบพบว่ารอยเลือด A กว้าง 3.8 มิลลิเมตร ยาว 5 มิลลิเมตรรอยเลือด B กว้าง 4.5 มิลลิเมตร ยาว 5.7 มิลลิเมตรรอยเลือด A และรอยเลือด B อยู่ห่างกัน 75 เชนติเมตรเมื่อลากเส้นผ่านแกนสมมาตรที่ยาวที่สุดของรอยเลือดA และรอยเลือด B ให้ตัดกันที่จุด C ดังรูปที่ 5 และเมื่อวัดขนาดของมุม A และ B ได้ α= 65^o และ β = 80^o ตามลำดับ จงหาว่าจุดที่เหยื่อถูกทำร้ายอยู่ห่างจากผนังเท่าใด

            หมายเหตุ จุด A, B และ C เป็นจุดที่อยู่บนระนาบเดียวกัน ซึ่งอาจจะอยู่บนพื้นหรือผนังก็ได้จากที่กล่าวมาแล้วจะเห็นว่าการหาตำแหน่งที่มีการทำร้ายกันทำได้ไม่ยาก แต่การหาตำแหน่งที่ถูกทำร้ายยังไม่เพียงพอต่อการพิจารณาคดี ซึ่งจำเป็นต้องมีหลักฐานสำคัญอื่น ๆ อีก เช่น รอยนิ้วมือการระบุ DNA ของผู้กระทำความผิดในที่เกิดเหตุ การหาขนาดและชนิดของแมลงบนศพซึ่งจะทำให้ทราบเวลาเสียชีวิตและอาจจะบอกถึงสถานที่เกิดเหตุด้วย ดังนั้น ผู้ที่ศึกษานิติวิทยาศาสตร์จึงต้องมีความรอบรู้ทางด้านคณิตศาสตร์ และวิทยาศาสตร์แขนงต่าง ๆ

            จากบทความนี้จะเห็นว่าเราสามารถนำความรู้คณิตศาสตร์ระดับพื้นฐานไปช่วยในการคลี่คลายคดีอาชญากรรมที่มีอยู่ในปัจจุบันได้ ผู้เขียนจึงหวังเป็นอย่างยิ่งว่าบทความนี้จะช่วยจุดประกายให้ผู้อ่านเสาะหาลู่ทางในการนำคณิตศาสตร์ไปประยุกต์ใช้กับการแก้ปัญหาอื่น ๆ ในชีวิตจริง ให้ครั้งหน้าผู้เขียนจะนำเรื่องที่น่าสนใจมาเล่าสู่กันฟังอีกนะคะ

           บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://emagazine.ipst.ac.th/

บรรณานุกรม

Adam. Craig. (2010). Essential Mathematics and Statistics for Forensic Science. Wiltshire: Wiley - Blackwell.

Blood splatter.  สืบต้นเมื่อ 1 พฤศจิกายน 2556, จาก http://cmb.physics.wisc.edu/people/gautt/Blood%20$platter%20Trig.pdf

Bloodstain. สืบต้นเมื่อ 1 พฤศจิกายน 2556, จาก http://en.wkpedla.org/wik/Bloodstaln_pattern_analysis

Forensic. สืบต้นเมื่อ 1 พฤศจิกายน 2556, จาก http://www.math.wu.edu/-mays/AVdamo/Labs/Forenslc.pdf