โลกยุคปัจจุบันความปลอดภัยของข้อมูล เป็นเรื่องที่บุคคลและองค์กรให้ความสำคัญในลำดับต้น ๆ และมีมาตรการป้องกันข้อมูลที่หลากหลาย เพื่อเพิ่มความปลอดภัยของข้อมูลการเข้ารหัสข้อมูล (Data Encryption) เป็นวิธีการหนึ่งในการรักษาและป้องกันข้อมูล ให้มีความปลอดภัยไม่ให้บุคคลอื่นล่วงรู้หรือเข้าถึงข้อมูลนี้ได้ การพัฒนาการเข้ารหัสข้อมูลมีมาอย่างยาวนาน โดยมีการใช้งานอย่างแพร่หลายในระหว่างสงครามโลกครั้งที่ 2

คณิตศาสตร์ในระดับมัธยมศึกษาตอนปลายมีการกล่าวถึงการเข้ารหัสข้อมูลหรือไม่ อย่างไร

   ในหนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 5 เล่ม 1 ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐานพุทธศักราช 2551 (ฉบับปรับปรุง พ.ศ. 2560) ของ สสวท. ได้กล่าวไว้ว่า “วิทยาการเข้ารหัสลับ (Cryptography) เป็นศาสตร์ที่ศึกษาวิธีการรักษาความปลอดภัยของข้อมูล ในการสื่อสารระหว่างสองฝ่ายโดยไม่ให้บุคคลอื่นล่วงรู้ด้วยการเข้ารหัส โดยผู้ส่งสารจะใช้รหัสลับซึ่งรู้เฉพาะผู้ส่งสารและผู้รับสารในการแปลงข้อความที่ต้องการสื่อสารเป็นข้อความใหม่ หรือที่เรียกว่า ข้อความที่ถูกเข้ารหัส เมื่อผู้รับสารได้รับข้อความที่ถูกเข้ารหัส ก็จะสามารถถอดรหัสหรือแปลงข้อความที่ถูกเข้ารหัสกลับไปเป็นข้อความดั้งเดิมได้ เนื่องจากบุคคลอื่นไม่รู้รหัสลับซึ่งใช้ในการเข้ารหัส จึงไม่สามารถเข้าใจข้อความนั้นได้ ทำให้ข้อมูลที่ต้องการสื่อสารปลอดภัย” นั่นคือ วิทยาการเข้ารหัสลับ เป็นวิชาที่ว่าด้วยการเข้ารหัสข้อมูลและการถอดรหัสข้อมูล ซึ่งสามารถเขียนแสดงเป็นแผนภาพขั้นตอนได้ดังนี้

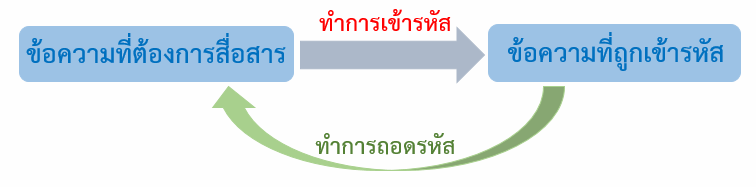
แผนภาพขั้นตอนการเข้ารหัส

   การเข้ารหัสข้อความมีหลากหลายวิธี วิธีการหนึ่งที่เป็นที่นิยม คือ การประยุกต์ใช้ความรู้เกี่ยวกับเมทริกซ์ ในหนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ ชั้นมัธยมศึกษาปีที่ 5 เล่ม 1 ของ สสวท. ได้นิยามเกี่ยวกับเมทริกซ์ ดังนี้

   ดังนั้น หากต้องการนำข้อความมาเขียนในรูปของเมทริกซ์ จำเป็นจะต้องแปลงพยัญชนะ สระ วรรณยุกต์ และเครื่องหมายต่าง ๆ ของข้อความให้เป็นจำนวน โดยทั่วไปการกำหนดจำนวนแทนพยัญชนะ สระ วรรณยุกต์ และเครื่องหมายต่าง ๆ มีด้วยกันหลากหลายระบบ เช่น Binary Code Decimal (BCD), American Standard Code for Information Interchange (ASCII), Unicode ในที่นี้จะนำเสนอการใช้ระบบ Unicode ในการแปลงพยัญชนะ สระ วรรณยุกต์ และเครื่องหมายต่าง ๆ ของข้อความให้เป็นจำนวนเนื่องจากระบบ Unicode ครอบคลุมภาษาที่ใช้กันโดยทั่วไปทั้งโลก รวมทั้งภาษาไทยด้วย เรียกผลจากการแปลงนี้ว่า ชุดลำดับของจำนวน

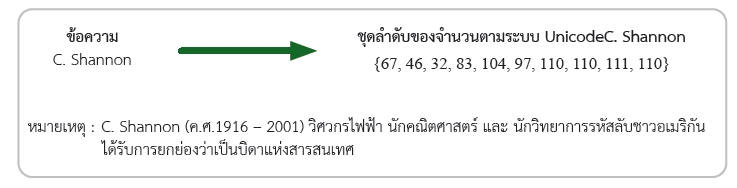
   เมทริกซ์ที่สมาชิกแต่ละตัวเป็นจำนวนที่เกิดจากการแปลงข้อความเป็นชุดลำดับของจำนวนตามระบบ Unicode เรียกว่าเมทริกซ์ข้อความ M

   หากนำจำนวนจริง c ที่ไม่เป็นศูนย์ คูณกับเมทริกซ์ข้อความ M เพื่อเป็นการเข้ารหัสข้อความ จะพบว่าข้อความที่ถูกเข้ารหัสมีความปลอดภัยน้อย เนื่องจากการคาดเดาจำนวนจริง c ซึ่งเป็นจำนวนจริงเพียงจำนวนเดียวนั้น ไม่ได้เป็นการยากมากนัก ดังนั้นหากต้องการเพิ่มความปลอดภัยของข้อความที่ถูกเข้ารหัสให้มากขึ้น โดยไม่ให้บุคคลอื่นสามารถคาดเดาการเข้ารหัสได้ง่าย ควรเลือกการเข้ารหัสข้อความโดยใช้เมทริกซ์ เรียกเมทริกซ์นี้ว่า เมทริกซ์เข้ารหัส E วิธีหนึ่งในการเข้ารหัสข้อความโดยใช้เมทริกซ์ คือการนำเมทริกซ์เข้ารหัส E คูณกับเมทริกซ์ข้อความ M เรียกเมทริกซ์ผลลัพธ์จากการคูณนี้ว่า เมทริกซ์ผลลัพธ์  X

   จากการที่ต้องนำเมทริกซ์เข้ารหัส E คูณกับเมทริกซ์ข้อความ M เพื่อให้ได้เมทริกซ์ผลลัพธ์ X ซึ่งเมทริกซ์ผลลัพธ์ X จะหาได้จากการที่ต้องนำเมทริกซ์เข้ารหัส E คูณกับเมทริกซ์ข้อความ M

   เพื่อให้ได้เมทริกซ์ผลลัพธ์ X ซึ่งเมทริกซ์ผลลัพธ์ X จะหาได้ก็ต่อเมื่อ จำนวนหลักของเมทริกซ์เข้ารหัส E จะต้องเท่ากับจำนวนแถวของเมทริกซ์ข้อความ M

   จะเห็นว่า หากเมทริกซ์เข้ารหัส E มีเมทริกซ์ผกผัน เมื่อนำเมทริกซ์ผกผันของเมทริกซ์เข้ารหัส E มาคูณกับเมทริกซ์ผลลัพธ์ X ผลคูณที่จะได้คือเมทริกซ์ข้อความ M ซึ่งเป็นไปตามสมบัติของเมทริกซ์ที่ว่า E^-1 - E = I เมื่อ E^-1 คือเมทริกซ์ผกผันของเมทริกซ์เข้ารหัส E จึงสรุปได้ว่า 1. ผู้รับสารจะต้องทราบเมทริกซ์เข้ารหัส E เพื่อใช้ในการถอดรหัส 2. เมทริกซ์เข้ารหัส E จะต้องเป็นเมทริกซ์ที่มีเมทริกซ์ผกผัน กล่าวคือ เมทริกซ์เข้ารหัส E มีขนาด และมีเมทริกซ์ผกผันเมื่อ m x m คือ m จำนวนแถวของเมทริกซ์ข้อความ M

เมื่อผู้รับสารได้รับเมทริกซ์ผลลัพธ์ X ผู้รับสารจะต้องทำการถอดรหัสอย่างไรเพื่อให้ได้ข้อความที่ผู้ส่งสารส่งมา

   จะเห็นว่า หากเมทริกซ์เข้ารหัส E มีเมทริกซ์ผกผัน เมื่อนำเมทริกซ์ผกผันของเมทริกซ์เข้ารหัส E มาคูณกับเมทริกซ์ผลลัพธ์ X ผลคูณที่จะได้คือเมทริกซ์ข้อความ M ซึ่งเป็นไปตามสมบัติของเมทริกซ์ที่ว่า E^-1 - E = I เมื่อ E^-1 คือเมทริกซ์ผกผันของเมทริกซ์เข้ารหัส E จึงสรุปได้ว่า

   1. ผู้รับสารจะต้องทราบเมทริกซ์เข้ารหัส E เพื่อใช้ในการถอดรหัส

   2. เมทริกซ์เข้ารหัส E จะต้องเป็นเมทริกซ์ที่มีเมทริกซ์ผกผัน กล่าวคือ เมทริกซ์เข้ารหัส E มีขนาด m x m และมีเมทริกซ์ผกผัน เมื่อ m คือ จำนวนแถวของเมทริกซ์ข้อความ M

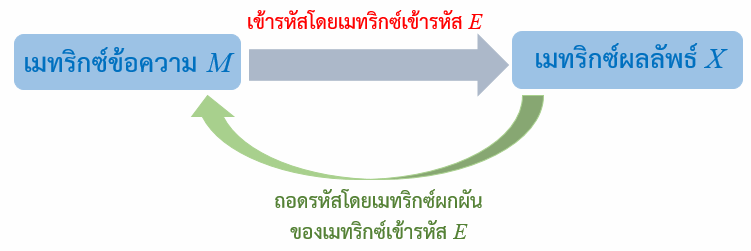
แผนภาพแสดงขั้นตอนของการเข้ารหัสและถอดรหัสโดยใช้เมทริกซ์

      หลังจากที่ผู้รับสารถอดรหัสได้เป็นเมทริกซ์ข้อความ M แล้ว ผู้รับสารจะต้องสร้างชุดลำดับของจำนวนจากเมทริกซ์ข้อความ M จากนั้นแปลงชุดลำดับของจำนวนตามระบบ Unicode ไปเป็นข้อความ

      จากที่กล่าวมาทั้งหมดสามารถสรุปเป็นขั้นตอนวิธีการรักษาความปลอดภัยของข้อมูลโดยใช้เมทริกซ์ ได้ดังนี้

      ผู้ส่งสาร

      1. แปลงข้อความที่ต้องการสื่อสารให้เป็นชุดลำดับของจำนวนตามระบบ Unicode

      2. สร้างเมทริกซ์ข้อความ M

      3. สร้างเมทริกซ์เข้ารหัส E ที่มีเมทริกซ์ผกผัน

      4. เข้ารหัส โดยหาเมทริกซ์ผลลัพธ์ X จากการนำเมทริกซ์เข้ารหัส E คูณกับเมทริกซ์ข้อความ M

      ผู้รับสาร

      1. ถอดรหัส โดยหาเมทริกซ์ข้อความ M จากการนำเมทริกซ์ผกผันของเมทริกซ์เข้ารหัส E คูณกับเมทริกซ์ผลลัพธ์ X

      2. สร้างชุดลำดับของจำนวนจากเมทริกซ์ข้อความ M

      3. แปลงชุดลำดับของจำนวนตามระบบ Unicode ไปเป็นข้อความ

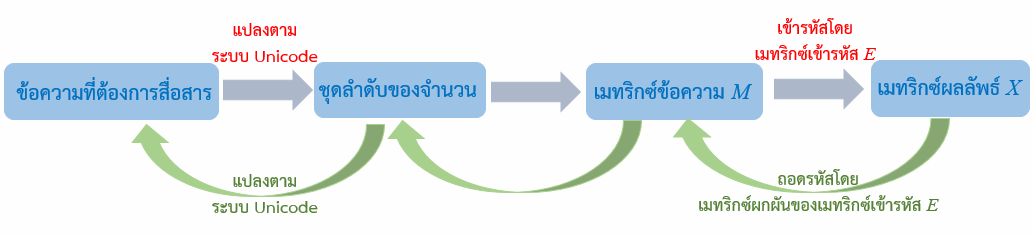
แผนภาพแสดงขั้นตอนวิธีการรักษาความปลอดภัยของข้อมูลโดยใช้เมทริกซ์

   จากขั้นตอนวิธีการรักษาความปลอดภัยของข้อมูลโดยใช้เมทริกซ์ พบว่าสามารถประยุกต์ใช้โปรแกรมสำเร็จรูป GeoGebra มาช่วยในขั้นตอนต่าง ๆ ได้ โดยมีคำสั่งสำคัญดังนี้

   • คำสั่ง TextToUnicode( <Text> ) สำหรับสร้างชุดลำดับของจำนวนจากข้อความ ตามระบบ Unicode

   • คำสั่ง C*D สำหรับหาผลคูณของเมทริกซ์ C และเมทริกซ์ D

   • คำสั่ง Invert( <Matrix> ) สำหรับหาเมทริกซ์ผกผัน

   • คำสั่ง UnicodeToText( <List of Integers> ) สำหรับแปลงชุดลำดับของจำนวนเป็นข้อความตามระบบ Unicode

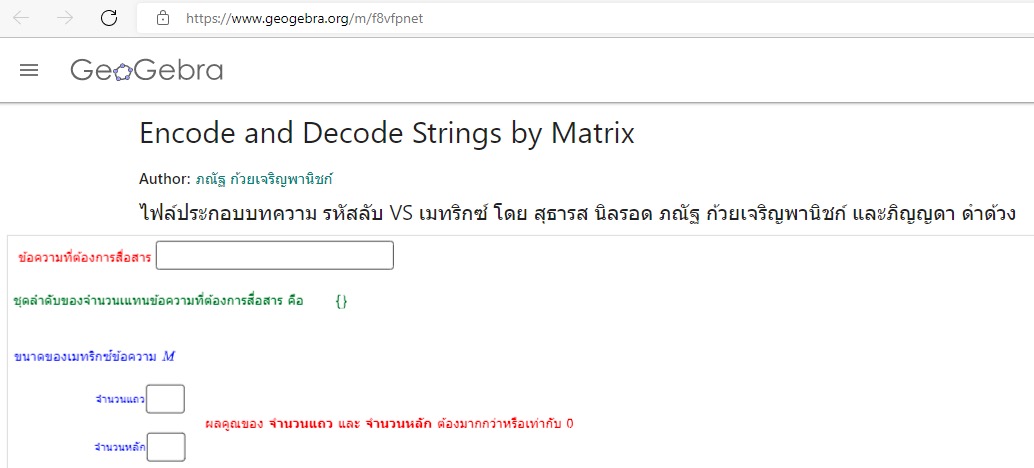
ภาพแสดงหน้าจอสื่อการเรียนรู้ Encode and Decode Strings by Matrix

   ทั้งนี้ สามารถทดลองใช้สื่อการเรียนรู้ Encode and Decode Strings by Matrix ได้ที่ https://www.geogebra.org/m/f8vfpnet โดยมีขั้นตอนดังนี้ (หมายเหตุ : เมทริกซ์สามารถเขียนภายใต้วงเล็บ ( ) หรือ [ ] ได้)

   1. พิมพ์ข้อความที่ต้องการสื่อสาร ลงในช่องข้อความที่ต้องการสื่อสาร เช่น

      โปรแกรมจะสร้างชุดลำดับของจำนวนแทนข้อความที่ต้องการสื่อสาร ดังนี้

   2. กำหนดขนาดของเมทริกซ์ข้อความ M โดยระบุจำนวนแถวและจำนวนหลัก ซึ่งผลคูณของจำนวนแถวและจำนวนหลักต้องมากกว่าหรือเท่ากับจำนวนสมาชิกของชุดลำดับของจำนวน และโปรแกรมจะสร้างเมทริกซ์ข้อความ M ตามขนาดที่กำหนด (หมายเหตุ Unicode 32 คือ ช่องว่าง)

   3. บันทึกสมาชิกของเมทริกซ์เข้ารหัส E โดยต้องบันทึกสมาชิกทีละแถวตามที่ปรากฏ ทั้งนี้ โปรแกรมจะทำการตรวจสอบว่าเมทริกซ์เข้ารหัส E ที่สร้างสอดคล้องกับเงื่อนไขหรือไม่ หากไม่สอดคล้อง จะขึ้นข้อความ “เมทริกซ์เข้ารหัสไม่สอดคล้องเงื่อนไข”จะต้องแก้ไขสมาชิกในเมทริกซ์เข้ารหัส E ให้สอดคล้องกับเงื่อนไข

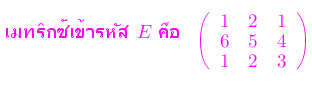
กรณีเมทริกซ์เข้ารหัส E ที่สอดคล้องกับเงื่อนไข

กรณีเมทริกซ์เข้ารหัส E ที่ไม่สอดคล้องกับเงื่อนไข

   4. โปรแกรมจะทำการเข้ารหัสเมทริกซ์ข้อความ M และแสดงขั้นตอนการเข้ารหัสและถอดรหัสข้อความ

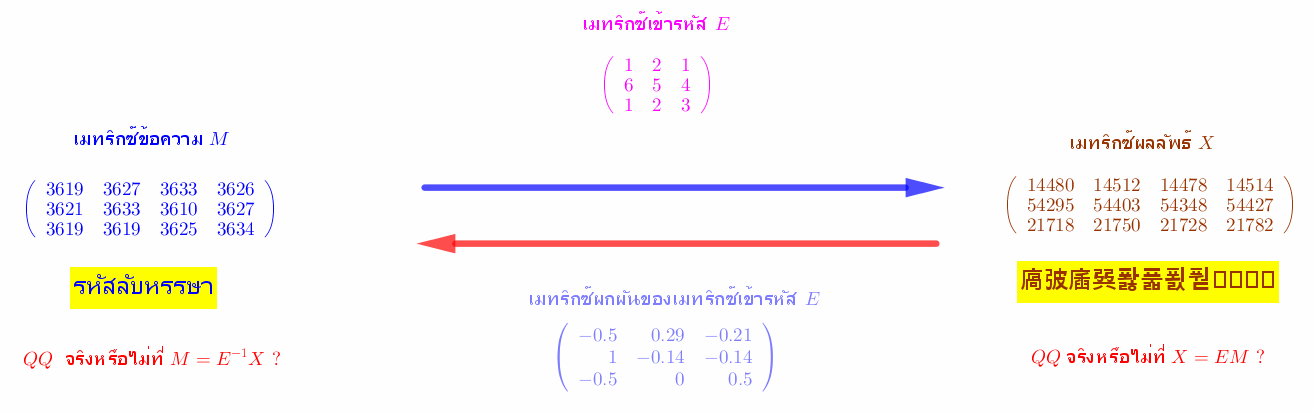
หมายเหตุ : ข้อความ    เกิดจากการแปลงชุดลำดับของจำนวนที่เป็นสมาชิกของเมทริกซ์ผลลัพธ์ X

บทความนี้เป็นส่วนหนึ่งของนิตยสาร สสวท. ปีที่ 50 ฉบับที่ 237 กรกฎาคม - สิงหาคม 2565

ผู้อ่านสามารถติดตามบทความที่น่าสนใจเพิ่มเติมได้ที่ https://emagazine.ipst.ac.th/

บรรณานุกรม

Wikipedia, the free encyclopedia. Claude Shannon. สืบค้นเมื่อ 5 สิงหาคม 2565. จาก https://en.wikipedia.org/wiki/Claude_Shannon.Wikipedia, the free encyclopedia. Claude Shannon. สืบค้นเมื่อ 5 สิงหาคม 2565. จาก https://en.wikipedia.org/wiki/Claude_Shannon.

สถาบันนวัตกรรมการเรียนรู้ มหาวิทยาลัยมหิดล. Claude Shannon. สืบค้นเมื่อ 5 สิงหาคม 2565. จาก https://il.mahidol.ac.th/e-media/computer/evolution/sw_1948.htm.

สถาบันส่งเสริมการสอนวิทยาศาสตร์และเทคโนโลยี. (2563). หนังสือเรียนรายวิชาเพิ่มเติมคณิตศาสตร์ชั้นมัธยมศึกษาปีที่ 5 เล่ม 1 ตามมาตรฐานการเรียนรู้และตัวชี้วัดกลุ่มสาระการเรียนรู้คณิตศาสตร์ (ฉบับปรับปรุง พ.ศ.2560) ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551. พิมพ์ครั้งที่ 2. กรุงเทพมหานคร:สำนักพิมพ์จุฬาลงกรณ์มหาวิทยาลัย.