คณิตศาสตร์เป็นสิ่งที่พบได้รอบตัวในชีวิตประจำวัน เช่น การดำเนินการของจำนวนที่นำไปใช้ได้กับหลากหลายสถานการณ์  ตั้งแต่การคำนวณราคาค่าสินค้าหรือจำนวนเงินทอน จนถึงการนำไปใช้ในระดับที่ซับซ้อน เช่น การวิเคราะห์เชิงตัวเลข เรขาคณิตที่นำไปใช้ในการออกแบบผลิตภัณฑ์  บรรจุภัณฑ์  สถาปัตยกรรม ฯลฯ หรือสถิติที่นำไปใช้วิเคราะห์ข้อมูลจากหน้าสื่อสิ่งพิมพ์  ตลอดจนใช้คาดการณ์ดูแนวโน้มของข้อมูลที่สนใจศึกษา

  เนื้อหาคณิตศาสตร์บางเรื่องที่มีความซับซ้อนขึ้นอาจทำให้หลายคนเกิดคำถามขึ้นว่า แนวคิดทางคณิตศาสตร์ที่เป็นนามธรรมเหล่านั้น สามารถนำไปใช้ในชีวิตจริงได้หรือไม่ ในบทความนี้จะขอกล่าวถึงตัวอย่างของการนำคณิตศาสตร์ที่เป็นนามธรรมไปใช้ประโยชน์ในวิทยาการเข้ารหัสลับวิทยาการเข้ารหัสลับ เป็นการศึกษาวิธีการรักษาความปลอดภัยของข้อมูล ในการสื่อสารระหว่างสองฝ่ายโดยไม่ให้บุคคลอื่นล่วงรู้ด้วยการเข้ารหัส ซึ่งก็คือการแปลงข้อความที่ต้องการสื่อสารเป็นข้อความใหม่ หรือที่เรียกว่า ข้อความที่ถูกเข้ารหัส วิธีการเข้ารหัสจะรู้เฉพาะผู้ส่งสารและผู้รับสาร ทำให้ผู้รับสารสามารถถอดรหัสหรือแปลงข้อความที่ถูกเข้ารหัสกลับไปเป็นข้อความดั้งเดิมได้เนื่องจากบุคคลอื่นไม่รู้วิธีการเข้ารหัส จึงไม่สามารถเข้าใจข้อความนั้นได้ ทำให้ข้อมูลที่ต้องการสื่อสารปลอดภัย

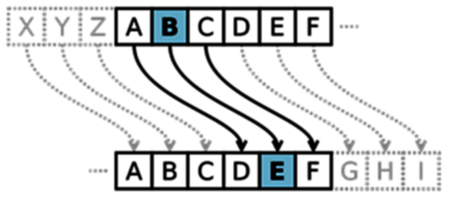
   หากมองย้อนไปในประวัติศาสตร์วิทยาการเข้ารหัสลับได้เกิดขึ้นมาหลายพันปีแล้ว และถูกนำไปใช้ในวงการต่าง ๆ เช่นทางการทหาร จูเลียส ซีซาร์  ได้ใช้วิธีการเข้ารหัส ที่รู้จักกันในนาม “รหัสซีซาร์” โดยใช้การแปลงข้อความที่ต้องการส่ง ด้วยการแทนที่ตัวอักษรในตำแหน่งที่กำหนดไว้ เพื่อปกป้องข้อมูลลับ เช่น การกำหนดให้แทนที่ตัวอักษรในตำแหน่งเดิมด้วยตัวอักษรที่ได้ จากการเลื่อนไป 3 ตำแหน่ง ดังนี้  

           A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

      แทนด้วย

           D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

       ตามลำดับ

ภาพที่ 1 จูเลียส ซีซาร์  กับรหัสซีซาร์
ที่มา : http ://en.wikipedia.org/wiki/Julius_Caesar  และ http://ritajeanmoran.blogspot.com/2012/08/codes-and-ciphers.html

   ดังนั้น ถ้าข้อความที่ต้องการส่ง คือ MATHEMATICS IS FUN เมื่อเข้ารหัสซีซาร์  จะได้ข้อความใหม่เป็น PDWLHPDWLFV LVIXQ ซึ่งผู้ที่ทราบวิธีการเข้ารหัส จะสามารถแปลงข้อความกลับไปเป็นข้อความเดิมได้โดยง่าย แต่ผู้ที่ไม่ทราบวิธีการเข้ารหัสจะไม่สามารถเข้าใจข้อความดังกล่าวได้ด้วยเวลาอันรวดเร็ว

   ลองพิจารณาตัวอย่างสถานการณ์พื้นฐานที่ใช้อ้างถึงบ่อยครั้งเพื่ออธิบายเกี่ยวกับการรักษาความปลอดภัยของข้อมูล ดังต่อไปนี้

สถานการณ์

   อลิซต้องการส่งของบางอย่างที่เป็นความลับให้บ็อบ โดยนำของนั้นใส่กระเป๋าใบหนึ่ง และให้ชาร์ลีเป็นคนกลางในการส่งต่อกระเป๋า อลิซมีแม่กุญแจและลูกกุญแจหนึ่งชุด ในขณะเดียวกัน  บ็อบก็มีแม่กุญแจและลูกกุญแจอีกหนึ่งชุด ซึ่งเป็นคนละชุดกับอลิซ ทำให้ไม่สามารถใช้ไขเพื่อปลดล็อกกุญแจของอลิซได้

คำถาม

   จะต้องทำอย่างไร อลิซจึงจะส่งกระเป๋าใบดังกล่าวให้บ็อบ และบ็อบสามารถเปิดกระเป๋าเพื่อนำสิ่งของข้างในออกมาได้ โดยชาร์ลีไม่สามารถเปิดกระเป๋าเพื่อดูสิ่งของที่อยู่ข้างในได้ ในขณะที่กระเป๋าอยู่ในมือเขา

ขั้นตอนการแก้ปัญหา

   1. อลิซล็อกกุญแจกระเป๋าด้วยกุญแจของตนเองโดยเก็บลูกกุญแจไว้ แล้วฝากชาร์ลีนำกระเป๋าไปให้บ็อบ

   2. เมื่อบ็อบได้รับกระเป๋า บ็อบล็อกกุญแจกระเป๋าด้วยกุญแจของตนเองโดยเก็บลูกกุญแจไว้ แล้วฝากชาร์ลีนำกระเป๋าไปให้อลิซจะสังเกตว่าตอนนี้กระเป๋าถูกล็อกด้วยกุญแจสองชุด

   3. เมื่ออลิซได้รับกระเป๋า อลิซปลดล็อกกุญแจของตนเองออกแล้วฝากชาร์ลีนำกระเป๋าไปให้บ็อบ

   4. เมื่อบ็อบได้รับกระเป๋าที่ล็อกด้วยกุญแจของตนเอง บ็อบจึงสามารถเปิดกระเป๋าได้ในที่สุด

   จากขั้นตอนดังกล่าว จะเห็นว่าชาร์ลีไม่สามารถเปิดกระเป๋าได้เลย เนื่องจากกระเป๋าถูกล็อกอยู่ตลอด ในระหว่างที่อยู่ในมือชาร์ลี

   สถานการณ์ข้างต้นคล้ายคลึงกับระบบการส่งข้อมูลแบบดิจิทัล ซึ่งเป็นระบบที่ใช้ติดต่อสื่อสารระหว่างเครื่องคอมพิวเตอร์ สามารถอธิบายได้โดยให้ชาร์ลีเป็นตัวแทนระบบอิเล็กทรอนิกส์ที่ใช้ส่งต่อข้อมูล กระเป๋าเป็นตัวแทนของข้อมูลที่อยู่ในรูปเลขฐานสอง กุญแจของอลิซและบ็อบเป็นตัวแทนของจำนวนที่เป็นเลขฐานสองและการดำเนินการของเลขฐานสอง

ภาพที่ 2 การส่งข้อมูลในรูปเลขฐานสอง
ที่มา : http ://eandt.theiet.org/news/2013/sep/quantum-cryptography.cfm

ตัวอย่างเช่น กำหนดให้

   กระเป๋า แทนด้วย 0011 ซึ่งเป็นเลขฐานสอง

   การล็อกกุญแจของอลิซ แทนด้วย การบวกเลขฐานสองด้วย 0101 ซึ่งเป็นเลขฐานสอง

   และการล็อกกุญแจของบ็อบ แทนด้วย การบวกเลขฐานสองด้วย 0110 ซึ่งเป็นเลขฐานสอง

   ดังนั้น การปลดล็อกกุญแจของอลิซ ก็คือการลบเลขฐานสองด้วย 0101

   และการปลดล็อกกุญแจของบ็อบ ก็คือการลบเลขฐานสองด้วย 0110

   เมื่ออลิซล็อกกุญแจกระเป๋า ซึ่งก็คือการบวกข้อมูลตั้งต้น 0011 ด้วย 0101 จะได้ข้อมูลใหม่เป็น 1000 เมื่อบ็อบล็อกกุญแจกระเป๋าเพิ่มไปอีกชุด ซึ่งก็คือการบวกข้อมูล 1000 ด้วย 0110 จะได้ข้อมูลใหม่เป็น 1110 เขียนแสดงโดยแผนภาพได้ดังนี้

   เมื่ออลิซปลดล็อกกุญแจของตนเองออก ซึ่งก็คือการลบข้อมูล 1110 ด้วย 0101 จะได้ข้อมูลใหม่เป็น 1001 เมื่อบ็อบปลดล็อกกุญแจของตนเองออก ซึ่งก็คือการลบข้อมูล 1001 ด้วย 0110 จะได้ข้อมูลใหม่เป็น 0011 เขียนแสดงโดยแผนภาพได้ดังนี้

   ซึ่งผลลัพธ์ที่ได้ก็คือข้อมูลตั้งต้นนั่นเอง ทั้งนี้ หากไม่ทราบวิธีการเข้ารหัส ซึ่งเปรียบได้กับการล็อกกุญแจของอลิซและบ็อบ ก็จะไม่สามารถทราบข้อมูลตั้งต้นได้

   จากตัวอย่างจะเห็นได้ว่าการแปลงสถานการณ์จริงให้อยู่ในรูปข้อมูลเชิงคณิตศาสตร์  ทำให้สามารถใช้เครื่องมือและทฤษฎีทางคณิตศาสตร์มาช่วยในการแก้ปัญหาได้ ซึ่งเป็นประโยชน์แก่การพัฒนาวิทยาการเข้ารหัสลับ เกื้อหนุนให้วิทยาการเข้ารหัสลับถูกพัฒนาไปอย่างรวดเร็ว

   ตัวอย่างของวิทยาการเข้ารหัสลับในชีวิตประจำวันที่ใช้แพร่หลายอีกอย่างหนึ่งคือ บัตรกดเงินสดหรือบัตรเอทีเอ็ม ซึ่งในตัวบัตรจะมีไมโครชิปที่ใช้เก็บข้อมูลของผู้ถือบัตร โดยผู้ถือบัตรจะได้รับรหัส PIN เป็นตัวเลขสี่หลักที่ถูกส่งให้แยกกับตัวบัตรพร้อมคำแนะนำ ว่าให้ผู้ถือบัตรจำรหัส PIN นี้ไว้ และระวังไม่ให้ผู้อื่นล่วงรู้ได้ เพราะแม้แต่ธนาคารที่ออกบัตรก็ไม่ทราบรหัส PIN ของลูกค้าเนื่องจากรหัส PIN หรือ Personal Identification Number ใช้ในการยืนยันความเป็นผู้ถือบัตร เมื่อเสียบบัตรเข้าไปในเครื่องรับจ่ายเงินอัตโนมัติหรือตู้เอทีเอ็มแต่ละครั้ง เครื่องจะขอให้ป้อนรหัส PIN หากป้อนรหัสได้ถูกต้อง เครื่องจึงจะทำงานต่อได้ ซึ่งสามารถอธิบายหลักการทำงานของบัตร เอทีเอ็ม และรหัส PIN อย่างย่อได้ดังนี้

ภาพที่ 3 ตู้เอทีเอ็ม
ที่มา : http ://www.infolanka.com/news/IL/1150.htm

   เมื่อเสียบบัตรเข้าไปในตู้เอทีเอ็ม ระบบของธนาคารจะถามคำถามเพื่อให้ยืนยันความเป็นผู้ถือบัตรที่แท้จริง โดยคำถามจะแตกต่างกันในแต่ละครั้งและคำถามเหล่านี้จะถูกสุ่มในรูปของตัวเลข จากนั้นไมโครชิปในตัวบัตรจะทำหน้าที่คำนวณโดยใช้ตัวเลขจากคำถามที่ธนาคารส่งมาร่วมกับรหัส PIN ที่ผู้ถือบัตรป้อนเข้าไป แล้วระบบจะส่งข้อมูลซึ่งคือผลลัพธ์ที่ได้จากการคำนวณกลับไปยังธนาคาร ซึ่งจากข้อมูลนี้เอง จะทำให้ธนาคารรู้ได้ว่าบุคคลนั้น  เป็นผู้ถือบัตรที่แท้จริงหรือไม่ โดยที่ธนาคารไม่จำเป็นต้องรู้รหัส PIN ของผู้ถือบัตร ซึ่งการคำนวณที่อยู่เบื้องหลังการทำงานของบัตรเอทีเอ็มใช้หลักการของเลขยกกำลัง จำนวนเฉพาะ ความรู้ด้านพีชคณิต และทฤษฎีจำนวนขั้นสูง

   แม้ว่านักคณิตศาสตร์ในอดีต ผู้ค้นคว้าวิจัยเกี่ยวกับจำนวนเฉพาะ อาจไม่ได้คำนึงถึงการนำจำนวนเฉพาะไปประยุกต์ใช้ในวิทยาการเข้ารหัสลับ แต่หากไม่มีงานวิจัยของนักคณิตศาสตร์เหล่านั้น เราก็อาจไม่มีบัตรเอทีเอ็ม ใช้ในปัจจุบันก็เป็นได้ ดังนั้น แม้คณิตศาสตร์บริสุทธิ์จะมีต้นกำเนิดจากความสนใจใคร่รู้ทางทฤษฎี ที่อาจจะดูเหมือนไม่มีความสัมพันธ์กับการนำไปใช้ในชีวิตจริง จนหลายคนอาจมองว่างานวิจัยเหล่านี้ไม่มีประโยชน์  แต่ความรู้ทางคณิตศาสตร์บริสุทธิ์นี่เองที่เป็นรากฐานที่สำคัญ เป็นจุดกำเนิดของการพัฒนาศาสตร์หลาย ๆ ด้านในเวลาต่อมา ที่เราอาจคาดไม่ถึง ดัง G. H.Hardy ( พ.ศ. 2420 -  พ.ศ. 2490 ) นักคณิตศาสตร์ชาวอังกฤษที่เชี่ยวชาญด้านทฤษฎีจำนวน เคยเขียนไว้ในหนังสือชื่อ The Mathematician’ s Apology  ว่า “I have never done anything “useful” . No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world. ... Judged by all practical standards, the value of my mathematical life is nil.” หรือแปลเป็นภาษาไทยได้ว่า “ข้าพเจ้าไม่เคยทำสิ่งที่ “มีประโยชน์” สิ่งที่ข้าพเจ้าค้นพบไม่เคยสร้างหรือเกือบจะสร้างความแตกต่างที่จะนำไปสู่สิ่งอำนวยความสะดวกใด ๆ ในโลกใบนี้ ทั้งทางตรงหรือทางอ้อม ทั้งทางดีหรือทางร้าย... ประเมินจากมาตรฐานในทางปฏิบัติแล้ว คุณค่าของชีวิตนักคณิตศาสตร์ ของข้าพเจ้านั้นมีค่าเป็นศูนย์”งานวิจัยของ Hardy อาจจะถูกมองว่า “ไม่มีประโยชน์” ในเวลานั้น แต่บัดนี้เวลาได้พิสูจน์แล้วว่าการค้นคว้าวิจัยเกี่ยวกับจำนวนเฉพาะของเขา เป็นพื้นฐานที่จำเป็นและมีคุณค่ายิ่งสำหรับวิทยาการเข้ารหัสลับและวิทยาการอื่น ๆ อีกมากมายในปัจจุบัน

ภาพที่ 4 G. H. Hardy
ที่มา : http ://en.wikipedia.org/wiki/G._H._Hardy

บรรณานุกรม

Jean-Louis Nicolas. Cryptage et décryptage: communiqueren toute sécurité. “L’explosion des Mathématiques”, SMF-SMAI, Paris, July 2002, 15-18.

M. Waldschmidt. Arithmetic and Cryptography. Resonance, May 2008, 13(1), 440-455.

M. Waldschmidt. Cryptographie: une introduction élémentaire. บทความประกอบการบรรยายที่ Maths-Club

de l’IREM, Université Paris Diderot ประเทศฝรั่งเศส วันที่ 26 ตุลาคม 2552 และ Université des Sciences et de la Technologie Houari-Boumediène (USTHB) ประเทศแอลจีเรีย วันที่ 8 มิถุนายน 2552, จาก http://www.math.jussieu.fr/~miw/articles/pdf/Cryptographie2009VI.pdf

M. Waldschmidt. Les codes secrets et l’arithmétique.สืบค้นเมื่อ 21 พฤษภาคม 2557 จาก http://www.math.jussieu.fr/~miw/articles/pdf/ArithmetiqueCryptographie.pdf