ถ้าเราเป็นมนุษย์ในยุคโบราณที่ไม่มีเครื่องมือหรือเทคโนโลยีที่ใช้คำนวณว่า เรือลำนั้นที่อยู่กลางทะเลห่างจากฝั่งและตัวเราระยะทางเท่าไร เคยสงสัยกับคำถามนี้หรือไม่ อยากรู้หรือไม่ 

ภาพที่ 1 การเดินทางของเรือในท้องทะเล
ที่มา Pixabay

         หากปัจจุบันเราคงไม่ข้องใจว่าเทคโนโลยีที่ช่วยในการเดินทาง ทั้งทางเรือ ทางบก ทางอากาศ ต่างก็มี GPS ที่ช่วยในการคำนวณการเดินทางอย่างแม่นยำ

         ในยุคกรีกโบราณ มีนักวิทยาศาสตร์และคณิตศาสตร์ชื่อว่า เธลีส ซึ่งมีประวัติการกล่าวถึงเกี่ยวกับการเขียนตำราการหาทิศและการเดินเรือ เธลีสเป็นผู้ที่มีชื่อเสียงและความสามารถคนหนึ่งในประวัติศาสตร์การคำนวณเพื่อพยากรณ์การเกิดสุริยุปราคาในอดีตได้อย่างแม่นยำ และเป็นนักเดินทางเพื่อแสวงหาคำตอบในธรรมชาติ รวมถึงศาสตร์ของการเดินเรือ

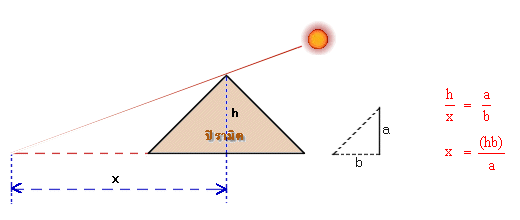
ภาพที่ 2 วิธีการคำนวณความสูงของปิรามิดที่อียิปต์
ที่มา https://web.ku.ac.th/schoolnet/snet2/mathematicians/thales.htm

         เธลีส ได้มีโอกาสดินทางไปประอิยิปต์ในช่วงที่ศาสตร์ทางด้านคณิตศาสตร์กำลังรุ่งเรือง  เธลีสได้คิดและเสนอหลักการเกี่ยวกับการคำนวณด้านเรขาคณิต โดยเสนอวิธีคำนวณหาความสูงของปิรามิดที่อียิปต์ โดยการวัดระยะทางของเงาที่เกิดขึ้นที่ฐานของปิรามิด กับเงาของหลักที่รู้ความสูงแน่นอน หลักการดังกล่าว เป็นลักษณะที่เราคุ้นเคยคือ การใช้รูปสามเหลี่ยมคล้าย  และนั่นก็เป็นจุดเริ่มต้นหนึ่งของศาสตร์การเดินเรือที่สำคัญ

        ในยุคที่มีใช้เข็มทิศแม่เหล็ก เครื่องวัดดาว และนาฬิกาโครโนเมตร กับความรู้ทางด้านดาราศาสตร์และแผนที่ในสมัยนั้นเพียงเท่านั้น เราเรียกวิธีการหาตำแหน่งและทิศทางในสมัยนี้ว่า การเดินเรือรายงานและเดินเรือชายฝั่ง ซึ่งเป็นเพียงแค่การคาดคะเนเพียงเท่านั้น จากความเร็วและเวลา รวมถึงกระแสลม   ยุคศตวรรษที่ 12 ความรู้เรื่องการใช้เข็มทิศแม่เหล็กมีวิวัฒนาการที่ดีขึ้น โดยการใช้การโยนวัตถุลอยน้ำ และพัฒนามาเป็นการโยนท่อนไม้ที่ผูกเชือกเป็นปมลง ท้ายเรือ และนับจำนวนปมเชือกที่ปล่อยออกไปขณะใช้นาฬิกาทรายจับเวลา ซึ่งวิธีนี้เป็นที่มาของ การนับหน่วยความเร็วเรือเป็นนอต (knot – ปมเชือก)

        ในยุคที่ดาราศาสตร์เฟื่องฟู การเดินเรือดาราศาสตร์โดยความรู้ทางด้านดาราศาสตร์และคณิตศาสตร์กลายเป็นเครื่องสำคัญ ประกอบกับเครื่องมือที่พัฒนาสำหรับเดินเรือ ทำให้มีการเดินทางเพื่อสำรวจโลก จากนักเดินทางมากมาย

        ในวิชาการเดินเรือภาคปัจจุบัน ก็มีการนำเอาความรู้เกี่ยวกับสามเหลี่ยมนี้มาใช้ในการคำนวณหาตำบลที่เรือ ซึ่งเป็นที่รู้กันในหมู่นักการเดินเรือและทหารเรือว่า ตำบลที่เรือ ก็คือ ละติจูด ลองจิจูด การหาตำบลที่เรือมีวิธีต่าง ๆ มากมาย ซึ่งแล้วแต่อุปกรณ์ในการที่มีอยู่ในบนเรือชนิดต่าง ๆ แต่สิ่งสำคัญที่สุดคือแผนที่ ซึ่งมีมาตราส่วนสำคัญ และเลขละติจูด ลองจิจูด ที่ทำให้เราสามารคำนวณและหาทิศทางของเรือนั้นได้

        ก่อนหน้านี้เราคำนวณหาตำบลที่เรือด้วยวิธีการพล๊อตตำแหน่งจากดาวเทียม และต่อมาก็มีการใช้การคำนวณทางคณิตศาสตร์ โดยสูตรที่ใช้ก็เป็นเพียงสูตรคณิตศาสตร์พื้นฐานเกี่ยวกับ ทฤษฎีบทของปีทาโกรัส (Pythagoras) หรือทฤษฎีสามเหลี่ยมมุมฉากว่า “ในรูปสามเหลี่ยมมุม ฉากใด ๆ กําลังสองของความยาวของด้านตรงข้ามมุมฉาก (c) เท่ากับผลบวกของกําลังสองของความ ยาวด้านประกอบมุมฉาก (a, b)”

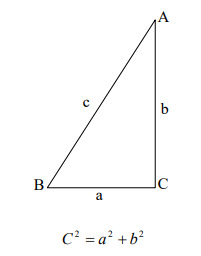
ภาพที่ 3 ทฤษฎีสามเหลี่ยมมุมฉาก
ที่มา http://library.rtna.ac.th/web/RTNA_Journal/y.9c.4/02.pdf

ตัวอย่างจริงการคำนวณหาระยะทางจากเรือประมงไปเกาะโลซิน ตามวิธีทางคณิตศาสตร์อย่างง่าย โดยดูภาพประกอบ

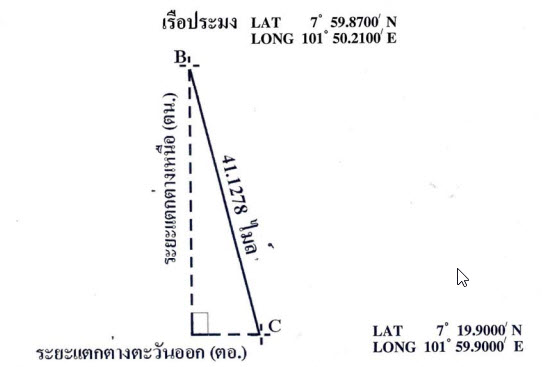
ภาพที่ 4 ภาพการคำนวณหาระยะทางจากเรือประมงไปเกาะโลซิน

        หาตำแหน่งระยะทางจากเรือประมงไปยัง เกาะโลซิน ซึ่งเรียกว่า ระยะแตกต่างเหนือ (ตน.)

        จากภาพที่เราทราบ

             ตำแหน่งตำบลที่เรือ (ตน.)   = 7 ° 59.8700 ' -    7 ° 19.9000 ' = 0 ° 39.9700 '

             ตำแหน่งตำบลที่เรือ (ตอ.)   = 10 ° 59.900 ' -    101 ° 50.2100 ' = 0 ° 09.6900 '

             ทฤษฎีบทของปีทาโกรัส (Pythagoras)   สามเหลี่ยมมุมฉาก   BC² = (ตน.)² + (ตอ.)²      

             แทนค่า   BC² = 39.9700² + 09.6900²

                           BC² = 1597.6009 + 93.8961

                           BC² = 1691.4970

                           BC  = รากที่ 2 ของ 1691.4970 = 41.1278

                          ดังนั้น ระยะทางจากเรือประมง ไปเกาะโลซินเท่ากับ 41.1278 ไมล์ (1 องศา = 60 ไมล์ หรือ 1 ลิปดา = 1 ไมล์)

       อย่างไรก็ตาม การคำนวณดังกล่าว เป็นการคำนวณแนวราบ แต่พื้นที่โลกจริงซึ่งมีลักษณะโค้ง ต้องอาศัยการคำนวณเพิ่มที่มีความละเอียดมากกว่านี้ โดยคำนวณระยัลงสู้พื้นราบประกอบด้วย

แหล่งที่มา

น.อ.วินัย มณีพฤกษ์ .   การคำนวณหาตำบลที่เรือด้วยวิธีทางคณิตศาสตร์.  สืบค้นเมื่อ 8 ธันวาคม 2560, จาก
        http://library.rtna.ac.th/web/RTNA_Journal/y.9c.4/02.pdf

ศิลป์และศาสตร์แห่งการเดินเรือ – จากที่เรือรายงานสู่ที่เรือดาวเทียม (ตอนที่ ๑)เธลิส.  สืบค้นเมื่อ 8 ธันวาคม 2560, จาก
        https://kapitaennem0.wordpress.com/oldposts/nav1/

_{รศ. ยืน ภู่วรวรรณ สำนักบริการคอมพิวเตอร์ มหาวิทยาลัยเกษตรศาสตร์} .   เธลิส.  สืบค้นเมื่อ 8 ธันวาคม 2560, จาก
        https://web.ku.ac.th/schoolnet/snet2/mathematicians/thales.htm