บทเรียนที่ 1 แบบจำลองอะตอมของดอลตัน

โมเลกุลของสารมีขนาดเล็กมาก ไม่สามารถมองเห็นได้ด้วยตาเปล่าและโมเลกุลของก๊าซบางชนิด เช่น ก๊าซไฮโดรเจน ออกซิเจน ไนโตรเจน ก็ประกอบด้วย 2 อะตอม แสดงว่าอะตอมน่าจะมีขนาดเล็กกว่าโมเลกุล การที่จะศึกษาว่าอะตอมมีลักษณะอย่างไร ภายในอะตอมมีอนุภาคใดเป็นองค์ประกอบและอนุภาคเหล่านั้นมีสมบัติเป็นอย่างไรจึงเป็นเรื่องที่ทำได้จึงเป็นเรื่องที่ทำได้ยากแต่นักวิทยาศาสตร์ก็ใช้วิธีการต่างๆ เพื่อศึกษาหาคำตอบในเรื่องดังกล่าว ในบทนี้นักเรียนจะได้ศึกษาว่านักวิทยาศาสตร์ใช้วิธีการใด เพื่อให้ได้ข้อมูลเกี่ยวกับอะตอม และจากข้อมูลนั้นใช้อธิบายโครงสร้างอะตอมได้อย่างไร รวมถึงการนำความรู้เรื่องโครงสร้างอะตอมไปใช้อธิบายปรากฏการณ์บางอย่างที่เกิดขึ้นได้

อะตอมมาจากภาษากรีกว่า “atomos” ซึ่งแปลว่า “แบ่งแยกอีกไม่ได้” หมายความว่า อะตอม คือ หน่วยย่อยที่เล็กที่สุดซึ่งไม่สามารถแบ่งให้เล็กลงไปได้อีก แนวความคิดดังกล่าวนี้ได้จากนักปราชญ์ชาวกรีก ชื่อ ดิโมคริตุส(Demokritos)

เนื่องจากอะตอมมีขนาดเล็กมากจึงยังไม่เคยมีใครมองเห็นด้วยตาเปล่า แม้แต่ใช้กล้องจุลทรรศน์อิเล็กตรอน ก็ยังไม่สามารถมองเห็นอะตอมได้ จนในปัจจุบันได้มีการพัฒนากล้องจุลทรรศน์สนามไอออนที่มีกำลังขยายสูงถึง 750,000 เท่าจึงสามารถถ่ายภาพปลายเข็มของธาตุรีเนียม (Rhenium) ซึ่งเชื่อกันว่าเป็นภาพของอะตอมได้ แม้ว่าจะถ่ายภาพที่เชื่อว่าเป็นอะตอมได้ แต่จากภาพถ่ายดังกล่าวก็ยังไม่สามารถบอกรายละเอียดภายในอะตอมได้

การที่อะตอมมีขนาดเล็กมากจนไม่สามารถมองเห็นได้ การศึกษาเกี่ยวกับอะตอมจึงใช้วิธีการสันนิษฐาน โดยใช้ข้อมูลต่าง ๆ ที่ได้จากการทดลอง นำมาสร้างมโนภาพหรือแบบจำลองของอะตอมขึ้นมา แบบจำลองอะตอมมีหลายแบบ แต่ละแบบได้ถูกกำหนดขึ้นมาโดยอาศัยการทดลองเป็นหลัก ในขั้นแรกมีข้อมูลเกี่ยวกับอะตอมจำนวนน้อย ลักษณะของแบบจำลองอะตอมก็เป็นอย่างหนึ่ง เมื่อมีข้อมูลเพิ่มขึ้นจนแบบจำลองนั้นไม่สามารถอธิบายข้อมูลที่ได้จากการศึกษาใหม่ ๆ ก็จำเป็นต้องมีการแก้ไขแบบจำลองอะตอม ดังนั้นแบบจำลองอะตอมจึงได้มีการพัฒนาและเปลี่ยนแปลงไปได้เรื่อย ๆ แม้กระทั่งในปัจจุบัน

แบบจำลองคือ มโนภาพที่สร้างขึ้นโดยอาศัยข้อมูลที่ได้จากการทดลอง แบบจำลองทางวิทยาศาสตร์ เป็นมโนภาพที่นักวิทยาศาสตร์สร้างขึ้น เพื่อบอกลักษณะของสิ่งที่มองไม่เห็น เช่น อะตอม นอกจากนี้แบบจำลองยังใช้เป็นคำอธิบายสิ่งหนึ่งสิ่งใดก็ได้แบบจำลองสามารถเปลี่ยนแปลงได้เมื่อข้อมูลจากการทดลองเปลี่ยนแปลงไป

บทเรียนที่ 2 แบบจำลองอะตอมของดอลตัน

แบบจำลองอะตอมของดอลตัน

จากการที่ไม่มีผู้ใดเห็นลักษณะอะตอมด้วยตาเปล่า John Dalton นักวิทยาศาสตร์ชาวอังกฤษ ได้เสนอแนวคิดเกี่ยวกับอะตอมที่เรียกว่าทฤษฎีอะตอม ในปี ค.ศ. 1803(พ.ศ.2346) มีใจความสำคัญว่า

1. สสารทุกชนิดประกอบด้วยอนุภาคที่เล็กที่สุด ซึ่งไม่สามารถแบ่งแยกต่อไปได้อีก เรียกว่าatom

2. อะตอมของธาตุชนิดเดียวกัน ย่อมมีสมบัติเหมือนกันทุกประการ(เช่นมีมวลเท่ากัน) และมีสมบัติแตกต่างจากอะตอมของธาตุอื่น

3. ไม่สามารถทำให้อะตอมสูญหายหรือเกิดใหม่ได้ (กฎทรงมวล)

4. สารประกอบเกิดจากการรวมตัวทางเคมีระหว่างอะตอมของธาตุตั้งแต่สองชนิดขึ้นไป และจำนวนอะตอมของธาตุที่รวมตัวกันจะเป็นอัตราส่วนตัวเลขลงตัวน้อยๆ (กฎสัดส่วนคงที่)

Dalton เสนอมโนภาพของแบบจำลองอะตอมว่า อะตอมมีลักษณะทรงกลมตัน มีขนาดเล็กมาก และไม่สามารถแบ่งแยกได้อีก จากแนวคิดของดอลตันที่ว่า อะตอมเป็นหน่วยที่เล็กที่สุดซึ่งแบ่งแยกไม่ได้ ทำให้ได้แบบจำลองอะตอมของดอลตันเป็น “ทรงกลมที่มีขนาดเล็กที่สุด ซึ่งแบ่งแยกไม่ได้”

แบบจำลองอะตอมของดอลตันใช้อธิบายเกี่ยวกับกฏทรงมวลสารสัมพันธ์ได้ จึงเป็นที่ยอมรับกันในสมัยนั้น และทำให้นักวิทยาศาสตร์เริ่มหันมาสนใจศึกษาเกี่ยวกับอะตอมมากขึ้น ต่อมาเมื่อการศึกษาได้พัฒนามากขึ้น พบข้อมูลเกี่ยวกับอะตอมมากขึ้น ข้อมูลใหม่ ๆ เหล่านี้บางประการก็ไม่สอดคล้องกับแนวความคิดของดอลตัน เช่น พบว่าอะตอมไม่ใช่หน่วยที่เล็กที่สุด อะตอมยังสมารถมีอนุภาคย่อย ๆ ลงไปได้อีกก อะตอมของธาตุชนิดเดียวกันก็อาจไม่จำเป็นต้องมีสมบัติต่าง ๆ เหมือนกันทุกประการ เช่น มีมวลต่างกันได้ (คือไอโซโทป ซึ่งจะได้กล่าวในรายละเอียดต่อไป ) นอกจากนี้ข้อมูลบางเรื่องก็ไม่สามารถอธิบายได้โดยแนวความคิดของดอลตัน เช่น ปรากฏการณ์ที่เกิดขึ้นในหลอดรังสีแคโทด นักวิทยาศาสตร์คนต่อ ๆ มาจึงได้พยายามเสนอแบบจำลองอะตอมชนิดใหม่

เมื่อนักวิทยาศาสตร์ได้ทำการทดลองค้นคว้าได้ข้อมูลเกี่ยวกับอะตอมมากขึ้น พบว่าแบบจำลองของ dalton ไม่สามารถอธิบายได้ เช่น

1. ทำไมอะตอมของธาตุต่างกันจึงมีมวลต่างกัน

2. อะตอมของธาตุชนิดเดียวกันอาจมีสมบัติต่างกันได้ (เช่น ไฮโดรเจนมี 3 ไอโซโทป1H,2H และ3H เป็นธาตุชนิดเดียวกัน แต่มีมวลต่างกัน)

3. ทำไมธาตุจึงมีความว่องไวในการเกิดปฏิกิริยาต่างกัน

4. ทำไมธาตุหนึ่งๆทำปฏิกิริยาได้เฉพาะบางธาตุ

5. อะตอมทำให้เกิดขึ้นใหม่หรือเปลี่ยนไปเป็นอะตอมของธาตุอื่นได้ หรือสามารถสังเคราะห์อะตอมของธาตุใหม่ได้โดยอาศัยปฏิกิริยานิวเคลียร์

ด้วยสาเหตุดังกล่าวจึงทำให้มีผู้ศึกษาค้นคว้าแบบจำลองอะตอมใหม่เพื่ออธิบายสิ่งที่เกิดขึ้น

บทเรียนที่ 3 แบบจำลองอะตอมของทอมสัน(1)

การทดลองของทอมสันเกี่ยวกับหลอดรังสีแคโทด

เซอร์โจเซฟ จอห์น ทอมสัน (Sir Loseph John Thomson) ได้ทำการทดลองเกี่ยวกับการนำไฟฟ้าของก๊าซในหลอดรังสีแคโทดและ นอกจากนี้ยังมีนักวิทยาศาสตร์อื่น ๆ ที่สนใจเกี่ยวกับเรื่องนี้ เช่น ยูจีน โกลด์สไตน์ (Eugene Goldstein) และวิลเฮล์ม วีน (Wilhelm Wein) ซึ่งได้ทำการทดลองเกี่ยวหลอดรังสีแคโทด

โดยทอมสัน ได้ ดัดแปลงลักษณะของหลอดรังสีแคโทดจากเดิมเล็กน้อย เช่นมีการเติมฉากเรืองแสงไว้ในหลอดรังสีด้วย ดังในรูป และทอมสันได้นำผลการทดลองในลักษณะต่าง ๆ มาสรุปเกี่ยวกับแบบจำลองอะตอม โดยทำเป็นขั้น ๆ ดังนี้

1.บรรจุก๊าซชนิดหนึ่งในหลอดรังสีแคโทดที่ภายในมีขั้วไฟฟ้าแอโนด และแคโทดต่ออยู่กับเครื่องกำเนิดไฟฟ้ากระแสตรง ศักย์สูงที่ขั้วแอโนดเจาะรูเล็ก ๆ ตรงกลาง และปลายด้านหนึ่งของหลอดรังสีมีฉากเรืองแสง ก. ทำด้วย ZnS วางไว้ นำหลอดรังสีนี้ต่อเข้ากับเครื่องสูบสูญญากาศ

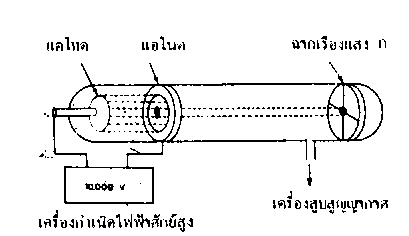
ในตอนแรกความดันในหลอดแก้วมีมาก จะยังไม่เห็นการเปลี่ยนแปลงใด ๆ ที่ฉากเรืองแสง แม้ว่าจะใช้ศักย์ไฟฟ้าสูง ๆเมื่อลดความดันในหลอดแก้วให้ต่ำลงมาก ๆ จนเกือบเป็นสุญญากาศ จะพบว่ามีจุดเรืองแสง หรือมีจุดสว่างบนฉากเรืองแสง ก.

เนื่องจาก ZnS มีสมบัติพิเศษคือ ถ้าอนุภาคมีประจุมากระทบจะทำให้เกิดการเรืองแสงขึ้น ดังนั้นจากผลการทดลองทำให้ ทอมสันตั้งสมมติฐานว่า

จะต้องมีรังสีชนิดหนึ่งซึ่งมีประจุไฟฟ้าพุ่งเป็นเส้นตรงจากขั้วแคโทดมายังฉากเรืองแสง ก. ซึ่งรังสีนี้อาจจะเกิดจากก๊าซที่มีอยู่ในหลอดแก้วนั้น หรืออาจจะเกิดจากโลหะที่ทำขั้วไฟฟ้าก็ได้ ซึ่งทอมสันยังไม่ทราบ

รวมทั้งยังไม่ทราบว่ารังสีที่พุ่งออกมานั้นมีประจุเป็นอย่างไร แต่ี้ทอมสันได้คาดว่าอะตอมคงจะไม่ใช่เป็นทรงกลมตันดังแบบจำลองของดอลตันแน่ แต่จะต้องมีอนุภาคเล็ก ๆ ที่มีประจุเป็นองค์ประกอบด้วย

การทดลองเพื่อทดสอบอนุภาคที่เกิดขึ้น

ในการทดสอบว่าประจุไฟฟ้าที่มากระทบฉากเรืองแสง ก. เป็นประจุบวกหรือลบ ทอมสันจึงได้ทดลองต่อไปโดยใช้สนามไฟฟ้าเข้าช่วย โดยยึดหลักที่ว่า อนุภาคที่มีประจุจะต้องเกิดการเบี่ยงเบนในสนามไฟฟ้าถ้าอนุภาคนั้นมีประจุบวกจะเบี่ยงเบนเข้าหาขั้วลบของสนามไฟฟ้าและถ้ามีประจุลบจะเบี่ยงเบนเข้าหาขั้วบวกทั้งนี้ศึกษาการเบี่ยงเบนได้จากฉากเรืองแสง

เมื่อเพิ่มขั้วไฟฟ้าเข้าไป 2 ขั้ว โดยให้ขั้วไฟฟ้าทั้งสอง มีสนามไฟฟ้าตั้งฉากกับทิศทางของรังสีดังในรูป

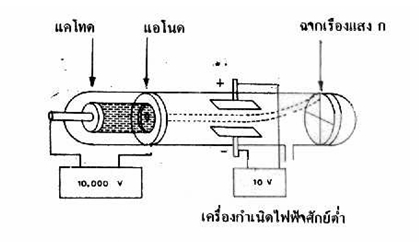
จากการทดลองพบว่า

- จุดสว่างบนฉากเรืองแสง ก. เบนไปจากตำแหน่งเดิม คือ เบี่ยงเบนขึ้นสู่ด้านบนซึ่งถ้าลากเส้นจากขั้วไฟฟ้าจะเห็นว่ารังสีนั้นเบี่ยงเบนเข้าหาขั้วบวกของสนามไฟฟ้า

แสดงว่ารังสีจะต้องประกอบด้วยอนุภาคที่มีประจุลบเนื่องจากรังสีนี้เคลื่อนที่ออกมาจากขั้วแคโทดซึ่งเป็นขั้วลบ จึงเรียกรังสีนี้ว่า รังสีแคโทดและเรียกหลอดแก้วที่ใช้ในการทดลองว่า หลอดรังสีแคโทด

ข้อสรุปที่ทอมสันได้

- ทอมสันได้ตั้งสมมติฐานขึ้นว่าอะตอมประกอบด้วยอนุภาคเล็กๆ ที่ส่วนหนึ่งมีประจุลบ

แต่มีประเด็นที่ต้องศึกษาเพิ่มอีก 2 ประเด็นคือ

ประเด็นที่ 1 อนุภาคที่มีประจุลบเหล่านี้ เกิดจากก๊าซในหลอดรังสี หรือเกิดจากขั้วไฟฟ้า

ประเด็นที่ 2 รังสีแคโทดนี้จะเหมือนกันหรือไม่จะประกอบด้วยอนุภาคชนิดเดียวกันหรือไม่ถ้าใช้ก๊าซต่างชนิดกันจะมีลักษณะเหมือนหรือต่างกันอย่างไร

ผลการศึกษาเพิ่มเติมของทอมสัน

ทอมสันศึกษาสมบัติของรังสีแคโทดโดยหาอัตราส่วนระหว่างประจุต่อมวลของรังสีนั้นทั้งนี้อาศัยหลักที่ว่านอกจากรังสีแคโทดจะเบี่ยงเบนได้ในสนามไฟฟ้าแล้ว ยังสามารถเบี่ยงเบนได้ในสนามแม่เหล็กด้วย

ในตอนแรกทอมสันได้ทดลอง

- เปลี่ยนก๊าซชนิดต่าง ๆ ในหลอดรังสีแคโทดแล้วทดลองในทำนองเดียวกัน ปรากฏผลการทดลองได้ผลเหมือนเดิม

-เปลี่ยนชนิดของขั้วไฟฟ้าที่ใช้ทำแคโทดก็ยังคงพบว่าได้ผลการทดลองเหมือนเดิม
(คือจะมีรังสีที่ประกอบด้วยอนุภาคที่มีประจุลบพุ่งมาที่ฉากเรืองแสง ก. และรังสีเกิดการเบี่ยงเบนเข้าหาขั้วบวกของสนามไฟฟ้า จึงทำให้ไม่สามารถจะพิสูจน์ว่าอนุภาคที่มีประจุลบนั้นเป็นอนุภาคชนิดเดียวกันหรือไม่)

ดังนั้นทอมสันจึงได้ทำการทดลองต่อโดยนำหลอดรังสีวางไว้ในสนามแม่เหล็ก ทั้งนี้ในทิศทางของสนามแม่เหล็กตั้งฉากกับสนามไฟฟ้าดังรูป ในช่วงแรกที่ใส่สนามแม่เหล็กเข้าไป จุดสว่างบนฉากเรืองแสง ก. จะเบี่ยงเบนขึ้นด้านบน เมื่อใส่สนามแม่เหล็กเข้าไป และเพิ่มอำนาจสนามแม่เหล็กทีละน้อยจะพบว่าจุดสว่างบนฉากเรืองแสง ก. ค่อย ๆ มีการเบี่ยงเบนน้อยลง คือ จุดเรืองแสงค่อย ๆ กลับมาสู่ตำแหน่งเดิมของตอนที่ไม่มีสนามไฟฟ้า แสดงว่าในขณะนี้ความแรงของสนามไฟฟ้ามีค่าเท่ากับความแรงของสนามแม่เหล็ก จุดสว่างบนฉากเรืองแสงจึงไม่มีการเบี่ยงเบน

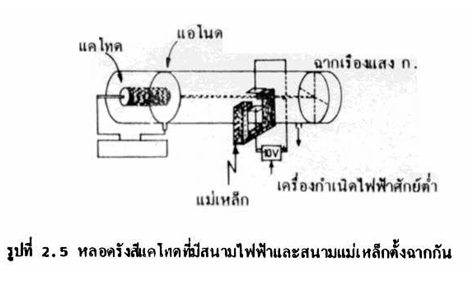
เมื่อนำความแรงเนื่องจากสนามไฟฟ้า และความแรงเนื่องจากสนามแม่เหล็กที่กระทำต่ออนุภาคลบมาคำนวณอัตราส่วนของประจุต่อมวล (e/m) ของอนุภาคลบนั้น ปรากฏว่าได้ค่าคงที่เท่ากันทุกครั้ง ไม่ว่าทอมสันจะใช้ก๊าซชนิดใด หรือไม่ว่าจะใช้โลหะใดเป็นแคโทดคือได้

e/m= 1.7 X 108 คูลอมบ์/กรัม

จากผลการทดลองและผลการคำนวณ ทำให้ทอมสันสรุปว่า

“อนุภาคลบในรังสีแคโทดจะต้องมีลักษณะเหมือนกัน และอะตอมทุกชนิดย่อมจะมีอนุภาคที่มีประจุลบเป็นองค์ประกอบเหมือนกัน และเรียกอนุภาคลบนี้ว่าอิเล็กตรอน”

เมื่อทดลองถึงตอนนี้ทำให้ทอมสันสรุปได้ว่า อะตอมไม่ใช่สิ่งที่เล็กที่สุด อะตอมของธาตุทุกชนิดจะต้องประกอบด้วยอิเล็กตรอนและอนุภาคอื่น ๆ ซึ่งในขณะนั้นยังไม่ทราบ

บทเรียนที่ 4 แบบจำลองอะตอมของทอมสัน(2)

หลอดรังสีแคโทด

เป็นเครื่องที่ใช่ทดลองเกี่ยวกับการนำไฟฟ้าโดยหลอดรังสีแคโทดจะมีความดันต่ำมาก และความต่างศักย์สูงมาก วิลเลียม ครูกส์ได้สร้างหลอดรังสีแคโทดขึ้นมาโดยใช้แผ่นโลหะ 2 แผ่นเป็นขั้วไฟฟ้า โดยต่อขั้วไฟฟ้าลบกับขั้วลบของเครื่องกำเนิดไฟฟ้าเรียกว่า แคโทด และต่อขั้วไฟฟ้าบวกเข้ากับขั้วบวกของเครื่องกำเนิดไฟฟ้าเรียกว่า แอโนด

การค้นพบอิเล็กตรอนเซอร์โจเซฟ จอห์น ทอมสัน ดัดแปลงหลอดรังสีใหม่ ดังรูป

รังสีพุ่งจากด้าแคโทดไปยังด้านแอโนด และจะมีรังสีส่วนหนึ่งทะุลุออกไปกระทบกับฉากเรืองแสงหลังจากนั้นทอมสันได้เพิ่มขั้วไฟฟ้าเข้าไปในหลอดรังสีแคโทดดังรูป

ปรากฎว่า รังสีนี้จะเบี่ยงเบนเข้าหาขั้วบวก แสดงว่า รังสีนี้ต้องเป็นประจุลบแต่ไม่ทราบว่าเกิดจากก๊าซในหลอดรังสีแคโทดหรือเกิดจากขั้วไฟฟ้าทอมสันจึงทำการทดลองเกี่ยวกับการนำไฟฟ้าของก๊าซในหลอดรังสีแคโทดพบว่าไม่ว่าจะใช้ก๊าซใดบรรจุในหลอดหรือใช้โลหะใดเป็นแคโทดจะได้ผลการทดลองเหมือนเดิมจึงสรุปได้ว่า อะตอมทุกชนิดมีอนุภาคที่มีประจุลบเป็นองค์ประกอบ เรียกว่า "อิเล็กตรอน"

การค้นพบโปรตอนเนื่องจากอะตอมเป็นกลางทางไฟฟ้า และการที่พบว่าอะตอมของธาตุทุกชนิดประกอบด้วยอิเล็กตรอนซึ่งมีประจุไฟฟ้าเป็นลบ ทำให้นักวิทยาศาสตร์เชื่อว่าองค์ประกอบอีกส่วนหนึ่งของอะตอม จะต้องมีประจุบวกด้วย ออยแกน โกลด์สไตน์ (Eugen Goldstein) นักวิทยาศาสตร์ชาวเยอรมัน ได้ทดลองเกี่ยวกับหลอดรังสีแคโทด โดยดัดแปลงหลอดรังสีแคโทด ดังรูป

ผลการทดลองของโกสไตน์

เมื่อผ่านกระแสไฟฟ้า ปรากฏว่ามีจุดสว่างเกิดขึ้นทั้งฉากเรืองแสง ก. และฉากเรืองแสง ข.

โกลสไตน์ได้อธิบายว่าจุดเรืองแสงที่เกิดขึ้นบนฉากเรืองแสงก.จะต้องเกิดจากที่ประกอบด้วยอนุภาคที่มีประจุไฟฟ้าบวกเคลื่อนที่ผ่านรูตรงกลางของแคโทด ไปยังฉากเรืองแสงแต่ยังไม่ทราบว่ารังสีที่มีประจุไฟฟ้าบวกนี้เกิดจากอะตอมของก๊าซหรือเกิดจากอะตอมของขั้วไฟฟ้า และมีลักษณะเหมือนกันหรือไม่

โกลสไตน์ได้ทดลองเปลี่ยนชนิดของก๊าซในหลอดแก้วปรากฏว่าอนุภาคที่มีประจุไฟฟ้าบวกเหล่านี้มีอัตราส่วนประจุต่อมวลไม่เท่ากัน ขึ้นอยู่กับชนิดของก๊าซที่ใช้และเมื่อทดลองเปลี่ยนโลหะที่ใช้ทำเป็นขั้วไฟฟ้าหลายๆชนิดแต่ให้ก๊าซในหลอดแก้วชนิดเดียวกัน ปรากฏว่า ผลการทดลองได้อัตราส่วนประจุต่อมวลเท่ากันแสดงว่าอนุภาคบวกในหลอดรังสีแคโทดเกิดจากก๊าซ
ไม่ได้เกิดจากขั้วไฟฟ้า

สรุปแบบจำลองของทอมสัน
จากผลการทดลอง ทั้งของทอมสันและโกลด์สไตน์ ทำให้ทอมสันได้ข้อมูลเกี่ยวกับอะตอมมากขึ้น จึงได้เสนอแบบจำลองอะตอม ดังนี้อะตอมมีลักษณะเป็นทรงกลมประกอบด้วยอนุภาคโปรตอนที่มีประจุไฟฟ้าเป็นบวกและอนุภาคอิเล็กตรอนที่มีประจุไฟฟ้าเป็นลบ กระจัดกระจายอย่างสม่ำเสมอในอะตอมอะตอมที่มีสภาพเป็นกลางทางไฟฟ้าจะมีจำนวนประจุบวกเท่ากับจำนวนประจุลบ

บทเรียนที่ 5 การค้นพบโปรตอน

การค้นพบโปรตอน

เนื่องจากอะตอมเป็นกลางทางไฟฟ้า และการที่พบว่าอะตอมของธาตุทุกชนิดจะต้องประกอบด้วยอิเล็กตรอนซึ่งมีประจุลบ ทำให้นักวิทยาศาสตร์เชื่อว่า องค์ประกอบอีกส่วนหนึ่งของอะตอมจะต้องมีอนุภาคที่มีประจุบวกอยู่ด้วย

ออยเกน โกลด์สไตน์ (Eugen Goldstein) นักวิทยาศาสตร์ชาวเยอรมัน ได้ทำการทดลองเกี่ยวกับหลอดรังสีแคโทด โดยดัดแปลงหลอดรังสีแคโทดเล็กน้อย ดังในรูป

โกลด์สไตน์ได้เลื่อนขั้วแคโทดและแอโนดมาไว้เกือบตรงกลาง แล้วเพิ่มฉากเรืองแสง ข. ที่ปลายอีกด้านหนึ่งของหลอดแก้ว โดยคิดว่าการที่อนุภาคที่มีประจุลบสามารถเคลื่อนที่ผ่านขั้วแอโนดไปที่ฉากเรืองแสง ก. ได้ อนุภาคที่มีประจุบวกก็ควรจะเคลื่อนที่ผ่านแคโทดไปที่ฉากเรืองแสง ข. ได้เช่นเดียวกัน ดังนั้นจึงเจาะรูตรงกลางของขั้วแอโนดและแคโทดไว้ จากการทดลองเมื่อผ่านกระแสไฟฟ้า ปรากฏว่ามีจุดสว่างเกิดขึ้นทั้งบนฉากเรืองแสง ก. และ ข. ซึ่งโกลด์สไตน์อธิบายว่าจุดสว่างที่เกิดบนฉากเรืองแสง ข. จะต้องเกิดจากรังสีที่ประกอบด้วยอนุภาคที่มีประจุไฟฟ้าบวกเคลื่อนที่ผ่านรูตรงกลางของแคโทดไปยังฉากเรืองแสง แต่ยังไม่ทราบว่ารังสีที่มีประจุไฟฟ้าบวกนี้เกิดจากอะตอมของก๊าซหรือเกิดจากอะตอมของขั้วไฟฟ้า และมีลักษณะเหมือนกันหรือไม่

จากการทดลองหลายครั้ง ๆ โดยการเปลี่ยนชนิดของก๊าซในหลอดแก้ว ปรากฏว่าอนุภาคที่มีประจุบวกเหล่านี้มีอัตราส่วนของประจุต่อมวลไม่เท่ากัน ขึ้นอยู่กับชนิดของก๊าซที่ใช้ และเมื่อทดลองโดยเปลี่ยนโลหะที่ใช้ทำขั้วไฟฟ้าหลาย ๆ ชนิด แต่ใช้ก๊าซในหลอด แก้วชนิดเดียวกัน ปรากฏว่าผลการทดลองได้อัตราส่วนของประจุต่อมวลเท่ากัน แสดงว่าอนุภาคบวกในหลอดรังสีแคโทดเกิดจากก๊าซ ไม่ได้เกิดจากขั้วไฟฟ้า

ต่อมาโกลด์สไตน์ได้พบว่าถ้าทำการทดลองโดยใช้ก๊าซไฮโดรเจน จะได้อนุภาคบวกที่มีจำนวนประจุเท่ากับประจุของอิเล็กตรอน และเรียกอนุภาคบวกที่เกิดจากก๊าซไฮโดรเจนว่า “โปรตอน” อะตอมของก๊าซไฮโดรเจนจะมี 1 โปรตอน และอะตอมของธาตุอื่น ๆ อนุภาคบวกจะมีมากกว่า 1 โปรตอน แต่จำนวนโปรตอนและอิเล็กตรอนเท่ากัน

จากผลการทดลองที่ผ่านมา ทั้งของทอมสัน และโกลด์สไตน์ ทำให้ทอมสันได้ข้อมูลเกี่ยวกับอะตอมมากขึ้น จึงได้เสนอแบบจำลองอะตอมดังนี้

“อะตอมมีลักษณะเป็นทรงกลม ประกอบด้วยอนุภาคโปรตอนที่มีประจุบวกและอนุภาคอิเล็กตรอนซึ่งมีประจุลบกระจายอยู่ทั่วไปอย่างสม่ำเสมอในอะตอม อะตอมในสภาพที่เป็นกลางทางไฟฟ้าจะมีจำนวนประจุบวกเท่ากับประจุลบ”

รูปที่ 1-8 แบบจำลองอะตอม ของ thomsom

ทอมสันได้นำแบบจำลองดังกล่าวมาอธิบายผลการทดลองดังนี้ เมื่ออะตอมของโลหะที่เป็นขั้วไฟฟ้าแคโทดได้รับพลังงานจากเครื่องกำเนิดไฟฟ้า จนกระทั่งพลังงานนั้นมีค่ามากพอที่จะทำให้เกิดการแตกตัว (Ionization) ให้อิเล็กตรอนออกมา

พลังงาน + M (s) --------------> M (g) ® M+(g) + e-

M คือ อะตอมของโลหะที่เป็นขั้วแคโทด

อิเล็กตรอนที่ออกมาจากแคโทดจะเคลื่อนที่ไปยังแอโนด ซึ่งในขณะที่เคลื่อนที่จะมีการชนอะตอมของก๊าซที่อยู่ภายในหลอดด้วย เนื่องจากอิเล็กตรอนที่ออกมาจากแคโทดมีพลังงานติดตัวออกมาด้วย เมื่อมีการชนกับอะตอมของก๊าซจะมีการถ่ายเทพลังงาน ซึ่งถ้ามีการชนที่แรงพอจนทำให้อะตอมของก๊าซที่ถูกชนเกิดการแตกตัวให้อิเล็กตรอนและอนุภาคที่มีประจุบวกออกมาเช่นเดียวกัน

อิเล็กตรอนจากขั้วไฟฟ้า A (g)-----------------------> A+(g) + e-

อิเล็กตรอนทั้งหมดจากขั้วไฟฟ้าและจากก๊าซซึ่งเรียกรวมกันว่ารังสีแคโทดจะพุ่งไปยังขั้วแอโนด บางส่วนจะวิ่งผ่านรูที่เจาะไว้ตรงกลางขั้วแอโนดไปกระทบฉากเรืองแสงทำให้เกิดจุดสว่างบนฉากเรืองแสงขึ้น เนื่องจากอะตอมของธาตุทุกชนิดประกอบด้วยอิเล็กตรอนอย่างเดียวกัน ดังนั้นไม่ว่าจะใช้โลหะใดเป็นขั้วไฟฟ้า หรือใช้ก๊าซใดใส่ในหลอดแก้ว จะได้รังสีแคโทดนิดเดียวกัน อัตราส่วนระหว่างประจุต่อมวลจึงเท่ากัน

ในขณะที่อิเล็กตรอนวิ่งไปยังแอโนด อนุภาคที่มีประจุบวก คือ A+จะวิ่งไปยังแคโทด และบางส่วนจะผ่านแคโทดตรงรูที่เจาะไว้ตรงกลางกระทบกับฉากเรืองแสง ทำให้เกิดจุดสว่างบนฉากเรืองแสงขึ้น แต่เนื่องจากอะตอมของก๊าซแต่ละชนิดมีมวลไม่เท่ากัน ดังนั้นอัตราส่วนของประจุต่อมวลของอนุภาคบวกจึงไม่เท่ากัน (สำหรับก๊าซต่างชนิดกัน)

เช่น He (g)-------------> He+(g) + e-

H (g) ---------> H+(g) + e-

ประจุต่อมวลของ He+(g) กับ H+(g) ย่อมไม่เท่ากัน เพราะมวลอะตอมของ He และ H ไม่เท่ากัน

การหาค่าประจุของอิเล็กตรอน

ใน พ.ศ. 2451 โรเบิร์ต แอนดรูส์ มิลลิแกน (Robert Andrews Millikan) นักวิทยาศาสตร์ชาวอเมริกาได้ทำการทดลองหาค่าประจุของอิเล็กตรอน โดยใช้การทดลองที่เรียกว่า “Oil drop experiment”

เครื่องมือประกอบด้วยขั้วไฟฟ้า 2 ขั้ว ต่ออยู่กับเครื่องกำเนิดไฟฟ้า ขั้วไฟฟ้าบนเป็นขั้วบวก และขั้วไฟฟ้าด้านล่างเป็นขั้วลบ ขั้วไฟฟ้าทั้ง 2 ใส่ไว้ในกล่องซึ่งมีอากาศอยู่ภายใน

เมื่อพ่นหยดน้ำมันเม็ดเล็ก ๆ เข้าไประหว่างขั้วไฟฟ้าทั้งสอง เนื่องจากน้ำมันแต่ละหยดมีมวล ดังนั้นจึงถูกแรงดึงดูดของโลกทำให้ตกลงมาสู่ด้านล่าง ในขณะที่เม็ดน้ำมันยังไม่มีประจุไฟฟ้า การที่จะบังคับให้เคลื่อนที่ขึ้นลงจึงยังทำไม่ได้ ดังนั้นในตอนแรกจึงต้องเติมประจุลงบนหยดน้ำมันก่อนโดยการฉายรังสีเอ็กซ์ ( X-Ray) เข้าไป รังสีเอ็กซ์จะไปชนกับอากาศภายในกล่อง ทำให้อะตอมของอากาศเกิดการแตกตัว

X-rays ® A (g)-----------> A+(g) + e-

รูป 1-9 การทดลอง หาค่าประจุของอิเล็กตรอนโดยวิธีเม็ดน้ำมัน

อนุภาคบวกและอิเล็กตรอนที่เกิดขึ้นจะไปเกาะที่หยดน้ำมัน ทำให้หยดน้ำมันเกิดประจุ อิเล็กตรอนที่ไปเกาะที่หยดน้ำมันอาจจะไปเกาะเพียง 1 ตัว หรือหลายๆ ตัวก็ได้ เช่นเดียวกับอนุภาคบวกก็จะไปเกาะที่หยดน้ำมัน ซึ่งอาจจะมีอนุภาคบวกหลายตัวที่หยดน้ำมัน 1 หยด เมื่อหยดน้ำมันมีประจุในขณะที่กำลังเคลื่อนที่ลงมาด้วยแรงดึงดูดของโลก ถ้าใส่สนามไฟฟ้าเข้าไปในระหว่างขั้วไฟฟ้าทั้งสอง ขั้วไฟฟ้าบวกข้างบนจะดึงดูดกับหยดน้ำมันที่มีอิเล็กตรอนเกาะอยู่ ส่วนขั้วไฟฟ้าลบข้างล่างจะดึงดูดกับอนุภาคบวกทำให้หยดน้ำมันที่มีอนุภาคบวกเคลื่อนที่ลงได้เร็วขึ้น ซึ่งในที่นี้จะไม่ขอกล่าวถึงอนุภาคบวก แต่จะกล่าวถึงรายละเอียดเกี่ยวกับอิเล็กตรอนเท่านั้น

ในขณะที่ใส่สนามแม่เหล็กเข้าไป หยดน้ำมันที่มีอิเล็กตรอนเกาะอยู่จะมีประจุเป็นลบ และถูกดึงดูดให้ลอยขึ้นไปหาขั้วบวก ดังนั้นในตอนแรกหยดน้ำมันเหล่านี้จะเคลื่อนที่ลงได้ช้า และเมื่อเพิ่มศักย์ไฟฟ้าระหว่างขั้วให้มากขึ้น จนกระทั่งแรงดึงดูดเนื่องจากขั้วไฟฟ้ากับอิเล็กตรอนบนหยดน้ำมันเท่ากับแรงเนื่องจากแรงดึงดูดของโลก หยดน้ำมันเหล่านั้นจะลอยนิ่ง ซึ่งสามารถนำมาคำนวณค่าของประจุไฟฟ้าของอิเล็กตรอนแต่ละตัวได้

ถ้า m = มวลของหยดน้ำมัน

g = ค่าคงที่ของแรงดึงดูดของโลก

F1= แรงเนื่องจากแรงดึงดูดของโลกต่อหยดน้ำมัน

F1= mg

ถ้า E = สนามไฟฟ้า

q = ประจุไฟฟ้าบนหยดน้ำมัน

F2= แรงเนื่องจากสนามไฟฟ้าต่อหยดน้ำมัน

F2= Eq

เมื่อพิจารณาหยดน้ำมันที่ลอยนิ่ง หยดใดหยดหนึ่ง จะได้ว่า

แรงเนื่องจากแรงดึงดูดของโลก = แรงเนื่องจากสนามไฟฟ้า

mg = Eq

หรือ q =

ค่า E และ g สามารถหาได้จากเครื่องมือที่ใช้ ส่วน m ซึ่งเป็นมวลของหยดน้ำมันหาได้จากสูตร m = rd

เมื่อ r = รัศมีของหยดน้ำมัน

d = ความหนาแน่นของน้ำมัน

จะเห็นได้ว่า ค่า m , g และ E สามารถหาได้ ดังนั้นจึงคำนวณประจุที่อยู่บนหยดน้ำมันได้ จากการทดลองพบว่าประจุที่อยู่บนหยดน้ำมันนั้นมีค่าเท่ากับ 1.60x 10-19คูลอมบ์ หรือเป็นจำนวนเท่าของ 1.60x10-19คูลอมบ์ เช่น 2x1.60x 10-19, 3 x1.60x10-19คูลอมบ์ เป็นต้น แสดงว่าจำนวนประจุที่อยู่บนหยดน้ำมันที่มีค่าน้อยที่สุดคือ 1.60x10-19คูลอมบ์ จำนวนประจุอื่น ๆ จะเป็นจำนวนเท่าของ 1.60x10-19ดังนั้นค่าของประจุ 1.60x10-19คูลอมบ์ จึงเป็นค่าประจุของอิเล็กตรอน 1 ตัว กล่าวคือ

ถ้ามีอิเล็กตรอน 1 ตัว เกาะบนหยดน้ำมัน จะได้ประจุ = 1.60x10-19คูลอมบ์

ถ้ามีอิเล็กตรอน 2 ตัว เกาะบนหยดน้ำมัน จะได้ประจุ = 2x1.60x10-19คูลอมบ์

ถ้ามีอิเล็กตรอน 3 ตัว เกาะบนหยดน้ำมัน จะได้ประจุ = 3x1.60x10-19คูลอมบ์

ดังนั้น จากการทดลองของมิลลิแกนได้ประจุของอิเล็กตรอนมีค่าเท่ากับ1.60x10-19คูลอมบ์

การคำนวณหามวลของอิเล็กตรอน

จากการทดลองของทอมสันได้ค้าประจุต่อมวลของอิเล็กตรอน คือ

= 1.7 X 108คูลอมบ์/กรัม

จากการทดลองของมิลลิแกน

ได้ค่าประจุของอิเล็กตรอน (e) = 1.60 x 10-19คูลอมบ์

เพราะฉะนั้นหามวลของอิเล็กตรอนได้ m = 9.41 x 10-28กรัม

แบบจำลองอะตอมของทอมสันนับว่าเป็นก้าวสำคัญเกี่ยวกับการศึกษาโครงสร้างของอะตอม ทำให้ได้มโนภาพของอะตอมที่ถูกต้องยิ่งขึ้น แต่อย่างไรก็ตามแบบจำลองอะตอมของทอมสันก็ยังไม่สามารถจะอธิบายผลการทดลองใหม่ ๆ อีกเป็นจำนวนมาก ซึ่งแสดงว่ายังไม่ใช่แบบจำลองที่สมบูรณ์ เป็นผลให้มีการค้นคว้าเพิ่มเติมขึ้น และมีการเสนอแบบจำลองใหม่ ๆ ขึ้นมา

บทเรียนที่ 6 แบบจำลองอะตอมของรัทเทอร์ฟอร์ด

แบบจำลองอะตอมของรัทเทอร์ฟอรด์

หลังจากนักวิทยาศาสตร์ชาวฝรั่งเศส Henri Becquerel ได้พบสารกัมมันตรังสี และเรินต์เกน (W.K. Rontgen) ค้นพบ X-ray

Lord Ernest Ruthetford นักวิทยาศาสตร์ชาวนิวซีแลนด์ได้ทำการการศึกษาธรรมชาติของรังสีที่เกิดจากสารกัมมันตรังสี พบว่ามี 3 ชนิด คือ

1. รังสี เอลฟา ( α-ray) ประกอบด้วยอนุภาคที่มีประจุไฟฟ้าเป็นบวก (+2) เป็นนิวเคลียสของอะตอมของธาตุฮีเลียม คือประกอบด้วย Proton 2 ตัว และ Neutron 2 ตัว ( ) อำนาจผ่านทะลุวัตถุได้น้อยมาก ถูกกั้นโดยกระดาษเพียงแผ่นเดียวหรือสองแผ่น He42

2. รังสีเบตา (β-ray) ประกอบด้วยอิเล็กตรอนที่มีพลังงานสูง มีอำนาจการผ่านทะลุสูงกว่ารังสีเเอลฟา ถูกกั้นโดยใช้แผ่นโลหะบางๆ

3. รังสีแกมมา (γ-ray) แสดงสมบัติเป็นคลื่นแม่เหล็กไฟฟ้าที่มีความยาวคลื่นสั้นมากคล้าย X-ray รังสีแกมมาไม่มีมวลไม่มีประจุ มีอำนาจผ่านทะลุสูง ถูกกั้นได้โดยแผ่นตะกั่วหนา

หลังจากที่ได้ศึกษาเกี่ยวกับสารกัมมันตรังสีมากขึ้น ได้มีการค้นพบรังสีต่าง ๆ ซึ่งเกิดจากการสลายตัวของสารกัมมันตรังสี เช่น รังสีแอลฟา (a ) เบตา (b) และแกรมมา (g) โดยเฉพาะรังสีแอลฟาซึ่งจัดว่าเป็นอนุภาคที่มีประจุไฟฟ้าบวก และมีมวลมากกว่ารังสีเบตา และแกรมมา เมื่ออนุภาคแอลฟาเคลื่อนที่ไปกระทบกับอนุภาคอื่น ๆ ที่มีมวลน้อยกว่า จึงไม่ค่อยมีการเบี่ยงเบนซึ่งทำให้นักวิทยาศาสตร์บางท่านนำเอารังสีแอลฟาไปศึกษาเกี่ยวกับโครงสร้างของอะตอม เช่น เออร์เนสต์ รัทเทอร์ฟอร์ด (Ernest Rutherford) นักวิทยาศาสตร์ชาวนิวซีแลนด์ เป็นต้น

ในปี พ.ศ. 2454 รัทเทอร์ฟอร์ด ได้ทำการทดลองในประเภทอังกฤษร่วมกับ ฮันส์ ไกเกอร์ และเออร์เนส์ มาร์สเดน ศึกษาทิศทางการเคลื่อนที่ของอนุภาคแอลฟา เมื่อยิงอนุภาคแอลฟาซึ่งได้จากการสลายตัวของสารกัมมันตรังสี เข้าไปที่แผ่นทองคำบาง ๆ

การตรวจสอบทิศทางการเคลื่อนที่ของอนุภาคแอลฟาหลังจากกระทบแผ่นทองคำแล้ว ทำได้โดยใช้ฉากเรืองแสงขดเป็นวงกลมล้อมรอบแผ่นทองคำไว้ โดยเว้นที่เฉพาะบริเวณที่จะให้อนุภาคแอลฟาผ่านเข้ามาเท่านั้น ทุก ๆ ครั้งที่อนุภาคแอลฟากระทบฉากเรืองแสงจะพบว่ามีจุดสว่างเกิดขึ้นที่ฉากเรืองแสงนั้น (อนุภาคแอลฟาคือ นิวเคลียสของธาตุฮีเลียม ซึ่งประจุบวก ดังนั้นเมื่อกระทบฉากเรืองแสงจึงมีจุดสว่างเกิดขึ้น ทำให้ทราบทิศทางการเคลื่อนที่ของอนุภาคแอลฟา) จากการทดลองพบว่าอนุภาคแอลฟาส่วนใหญ่จะวิ่งเป็นแนวเส้นตรง ผ่านแผ่นทองคำไปกระทบฉากเรืองแสง ซึ่งก็คือบริเวณจุด ก. ที่อยู่หลังแผ่นทองคำในรูป บางส่วนจะเบี่ยงเบนไปจากแนวเส้นตรง คือบริเวณจุด ข. ของฉากเรืองแสง และมีน้อยครั้งมากที่อนุภาคสะท้อนกลับมากระทบฉากเรืองแสงที่จุด ค. ซึ่งอยู่หน้าแผ่นทองคำ

จากผลการทดลอง ทำให้รัทเทอร์ฟอร์ดแปลกใจมาก เพราะถ้านำแบบจำลองอะตอมของทอมสันมาอธิบายทิศทางที่น่าจะเกิดขึ้น เมื่อยิงอนุภาคแอลฟาไปที่แผ่นทองคำ อนุภาคส่วนใหญ่ควรจะเบี่ยงเบนไปจากแนวเส้นตรง ทั้งนี้ เพราะตามแบบจำลองอะตอมของทอมสัน อะตอมประกอบด้วยอนุภาคบวกและลบ กระจายอยู่ทั่วไปในอะตอม เมื่อยิงอนุภาคแอลฟาซึ่งมีประจุบวกเข้าไปในอะตอมของแผ่นทองคำ อนุภาคแอลฟาควรจะผลักกับโปรตอนซึ่งมีประจุบวกเหมือนกัน อันจะเป็นผลทำให้ทิศทางของอนุภาคแอลฟาเบี่ยงเบนไปดังในรูปที่ 1-12 แต่จากผลการทดลอง การที่อนุภาคแอลฟาส่วนใหญ่วิ่งผ่านแผ่นทองคำเป็นแนวเส้นตรง จึงทำให้รัทเทอร์ฟอร์ดแปลกใจมาก โดยเฉพาะอนุภาคแอลฟาส่วนที่สะท้อนกลับยิ่งทำให้แปลกใจมากยิ่งขึ้น ทั้งนี้เพราะการที่อนุภาคแอลฟาสะท้อนกลับได้แสดงว่าภายในอะตอมจะต้องมีสิ่งที่มีมวลมากขวางทางอยู่ เมื่ออนุภาคแอลฟาไปชนจึงเกิดการสะท้อนกลับ แต่จากแบบจำลองอะตอมของทอมสันภายในอะตอมไม่มีสิ่งหนึ่งสิ่งใดอยู่รวมกันเป็นกลุ่มเป็นก้อนเลย ดังนั้นการสะท้อนกลับของอนุภาคแอลฟาเป็นมุมมากกว่า 90 องศา จึงไม่มีทางเกิดขึ้นได้

แต่จากผลการทดลองของ Rutherford ปรากฎว่าอนุภาคแอลฟาส่วนใหญ่วิ่งผ่านแผ่นทองคำเป็นเส้นตรง และมีส่วนที่เบี่ยงเบนออก และบางส่วนสะท้อนกลับ แสดงว่าแบบจำลองของ Thomson ไม่สอดคล้องกับผลการทดลอง Rutherford อธิบายผลการทดลองดังนี้

1. การที่อนุภาคแอลฟาส่วนใหญ่วิ่งผ่านแผ่นทองคำเป็นเส้นตรงแสดงว่าอะตอมไม่ใช่ของแข็งทึบตันแต่ภายในอะตอมมีที่ว่างอยู่มาก (ผลการทดลอง จุด ก เป็นจุดที่รังสีแอลฟาผ่านช่องว่างในอะตอมไปยังฉากมาก จุดนี้เรืองแสงมาก แสดงว่าอะตอมมีช่องว่างมาก)

2. อนุภาคแอลฟาบางอนุภาคที่หักเหออกจากทางเดิมเพราะภายในอะตอมมีอนุภาคที่มีมวลมากและมีประจุเป็นบวกสูง มีขนาดเล็ก ดังนั้นเมื่ออนุภาคแอลฟาเข้าใกล้อนุภาคนี้จะถูกผลักให้เบนออกจากทางเดิม หรือเมื่อนุภาคแอลฟากระทบโดยตรงก็เกิดการสะท้อนกลับ (เกิดการเรืองแสงที่จุด ข และ ค

การที่อนุภาคแอลฟาส่วนใหญ่เคลื่อนที่ผ่านอะตอมของทองคำเป็นแนวเส้นตรง แสดงว่าภายในอะตอมทองคำควรจะมีที่ว่างเป็นจำนวนมาก และการที่อนุภาคแอลฟาบางส่วนสะท้อนกลับแสดงว่าภายในอะตอมควรจะมีอนุภาคอะไรสักอย่างที่รวมกันเป็นกลุ่มก้อน และมีปริมาณมากพอ รวมทั้งมีมวลมากพอที่จะทำให้อนุภาคสะท้อนกลับเมื่อกระทบถูกได้ เนื่องจากภายในอะตอม (ในขณะนั้น) มีแต่อิเล็กตรอนและโปรตอน โดยที่อิเล็กตรอนมีมวลน้อยมาก รัทเทอร์ฟอร์ดจึงคิดว่าอนุภาคส่วนที่มารวมกันเป็นกลุ่มก้อนจึงน่าจะเป็นอนุภาคของโปรตอน ดังนั้นเพื่อที่จะอธิบายผลการทดลอง รัทเทอร์ฟอร์ดจึงเสนอแบบจำลองแบบใหม่ เรียกว่าแบบจำลองอะตอมของรัทเทอร์ฟอร์ดดังนี้

“อะตอมมีลักษณะเป็นทรงกลม ประกอบด้วยนิวเคลียสซึ่งก็คือโปรตอนที่รวมกันอยู่ตรงกลางของอะตอม และมีอิเล็กตรอนวิ่งวนอยู่รอบ ๆ นิวเคลียส นิวเคลียสมีขนาดเล็ก แต่มีมวลมากและมีประจุบวก ส่วนอิเล็กตรอนจะมีมวลน้อยและมีประจุลบ จำนวนอิเล็กตรอนจะเท่ากับจำนวนโปรตอน”

บทเรียนที่ 7 คลื่น สมบัติของคลื่นและสเปกตรัมของแสง (1)

แบบจำลองอะตอมของรัทเทอร์ฟอร์ด ใช้อธิบายเกี่ยวกับการทดลองยิงอนุภาคแอลฟาไปที่แผ่นทองคำ แต่อธิบายปัญหาบางอย่างไม่ได้ เช่น ทำไมโปรตอนซึ่งมีประจุบวกจึงรวมกันเป็นนิวเคลียสได้ และทำไมอิเล็กตรอนซึ่งมีประจุลบจึงเคลื่อนที่รอบ ๆ นิวเคลียสได้

หลังจากการค้นพบนิวตรอน สามารถอธิบายเหตุผลที่โปรตอนสามารถรวมกันเป็นนิวเคลียสได้ 2 ลักษณะดังนี้

1.โปรตอนและนิวตรอนที่จะเปลี่ยนกลับไปกลับมาได้

ถ้า n คือ นิวตรอน และ p คือ โปรตอน จะเขียนสมการแสดงการเปลี่ยนแปลงกลับไปกลับมาระหว่างโปรตอน และนิวตรอนได้ดังนี้

Neutron + Positive charge ® Proton

หรือ n + e ® p

และ Proton + Negative charge ® Neutron

หรือ p + e ® n

จะเห็นได้ว่า โปรตอนสามารถเปลี่ยนไปเป็นนิวตรอนได้โดยอาศัยอิเล็กตรอน และนิวตรอนสามารถเปลี่ยนเป็นโปรตอนได้โดยโปสิตรอน (e ) ซึ่งเป็นอนุภาคที่ไม่เสถียรภายในนิวเคลียส เขียนเป็นสมการรวมได้ดังนี้

การที่โปรตอนและนิวตรอนสามารถจะเปลี่ยนกลับไปกลับมาได้จึงก่อให้เกิดแรงยึดเหนี่ยวระหว่างอนุภาคทั้งสอง ซึ่งทำให้อนุภาคทั้งสองอยู่ด้วยกันได้ และทำให้นิงเคลียสมีความเสถียร

2.พิจารณาในแง่ของประจุเนื่องจากนิวตรอนไม่มีประจุไฟฟ้าจึงเป็นกลางทางไฟฟ้า นิวตรอนจึงไม่มีแรงดูดหรือแรงผลักระหว่างอนุภาค ดังนั้นจึงทำหน้าที่เชื่อม (Cement) ระหว่างโปรตอนกับโปรตอน โดยการแทรกอยู่ระหว่างโปรตอนกับโปรตอนซึ่งทำให้โปรตอนอยู่ในระหว่าง ลดแรงผลักลงได้ จึงทำให้โปรตอนอยู่รวมกันได้

จะเห็นได้ว่าแบบจำลองอะตอมใหม่ที่มีนิวตรอนสามารถอธิบายการรวมตัวกันของโปรตอนในนิวเคลียสได้ แต่ยังไม่สามารถอธิบายได้ว่าอิเล็กตรอนอยู่รวมกันรอบ ๆ นิวเคลียสได้อย่างไร อิเล็กตรอนทั้งหมดอยู่รวมกันหรือมีการแบ่งกลุ่ม ๆ หรือมีตัวกลางแบบเดียวกับนิวตรอนในนิวเคลียส นอกจากนี้ยังไม่สามารถอธิบายได้ว่าเหตุใดเมื่อเผาสารประกอบชนิดต่าง ๆ สีของเปลวไฟจึงไม่เหมือนกัน

นักวิทยาศาสตร์ได้พยายามศึกษาลักษณะของการจัดเรียงอิเล็กตรอนรอบ ๆ อะตอม โดยแบ่งการศึกษาออกเป็น 2 ส่วนส่วนแรกเป็นการศึกษาเกี่ยวกับสเปกตรัมของอะตอมซึ่งจะทำให้ทราบว่าภายในอะตอมมีการจัดระดับพลังงานเป็นชั้น ๆ ในแต่ละชั้นจะมีอิเล็กตรอนบรรจุอยู่ส่วนที่สองเป็นการศึกษาเกี่ยวกับพลังงานไอออนไนเซชัน เพื่อจะดูว่าในแต่ละระดับพลังงานจะมีอิเล็กตรอนบรรจุอยู่ได้กี่ตัว

สเปกตรัมหมายถึงอนุกรมของแถบสีหรือ หรือเส้นที่ได้จากการผ่านพลังงานรังสีเข้าไปในสเปกโตรสโคป ทำให้พลังงานรังสีแยกออกเป็นแถบหรือเป็นเส้นที่มีความยาวคลื่นต่าง ๆ เรียงลำดับกันไป

สเปกโตรสโคป (Spectroscope) หรือสเปกโตรมิเตอร์ (Spectrometer)หมายถึง เครื่องมือที่ใช้แยกสีตามความถี่ หรือเครื่องมือที่ใช้ศึกษาเกี่ยวกับสเปกตรัม

สเปกตรัม แบ่งเป็น 2 ประเภท คือ

ก. สเปกตรัมแบบต่อเนื่อง (Continuous spectrum) เป็นสเปกตรัมที่ประกอบด้วยแถบสีที่มีความถี่ต่อเนื่องกันไปอย่างกลมกลืนกัน เช่น สเปกตรัมของแสงอาทิตย์

ข. สเปกตรัมไม่ต่อเนื่อง (Discontinuous spectrum) หรือเรียกเส้นสเปกตรัม ลักษณะของสเปกตรัมจะเป็นเส้นหรือแถบสีเล็ก ๆ ที่ไม่เกิดต่อเนื่องกันไป แต่มีการเว้นช่วงของความถี่ที่เส้นสเปกตรัมเกิด เช่น สเปกตรัมธาตุไฮโดรเจน ธาตุฮีเลียม เป็นต้น

สเปกตรัมที่ไม่ต่อเนื่องจะมีบทบาทที่สำคัญในการศึกษาโครงสร้างอะตอม เนื่องจากอะตอมของธาตุต่าง ๆ จะมีเส้นสเปกตรัมเฉพาะตัวคล้ายกับลายนิ้วมือของคนแต่ละคนที่ไม่เหมือนกันสำหรับสเปกตรัมของธาตุ ถ้าพลังงานรังสีเกิดจากการเปลี่ยนแปลงของอะตอมจะเรียกว่า “อะตอมมิกสเปกตรัม (Atomic spectrm) ”

ความยาวคลื่น (Wavelength) ใช้สัญลักษณ์เป็น l (อ่านว่า แลมบ์ดา) เป็นสมบัติที่สำคัญของคลื่นหมายถึง ระยะทางที่คลื่นเคลื่อนที่ครบ 1 รอบพอดี (คือระยะทางจากจุด ก. ถึงจุด ข. ในรูป หรือระยะทางจากจุดประปลายหนึ่งไปยังอีกปลายหนึ่ง) ความยาวคลื่นมีหน่วยเป็นเมตร

( m ) หรือหน่วยย่อยของเมตร เช่น นาโนเมตร (nm) โดย 1 nm = 10-9เมตร

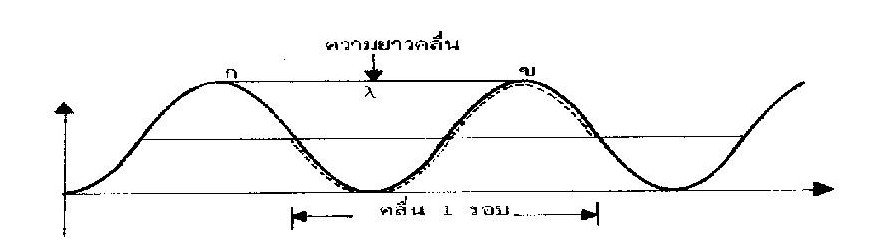
ความถี่ของคลื่น ใช้สัญลักษณ์เป็น n (อ่านว่า นิว) หมายถึง จำนวนรอบของคลื่นที่เคลื่อนที่ผ่านจุดใดจุดหนึ่งในเวลา 1 วินาที ความถี่ของคลื่นจึงมีหน่วยเป็นจำนวนรอบต่อวินาที ( S-1หรือ cycle/s) หน่วยนี้มีชื่อเรียกอีกอย่างหนึ่งว่าเฮิร์ตซ์ ( Hertz) หรือใช้สัญลักษณ์เป็น Hz

แอมปลิจูด ( Amplitude) คือ ความสูงของยอดคลื่น

คลื่นที่จะศึกษากันในที่นี้เป็นคลื่นแม่เหล็กไฟฟ้าในช่วงความยาวคลื่นระหว่าง 380-750 nm ซึ่งเป็นช่วงคลื่นที่มีความยาวและความถี่ที่ประสาทตาของคนจะรับได้เรียกคลื่นแม่เหล็กไฟฟ้าช่วงดังกล่าวนี้ว่า “แสงขาว (Visibel light)” สำหรับช่วงอื่น ๆ นอกจากนี้จะไม่นำมาศึกษาเนื่องจากประสาทตาไม่สามารถจะรับได้ เช่น ช่วงอัลตราไวโอเลต (Utraviolet หรือตัวอย่คือ U.V. ) อินฟาเรด (Infrared หรือตัวย่อ I.R.) และไมโครเวฟ (Microwave) เป็นต้น

ตารางที่3 สมบัติของคลื่นในช่วงความยาวต่าง ๆ กัน บางช่วง

การศึกษาเกี่ยวกับสเปกตรัมนี้มีมาตั้งแต่สมัยนิวตัน โดยใช้ปริซึมแยกแสงอาทิตย์ออกเป็นแถบสีรวม 7 สี ซึ่งภายหลังเคอร์ชอฟ (Gustav Krchhoff) ชาวเยอรมัน ได้ประดิษฐ์สเปกโตรสโคปขึ้น ใช้ในการแยกสเปกตรัมของแสงขาว และต่อมาบุนเซน (Robert Bunsen) ได้นำความรู้เกี่ยวกับสเปกตรัมไปวิเคราะห์แร่ชนิดต่าง ๆ ซึ่งทำให้ทราบว่าแร่นั้นมีธาตุอะไรเป็นองค์ประกอ

บทเรียนที่ 8 คลื่น สมบัติของคลื่นและสเปกตรัมของแสง (2)

การศึกษาเกี่ยวกับสเปกตรัมนี้มีมาตั้งแต่สมัยนิวตัน โดยใช้ปริซึมแยกแสงอาทิตย์ออกเป็นแถบสีรวม 7 สี ซึ่งภายหลังเคอร์ชอฟ (Gustav Krchhoff) ชาวเยอรมัน ได้ประดิษฐ์สเปกโตรสโคปขึ้น ใช้ในการแยกสเปกตรัมของแสงขาว และต่อมาบุนเซน (Robert Bunsen) ได้นำความรู้เกี่ยวกับสเปกตรัมไปวิเคราะห์แร่ชนิดต่าง ๆ ซึ่งทำให้ทราบว่าแร่นั้นมีธาตุอะไรเป็นองค์ประกอบ

เมื่อให้แสงขาวส่องผ่านปริซึม แสงขาวจะแยกออกเป็นแถบสีต่าง ๆ ต่อเนื่องกัน 7 สี เหมือนสีรุ้ง คือ สีม่วง คราม น้ำเงิน เขียว เหลือง ส้ม และแดง นักวิทยาศาสตร์เรียกแถบสีต่อเนื่องกันทั้ง 7 สีนี้ว่า “ สเปกตรัมของแสงสีขาว ” การที่แสงขาวสามารถแยกออกเป็นสเปกตรัมสีต่าง ๆ กันก็เนื่องจากแสงขาวประกอบด้วยสีต่าง ๆ ทั้ง 7 สี ซึ่งมีความยาวคลื่นต่าง ๆ จะทำให้เกิดการหักเหตามขนาดของมุมต่าง ๆ แสงที่มีความยาวคลื่นไม่เท่ากันจะเกิดการหักเหในปริซึมได้ไม่เท่ากัน ซึ่งทำให้เกิดการแยกออกเป็นแถบแสงสีต่าง ๆ และต่อเนื่องกันเป็นแถบสเปกตรัม

ตารางที่4 แถบสีของสเปกตรัมของแสงขาว

สำหรับคลื่นแม่เหล็กไฟฟ้าในช่วงอื่น ๆ ก็มีการหักเหเมื่อผ่านปริซึมหรือผ่านตัวกลางเช่นเดียวกัน แต่ไม่สามารถมองเห็นได้เหมือนแสงขาว การศึกษาสเปกตรัมของคลื่นแม่เหล็กไฟฟ้าได้รับความสนใจเป็นอย่างมากนักวิทยาศาสตร์ ซึ่งต่อมามักซ์ พลังค์(Max Planck)นักวิทยาศาสตร์ ชาวเยอรมัน ได้พบว่าคลื่นแม่เหล็กไฟฟ้าหรือแสงเป็นพลังงานรูปหนึ่งและพลังงานของคลื่นแม่เหล็กไฟฟ้ามีส่วนสัมพันธ์กับความถี่และความยาวของคลื่นโดยสรุปเป็นกฎว่า

“พลังงานของคลื่นแม่เหล็กไฟฟ้าจะเป็นสัดส่วนโดยตรงกับความถี่ของคลื่นนั้น”

เขียนเป็นความสัมพันธ์ได้ดังนี้

E a

E = h

เมื่อ E = พลังงานของคลื่นแม่เหล็กไฟฟ้า (หน่วยเป็น จูล )

h = ค่าคงที่ของพลังค์ ( Plank,constant) = 6.625 x 10-34Js

= ความถี่ของคลื่นแม่เหล็กไฟฟ้า (Hz หรือ s-1)

เรียกสมการดังกล่าวนี้ว่ากฎของพลังค์

ในการศึกษาเกี่ยวกับคลื่นโดยทั่ว ๆ ไปมักจะวัด เป็นความยาวคลื่น ซึ่งความยาวคลื่นมีส่วนสัมพันธ์กับความถี่ของคลื่นดังนี้

C =

=

เมื่อ c คือ ความเร็วของคลื่นแม่เหล็กไฟฟ้าในสูญญากาศ หรือความเร็วแสงในสูญญากาศ

c = 2.99 x 108ms-1หรือ โดยประมาณ c = 3.0 x 108ms-1

จากความสัมพันธ์ของความยาวคลื่นของความยาวคลื่นแม่เหล็กไฟฟ้า ทำให้สามารถเขียนกฎของพลังค์ เพื่อแสดงความสัมพันธ์ระหว่างพลังงานของคลื่นแม่เหล็กไฟฟ้ากับความยาว และความถี่ของคลื่น ได้ดังนี้

E = h = h

เนื่องจากแสงขาวประกอบด้วยแสงสีต่าง ๆ รวม 7 สี แต่ละสีมีลักษณะเป็นแถบสเปกตรัมจึงมีความยาวคลื่นเป็นช่วง ดังนั้นค่าของความถี่และพลังงานจึงเป็นช่วงด้วย การคำนวณเกี่ยวกับพลังงานของคลื่นจึงต้องระบุความยาวคลื่นหรือความถี่ที่แน่นอนด้วย เช่น แสงสีเขียวมีความยาวคลื่นระหว่าง 490 - 580 จะมีพลังงานอยู่ระหว่าง 4.06 x 10-19และ 3.43 x 10-19จูล ถ้าแสงสีเขียวที่มีความยาวคลื่น 520 nm จะมีพลังงาน 3.82 x 10-19จูล เป็นต้น

ตารางที่5 พลังงาน ความยาว และความถี่ของแสงสีขาว

จากตารางจะเห็นได้ว่าในแสงขาวซึ่งมีสีต่าง ๆ รวม 7 สี แสงสีม่วงจะมีความยาวคลื่นสั้นที่สุด แต่มีความถี่สูงสุด และมีพลังงานสูงสุด ในขณะที่แสงสีแดงมีความยาวคลื่นมากที่สุด แต่มีความถี่ต่ำสุดและมีพลังงานต่ำที่สุด

หรือพิจารณาจากสูตร E = h= h

ถ้า มาก และ E จะน้อย

แต่ถ้า น้อย และ E จะมาก

ตัวอย่างเพิ่มเติมที่ 1เส้นสเปกตรัมของไฮโดรเจน 2 เส้น คือเส้นสีม่วงมีความยาวคลื่น 410 nm และเส้นสีน้ำเงินมีความยาวคลื่น 434 nm จะมีพลังงานต่างกันเท่าใด ?

วิธีทำจากสูตร E = h = h

c = 3.0 x 108m/s

h = 6.625 x 10-34Js

สำหรับเส้นสีม่วง ; = 410 nm = 4.10 x 10-7m

E = 6.625 x 10-34Js x = 4.85 x 10-19J

สำหรับเส้นสีม่วง ; = 434 nm = 4.34 x 10-7m

E = 6.625 x 10-34Js x

= 4.58 x 10-19J

มีพลังงานต่างกันเท่ากับ 4.85 x 10-19J - 4.58 x 10-19J = 2.7 x 10-20J

ตัวอย่างเพิ่มเติมที่ 2ธาตุชนิดหนึ่งเมื่อนำไปเผาไฟ จะเกิดเส้นสเปกตรัมหลายเส้น จากการทดลองพบว่าเส้นสเปกตรัมเส้นหนึ่งมีพลังงาน 4.0 x 10-19J สเปกตรัมเส้นดังกล่าวจะมีความยาวและความถี่คลื่นเป็นเท่าใด และมีสีอะไร

วิธีทำE = h

E = 4.0 x 10-19J

h = 6.625 x 10-34Js

c = 2.998 x 108m/s

จะได้ 4.0 x 10-19J = 6.625 x 10-34Js x

= 497 x 10-9m = 497 nm

จาก =

=

= 6.04 x 1014Hz

สเปกตรัมเส้นนี้มีความยาวคลื่น 497 นาโนเมตร ความถี่ 6.04 x 1014Hz และตรงกับสีเขียว (ช่วงสีเขียวอยู่ระหว่างความยาวคลื่น 490 - 580 นาโนเมตร)

บทเรียนที่ 9 การอธิบายการเกิดสเปกตรัม

การอธิบายการเกิดสเปกตรัม

เนื่องจากแบบจำลองอะตอมที่โปรตอนและนิวตรอนรวมกันเป็นนิวเคลียส มีอิเล็กตรอนวิ่งอยู่รอบ ๆ นิวเคลียส สามารถอธิบายได้แต่เพียงว่าทำไมโปรตอนจึงอยู่รวมกันเป็นนิวเคลียสได้ แต่ไม่สามารถอธิบายได้ว่าทำไมอิเล็กตรอน ซึ่งมีประจุเป็นลบเหมือนกัน จึงอยู่รวมกันรอบ ๆ นิวเคลียส ไม่ได้บอกให้ทราบว่าอิเล็กตรอนทั้งหมดเหล่านั้นอยู่ในที่เดียวกัน หรือแบ่งเป็นกลุ่ม ๆ อย่างไร และเมื่อมีการศึกษาการเผาสารซึ่งพบว่าสารประกอบที่มีโลหะต่างกัน จะให้สีของเปลวไฟต่างกัน แบบจำลองนี้ ไม่สามารถอธิบายได้ว่า สีของเปลวไฟนั้นเกิดขึ้นจากอะไร เกิดขึ้นได้อย่างไร โดยเฉพาะอย่างยิ่งเมื่อศึกษาสีของเปลวไฟด้วยสเปกโตรสโคปซึ่งจะเห็นเป็นเส้นสเปกตรัมที่มีสีต่าง ๆ กัน แบบจำลองนี้ก็ไม่สามารถอธิบายได้เช่นเดียวกัน แสดงว่าแบบจำลองนี้ยังไม่ถูกต้อง นักวิทยาศาสตร์จึงพยายามสร้างแบบจำลองอะตอมใหม่ขึ้นมาเพื่อใช้อธิบายปรากฎการณ์ดังกล่าว

การศึกษาสีของเปลวไฟที่เกิดขึ้นจากการเผาสาร มักจะเห็นเพียงสีเดียว เห็นเด่นชัดที่สุด ทั้งนี้เนื่องจากตาของคนไม่สามารถที่จะแยกสีที่มีความถี่ต่าง ๆ ที่ผสมกันอยู่ออกจากกันได้ จึงมองเห็นเฉพาะสีที่เด่นชัดที่สุดเพียงสีเดียวเท่านั้น แต่ถ้าใช้สเปกโตรสโคปซึ่งเป็นเครื่องมือแยกสีตามความถี่ของแสง จะเห็นเป็นเส้นที่มีสีต่าง ๆ กันหลายเส้นซึ่งเรียกว่า เส้นสเปกตรัม แต่อย่างไรก็ตามเส้นสเปกตรัมที่เด่นชัดมีความเข้มของสีมากที่สุด จะเป็นสีเดียวกับที่มองเห็นด้วยตาเปล่า

ถ้าเปรียบเทียบเทียบสเปกตรัมของสารต่าง ๆ กับสเปกตรัมของแสงอาทิตย์และแสงจากหลอดฟลูออเรสเซนต์จะพบว่า สเปกตรัมที่เห็นจากแสงอาทิตย์มีลักษณะเป็นแถบที่มีแสงสีเจ็ดสีต่อเนื่องกัน ที่เรียกว่าสเปกตรัมแบบต่อเนื่อง เนื่องจากเป็นสเปกตรัมของแสงขาวนั่นเอง สำหรับสเปกตรัมของหลอดฟลูออเรสเซนต์นอกจากจะเห็นเป็นแถบสีแบบสเปกตรัมของแสงขาวเป็นพื้นแล้ว ยังมีเส้นปรากฏในแถบสเปกตรัมด้วย เรียกว่าเส้นสเปกตรัม ซึ่งจัดว่าเป็นสเปกตรัมที่ไม่ต่อเนื่อง เส้นสเปกตรัมที่เห็นเด่นชัดที่สุดคือ เส้นสีเขียว ซึ่งเกิดจากธาตุที่บรรจุไว้ในหลอด

ฟลูออเรสเซนต์นั้น ลักษณะของเส้นสเปกตรัมจะคล้ายกับสเปกตรัมที่ได้จากการเผาสาร

สำหรับลักษณะของสเปกตรัมหรือสีของเปลวไฟของสารประกอบต่าง ๆที่เกิดจากโลหะชนิดเดียวกัน จากตารางที่ผ่านมาจะเห็นได้ว่าได้เส้นสเปกตรัมที่มีลักษณะเหมือนกันทุกประการทั้งตำแหน่งของเส้นสเปกตรัม ถึงแม้ว่าจะมีอโลหะต่างชนิดกัน เช่น กรณีของสารประกอบโซเดียม ไม่ว่าจะเป็น NaCl หรือ Na2SO4จะเห็นสีของเส้นสเปกตรัมที่เด่นชัดที่สุดเป็นสีเหลองเข้มเหมือนกัน อยู่ในตำแหน่งเดียวกัน หรือมีความยาวคลื่นเท่ากัน ทั้ง ๆ ที่สารประกอบโซเดียมนั้นมีอโลหะต่างกันคือ Cl-กับ SO42-แสดงว่าเส้นสเปกตรัมนั้นไม่ได้เกิดจากอโลหะ ถ้าเกิดจากอโลหะสีหรือตำแหน่งของเส้นสเปกตรัมของ NaCl หรือ Na2SO4ควรจะต่างกัน สำหรับสเปกตรัมของสารประกอบคู่อื่น ๆ ที่มีโลหะชนิดเดียวกันและมีอโลหะต่างชนิดกันก็ให้ผลเช่นเดียวกันกับกรณีของเกลือโซเดียม คือให้สเปกตรัมเหมือนกันเมื่อเป็นโลหะชนิดเดียวกัน ดังนั้นจึงสรุปได้ว่า “ เส้นสเปกตรัมเกิดจากอะตอมส่วนที่เป็นโลหะไม่ได้เกิดจากส่วนที่เป็นอโลหะ”

เนื่องจากลักษณะของเส้นสเปกตรัมขึ้นอยู่กับชนิดของโลหะ โลหะชนิดเดียวกันจะให้สเปกตรัมที่เหมือนกัน และแตกต่างจากสเปกตรัมของโลหะอื่น ๆ สเปกตรัมของธาตุชนิดต่าง ๆ จะมีลักษณะเป็นแบบเฉพาะตัวทั้งตำแหน่ง สี และจำนวนเส้นสเปกตรัม สเปกตรัมของโลหะชนิดเดียวกัน ไม่ว่าโลหะนั้นจะเป็นธาตุบริสุทธิ์หรืออยู่ในรูปของสารประกอบจะต้องมีลักษณะเหมือนกัน คือ มีจำนวนเส้นของสเปกตรัมเท่ากัน แต่ละเส้นมีสีเดียวกัน(อาจจะมีความเข้มของสีไม่เท่ากัน) และตำแหน่งของเส้นสเปกตรัมแต่ละเส้นจะต้องเหมือนกัน ถ้าเป็นสเปกตรัมของโลหะต่างชนิดกันจะต้องไม่เหมือนกัน สีของสเปกตรัมและจำนวนเส้นของสเปกตรัมอาจจะเหมือนกัน แต่ตำแหน่งของเส้นสเปกตรัมทั้งหมดจะต้องไม่ตรงกัน การที่สเปกตรัมเป็นสมบัติเฉพาะตัวของธาตุ ทำให้สามารถนำมาใช้ในแง่ของการวิเคราะห์ชนิดของธาตุได้ เช่น หาสเปกตรัมของแร่ต่าง ๆ เปรียบเทียบกับสเปกตรัมของธาตุที่รู้จักดีอยู่แล้วเพื่อจะวิเคราะห์ได้ว่าแร่นั้นประกอบด้วยธาตุอะไรบ้าง

สเปกตรัมไม่ได้เกิดเฉพาะจากโลหะอย่างเดียวเท่านั้น อโลหะก็ให้สเปกตรัมเช่นเดียวกัน แต่เป็นสเปกตรัมที่เกิดในช่วงของความถี่ที่ตาเรามองไม่เห็น

โดยสรุป

1. สเปกตรัมเป็นสมบัติเฉพาะตัวของธาตุชนิดหนึ่ง ๆ ซึ่งแตกต่างจากธาตุชนิดอื่น

2. สเปกตรัมของโลหะชนิดเดียวกันไม่ว่าจะอยู่ในรูปของธาตุบริสุทธิ์หรือในสารประกอบจะต้องมีลักษณะเหมือนกันทั้งหมด ทั้งในแง่ของจำนวนเส้นสเปกตรัม สีของแต่ละเส้น (อาจจะมีสีเข้มไม่เท่ากัน) และ ตำแหน่งของเส้นสเปกตรัม

3. สเปกตรัมของโลหะต่างชนิดกันจะไม่เหมือนกัน สีของเส้นสเปกตรัมอาจจะเหมือนกัน แต่ตำแหน่งของเส้นสเปกตรัมทั้งหมดจะไม่ตรงกัน

สำหรับสารที่อยู่ในสถานะก๊าซก็สามารถจะตรวจดูสเปกตรัมได้เช่นเดียวกันแต่ไม่ใช่โดยการนำก๊าซมาเผาเหมือนกับสเปกตรัมของโลหะ สเปกตรัมของก๊าซจะทำได้โดยนำก๊าซมาบรรจุในหลอดแก้วโดยทำให้มีความดันต่ำและใช้พลังงานจากไฟฟ้าแทนการเผา เมื่อก๊าซที่บรรจุอยู่ในหลอดแก้วได้รับพลังงานเพียงพอก็จะเเรืองแสงให้สีต่าง ๆ ซึ่งตาของคนไม่สามารถจะบอกความแตกต่างได้ แต่ถ้าใช้สเปกโตรสโคปส่องดูจะเห็นเป็นเส้นสเปกตรัม เช่นเดียวกับสเปกตรัมของโลหะ ก๊าซแต่ละชนิดจะให้เส้นสเปกตรัมที่มีลักษณะไม่เหมือนกัน

เมื่อเผาสารประกอบของโลหะต่างชนิดกัน จะได้เปลวไฟที่มีสีต่าง ๆ กัน สีของเปลวไฟก็คือส่วนของพลังงานที่แปรรูปมาจากพลังงานความร้อนนั่นเอง แสดงว่าหลังจากที่สารได้รับความร้อนเข้าไปแล้วจะมีการคายพลังงานส่วนหนึ่งออกมาในรูปของแสง การที่มีสีต่าง ๆ กันแสดงว่า พลังงานที่คายออกมานั้นมีค่าไม่เท่ากัน พลังงานที่คายออกมาจะมีส่วนเกี่ยวข้องกับความถี่หรือความยาวของคลื่นแสง ตามกฎของ พลังค์ ถ้าโลหะนั้นคายพลังงานออกมาตรงกับความถี่ของแสงสีใด จะเห็นเป็นเปลวไฟสีนั้น ซึ่งถ้าดูจากสเปกโตรสโคปก็จะเห็นเป็นเส้นสีสเปกตรัมที่มีสีเดียวกัน เนื่องจากการเกิดสเปกตรัมขึ้นอยู่กับพลังงานที่คายออกมา ดังนั้นการอธิบายการเกิดสเปกตรัมจึงต้องตั้งอยู่บนสมมติฐานที่ว่า อะตอมจะต้องมีโครงสร้างที่สามารถรับพลังงานและคายพลังงานได้

นักวิทยาศาสตร์ได้พยายามนำแบบจำลองอะตอมต่าง ๆ ที่มีอยู่มาอธิบายการเกิดสเปกตรัมของธาตุแต่ปรากฏว่าไม่ได้ผล จึงคิดว่าแบบจำลองอะตอมที่มีอยู่นั้นยังไม่ถูกต้อง จะต้องมีการแก้ไขและเพิ่มเติมบางสิ่งบางอย่างเพื่อให้นำมาอธิบายการเกิดสเปกตรัมได้ ดังนั้นจึงสร้างสมมติฐานเกี่ยวกับแบบจำลองอะตอมขึ้นมาใหม่ โดยให้โครงสร้างของอะตอมสามารถที่จะมีการถ่ายเทพลังงานได้ คือให้อะตอมเป็นทรงกลมประกอบด้วยโปนตอนและนิวตรอนรวมกันเป็นนิวเคลียส และมีอิเล็กตรอนโคจรอยู่รอบ ๆ ซึ่งอิเล็กตรอนที่โคจรอยู่นี้กระจายอยู่รอบ ๆ นิวเคลียสในระยะต่างกัน

ทั้งนี้กำหนดลักษณะของอะตอมดังนี้

1. อะตอมแบ่งออกเป็นชั้น ๆ แต่ละชั้นจะมีพลังงานประจำตัวซึ่งมีค่าไม่เท่ากัน เรียกว่ามีระดับพลังงานต่างกัน ระดับพลังงานภายในอะตอมจะเป็นช่วง ๆ ไม่ต่อเนื่อง

2. ระดับพลังงานที่อยู่ใกล้นิวเคลียสมากที่สุดจะมีพลังงานต่ำสุด (คือ E1) เรียกว่าระดับพลังงานในสภาวะพื้น (ground state) ระดับพลังงานที่ต่ออกไปอีก คือ E2, E3, . …. จะมีพลังงานสูงขึ้นตามลำดับ ระดับพลังงานนอกสุดของอะตอมจะมีพลังงานในตัวสูงสุด

ตั้งแต่ระดับพลังงาน E2, E3, . …. เป็นต้นไป เรียกรวมกันว่า Allowed state energy

3. อิเล็กตรอนที่กระจายอยู่ในระดับพลังงานเหล่านี้จะต้องมีพลังงานในตัวเท่ากับพลังงานประจำระดับนั้นจึงจะอยู่ในสภาวะที่เสถียร และสามารถโคจรอยู่ในระดับพลังงานนั้นได้ เช่น อิเล็กตรอนที่จะโคจรอยู่ในระดับพลังงานที่ 1 จะต้องมีพลังงาน E1และอิเล็กตรอนที่อยู่ในระดับพลังงานที่ 2 จะต้องมีพลังงาน E2เป็นต้น ถ้าอิเล็กตรอนมีพลังงานเปลี่ยนไปจากเดิมจะทำให้ไม่เสถียร เช่น อิเล็กตรอนที่อยู่ในระดับ E1เมื่อได้รับพลังงานเพิ่มขึ้นจะขึ้นไปอยู่ในชั้น E2, E3, . …. ซึ่งทำให้ไม่เสถียร อิเล็กตรอนจะพยายามกลับมาสู่ตำแหน่งเดิมเพื่อให้อยู่ในภาวะที่เสถียรตามเดิม โดยการคายพลังงานส่วนหนึ่งออกมา

พลังงานของอิเล็กตรอนซึ่งเคลื่อนที่อยู่รอบ ๆ นิวเคลียสประกอบด้วยพลังงานศักย์ (คือพลังงานที่เกิดจากแรงดึงดูดระหว่างอิเล็กตรอนกับโปรตอนหรือกับนิวเคลียส) และพลังงานจลน์ (คือ พลังงานที่เกิดจากการเคลื่อนที่ของอิเล็กตรอน) ปกติอนุภาคทุกชนิดจะอยู่ในภาวะที่เสถียรที่สุดเมื่อมีพลังงานในตัวต่ำที่สุด ดังนั้นในภาวะปกติผลรวมของพลังงานทั้งสองชนิดของอิเล็กตรอนจะมีค่าต่ำสุด (สมมติให้เป็น E1ซึ่งก็คือพลังงานในสภาวะพื้น(ground state)นั่นเอง เมื่อมีการเผาหรือใสไฟฟ้าเข้าไป อะตอมจะได้รับพลังงานเพิ่มขึ้น ทำให้อิเล็กตรอนมีพลังงานสูงขึ้นสมมติให้เป็น E2ซึ่งเรียกว่า “ภาวะกระตุ้น Excited state energy”ในภาวะที่ถูกกระตุ้นนี้อิเล็กตรอนจะมีพลังงานสูงขึ้น ซึ่งทำให้ไม่เสถียร และจะพยายามปรับตัวกลับเข้าสู่ภาวะปกติดังเดิม ในการกลับคืนสู่ภาวะปกติ หรือภาวะพื้นตามเดิมนั้น อิเล็กตรอนจะต้องคายพลังงานออกมาเท่ากับพลังงานที่ได้รับเข้าไป พลังงานจำนวนนี้จะเท่ากับผลต่างของพลังงานทั้งสองระดับ

ถ้าให้ DE = พลังงานที่อิเล็กตรอนคายออกหรือได้รับเข้าไป

DE = E2- E1

พลังงานที่อิเล็กตรอนคายออกมา (DE) ส่วนใหญ่จะปรากฏอยู่ในรูปของพลังงานแสงเป็นเส้นสเปกตรัมที่มีสีต่าง ๆ ถ้าอิเล็กตรอนมีเพียง 2 ระดับพลังงาน เส้นสเปกตรัมควรจะปรากฏเป็นเส้นเดียว แต่จากการพิจารณาเส้นสเปกตรัมของธาตุต่าง ๆ พบว่ามีมากกว่า 1 เส้น ทั้งสิ้น เช่น ธาตุไฮโดรเจนมีเส้นสเปกตรัมที่ปรากฏอยู่ในช่วงแสงขาวถึง 4 เส้นด้วยกัน แต่ละเส้นจะมีความยาวคลื่นและพลังงานแตกต่างกันดังในตารางต่อไปนี้

ตารางที่6 ความยาวคลื่นและพลังงานของเส้นสเปกตรัมของไฮโดรเจน

พลังงานที่อิเล็กตรอนดูดและคายออกในการเปลี่ยนระดับพลังงาน

การที่ไฮโดรเจนมีเส้นสเปกตรัมให้เห็นถึง 4 เส้น แสดงว่าภายในอะตอมจะต้องไม่ได้มีเพียง 2 ระดับพลังงานเท่านั้น แต่คงจะต้องมีมากกว่านี้ และการที่ความยาวคลื่นไม่ได้ต่อเนื่องกัน แสดงว่าระดับพลังงานในอะตอมควรจะเป็นช่วงไม่ต่อเนื่องกัน ระดับพลังงานในอะตอมของไฮโดรเจนจะต้องมีระดับที่ 3, 4, …. ต่อ ๆ ไป ซึ่งจัดเป็นชั้น ๆ การที่มีระดับพลังงานหลายระดับ แต่ละระดับมีค่าพลังงานคงที่ทำให้ผงต่างระหว่างระดับพลังงานคู่หนึ่ง ๆ มีค่าไม่เท่ากัน แต่เป็นค่าคงที่เช่น DE = E2- E1

DE = E3- E1

DE = E4- E1

เมื่อผลต่างของระดับพลังงานคู่หนึ่ง ๆ มีค่าไม่เท่ากัน พลังงานในส่วนที่คายออกมาจึงมีค่าไม่เท่ากันด้วย ทำให้มีเส้นสเปกตรัมได้หลายเส้น ดังในรูปต่อไปนี้

เมื่ออิเล็กตรอนได้รับพลังงานเพิ่มขึ้นจนขึ้นไปอยู่ในระดับ E2, E3,E4และ E5ซึ่งอยู่ในภาวะที่ถูกกระตุ้นทำให้ไม่เสถียร อิเล็กตรอนจะปรับตัวให้กลับสู่ภาวะที่เสถียรตามเดิม โดยเปลี่ยนจากระดับพลังงานสูงาสู่ระดับพลังงานต่ำ (E1) ซึ่งจะคายพลังงานออกมาจำนวนหนึ่ง

เช่น อิเล็กตรอนจากระดับ E2กลับสู่ระดับ E1จะคายพลังงาน DE1

ตามกฎของพลังค์ พลังงานจะมีส่วนสัมพันธ์กับความยาวคลื่นคือ

DE1= E2- E1= hu1=

ดังนั้นพลังงานส่วนที่คายออกมาจะมีความยาวคลื่น l1ซึ่งในกรณีของไฮโดรเจน l1= 656 nm ตรงกับความยาวคลื่นของสีแดง จึงทำให้เห็นเป็นเส้นสเปกตรัมสีแดงที่ 656 nm

สำหรับการเปลี่ยนระดับพลังงานของอิเล็กตรอนจาก E3,E4และ E5มายัง E1ก็เช่นเดียวกัน DE2= E3- E1= hu2=

DE3= E3- E1= hu3=

DE4= E4- E1= hu4=

l2จะตรงกับความยาวคลื่น 486 nm ซึ่งเป็นความถี่ของสี้น้ำทะเล

l3จะตรงกับความยาวคลื่น 434 nm ซึ่งเป็นความถี่ของสี้น้ำเงิน

l4จะตรงกับความยาวคลื่น 410 nm ซึ่งเป็นความถี่ของสี้แดง

ดังนั้น จึงเห็นสเปกตรัมรวม 4 เส้นดังกล่าว

สีของเส้นสเปกตรัมเส้นต่างๆ จะมีความเข้มไม่เท่ากัน ซึ่งแสดงว่าการเปลี่ยนแปลงพลังงานในระดับต่าง ๆ มีความถี่ในการเกิดไม่เท่ากัน การเปลี่ยนแปลงพลังงานในช่วงใดที่เกิดมาก ความเข้มข้นของสีก็จะเข้มมาก เช่น ถ้าสีน้ำทะเลมีความเข้มของสีเห็นเด่นชัดที่สุดแสดงว่าการเปลี่ยนแปลงที่ระดับ DE2(ความยาวคลื่น 486 nm) มีความถี่มากที่สุด

เมื่อพิจารณาผลต่างระหว่างพลังงานของระดับพลังงานคู่ที่อยู่ถัดกันของเส้นสเปกตรัมของไฮโดรเจนจะได้ดังนี้

ตารางที่7 ผลต่างระหว่างพลังงานของเส้นสเปกตรัมของไฮโดรเจน

จะเห็นว่าผลต่างระหว่างพลังงานของระดับพลังงานคู่ที่อยู่ถัดกันแต่ละคู่ ไม่เท่ากัน ความแตกต่างจะน้อยลงตามลำดับ เมื่อระดับพลังงานสูงขึ้น กล่าวได้ว่า ระดับพลังงานยิ่งสูงขึ้นจะยิ่งอยู่ชิดกันมากขึ้น ดังในรูปที่ 3 แสดงแผนผังการเปลี่ยนระดับพลังงานของอิเล็กตรอนของไฮโดรเจน

สรุปการเกิดสเปกตรัมของธาตุ

1.เมื่ออิเล็กตรอนได้รับพลังงานจะถูกกระตุ้นให้ขึ้นไปอยู่ระดับพลังงานที่สูงขึ้นซึ่งจะขึ้นไปอยู่ระดับใดย่อมขึ้นกับปริมาณพลังงานที่ได้รับ การที่อิเล็กตรอนขึ้นไปอยู่ในระดับพลังงานที่สูงขึ้นนี้ทำให้อะตอมไม่เสถียร อิเล็กตรอนจึงพยายามกลับมาสู่ระดับพลังงานเดิมโดยการคายพลังงานออกมาค่าหนึ่งซึ่งเท่ากับพลังงานที่ได้รับเข้าไป พลังงานส่วนใหญ่ที่คายออกมาจะอยู่ในรูปของคลื่นแม่เหล็กไฟฟ้า ซึ่งปรากฎเป็นเส้นสเปกตรัมที่มีสีต่าง ๆ กันในสเปกโตรสโคป

2.การเปลี่ยนระดับพลังงานของอิเล็กตรอนไม่จำเป็นจะต้องเกิดระหว่างระดับพลังงานที่อยู่ถัดกัน แต่อาจจะมีการเปลี่ยนข้ามขั้นได้ จึงเป็นเป็นเหตุให้มีเส้นสเปกตรัมเกิดขึ้นได้หลายเส้น

3.ภายในอะตอมซึ่งแบ่งพลังงานเป็นชั้น ๆ ระดับพลังงานที่อยู่ใกล้นิวเคลียสจะต่ำที่สุด และระดับพลังงานที่อยู่ห่างจากนิวเคลียสมากที่สุดจะมีค่าสูงสุด ดังนั้นอิเล็กตรอนในระดับพลังงานต่ำจึงอยู่ใกล้นิวเคลียสมากกว่าอิเล็กตรอนในระดับพลังงานสูง

4.ระดับพลังงานต่ำ ๆ จะอยู่ห่างกัน และเมื่อสูงขึ้นจะอยู่ชิดกันมากขึ้น กล่าวคือ ยิ่งระดับพลังงานสูงขึ้นจะยิ่งอยู่ชิดกันมากขึ้น

5.เส้นสเปกตรัมของธาตุ แสดงให้เห็นถึงพลังงานที่อิเล็กตรอนคายออกมาเมื่อเปลี่ยนจากระดับพลังงานสูงมาสู่ระดับพลังงานที่ต่ำกว่า

บทเรียนที่ 10 หลักการจัดอิเล็กตรอนในระดับพลังงานย่อย

การศึกษาสเปกตรัมของธาตุต่างๆ อย่างละเอียด พบว่า ระดับพลังงานของอิเล็กตรอนที่โคจรอยู่รอบๆ นิวเคลียสยังแบ่งออกเป็นระดับพลังงานย่อย(Subshell)

ระดับพลังงานย่อย (Subshell)อีกชื่อหนึ่งคือ ออร์บิทัล (Orbital) ซึ่งเป็นอาณาเขตและรูปร่างใน 3 มิติ บริเวณรอบนิวเคลียส ซึ่งมีโอกาสสูงที่จะพบอิเล็กตรอนที่มีพลังงานเฉพาะ ระดับพลังงานย่อย เป็นระดับพลังงานย่อยที่อยู่ในแต่ละระดับพลังงานหลัก โดยระดับพลังงานย่อยมี 4 ประเภทใหญ่ คือs , p , d ,fและแต่ละชนิดก็จะมีรูปร่างต่างกัน ดังรูป

โดย sมาจากคำว่า sharp

Pมาจากคำว่า principal

dมาจากคำว่า diffuse

fมาจากคำว่า fundamental

จำนวนระดับพลังงานย่อยในแต่ละระดับพลังงาน ตั้งแต่ระดับพลังงานที่ 1 – 5 เป็นดังนี้

ระดับพลังงานที่ 1 มี 1 ระดับพลังงานย่อย คือ 1s

ระดับพลังงานที่ 2 มี 2 ระดับพลังงานย่อย คือ 2s2p

ระดับพลังงานที่ 3 มี 3 ระดับพลังงานย่อย คือ 3s3p3d

ระดับพลังงานที่ 4 มี 4 ระดับพลังงานย่อย คือ 4s4p4d4f

ระดับพลังงานที่ 5 มี 5 ระดับพลังงานย่อย คือ 5s5p5d5f

ตัวเลขข้างหน้าแสดงระดับพลังงานหลัก (n) ของอะตอม ระดับพลังงานย่อยที่อยู่ในระดับพลังงานเดียวกันมีค่าพลังงานแตกต่างกัน และในแต่ละระดับพลังงานย่อยจะมีจำนวนออร์บิทัลแตกต่างกัน

ระดับพลังงานย่อยsมี 1 ออร์บิทัล

ระดับพลังงานย่อยpมี 3 ออร์บิทัล

ระดับพลังงานย่อยdมี 5 ออร์บิทัล

ระดับพลังงานย่อยfมี 7 ออร์บิทัล

แต่ละออร์บิทัลมีจำนวนอิเล็กตรอนสูงสุด2 อิเล็กตรอนจำนวนอิเล็กตรอนสูงสุดในแต่ละระดับพลังงานย่อยจึงขึ้นอยู่กับจำนวนออร์บิทัลดังนี้

ระดับพลังงานย่อยsมี 1 ออร์บิทัล มีจำนวนอิเล็กตรอนได้สูงสุด 2 อิเล็กตรอน

ระดับพลังงานย่อยpมี 3 ออร์บิทัล มีจำนวนอิเล็กตรอนได้สูงสุด 6 อิเล็กตรอน

ระดับพลังงานย่อยdมี 5 ออร์บิทัล มีจำนวนอิเล็กตรอนได้สูงสุด 10 อิเล็กตรอน

ระดับพลังงานย่อยfมี 7 ออร์บิทัล มีจำนวนอิเล็กตรอนได้สูงสุด 14 อิเล็กตรอน

การจัดเรียงอิเล็กตรอนในระดับพลังงานย่อย มีหลักการดังนี้

1. ต้องการบรรจุในออร์บิทัลที่มีพลังงานต่ำสุดที่ยังว่างอยู่ก่อน เช่น 1s2s2p3s…..ตามลำดับ

โดยพิจารณาจากแผนภาพ

2. อิเล็กตรอนสองอิเล็กตรอนที่อยู่ในออร์บิทัลเดียวกัน มีทิศทางการหมุนรอบตัวเองตรงข้ามกัน โดยตัวหนึ่งหมุนตามเข็มนาฬิกาและอีกตัวหนึ่งหมุนทวนเข็มนาฬิกา ให้แทน ออร์บิทัล และ แทนอิเล็กตรอน ดังนั้น การเขียนอิเล็กตรอนในออร์บิทัลเขียนแทนด้วย หรือ เมื่อมีอิเล็กตรอน 2 ตัวอยู่ในออร์บิทัลเดียวกันจะเขียนเป็น ตามกลักการกีดกันของเพาลี

3. การบรรจุอิเล็กตรอนในออร์บิทัลซึ่งอยู่ในระดับพลังงานต่างๆมีหลักการดังนี้

3.1 ต้องการบรรจุในออร์บิทัลที่มีพลังงานต่ำสุดที่ยังว่างอยู่ก่อน เช่น 1s2s2p3s…..ตามลำดับ

3.2 ในกรณีที่มีหลายออร์บิทัลและแต่ละออร์บิทัลมีพลังงานเท่ากัน ให้บรรจุอิเล็กตรอนในลักษณะที่ทำให้

เป็นอิเล็กตรอนเดี่ยวมากที่สุดเท่าที่จะมากได้(ตามกฎของอุนด์) ถ้ามีอิเล็กตรอนเหลือจึงบรรจุอิเล็กตรอนเป็นคู่เต็มออร์บิทัล เช่น ถ้ามี 2 อิเล็กตรอนในออร์บิทัล p จะบรรจุอิเล็กตรอนได้เป็น

ถ้ามี 4 อิเล็กตรอนในออร์บิทัล p จะบรรจุอิเล็กตรอนได้เป็น

1.3 อะตอมของธาตุที่มีการบรรจุอิเล็กตรอนเต็ม ในทุกๆออร์บิทัลที่มีระดับพลังงานเท่ากัน เรียกว่า การบรรจุเต็มถ้ามีอิเล็กตรอนอยู่เพียงครึ่งเดียวเรียกว่าการบรรจุครึ่งอะตอมที่มีการบรรจุอิเล็กตรอนแบบบรรจุเต็มและบรรจุครึ่งจะมีความเสถียรมากกว่าการบรรจุแบบอื่นๆ

การบรรจุเต็ม

การบรรจุครึ่ง

3.4 สัญลักษณ์แสดงการจัดอิเล็กตรอนในออร์บิทัล เขียนได้โดยใช้ตัวเลขแสดงระดับพลังงานตามด้วยตัวอักษรแสดงระดับพลังงานย่อย และเขียนเลขยกกำลังบนตัวอักษร เพื่อแสดงจำนวนอิเล็กตรอนในออร์บิทัล เช่น1s2โดย 1 คือ ระดับพลังงานหลักที่ 1sคือระดับพลังงานย่อย และ 2 อิเล็กตรอนที่บรรจุอยู่ในออร์บิทัล 1s

3.5. อิเล็กตรอนที่อยู่ในระดับพลังงานสูงสุดหรือสูงสุดหรือชั้นนอกสุดของอะตอมเรียกว่าเวเลนซ์อิเล็กตรอน

บทเรียนที่ 11 วิวัฒนาการของการสร้างตารางธาตุ

ความหมายของตารางธาตุ

ตารางธาตุ (Periodic Table ) คือตารางที่รวบรวมธาตุต่าง ๆ เข้าเป็นหมวดหมู่ ตามคุณสมบัติที่เหมือน ๆ กัน ไว้เป็นพวกเดียวกัน เพื่อสะดวกในการจดจำและศึกษา

สมบัติของธาตุ

ธาตุ(Element)คือ สารบริสุทธิ์ที่ประกอบด้วยอะตอมเพียงชนิดเดียว เช่น โซเดียม (Na) แมกนีเซียม (Mg) คาร์บอน (C) ออกซิเจน (O) เป็นต้น

ในการจัดธาตุออกเป็นหมวดหมู่จะอาศัยสมบัติที่คล้ายคลึงกันของธาตุแต่ละชนิดเป็นเกณฑ์ เช่น ใช้ความเป็นโลหะและอโลหะเป็นเกณฑ์ แบ่งได้เป็น 3 กลุ่ม คือ โลหะ กึ่งโลหะ และอโลหะ และยังสามารถแบ่งธาตุทั้ง 3 กลุ่มออกเป็นกลุ่มย่อยๆได้อีก เช่น แบ่งกลุ่มย่อยโดยใช้สถานะเป็นเกณฑ์ความว่องไวในการเกิดปฏิกิริยา และลักษณะที่อุณหภูมิปกติ เป็นต้น ดังแผนภาพเราแบ่งธาตุออกเป็น3ชนิดคือ

1. โลหะ(Metal)

2.อโลหะ(Non-metal)

3.กึ่งโลหะ ( Metalloid หรือ Semi metal )

สมบัติของโลหะ

1. มีสถานะเป็นของแข็งที่อุณหภูมิปกติ (ยกเว้นปรอท เป็นของเหลว)
2. มีจุดเดือดและจุดหลอมเหลวสูง
3. แข็งและเหนียวสามารถตีเป็นแผ่นบางๆ หรือดึงให้เป็นเส้นได้
4. นำไฟฟ้าและนำความร้อนได้ดี การนำไฟฟ้าลดลงเมื่ออุณหภูมิสูงขึ้น
5. มีความแตกต่างของอุณหภูมิระหว่างจุดเดือดและจุดหลอมเหลวกว้าง
6. เคาะมีเสียงดังกังวาน
7. ขัดเป็นมันวาว
8. มีความหนาแน่นสูง แต่บางชนิดมีความหนาแน่นต่ำ ได้แก่ โลหะเบา เช่นธาตุหมู่ I A และ II A
9. มีค่า EN ต่ำ จึงเสียอิเล็กตรอนได้ง่ายเกิดเป็นไอออนบวก
10. ทำปฏิกิริยากับกรดเกิดก๊าช ไฮโดรเจน ยกเว้นโลหะมีตระกูล

สมบัติของอโลหะ

1. มีทั้ง 3 สถานะ คือ
2. - ของแข็งเช่น คาร์บอน ( C ) กำมะถัน (S )

-ของเหลว เช่น โบรมีน

- ก๊าช เช่น ไฮโดรเจน ออกซิเจน

1. มีจุดเดือดและจุดหลอมเหลวต่ำ ยกเว้นแกรไฟต์
2. เปราะ แตกง่าย ตีเป็นแผ่นหรือดึงเป็นเส้นไม่ได้
3. ไม่นำไฟฟ้าและความร้อน ยกเว้นแกรไฟต์
4. มีความแตกต่างของอุณหภูมิระหว่างจุดเดือด และจุดหลอมเหลวแคบ
5. เคาะไม่มีเสียงกังวาน
6. ผิวไม่มันวาว
7. มีความหนาแน่นต่ำ
8. มีค่า EN สูง จึงรับอิเล็กตรอนได้ง่ายเกิดเป็นไอออนลบ

การจัดธาตุเป็นหมวดหมู่ของนักเคมียุคต่าง ๆ

ตารางธาตุ หมายถึง ตารางที่นักวิทยาศาสตร์สร้างขึ้นมา เพื่อแบ่งธาตุที่มีสมบัติเหมือนกันออกเป็นหมวดหมู่ เพื่อให้ง่ายแก่การศึกษา โดยแบ่งธาตุทั้งหมดออกเป็นหมู่และคาบ

ธาตุที่อยู่ในแนวดิ่งเดียวกัน เรียกว่า อยู่ในหมู่เดียวกัน

ธาตุที่อยู่ในแนวนอนเดียวกัน เรียกว่า อยู่ในคาบเดียวกัน

ในระหว่างปี พ.ศ. 2346 ถึง 2456 มีธาตุต่าง ๆที่พบในธรรมชาติประมาณ 63 ธาตุ ซึ่งนักวิทยาศาสตร์ได้พยายามจัดธาตุเหล่านี้ให้เป็นหมวดหมู่หรือเป็นตารางธาตุโดยในช่วงแรก ๆ นั้นแบ่งธาตุออกเป็นหมวดหมู่โดยอาศัยสมบัติของธาตุ ทั้งนี้ได้จากการสังเกตพบความคล้ายคลึงกันของสมบัติของธาตุเป็นกลุ่ม ๆ ทำให้นำมาจัดเป็นตารางธาตุได้ เช่นแบ่งกลุ่มโดยอาศัยสมบัติเกี่ยวกับโลหะ-อโลหะ โดยอาศัยสมบัติของความเป็นกรด-เบสของธาตุ เป็นต้น ต่อมาเมื่อหามวลอะตอมของธาตุได้ จึงใช้มวลอะตอมมาประกอบในการจัดตารางธาตุ จนในปัจจุบันจัดตารางธาตุโดยอาศัยการจัดเรียงอิเล็กตรอน

1. ตารางธาตุของเดอเบอไรเนอร์

การจัดตารางธาตุนั้นเริ่มขึ้นตั้งแต่ปี พ.ศ. 2360 (ค.ศ. 1817) โดย โยฮันน์ เดอเบอไรเนอร์ (Johaun Dobereiner) นักเคมีชาวเยอรมัน ได้นำธาตุต่าง ๆ ที่พบในขณะนั้นมาจัดเรียงเป็นตารางธาตุ โดยนำธาตุต่าง ๆ ที่มีสมบัติคล้ายคลึงกันมาจัดไว้ในหมู่เดียวกัน หมู่ละ 3 ธาตุ เรียงตามมวลอะตอมจากน้อยไปมากในแต่ละหมู่ มวลอะตอมของธาตุที่อยู่กลางจะเป็นค่าเฉลี่ยของมวลอะตอมของธาตุที่เหลืออีก 2 อะตอม เรียกว่ากฎชุดสาม(law of triads หรือ Dobereine’s law of triads)

ตารางที่ 8 มวลอะตอมเฉลี่ยของธาตุบางกลุ่มตามกฎชุดสาม

จะเห็นได้ว่ามวลอะตอมเฉลี่ย มีค่าใกล้เคียงกับมวลอะตอมของธาตุกลาง อย่างไรก็ตาม เมื่อนำกฎดังกล่าวไปใช้กับธาตุกลุ่มอื่นที่มีสมบัติคล้ายคลึงกัน ปรากฏว่าไม่มีผลเท่าที่ควร มวลอะตอมของธาตุกลางไม่เท่ากับค่าเฉลี่ยของมวลอะตอมของธาตุที่เหลือ กฎชุดสามของเดอเบอไรเนอร์จึงไม่เป็นที่ยอมรับกันในเวลาต่อมา

2. ตารางธาตุของนิวแลนด์

ในปี พ.ศ. 2407 (ค.ศ. 1864) จอห์น นิวแลนด์ (John Newlands) นักเคมีชาวอังกฤษได้พบว่าเมื่อนำธาตุต่าง ๆ มาเรียงลำดับตามมวลอะตอมจากน้อยไปหามาก ให้เป็นแถวตามแนวนอน สมบัติของธาตุจะมีลักษณะคล้ายกันเป็นช่วง ๆ ซึ่งลักษณะดังกล่าวเกิดขึ้นทุก ๆ ของธาตุที่ 8

เช่น ถ้าเริ่มต้นจากธาตุ Li แล้วเรียงลำดับมวลอะตอมไปถึงธาตุที่ 8 จะตรงกับ Na ซึ่ง Li และ Na มีสมบัติต่าง ๆ คล้ายคลึงกัน

ตารางที่9 ตัวอย่างการจัดตารางธาตุของนิวแลนด์ส์

เรียกกฎการจัดตารางธาตุของนิวแลนด์ส์ว่า law of octaves หรือ Newlands’ law of octaves อย่างไรก็ตาม กฎนี้ไม่เป็นที่ยอมรับกัน เนื่องจากไม่สามารถอธิบายว่าเหตุใดมวลอะตอมจึงมาเกี่ยวข้องกับความคล้ายคลึงดังกล่าว นอกจากกฎนี้แล้วก็ยังใช้ได้กับ ธาตุที่มีมวลอะตอมต่ำ ๆ ไม่เกิน 20 ธาตุแรกเท่านั้น หลังจากนั้นจะใช้กฎนี้ไม่ได้

3. ตารางธาตุของเมนเดเลเอฟ

ในระหว่างปี พ.ศ. 2412 - 2413 (ค.ศ. 1269 - 1270) ยูลิอุส ไมเออร์ (Julius Meyer) นักวิทยาศาสตร์ชาวเยอรมัน และดิมิทรี เมนเดเลเอฟ (Dimitri Mendelejev) นักวิทยาศาสตร์ชาวรัสเซียได้พบในเวลาใกล้เคียงกันว่าสมบัติต่าง ๆ ของธาตุมีส่วนสัมพันธ์กับมวลอะตอมของธาตุกล่าวคือ “ถ้าเรียงลำดับธาตุตามมวลอะตอมจากน้อยไปหามาก จะพบว่าธาตุ ๆ ต่าง จะมีสมบัติคล้ายคลึงกันเป็นช่วง ๆ ” ซึ่งเมเดเลเอฟได้ตั้งเป็นกฎเรียกว่า “กฎพิริออดิก” หรือกฎตารางธาตุ (Periodic law) และพิมพ์เผยแพร่ในปี พ.ศ. 2412 ก่อนที่ไมเออร์จะพิมพ์เผยแพร่ครั้งหนึ่ง ดังนั้นเพื่อเป็นเกียรติแก่เมนเดเลเอฟ จึงเรียกตารางนี้ว่า “ตารางพีริออดิกของเมนเดเลเอฟ” หรือตารางธาตุของเมนเดเลเอฟ (Mendelejev’ s periodic table)

เกณฑ์ที่สำคัญที่เมนเดเลเอฟใช้คือ จัดธาตุที่มีสมบัติคล้ายคลึงกันที่ปรากฏซ้ำกันเป็นช่วง ๆ ให้อยู่ในหมู่หรือในแนวตั้งเดียวกัน และพยายามเรียงลำดับมวลอะตอมจากน้อยไปหามาก ในกรณีที่เรียงตามมวลอะตอมแล้วสมบัติของธาตุไม่สอดคล้องกัน ก็พยายามจัดให้เข้าหมู่โดยปล่อยให้ช่องว่างเว้นไว้ในตารางซึ่งเมนเดเลเอฟคิดว่า ช่องว่างเหล่านั้นน่าจะเป็นตำแหน่งของธาตุซึ่งยังไม่มีการค้นพบในขณะนั้น ในการจัดตารางธาตุนอกจากจะใช้มวลอะตอมแล้ว ยังใช้สมบัติทางเคมีและทางกายภาพของสารประกอบอื่น ๆ นอกเหนือจากสารประกอบคลอไรด์ และออกไซด์มาประกอบการพิจารณาด้วย

ตารางที่10 ตารางพิริออดิกของเมนเดเลเอฟ

ช่องว่างที่เว้นไว้คือตำแหน่งของธาตุที่ยังไม่พบในสมัยนั้น เนื่องจากตำแหน่งของธาตุในตารางธาตุสัมพันธ์กับสมบัติของธาตุ ทำให้เมนเดเลเอฟสามารถทำนายสมบัติของธาตุไว้ล่วงหน้าได้ด้วย โดยการศึกษาสมบัติเกี่ยวกับจุดหลอมเหลว จุดเดือด ความถ่วงจำเพาะ และความร้อนจำเพาะ รวมทั้งสมบัติเกี่ยวกับสารประกอบคลอไรด์ และออกไซด์

ตัวอย่างเช่น ธาตุที่อยู่ในช่องว่างใต้ Si เมนเดเลเอฟเรียกชื่อว่าธาตุเอคาซิลิคอน อีก 15 ปีต่อมาคือในปี พ.ศ. 2429 (ค.ศ. 1886) เคลเมนส์ วิงค์เลอร์ (Clemens Winkler) นักวิทยาศาสตร์ชาวเยอรมันจึงได้พบธาตุนี้และเรียกชื่อว่า ธาตุเจอร์เมเนียม (Ge) นั่นเอง

ตารางที่11 เปรียบเทียบสมบัติของธาตุเอคาซิลิคอนกับเจอร์เมเนียมที่ทำนายและที่ค้นพบ

นอกจากธาตุเอคาซิลิคอนแล้ว ยังมีธาตุอื่นที่เมนเดเลเอฟ ได้เรียกชื่อไว้ล่วงหน้า เช่น

ธาตุที่อยู่ใต้ B เรียกว่า เอคาโบรอน

ธาตุที่อยู่ใต้ Al เรียกว่า เอคาอะลูมิเนียม

ซึ่งปัจจุบันก็คือธาตุ Se และ Ga ตามลำดับ

การจัดตารางธาตุของเมนเดเลเอฟนั้น ถ้ายึดหลักการเรียงตามมวลอะตอมจากน้อยไปหามากอย่างเคร่งครัด จะทำให้ธาตุบางธาตุซึ่งมีสมบัติแตกต่างกันอยู่ในหมู่เดียวกัน ทำให้ต้องยกเว้นไม่เรียงตามมวลอะตอมบ้างแต่เมนเดเลเอฟก็ไม่สามารถให้เหตุผลได้ว่าเป็นเพราะเหตุใดจึงต้องเรียงลำดับธาตุเช่นนั้น เนื่องจากในขณะนั้นยังไม่มีความเข้าใจเกี่ยวกับโครงสร้างของอะตอมไม่มากพอ นักวิทยาศาสตร์ต่อ ๆ มาจึงสร้างแนวคิดใหม่ว่า ตำแหน่งของธาตุในตารางธาตุไม่ควรขึ้นอยู่กับมวลอะตอม แต่ควรจะขึ้นอยู่กับสมบัติอื่น ๆ ที่สัมพันธ์กับมวลอะตอม

4. ตารางธาตุของเฮนรี โมสลีย์

เฮนรี โมสลีย์ (Henry Moseley) นักวิทยาศาสตร์ชาวอังกฤษ ได้แก้ไขตารางธาตุของเมนเดเลเอฟให้ถูกต้องขึ้น โดยการพบว่าเลขอะตอม หรือจำนวนโปรตอนในนิวเคลียสของธาตุ มีความสัมพันธ์กับสมบัติของธาตุมากกว่ามวลอะตอม ทำให้สอดคล้องกับกฎพีริออดิกมากกว่า สามารถสร้างตารางธาตุได้โดยไม่ต้องสลับที่ธาตุบางธาตุเหมือนกรณีการจัดเรียงตามมวลอะตอม

ประมาณปี พ.ศ. 2456 (ค.ศ. 1913) โมสลีย์จึงเสนอตารางธาตุใหม่โดยเรียงตามเลขอะตอมจากน้อยไปหามาก และจัดธาตุที่มีสมบัติคล้ายคลึงกันให้อยู่ในหมู่เดียวกัน และกำหนดกฎตารางธาตุขึ้นใหม่เป็น “สมบัติต่าง ๆ ของธาตุในตารางธาตุขึ้นอยู่กับเลขอะตอมของธาตุ”

ตารางธาตุในปัจจุบัน

เนื่องจากปัจจุบันนักเคมีพบว่า การจัดเรียงตัวของอิเล็กตรอนในอะตอมของธาตุมีส่วนสัมพันธ์กับสมบัติต่าง ๆ ของธาตุ กล่าวคือ ถ้าเรียงลำดับธาตุตามเลขอะตอมจากน้อยไปหามาก จะพบว่าธาตุที่มีสมบัติคล้ายคลึงกันเป็นช่วง ๆ ตามลักษณะของการจัดเรียงอิเล็กตรอนในอะตอมของธาตุนั้น ดังนั้นในปัจจุบันจึงจัดตารางธาตุโดยเรียงตามเลขอะตอมจากน้อยไปมาก ดังในรูปที่ 1.23

รูปที่1.23 ตารางธาตุในปัจจุบัน(ที่มา: www.specialedprep.net/.../compounds1.htm)

ตารางธาตุในรูปที่ 1.23 เป็นแบบที่ใช้กันอยู่มากในปัจจุบัน แบ่งธาตุในแนวตั้งออกเป็น 18 แถวหรือ 18 หมู่ โดยธาตุทั้งหมด 18 แถว แบ่งเป็น 2 กลุ่มใหญ่ ๆ คือกลุ่ม A และ B กลุ่ม A มี 8 หมู่ คือหมู่ IA ถึง VIIIA ส่วนกลุ่ม B ซึ่งอยู่ระหว่างหมู่ IIA และ IIIA มี 8 หมู่เช่นเดียวกัน คือ หมู่ IB ถึง VIIIB (แต่มี 10 แนวตั้ง) เรียกธาตุกลุ่ม B ว่าธาตุทรานซิชัน(Transition Elements)

ธาตุในแต่ละหมู่ ของกลุ่ม A ถ้ามีสมบัติคล้ายกันจะมีชื่อเรียกเฉพาะหมู่ เช่น

* ธาตุหมู่ IA เรียกว่าโลหะอัลคาไล(alkali metal) ได้แก่ Li , Na , K , Rb , Cs , Fr

* ธาตุหมู่ IIA เรียกว่าโลหะอัลคาไลน์เอิร์ท(alkaline earth)ได้แก่ Be Mg Ca Sr Ba Ra

* ธาตุหมู่ VIIA เรียกว่าธาตุเฮโลเจน(halogen) ได้แก่ F Cl Br I At

* ธาตุหมู่ที่ VIIIA เรียกว่าก๊าซเฉื่อย(Inert gas) ได้แก่ He Ne Ar Kr Xe Rn

สำหรับการแบ่งธาตุเป็นคาบ ธาตุทั้งหมดในตารางธาตุแบ่งเป็น 7 คาบ ซึ่งในแต่ละคาบอาจจะมีจำนวนธาตุไม่เท่ากัน เช่น

สำหรับคาบต่าง ๆ ในตารางธาตุแบ่งเป็น 7 คาบดังนี้

* คาบที่ 1 มี 2 ธาตุ คือ H , He

* คาบที่ 2 มี 8 ธาตุ คือ ตั้งแต่ Li ถึง Ne

* คาบที่ 3 มี 8 ธาตุ คือ ตั้งแต่ Na ถึง Ar

* คาบที่ 4 มี 18 ธาตุ คือ ตั้งแต่ K ถึง Kr

* คาบที่ 5 มี 18 ธาตุ คือ ตั้งแต่ Rb ถึง Xe

* คาบที่ 6 มี 32 ธาตุ คือ ตั้งแต่ Cs ถึง Rn

* คาบที่ 7 มี 19 ธาตุ คือ ตั้งแต่ Fr ถึง Ha

รวมทั้งหมด 105 ธาตุ เป็นก๊าซ 11 ธาตุ คือ H , N , O , F , Cl , He , Ne , Ar ,

Kr , Xe และ Rn เป็นของเหลว 5 ธาตุ คือ Cs , Fr , Hg , Ga และ Br ที่เหลือเป็นของแข็ง

สำหรับ 2 แถวล่างเลขอะตอม 57 - 70 และ 89 - 102 เป็นธาตุกลุ่มย่อยที่แยกมาจากหมู่ IIIB ในคาบที่ 6 และ 7 เรียกธาตุในกลุ่มย่อยนี้รวม ๆ ว่ากลุ่มธาตุเลนทาไนด์และกลุ่มธาตุแอกทิไนด์

นอกจากนี้เมื่อพิจารณาธาตุหมู่ IIIA ไปทางขวามือ จะพบเส้นหนักหรือเส้นทึบเป็นแบบขั้นบันได เส้นหนักนี้จะเป็นเส้นแบ่งกลุ่มธาตุโลหะและอโลหะ กล่าวคือ ธาตุทางขวาของเส้นขั้นบันไดจะเป็นอโลหะ ธาตุทางซ้ายมือของเส้นขั้นบันไดจะเป็นโลหะ ธาตุที่อยู่ชิดกับเส้นขั้นบันได เป็นธาตุกึ่งโลหะ ซึ่งมีทั้งสมบัติของโลหะและอโลหะ เช่น ธาตุ B , Si ,Ge ,As , Sb , Te

การตั้งชื่อธาตุที่ค้นพบใหม่

จากตารางธาตุในรูปที่ 1.23 จะพบว่ามีธาตุอยู่ 118 ธาตุ ซึ่งยังมีการค้นพบธาตุใหม่ ๆ เพิ่มขึ้นอีกหลายธาตุ แต่ยังไม่ได้กำหนดสัญลักษณ์ที่แน่นอนไว้ในตารางธาตุ ธาตุบางธาตุถูกค้นพบโดยนักวิทยาศาสตร์หลายคณะ ทำให้มีชื่อเรียกและสัญลักษณ์ต่างกัน

เช่น ธาตุที่ 104 ค้นพบโดยคณะนักวิทยาศาสตร์ 2 คณะ คือ คณะของนักวิทยาศาสตร์สหรัฐอเมริกา ซึ่งเรียกชื่อว่า รัทเทอร์ฟอร์เดียม (Ratherfordium) และใช้สัญลักษณ์ Rf ในขณะที่คณะนักวิทยาศาสตร์สหภาพโซเวียตเรียกชื่อว่าเคอร์ซาโตเวียม(Kurchatovium) ใช้สัญลักษณ์ Ku

ธาตุที่ 105 ค้นพบโดยคณะนักวิทยาศาสตร์ 2 คณะเช่นเดียวกัน คือคณะนักวิทยาศาสตร์สหรัฐอเมริกาเรียกชื่อว่า ฮาห์เนียม (Hahnium) และใช้สัญลักษณ์ Ha ในขณะที่นักวิทยาศาสตร์สหภาพโซเวียตใช้ชื่อว่า นิลส์บอห์เรียม (Neilbohrium) และใช้สัญลักษณ์เป็น Ns

การที่คณะนักวิทยาศาสตร์ต่างคณะตั้งชื่อแตกต่างกัน ทำให้เกิดความสับสน International Union of Pure and Applied Chemistry (IUPAC) จึงได้กำหนดระบบการตั้งชื่อขึ้นใหม่ โดยใช้กับชื่อธาตุที่มีเลขอะตอมเกิน 100 ขึ้นไป ทั้งนี้ให้ตั้งชื่อธาตุโดยระบุเลขอะตอมเป็นภาษาละติน แล้วลงท้ายด้วย iumระบบการนับเลขในภาษาละตินเป็นดังนี้

0 = nil (นิล) 1 = un (อุน)

2 = bi (ไบ) 3 = tri (ไตร)

4 = quad (ควอด) 5 = pent (เพนท์)

6 = hex (เฮกซ์) 7 = sept (เซปท์)

8 = oct (ออกตฺ) 9 = enn (เอนน์)

เช่น - ธาตุที่ 104 ตามระบบ IUPAC อ่านว่า อุนนิลควอเดียม (Unnilquadium) สัญลักษณ์Unq

- ธาตุที่ 105 ตามระบบ IUPAC อ่านว่า อุนนิลเพนเทียม (Unnilpentium) สัญลักษณ์Unp

การจัดตารางธาตุเป็นหมู่เป็นคาบ ทำให้ศึกษาสมบัติต่าง ๆ ของธาตุได้ง่ายขึ้น สามารถทำนายสมบัติบางประการของธาตุบางธาตุได้ กล่าวคือธาตุที่อยู่ในหมู่เดียวกันจะมีสมบัติต่าง ๆ คล้าย ๆ กัน และธาตุที่อยู่ในคาบเดียวกัน จะมีแนวโน้มของการเปลี่ยนแปลงสมบัติต่าง ๆ ต่อเนื่องกันไป ซึ่งจะกล่าวถึงรายละเอียดต่อไป

บทเรียนที่ 12 รัศมีอะตอม

1. รัศมีอะตอม

ขนาดอะตอมหาได้จากเทคนิคทาง x-ray diffraction และ microwave spectroscopy

ถ้าอะตอมเรียงตัวอย่างมีระเบียบแบบชิดกันมากที่สุด ขนาดของอะตอมจะหาได้จากความสัมพันธ์ ดังนี้

ขนาดของ 1 อะตอม =

ปริมาตรของ 1 โมล =

จากแบบจำลองอะตอมแบบกลุ่มหมอก อะตอมมีขอบเขตที่ไม่แน่นอน ระยะระหว่างนิวเคลียสถึงผิวอะตอมมีค่าไม่คงที่ ทำให้หาขนาดของอะตอมที่แท้จริงไม่ได้ จากแบบจำลองของอะตอมตามทฤษฎีของโบร์ อิเล็กตรอนในไฮโดรเจนอะตอมอาจมีพลังงานได้หลายค่า ขนาดอะตอมของไฮโดรเจนจึงขึ้นอยู่กับว่าอิเล็กตรอนอยู่ในระดับพลังงานใด ถ้าอยู่ในระดับพลังงานสูง จะอยู่ห่างจากนิวเคลียสมาก ขนาดอะตอมจะใหญ่ และถ้าอยู่ในระดับพลังงานต่ำ จะอยู่ใกล้นิวเคลียส ขนาดอะตอมจะเล็ก ดังนั้นจึงทำให้หาขนาดของอะตอมที่แท้จริงไม่ได้

ในทางปฏิบัตินิยมบอกขนาดอะตอมด้วยรัศมีอะตอม โดยพิจารณาจากเส้นผ่านศูนย์กลางของโมเลกุลอะตอมคู่ หรือ อะตอม 2 อะตอมที่อยู่ชิดกัน โดยแบ่งรัศมีอะตอมเป็น 3 ประเภท

ก. รัศมีโลหะ (metallic radii)เนื่องจากโลหะมีการจัดเรียงอะตอมแบบชิดกัน รัศมีอะตอมโลหะจึงหาได้จากความยาวพันธะโลหะหารด้วย 2 หรือระยะระหว่างนิวเคลียสของโลหะ 2 อะตอมหารด้วย 2

ข. รัศมีโคเวเลนต์ (covalent radii)ได้จากความยาวของพันธะโคเวเลนต์หารด้วย 2 หรือ ระยะระหว่างนิวเคลียสของอะตอม 2 อะตอมที่ยึดเหนี่ยวกันด้วยพันธะโคเวเลนต์หารด้วย 2

เช่น ความยาวพันธะของ Cl - Cl = 198 พิโคเมตร (pm)

เพราะฉะนั้นรัศมีโคเวเลนต์ของ Cl = 198/2 = 99 พิโคเมตร

ค. รัศมีวันเดอร์วาลส์ (van der wall radii)ได้จากความยาวระหว่างนิวเคลียสของอโลหะ 2 อะตอม ที่ไม่เกิดพันธะกันหารด้วย 2 เช่น รัศมีวันเดอร์วาลส์ของ Cl = 155 พิโกเมตร

จะเห็นได้ว่าโลหะมีรัศมีอะตอมชนิดเดียวคือ รัศมีโลหะ แต่อโลหะมีรัศมีอะตอม 2 ชนิดคือ รัศมีโคเวเลนต์และรัศมีวันเดอร์วาลส์ ซึ่งในอะตอมชนิดเดียวกันรัศมีวันเดอร์วาลส์จะยาวกว่ารัศมีโคเวเลนต์

ตารางที่12เปรียบเทียบความยาวของรัศมีอะตอมระหว่างรัศมีโคเวเลนต์และรัศมีวันเดอร์วาลส์ของโลหะบางชนิด

ดังนั้นการกล่าวถึงรัศมีอะตอมจึงควรอ้างถึงด้วยว่าเป็นรัศมีอะตอมชนิดใด และการเปรียบเทียบขนาดอะตอมจะต้องใช้รัศมีอะตอมประเภทเดียวกันด้วย อย่างไรก็ตามการบอกค่ารัศมีอะตอมโดยทั่วไป จะหมายถึง รัศมีโคเวเลนต์ซึ่งรัศมีโคเวเลนต์สามารถหาได้จาก ความยาวของพันธะโคเวเลนต์ดังกล่าวมาแล้ว และถ้าตั้งสมมติฐานว่ารัศมีของอะตอมหนึ่งๆ ในโมเลกุลใดๆ มีค่าเท่ากัน จะสามารถหารัศมีอะตอมของธาตุต่างๆ ได้ เช่น

ก. ในโมเลกุลไฮโดรเจน

ความยาวพันธะของ H - H = 72 pm

เพราะฉะนั้นรัศมีอะตอมของ H = 74/2 = 37 pm

ข. ในโมเลกุล HCl

ความยาวพันธะของ H-Cl = 136 pm

รัศมีอะตอมของ H = 37 pm (จาก ข้อ ก.)

เพราะฉะนั้นรัศมีอะตอมของ Cl = 137 - 37 = 99 pm

ค. ในโมเลกุล CCl4

ความยาวพันธะของ C-Cl = 176 pm

รัศมีอะตอมของ Cl = 99 pm (จาก ข้อ ข.)

เพราะฉะนั้นรัศมีอะตอมของ C = 176 - 99 = 77 pm

ความสัมพันธ์ระหว่างขนาดอะตอมกับตารางธาตุ

พิจารณารัศมีอะตอมของธาตุต่างๆ ในตารางธาตุดังต่อไปนี้

บทเรียนที่ 13 พลังงานไอออไนเซชัน

พลังงานไอออไนเซชัน (Ionization Energy)

พลังงานไอออไนเซชันหมายถึง พลังงานที่ต้องการใช้สำหรับทำให้อิเล็กตรอนวงนอกสุดของอะตอมหรือไอออนในสภาวะก๊าซ หลุดออกไป 1 อิเล็กตรอน

เขียนเป็นสมการทั่วๆ ไปได้ดังนี้

X (g) + IE ------> X+(g) + e-

IE คือ พลังงานไอออไนเซชัน

หมายเหตุ

1.พลังงานไอออไนเซชัน จะต้องเกี่ยวข้องกับอิเล็กตรอนครั้งละ 1 อิเล็กตรอนเท่านั้น มิฉะนั้นจะไม่ใช่พลังงาน ไอออไนเซชัน

เช่น X (g) --------> X2+(g) + 2e-

X+(g) ---------> X3+(g) + 2e-

ทั้งสองปฏิกิริยาไม่ใช่พลังงานไอออไนเซชัน

2. พลังงานไอออไนเซชัน จะต้องเกี่ยวข้องกับอะตอมหรือไอออนที่อยู่ในสภาวะก๊าซเท่านั้น เช่น

X (g) + IE1ฎ X+(g) + e-

X+(g) + IE2ฎ X2+(g) + e-

ทั้ง IE1และ IE2ต่างก็เป็นพลังงานไอออไนเซชัน

พลังงานที่ใช้ในปฏิกิริยาต่อไปนี้ ไม่ใช่พลังงานไอออไนเซชัน

X (s) -------> X+(g) + e-

X (l) --------> X+(g) + e-

X (g) --------> X+(aq) + e-

ฯลฯ

3. เมื่อดึงอิเล็กตรอนตัวที่ 1, 2, 3 …… ออก จะเรียกชื่อว่า เป็นพลังงานไอออไนเซชันลำดับที่ 1, 2, 3 , .. ตามลำดับ เขียนย่อๆ เป็น IE1, IE2, IE3, ….

เขียนสมการแสดงค่า IE1, IE2, IE3, …. ได้ดังนี้

X (g) + IE1------> X+(g) + e-

X+(g) + IE2------> X2+(g) + e-

X2+(g) + IE3-------> X3+(g) + e-

โดยที่ในธาตุแต่ละชนิด IE1< IE2< IE3

พลังงานไอออไนเซชันลำดับที่1 ( IE1)

พลังงานไอออไนเซชันลำดับที่ 1 ( IE1)คือ พลังงานไอออไนเซชันที่ใช้สำหรับดึงอิเล็กตรอนตัวแรกออกจากอะตอมที่เป็นก๊าซ เขียนเป็นสมการทั่ว ๆ ไปได้ดังนี้

M(g) ---------> M+(g) + e-; IE1

เช่น Be(g) ---------> Be+(g) + e-; IE1= 0.906 MJ/mol

หมายความว่า ถ้าต้องการดึงอิเล็กตรอนตัวที่อยู่วงนอกสุดของอะตอม Be ที่เป็นก๊าซ จะต้องใช้พลังงานอย่างน้อย 0. 906 MJ/mol

ตัวอย่างอื่น ๆ เช่น

Cl(g) ----------> Cl+(g) + e-; IE1= 1.257 MJ/mol

Ne(g) ----------> Ne+(g) + e-; IE1= 2.087 MJ/mol

พลังงานไอออไนเซชันลำดับที่2 ( IE2)

พลังงานไอออไนเซชันลำดับที่ 2 ( IE2) คือ พลังงานไอออไนเซชันที่ใช้สำหรับดึงอิเล็กตรอนตัวที่สองออกจากไอออนบวกที่เป็นก๊าซ เขียนเป็นสมการทั่ว ๆ ไปได้ดังนี้

M+(g) --------> M2+(g) + e-; IE2

เช่น

N+(g) ---------> N2+(g) + e-; IE2= 2.862 MJ/mol

Al+(g) ---------> Al2+(g) + e-; IE2= 1.823 MJ/mol

พลังงานไอออไนเซชันลำดับอื่น ๆ ก็พิจารณาได้ในทำนองเดียวกัน เขียนเป็นสมการทั่ว ๆ ไปได้ดังนี้ คือ

M(n)+(g) ---------> M(n+1)+(g) + e-; IEn+1

ธาตุไฮโดรเจนมี 1 e จึงมีเพียง IE1ค่าเดียว ธาตุอื่น ๆ มีหลายอิเล็กตรอนก็จะมี IE หลายค่า ถ้าอะตอมของธาตุหนึ่งมี n อิเล็กตรอน จะมีพลังงานไอออไนเซชันได้ถึง n ลำดับ เช่น

ธาตุ He มี 2 อิเล็กตรอน จะมีพลังงานไอออไนเซชัน 2 ลำดับ

ธาตุ Cl มี 17 อิเล็กตรอน จะมีพลังงานไอออไนเซชัน 17 ลำดับ

ธาตุ Mg มี 12 อิเล็กตรอน จะมีพลังงานไอออไนเซชัน 12 ลำดับ เป็นต้น

ในกรณีที่ธาตุนั้นเป็นของแข็งหรือของเหลว ในตอนแรกที่ใส่พลังงานเข้าไปจะไม่ไปใช้อิเล็กตรอน แต่จะใช้ในการเปลี่ยนสถานะ ดังนั้นไม่ว่าธาตุจะอยู่ในสถานะใด เมื่อได้รับพลังงานมากพอก็จะเปลี่ยนภาวะมาเป็นอะตอมในสถานะก๊าซ และถ้าให้พลังงานต่อไปอีกจนทำให้อิเล็กตรอนหลุดออกจากอะตอมที่เป็นก๊าซ พลังงานส่วนนี้จะเรียกว่าพลังงานไอออไนเซชัน

ดังนั้น พลังงานที่ใช้ในการเปลี่ยนแปลงต่อไปนี้จึงไม่ใช่พลังงานไอออไนเซชัน

M (s) --------> M2+(g) + e-

M (l) ---------> M+(g) + e-

M+(g) ---------> M3+(g) + e-

M+(s) ----------> M+(aq) + e-

M (l) ----------> M+(aq) + e-

ฯลฯ

ปัจจัยที่มีผลต่อค่าพลังงานไอออไนเซชัน

ก.ขนาดอะตอมถ้าอะตอมมีขนาดเล็ก จะมีค่า IE มาก แต่ถ้าอะตอมมีขนาดใหญ่จะมีค่า IEจะน้อย

ข. ประจุในนิวเคลียสถ้าอะตอมมีประจุในนิวเคลียสมาก ค่า IE จะมาก แต่ถ้ามีประจุในนิวเคลียสน้อย ค่า IE จะน้อย โดยทั่วๆ ไปขนาดของอะตอมจะมีผลต่อค่า IE มากกว่าประจุในนิวเคลียส นอกจากนี้ การพิจารณาค่า IE ของธาตุต่างๆ อาจจำเป็นต้องพิจารณาปัจจัยอื่นๆ นอกเหนือจากนี้ด้วย เช่น

-โครงสร้างอะตอม กล่าวคือ อะตอมหรือไอออนที่มีการจัดเรียงอิเล็กตรอนครบออกเตต เช่น Na+(g) , Mg2+(g), F-(g), Ne ซึ่งอยู่ในภาวะที่เสถียร จะมีค่า IE สูงมาก

-แรงผลักของอิเล็กตรอนใน orbital เดียวกัน ซึ่งทำให้เกิดแรงผลักระหว่างอิเล็กตรอนทำให้ค่า IE น้อยลง

ความสัมพันธ์ระหว่างIE1กับตารางธาตุพิจารณาค่า IE1ของธาตุต่างๆ จากกราฟต่อไปนี้

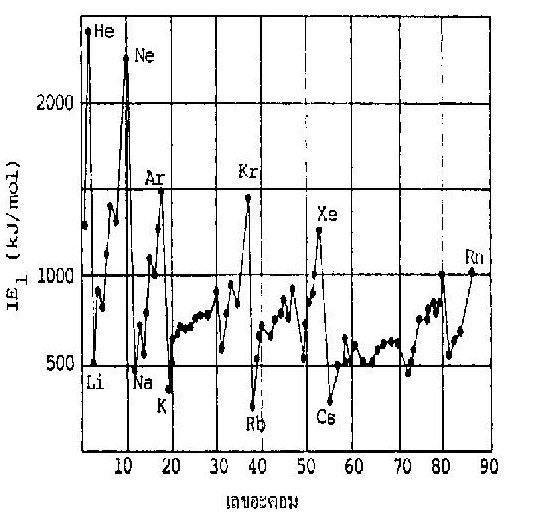
จากกราฟจะเห็นได้ว่าค่า IE1ในหมู่และในคาบเดียวกันมีแนวโน้มของการเปลี่ยนแปลงที่สำคัญพอจะสรุปได้ดังนี้

ก. ธาตุในหมู่เดียวกันค่า IE1จะลดลงเมื่อเลขอะตอมเพิ่มขึ้น ทั้งนี้เพาะธาตุในหมู่เดียวกัน เมื่อเลขอะตอมเพิ่มขึ้นขนาดของอะตอมจะใหญ่ขึ้น ทำให้แรงยึดเหนี่ยวระหว่างนิวเคลียสกับอิเล็กตรอนน้อยลง ค่าจึงลดลง (ดูค่า IE1ของธาตุหมู่IA ในตารางที่ 21)

ข. ธาตุในคาบเดียวกันค่า IE1จะเพิ่มขึ้นเมื่อเลขอะตอมเพิ่มขึ้น ทั้งนี้เพราะขนาดอะตอมเล็กลงตามลำดับนั่นเอง ดังนั้นโลหะจึงมีค่า IE1ต่ำกว่าอโลหะ (ดูค่า IE1ของธาตุในคาบที่ 2 ในตารางที่ 22)

ตารางที่21แสดงค่า IE1ของธาตุในหมู่เดียวกัน (หมู่ IA)

ตารางที่22แสดงค่า IE1ของธาตุในคาบเดียวกัน (คาบที่ 2)

จะเห็นได้ว่าธาตุในหมู่เดียวกันเมื่อเลขอะตอมเพิ่มขึ้น ค่า IE1ลดลงตามลำดับ แต่ธาตุในคาบเดียวกัน เมื่อเลขอะตอมเพิ่มขึ้น ค่า IE1ส่วนใหญ่เพิ่มขึ้น แต่มีบางธาตุค่า IE1ลดลงอย่างไรก็ตามเมื่อพิจารณาโดยรวม จากการดูแนวโน้มของการเปลี่ยนแปลงในกราฟรูปที่ 3.12 ก็จะพบว่าในคาบเดียวกันเมื่อเลขอะตอมเพิ่มขึ้นค่า IE1มีแนวโน้มเพิ่มขึ้น การที่ค่า IE1ของบางธาตุไม่เพิ่มขึ้น อาจจะอธิบายได้ดังนี้

1. ในคาบที่ 2 ค่า IE1ของ Be มากกว่า B ทั้งๆ ที่ Be มีขนาดใหญ่กว่า B เนื่องจากปัจจัยเกี่ยวกับโครงสร้างของอะตอม

4Be = 1s22s2มีเวเลนต์อิเล็กตรอนเป็น 2s2ซึ่งมีลักษณะคล้ายกับ He ดังนั้นโครงสร้างอะตอมจึงเสถียรมาก ค่า IE1จึงสูง

5B = 1s22s22p1มีเวเลนต์อิเล็กตรอนเป็น 2p1ซึ่งไม่ครบออกเตต ทำให้โครงสร้างอะตอมไม่เสถียรเท่า Be ดังนั้น IE1จึงน้อยกว่าของ Be

2. ในกรณีของ N และ O ปรากฏว่า N มี IE1สูงกว่า O เพราะปัจจัยเกี่ยวกับแรงผลักของอิเล็กตรอนในออร์บิทอล (orbital) เดียวกัน

7N = 1s22s22p3

อิเล็กตรอนทั้ง 3 ใน p - obital กระจายกันอยู่ แรงผลักระหว่างอิเล็กตรอนกับอิเล็กตรอนค่อนข้างน้อย อะตอมอยู่ในภาวะเสถียร

8O = 1s22s22p4

อิเล็กตรอนทั้ง 4 ใน p- orbital กระจายกันอยู่ แต่มีอยู่ 1 orbital ที่มี 2 อิเล็กตรอนจึงมีแรงผลักระหว่างอิเล็กตรอนเกิดขึ้น ดังนั้นอะตอมจึงเสถียรน้อยกว่า N ทำให้ค่า IE1น้อยกว่

บทเรียนที่ 14 อิเล็กโทรเนกาติวิตี

อิเล็กโทรเนกาติวิตี เป็นความสามารถของอะตอมของธาตุในการดึงดูดอิเล็กตรอนคู่ร่วมพันธะให้เข้าใกล้นิวเคลียส ธาตุที่มีอิเล็กโทรเนกาติวิตีสูงกว่าจะแสดงอำนาจไฟฟ้าลบ ส่วนธาตุที่มีอิเล็กโทรเนกาติวิตีต่ำกว่า จะแสดงอำนาจไฟฟ้าบวก

ปัจจัยที่มีผลต่อค่าอิเล็กโทรเกาติวิตีเหมือนกับปัจจัยที่มีผลต่อค่า IE คือ

ก. ขนาดของอะตอมอะตอมที่มีขนาดเล็ก จะมีค่าอิเล็กโทรเนกาติวิตีสูงกว่าอะตอมที่มีขนาดใหญ่ เนื่องจากอะตอมที่มีขนาดเล็ดสามารถดึงดูดอิเล็กตรอนคู่ร่วมพันธะให้เเข้าใกล้นิวเคลียสได้มากกว่า

ข. ประจุในนิวเคลียสอะตอมที่มีประจุในนิวเคลียสมากกว่า จะมีค่าอิเล็กโทรเนกาติวิตีสูงกว่า เพราะสามารถดึงอิเล็กตรอนคู่ร่วมพันธะให้เข้าใกล้นิวเคลียสได้มากกว่า

ดังนั้น ธาตุที่มีขนาดเล็กและมีประจุในนิวเคลียสมาก จะมีค่าอิเล็กโทรเนกาติวิตีสูง

อย่างไรก็ตาม โดยทั่วๆ ไปขนาดของอะตอมจะมีผลต่อค่าอิเล็กโทรเนกาติวิตีมากกว่าประจุในนิวเคลียส เช่น

Na มีรัศมีอะตอม 186 pm มีอิเล็กโทรเนกาติวิตี 0.9

Mg มีรัศมีอะตอม 160 pm มีอิเล็กโทรเนกาติวิตี 1.2

Mg มีขนาดเล็กกว่าและมีประจุในนิวเคลียสมากกว่า จึงมีอิเล็กโทรเนกาติวิตีมากกว่า

อีกตัวอย่างหนึ่ง

Mg มีรัศมีอะตอม 160 pm มีอิเล็กโทรเนกาติวิตี 1.2

Ca มีรัศมีอะตอม 197 pm มีอิเล็กโทรเนกาติวิตี 1.0

Mg มีขนาดเล็กกว่า จึงมีอิเล็กโทรเนกาติวิตีมากกว่า Ca (ถึงแม้ว่า Mg จะมีประจุในนิวเคลียสน้อยกว่า Ca )

การคำนวณค่าอิเล็กโทรเนกาติวิตี

อิเลกโทรเนกาติวิตีของธาตุหนึ่งๆ ได้จากการคำนวณไม่ใช่ได้จากการทดลอง ซึ่งการคำนวณมีหลายวิธีต่างๆ กัน ไลนัส พอลิง (Linus Pauling) นักเคมีชาวอเมริกันได้คำนวณค่าอิเล็กโทรเนกาติวิตีของธาตุต่างๆ ที่สามารถเกิดพันธะระหว่างกันได้ โดนพิจารณาจากปัจจัยเกี่ยวกับพลังงานพันธะของพวกโมเลกุลอะตอมคู่ดังต่อไปนี้

ENA- ENB=

ENA= อิเล็กโทรเนกาติวิตีของธาตุ A

ENB= อิเล็กโทรเนกาติวิตีของธาตุ B

DHAB= พลังงานพันธะของ A - B

DHAA= พลังงานพันธะของ A - A

DHBB= พลังงานพันธะของ B - B

(หน่วยของพลังงานเป็น kcal/mol)

จากความสัมพันธ์ดังกล่าว เมื่อทราบพลังงานพันธะจะสามารถคำนวณอิเล็กโทรเนกาติวิตีเปรียบเทียบระหว่างธาตุ 2 ธาตุที่เกิดพันธะกันได้ ซึ่งถ้าทราบค่าอิเล็กโทรเนกาติวิตีของธาตุหนึ่ง จะหาค่าอิเล็กโทรเนกาติวิตีของอีกธาตุหนึ่งได้

พอลิงใช้วิธีเปรียบเทียบโดยกำหนดให้ธาตุ F ซึ่งมีขนาดเล็กที่สุดและเกิดพันธะได้ มีอิเล็กโทรเนกาติวิตีสูงที่สุดคือ เท่ากับ 4.0 หลังจากนั้นจึงคำนวณอิเล็กโทรเนกาติวิตีของธาตุอื่นๆ โดยการเปรียบเทียบกับธาตุ F และธาตุอื่นๆ ที่ทาบค่าอิเล็กโทรเนกาติวิตีแล้ว

ความสัมพันธ์ระหว่างอิเล็กโทรเนกาติวิตีกับตารางธาตุ

พิจารณาค่าอิเล็กโทรเนกาติวิตีของธาตุต่างๆ ในตารางธาตุดังต่อไปนี้

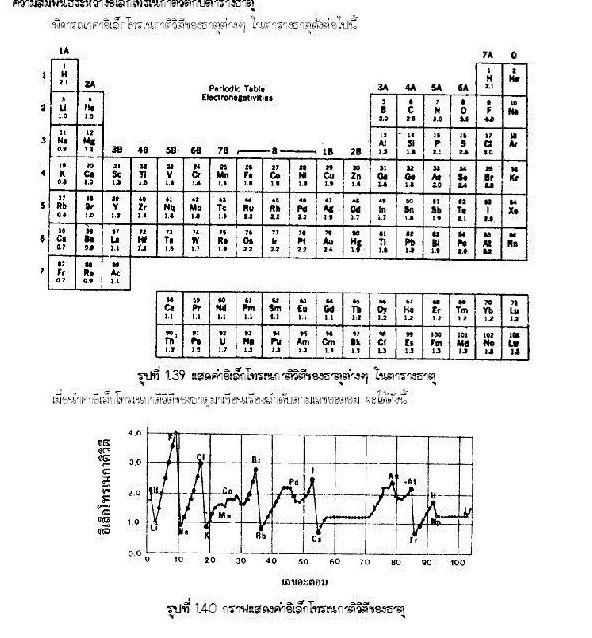
จากลักษณะของกราฟจะสามารถสรุปแนวโน้มของการเปลี่ยนแปลงค่าอิเล็กโทรเนกาติวิตีของธาตุในหมู่และในคาบเดียวกันได้ดังนี้

ก. ธาตุในหมู่เดียวกันค่าอิเล็กโทรเนกาติวิตีมีแนวโน้มลดลงเมื่อเลขอะตอมเพิ่มขึ้น เนื่องจากขนาดอะตอมใหญ่ขึ้น ทำให้แรงดึงดูดระหว่างนิวเคลียสกับอิเล็กตรอนมีค่าลดลง ค่าอิเล็กโทรเนกาติวิตีจึงต่ำ

ข. ธาตุในคาบเดียวกันค่าอิเล็กโทรเนกาติวิตีมีแนวโน้มเพิ่มขึ้น เมื่อเลขอะตอมเพิ่มขึ้น เนื่องจากขนาดอะตอมเล็กลง ทำให้แรงดึงดูดระหว่างนิวเคลียสกับอิเล็กตรอนมีค่ามากขึ้น สามารถดึงดูดอิเล็กตรอนคู่ร่วมพันธะให้เข้าใกล้นิวเคลียส ค่าอิเล็กโทรเนกาติวิตีจึงสูง

ค. ธาตุเฉื่อยไม่มีค่าอิเล็กโทรเนกาติวิตี เนื่องจากธาตุเฉื่อยเกิดสารประกอบได้ยาก จึงไม่ได้คำนวณไว้

จากค่าอิเล็กโทรเนกาติวิตีของธาตุต่างๆ ในตารางธาตุจะเห็นได้ว่าโลหะซึ่งอยู่ทางซ้ายมือของตารางธาตุ มีค่าอิเล็กโทรเนกาติวิตีต่ำ เมื่อมีการสร้างพันธะกับอะตอมของธาตุอื่น อิเล็กตรอนจึงมีแนวโน้มที่จะถูกดึงออกจากอะตอมได้ง่าย ธาตุเหล่านี้จัดว่าเป็นพวกชอบให้อิเล็กตรอนหรือเรียกว่า electropositive element ในขณะที่อโลหะ (ยกเว้นธาตุเฉื่อย) ซึ่งอยู่ทางขวามือของตารางธาตุ มีค่าอิเล็กโทรเนกาติวิตีสูง เมื่อมีการสร้างพันธะกับอะตอมของธาตุที่มีอิเล็กโทรเนกาติวีตีต่ำกว่า จะสามารถดึงอิเล็กตรอนคู่ร่วมพันธะให้เข้าหาตัวได้ง่าย ธาตุเหล่านี้จัดว่าเป็นพวกชอบอิเล็กตรอนหรือเรียกว่า electronegative element

ประโยชน์ของอิเล็กโทรเนกาติวิตี

1.ใช้ทำนายว่าธาตุ 2 ธาตุ เมื่อเกิดสารประกอบจะเป็นไอออนิกหรือโคเวลนต์ โดยพิจารณาจากผลต่างของค่าอิเล็กโทรเนกาติวิตีระหว่างธาตุคู่ร่วมพันธะ แล้วคำนวณออกมาเป็น% ionic ดังนี้

ตารางที่23 แสดงเปอร์เซนต์ไอออนิก จากผลต่างของค่าอิเล็กโทรเนกาติวิตี

(EN) = ผลต่างของค่าอิเล็กโทรเนกาติวิตีของธาตุคู่ร่วมพันธะ

โดยทั่วไปสารประกอบธาตุคู่ที่มี %ionic มากกว่า 50 % จะจัดว่าเป็นสารไอออนิก ยิ่งมี %ionic มากเท่าใด ก็จะยิ่งแสดงสมบัติของความเป็นไอออนิกมากขึ้นเท่านั้น เช่น

(EN) ของ Cl - Cl = 0 มี %ionic = 0 แสดงว่าเป็นสารโคเวเลนต์

(EN) ของ NaCl = 2.1 มี %ionic = 67 % แสดงว่าเป็นสารไอออนิก

(EN) ของ KCl = 2.2 มี %ionic = 70 % แสดงว่าเป็นสารไอออนิก

(EN) ของ LiCl = 2.0 มี %ionic = 63 % แสดงว่าเป็นสารไอออนิก

แสดงว่า NaCl , NaCl และ LiCl ต่างก็เป็นสารไอออนิก โดยมีความเป็นไอออนิกเรียงลำดับดังนี้ KCl > NaCl > LiCl

2. การพิจารณาสภาพขั้วของพันธะ โดยเฉพาะโมเลกุลโคเวเลนต์ เมื่อต้องการจะทราบว่าพันธะมีขั้วหรือไม่ พันธะใดมีขั้วของพันธะมากกว่ากัน ให้ดูจากผลต่างของค่าอิเล็กโทรเนกาติวิตี ถ้ามีค่าอิเล็กโทรเนกาติวิตีเท่ากันจะได้ว่าพันธะไม่มีขั้ว เช่น H-H, NN แต่ถ้ามีค่าอิเล็กโทรเนกาติวิตีต่างกันจะได้พันธะที่มีขั้ว ยิ่งต่างกันมากก็จะยิ่งมีขั้วมาก ซึ่งถ้าต่างกันมากกว่า 2 จะถือว่าเป็นพันธะไอออนิกดังที่ได้กล่าวมาแล้ว เช่น

(EN) ของ Cl - Cl = 0

(EN) ของ H - Cl = 0.9

(EN) ของ H - Br = 0.7

(EN) ของ H - I = 0.4

แสดงว่า Cl-Cl เป็นพันธะไม่มีขั้ว HCl, HBr, และ HI เป็นพันธะมีขั้ว โดยเรียงลำดับขั้ว ของพันธะจากมากไปน้อยได้ดังนี้

HCl > HBr > HI

3. ใช้ประกอบการเขียนสูตรสารประกอบ โดยทั่วๆ ไปในการเขียนสูตรของสารประกอบของธาตุที่มีค่าอิเล็กโทรเนกาติวิตีต่ำจะเขียนไว้ข้างหน้าและธาตุที่มีอิเล็กโทรเนกาติวิตีสูงกว่าจะเขียนไว้ข้างหลัง เช่น NaCl, Cl2O, OF2เป็นต้น

นอกจากสมบัติของธาตุในตารางธาตุเกี่ยวกับขนาดอะตอม พลังงานไอออไนเซชัน จุดหลอมเหลว จุดเดือดและค่าอิเล็กโทรเนกาติวิตีแล้วยังมีสมบัติอื่นๆ ของธาตุที่น่าสนใจอีกเช่น อิเล็กตรอนอัฟฟินิตี และความเป็นโลหะของธาตุ เป็นต้น