ตัวประกอบและการหาตัวประกอบ
ตัวประกอบและการหาตัวประกอบ
- จำนวนนับ คือ จำนวนเต็มบวก ได้แก่ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …
- การหารลงตัว คือ การหารที่ไม่มีเศษ หรือเศษเป็น “0”
- ตัวประกอบของจำนวนนับใด ๆ คือ จำนวนนับที่นำไปหารจำนวนนับนั้นได้ลงตัว
- จำนวนเฉพาะ คือ จำนวนนับที่มีตัวประกอบเพียงสองตัว คือ 1 กับจำนวนนับนั้น
- ตัวประกอบเฉพาะ คือ ตัวประกอบที่เป็นจำนวนเฉพาะ
- การแยกตัวประกอบของจำนวนใด ๆ คือ การเขียนจำนวนนั้นในรูป ผลคูณของตัวประกอบเฉพาะ (อาจจะมีตัวประกอบมากกว่า 2 จำนวน)
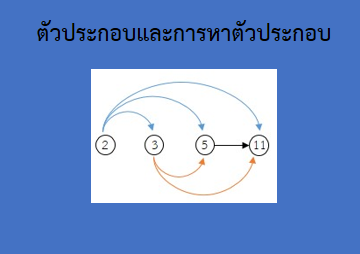
ภาพที่ 1 ตัวประกอบและการหาตัวประกอบ
ที่มา : ปิยวดี เอ่งฉ้วน
การหาตัวประกอบ
การเขียนจำนวนในรูปผลคูณของตัวประกอบเฉพาะ และจำนวนเฉพาะหลัก คือ 2, 3, 5, 7, 11, 13, 17, และ 19 (จำนวนเฉพาะที่ต้องจำ)
ตัวอย่าง
- จงหาตัวประกอบของ 24
วิธีทำ
วิธีที่ 1 (DMFT การหาร)
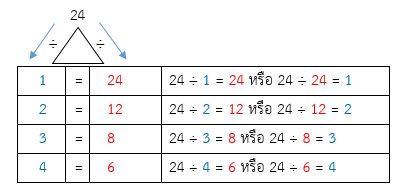
ดังนั้น จำนวนตัวประกอบของ 24 มีทั้งหมด 8 จำนวน คือ 1, 2, 3, 4, 6, 8, 12, 24
การหาจำนวนตัวประกอบทั้งหมด
การหาจำนวนตัวประกอบทั้งหมด คือ จำนวนนับที่นำไปหารจำนวนนับนั้นได้ลงตัวทั้งหมด
(ให้จำนวนเฉพาะหลัก คือ 2, 3, 5, 7, 11, 13, 17, และ 19)
ตัวอย่าง
- จงหาตัวประกอบของ 24
วิธีทำ การแยกตัวประกอบของ 24 จะได้ ดังนี้
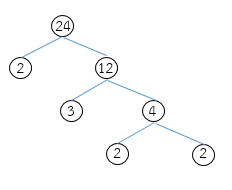
จากการแยกตัวประกอบของ 24 จะได้ 2 × 2 × 2 × 3
= (2 × 2 × 2) × 3
= 8 × 3
= 24
ดังนั้น แสดงว่าการแยกตัวประกอบของ 24 เป็นจริง
วิธีการหาตัวประกอบทั้งหมดของ 24 มีกี่จำนวน อะไรบ้าง
จากการแยกตัวประกอบของ 24 จะได้เท่ากับ 8 × 3
ตัวประกอบของ 8 มี 4 จำนวน คือ 1, 2, 4, 8
ตัวประกอบของ 3 มี 2 จำนวน คือ 1, 3
ดังนั้น ตัวประกอบทั้งหมดของ 24 คือ 4 × 2 = 8 จำนวน คือ 1, 2, 3, 4, 6, 8, 12, 24
- การหาตัวประกอบทั้งหมดของ 24 ด้วยวิธีการแยกตัวประกอบ
วิธีทำ จากการแยกตัวประกอบของ 24 จะได้ 2 × 2 × 2 × 3
เมื่อ
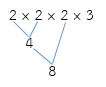
นำจำนวน 2, 4, 8 มาคูณกับ 3 ดังนี้
2 × 3 = 6
4 × 3 = 12
8 × 3 = 24
(1 เป็นตัวประกอบของจำนวนนับทุกจำนวน)
ดังนั้น ตัวประกอบทั้งหมดของ 24 คือ 1, 2, 3, 4, 6, 8, 12, 24
ตอบ ตัวประกอบทั้งหมดของ 24 มี 8 จำนวน คือ 1, 2, 3, 4, 6, 8, 12, 24
- จงหาตัวประกอบของ 72
วิธีทำ แยกตัวประกอบของ 72 ดังนี้
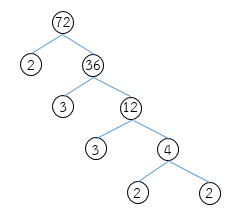
จากการแยกตัวประกอบของ 72 จะได้ 2 × 2 × 2 × 3 × 3
= (2 × 2 × 2) × (3 × 3)
= 8 × 9
= 72
ดังนั้น แสดงว่าการแยกตัวประกอบของ 72 เป็นจริง
วิธีการหาตัวประกอบทั้งหมดของ 72 มีกี่จำนวน อะไรบ้าง
จากการแยกตัวประกอบของ 72 จะได้เท่ากับ 8 × 9
ตัวประกอบของ 8 มี 4 จำนวน คือ 1, 2, 4, 8
ตัวประกอบของ 9 มี 3 จำนวน คือ 1, 3, 9
ดังนั้น ตัวประกอบทั้งหมดของ 72 คือ 4 × 3 = 12 จำนวน
เมื่อ
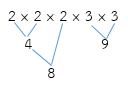
นำจำนวน 2, 4, 8 มาคูณกับ 3, 9 ดังนี้
(2, 4, 8) × 3
2 × 3 = 6
4 × 3 = 12
8 × 3 = 24
(2, 4, 8) × 9
2 × 9 = 18
4 × 9 = 36
8 × 9 = 72
(1 เป็นตัวประกอบของจำนวนนับทุกจำนวน)
ดังนั้น ตัวประกอบทั้งหมดของ 72 คือ 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
ตอบ ตัวประกอบทั้งหมดของ 72 มี 12 จำนวน คือ 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
ตรวจคำตอบ (DMFT การหาร)
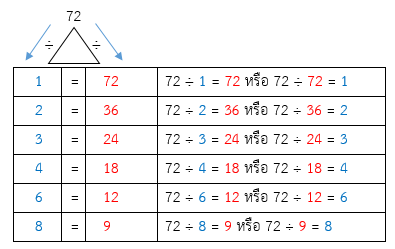
ดังนั้น ตัวประกอบของ 72 คือ 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72 เป็นจริง
- จงหาตัวประกอบของ 110
วิธีทำ แยกตัวประกอบของ 110 ดังนี้
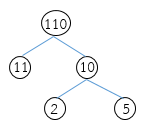
จากการแยกตัวประกอบของ 110 จะได้ 2 × 5 × 11
= (2 × 5) × 11
= 10 × 11
= 110
ดังนั้น แสดงว่าการแยกตัวประกอบของ 110 เป็นจริง
วิธีการหาตัวประกอบทั้งหมดของ 110 มีกี่จำนวน อะไรบ้าง
จากการแยกตัวประกอบของ 110 จะได้เท่ากับ 2 × 5 × 11
ตัวประกอบของ 2 มี 2 จำนวน คือ 1, 2
ตัวประกอบของ 5 มี 2 จำนวน คือ 1, 5
ตัวประกอบของ 11 มี 2 จำนวน คือ 1, 11
ดังนั้น ตัวประกอบทั้งหมดของ 110 คือ 2 × 2 × 2 = 8 จำนวน
เมื่อ 2 × 5 × 11
นำจำนวน
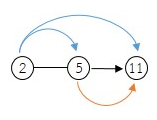
2 × 5 = 10
2 × 11 = 22
5 × 11 = 55
2 × 5 × 11 = 110
(1 เป็นตัวประกอบของจำนวนนับทุกจำนวน)
ดังนั้น ตัวประกอบทั้งหมดของ 110 คือ 1, 2, 5, 10, 11, 22, 55, 110
ตอบ ตัวประกอบทั้งหมดของ 110 มี 8 จำนวน คือ 1, 2, 5, 10, 11, 22, 55, 110
ตรวจคำตอบ
(DMFT การหาร)
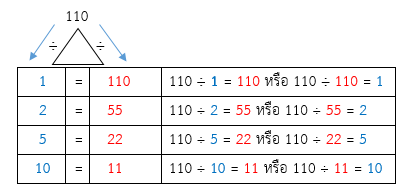
ดังนั้น ตัวประกอบของ 110 คือ 1, 2, 5, 10, 11, 22, 55, 110 เป็นจริง
- จงหาตัวประกอบของ 330
วิธีทำ แยกตัวประกอบของ 330 ดังนี้
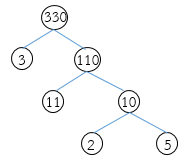
จากการแยกตัวประกอบของ 330 จะได้ 2 × 3 × 5 × 11
= (2 × 3) × (5 × 11)
= 6 × 55
= 330
ดังนั้น แสดงว่าการแยกตัวประกอบของ 330 เป็นจริง
วิธีการหาตัวประกอบทั้งหมดของ 330 มีกี่จำนวน อะไรบ้าง
จากการแยกตัวประกอบของ 330 จะได้เท่ากับ 2 × 3 × 5 × 11
ตัวประกอบของ 2 มี 2 จำนวน คือ 1, 2
ตัวประกอบของ 3 มี 2 จำนวน คือ 1, 3
ตัวประกอบของ 5 มี 2 จำนวน คือ 1, 5
ตัวประกอบของ 11 มี 2 จำนวน คือ 1, 11
ดังนั้น ตัวประกอบทั้งหมดของ 330 คือ 2 × 2 × 2 × 2 = 16 จำนวน
เมื่อ 2 × 3 × 5 × 11
ขั้นที่ 1
นำจำนวน
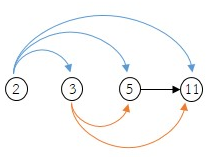
2 × 3 = 6
2 × 5 = 10
2 × 11 = 22
3 × 5 = 15
3 × 11 = 33
5 × 11 = 55
ขั้นที่ 2

2 × 3 × 5 = 30
2 × 3 × 11 = 66
2 × 5 × 11 = 110
3 × 5 × 11 = 165
2 × 3 × 5 × 11 = 330
(1 เป็นตัวประกอบของจำนวนนับทุกจำนวน)
ดังนั้น ตัวประกอบทั้งหมดของ 330 คือ 1, 2, 3, 5, 6, 10, 11, 15, 22, 30, 33, 55, 66, 110, 165, 330
ตอบ ตัวประกอบทั้งหมดของ 330 มี 16 จำนวน คือ 1, 2, 3, 5, 6, 10, 11, 15, 22, 30, 33, 55, 66, 110, 165, 330
ตรวจคำตอบ
(DMFT การหาร)
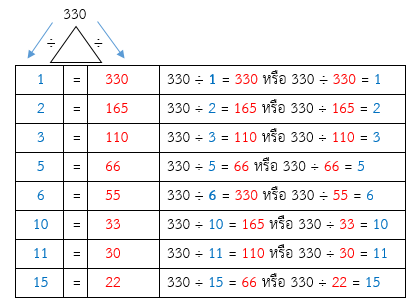
ดังนั้น ตัวประกอบของ 330 คือ 1, 2, 3, 5, 6, 10, 11, 15, 22, 30, 33, 55, 66, 110, 165, 330
เป็นจริง
- จงหาตัวประกอบของ 600
วิธีทำ แยกตัวประกอบของ 600 ดังนี้
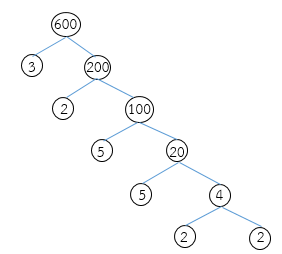
จากการแยกตัวประกอบของ 600 จะได้ 2 × 2 × 2 × 3 × 5 × 5
= (2 × 2 × 2) × 3 × (5 × 5)
= 8 × 3 × 25
= 600
ดังนั้น แสดงว่าการแยกตัวประกอบของ 600 เป็นจริง
วิธีการหาตัวประกอบทั้งหมดของ 600 มีกี่จำนวน อะไรบ้าง
จากการแยกตัวประกอบของ 600 จะได้เท่ากับ 8 × 3 × 25
ตัวประกอบของ 3 มี 2 จำนวน คือ 1, 3
ตัวประกอบของ 8 มี 4 จำนวน คือ 1, 2, 4, 8
ตัวประกอบของ 25 มี 3 จำนวน คือ 1, 5, 25
ดังนั้น ตัวประกอบทั้งหมดของ 600 คือ 2 × 4 × 3 = 24 จำนวน
เมื่อ
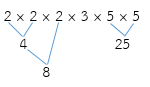
นำจำนวน (2, 4, 8) × 3 × (5, 25) ดังน
2 × 3 = 6
2 × 5 = 10
3 × 5 = 15
2 × 3 × 5 = 30
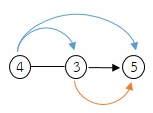
4 × 3 = 12
4 × 5 = 20
3 × 5 = 15
4 × 3 × 5 = 60
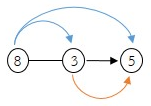
8 × 3 = 24
8 × 5 = 40
3 × 5 = 15
8 × 3 × 5 = 120
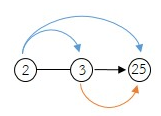
2 × 3 = 6
2 × 25 = 50
3 × 25 = 75
2 × 3 × 25 = 150
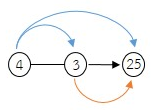
4 × 3 = 12
4 × 25 = 100
3 × 25 = 75
4 × 3 × 25 = 300
8 × 3 = 24
8 × 25 = 200
3 × 25 = 75
8 × 3 × 25 = 600
(1 เป็นตัวประกอบของจำนวนนับทุกจำนวน)
ดังนั้น ตัวประกอบทั้งหมดของ 600 คือ 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40, 50, 60, 75, 100, 120, 150, 200, 300, 600
ตอบ ตัวประกอบทั้งหมดของ 600 มี 24 จำนวน คือ 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40, 50, 60, 75, 100, 120, 150, 200, 300, 600
ตรวจคำตอบ
(DMFT การหาร)
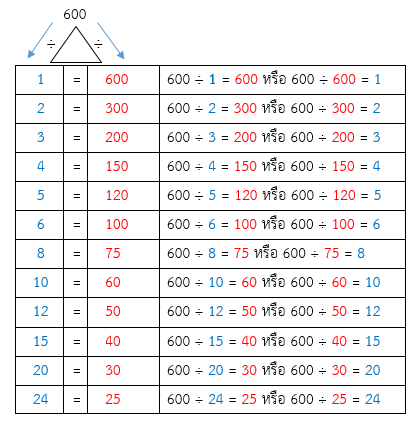
ดังนั้น ตัวประกอบของ 600 คือ 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40, 50, 60, 75, 100, 120, 150, 200, 300, 600 เป็นจริง
แหล่งที่มา
นิติกร ระดม. 2551. คู่มือครู อจท. คณิตศาสตร์ ป6. กรุงเทพมหานคร: อักษรเจริญทัศน์
กรมวิชาการ กระทรวงศึกษาธิการ. (2538). หนังสือเอกสารเสริมความรู้คณิตศาสตร์ ระดับประถมศึกษา อันดับที่3 (1). กรุงเทพมหานคร: โรงพิมพ์คุรุสภาลาดพร้าว.
ธิดาสิริ ภัทรากาญจน์. (2548). เกมคณิตปริศนา: พาสนุกปลูกปัญญา (3). กรุงเทพฯ: บริษัท ด่านสุทธาการพิมพ์ จำกัด
สำนักงานส่งเสริมการศึกษานอกระบบและการศึกษาตามอัธยาศัย. (2551). เอกสารสรุปเนื้อหาที่ต้องรู้รายวิชาคณิตศาสตร์ ระดับประถมศึกษา. กรุงเทพฯ:
สำนักงาน กศน.สำนักงานปลัดกระทรวงศึกษาธิการ.นางกนกวลี อุษณกรกุล. (2551). หนังสือเรียน รายวิชาพื้นฐาน คณิตศาสตร์ ม.1 เล่ม1 ชั้นมัธยมศึกษาปีที่ 1 (1). กรุงเทพมหานคร ; อักษรเจริญทัศน์
ทรงวิทย์ สุวรรณธาดา และคณะ. (2551). แบบฝึกหัด รายวิชาพื้นฐานกลุ่มสาระการเรียนรู้คณิตศาสตร์ คณิตศาสตร์ ป.6. กรุงเทพมหานคร: บริษัทแม็คเอ็ดยูเคชั่น จำกัด
กลับไปที่เนื้อหา
ตัวหารร่วม หรือ ตัวประกอบร่วม คือ จำนวนนับที่หารจำนวนตั้งแต่สองจำนวนขึ้นไปได้ลงตัว
ตัวหารร่วมมาก (ห.ร.ม.) คือ ตัวประกอบร่วมหรือตัวหารร่วมที่มากที่สุด
การหาตัวหารร่วมมาก (ห.ร.ม.) ของจำนวนนับตั้งแต่สองจำนวนขึ้นไปที่ต้องการ โดยการแยกตัวประกอบของจำนวนนับแต่ละจำนวน ซึ่ง ตัวหารร่วมมาก (ห.ร.ม.) หาได้จากผลคูณของจำนวนเฉพาะที่เป็นตัวประกอบร่วมของจำนวนเหล่านั้น
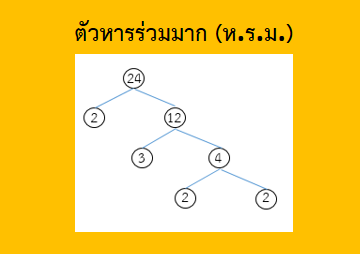
ภาพที่ 1 ตัวหารร่วมมาก (ห.ร.ม.)
ที่มา : ปิยวดี เอ่งฉ้วน
ตัวอย่าง
จงหา ห.ร.ม. ของจำนวนที่กำหนด
- 54 และ 72
วิธีทำ
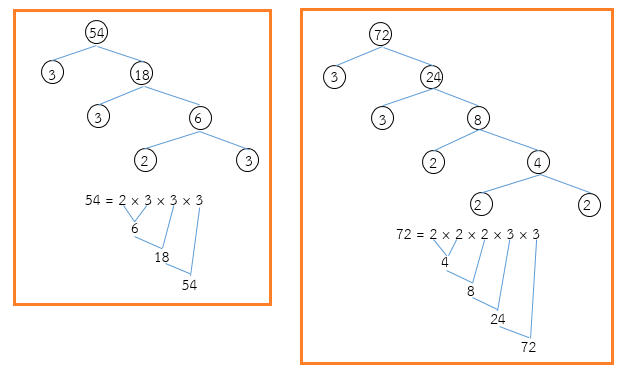
จากการแยกตัวประกอบของ 54 และ 72 เป็นจริง
ดังนั้น
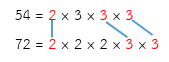
พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 54 และ 72 คือ 2, 3, 3
ดังนั้น ห.ร.ม. ของ 54 และ 72 คือ 2 × 3 × 3 = 18
ตอบ 18
ตรวจคำตอบ
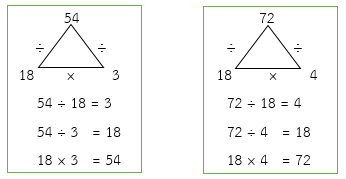
ห.ร.ม. ของ 54 และ 72 คือ 2 × 3 × 3 = 18
ดังนั้น เมื่อ 54 ÷ 18 = 3 และ 72 ÷ 18 = 4 แสดงว่า ห.ร.ม. คือ 18 เป็นจริง
- 72 และ 126
วิธีทำ
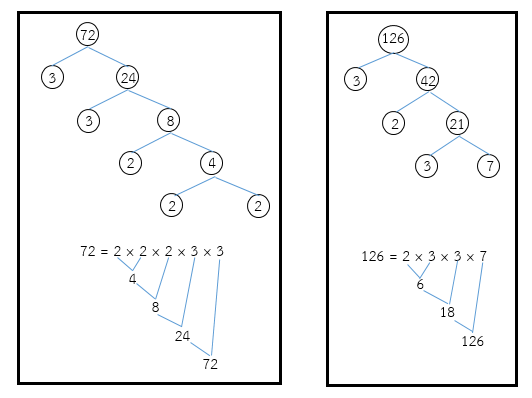

พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 72 และ 126 คือ 2, 3, 3
ดังนั้น ห.ร.ม. ของ 54 และ 72 คือ 2 × 3 × 3 = 18
ตอบ 18
ตรวจคำตอบ
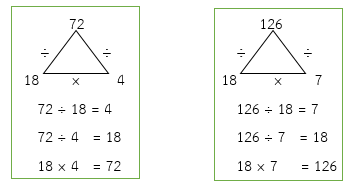
ห.ร.ม. ของ 72 และ 126 คือ 2 × 3 × 3 = 18
ดังนั้น เมื่อ 72 ÷ 18 = 4 และ 126 ÷ 18 = 7 แสดงว่า ห.ร.ม. คือ 18 เป็นจริง
- 16, 24 และ 40
วิธีทำ
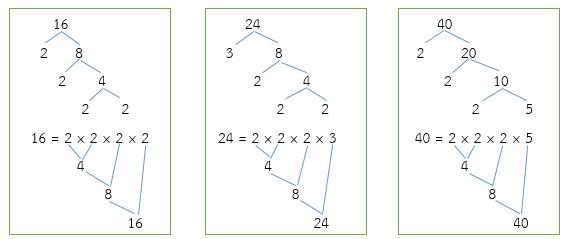
จากการแยกตัวประกอบของ 16, 24 และ 40 เป็นจริง
ดังนั้น
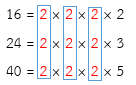
พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 16, 24 และ 40 คือ 2, 2, 2
ดังนั้น ห.ร.ม. ของ 16, 24 และ 40 คือ 2 × 2 × 2 = 8
ตอบ 8
ตรวจคำตอบ
ห.ร.ม. ของ 16, 24 และ 40 คือ 2 × 2 × 2 = 8
ดังนั้น เมื่อ 16 ÷ 8 = 2, 24 ÷ 8 = 3 และ 40 ÷ 8 = 5 แสดงว่า ห.ร.ม. คือ 8 เป็นจริง

- 84, 108 และ 120
วิธีทำ
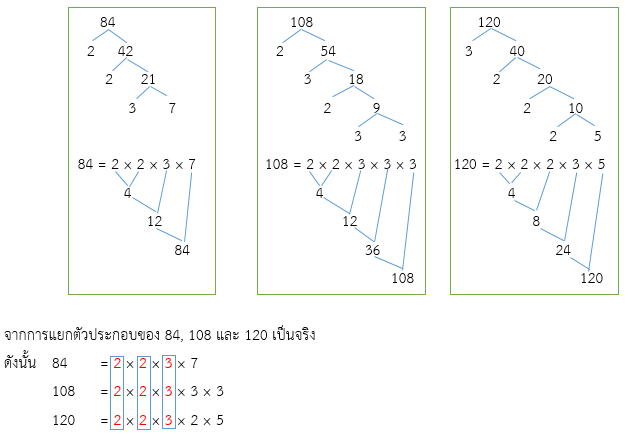
พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 84, 108 และ 120 คือ 2, 2, 3
ดังนั้น ห.ร.ม. ของ 84, 108 และ 120 คือ 2 × 2 × 3 = 12
ตอบ 12
ตรวจคำตอบ
ห.ร.ม. ของ 84, 108 และ 120 คือ 2 × 2 × 3 = 12
ดังนั้น เมื่อ 84 ÷ 12 = 7, 108 ÷ 12 = 9 และ 120 ÷ 12 = 10 แสดงว่า ห.ร.ม. คือ 12 เป็น
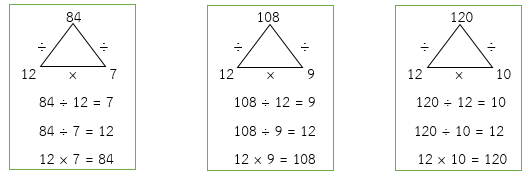
- 5. 132, 154 และ 198
วิธีทำ
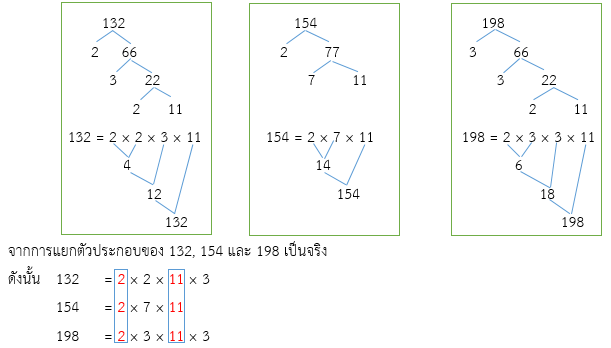
พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 132, 154 และ 198 คือ 2, 11
ดังนั้น ห.ร.ม. ของ 132, 154 และ 198 คือ 2 × 11 = 22
ตอบ 22
ตรวจคำตอบ
ห.ร.ม. ของ 132, 154 และ 198 คือ 2 × 11 = 22
ดังนั้น เมื่อ 132 ÷ 22 = 6, 154 ÷ 22 = 7 และ 198 ÷ 22 = 9 แสดงว่า ห.ร.ม. คือ 22 เป็นจริง
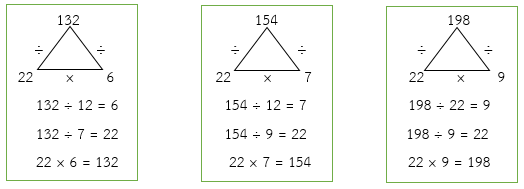
แหล่งที่มา
นิติกร ระดม. 2551. คู่มือครู อจท. คณิตศาสตร์ ป6. กรุงเทพมหานคร: อักษรเจริญทัศน์
กรมวิชาการ กระทรวงศึกษาธิการ. (2538). หนังสือเอกสารเสริมความรู้คณิตศาสตร์ ระดับประถมศึกษา อันดับที่3 (1). กรุงเทพมหานคร: โรงพิมพ์คุรุสภาลาดพร้าว.
ธิดาสิริ ภัทรากาญจน์. (2548). เกมคณิตปริศนา: พาสนุกปลูกปัญญา (3). กรุงเทพฯ: บริษัท ด่านสุทธาการพิมพ์ จำกัด
สำนักงานส่งเสริมการศึกษานอกระบบและการศึกษาตามอัธยาศัย. (2551). เอกสารสรุปเนื้อหาที่ต้องรู้รายวิชาคณิตศาสตร์ ระดับประถมศึกษา. กรุงเทพฯ:
สำนักงาน กศน.สำนักงานปลัดกระทรวงศึกษาธิการ.นางกนกวลี อุษณกรกุล. (2551). หนังสือเรียน รายวิชาพื้นฐาน คณิตศาสตร์ ม.1 เล่ม1 ชั้นมัธยมศึกษาปีที่ 1 (1). กรุงเทพมหานคร ; อักษรเจริญทัศน์
ทรงวิทย์ สุวรรณธาดา และคณะ. (2551). แบบฝึกหัด รายวิชาพื้นฐานกลุ่มสาระการเรียนรู้คณิตศาสตร์ คณิตศาสตร์ ป.6. กรุงเทพมหานคร: บริษัทแม็คเอ็ดยูเคชั่น จำกัด
กลับไปที่เนื้อหา
ตัวคูณร่วมของจำนวนนับตั้งแต่สองจำนวนขึ้นไปเป็นจำนวนนับที่จำนวนเหล่านั้นหารลงตัว
ตัวคูณร่วมน้อย (ค.ร.น.) ของจำนวนนับตั้งแต่สองจำนวนขึ้นไป หมายถึง จำนวนที่มีค่าน้อยที่สุด ซึ่งมีจำนวนนับนั้น ๆ ทุกจำนวน เป็นตัวประกอบ
การแยกตัวประกอบ เป็นการเขียนจำนวนนับในรูปการคูณของตัวประกอบเฉพาะ
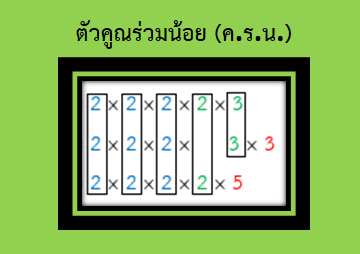
ภาพที่ 1 ตัวคูณร่วมน้อย (คูณร่วมน้อย)
ที่มา : ปิยวดี เอ่งฉ้วน
ตัวอย่าง
จงหา ค.ร.น. ของจำนวนที่กำหนด
- 12 และ 32
วิธีทำ
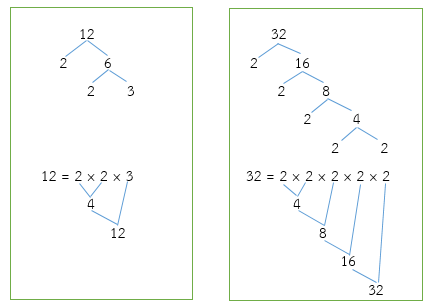
จากการแยกตัวประกอบของ 12 และ 32 เป็นจริง
ดังนั้น
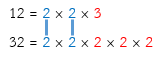
(1) พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 12 และ 32 คือ 2, 2
(2) ตัวประกอบเฉพาะที่เหลือของ 12 และ 32 คือ 3, 2, 2, 2
ดังนั้น ค.ร.น. ของ 12 และ 32 คือ 2 × 2 × 3 × 2 × 2 × 2 = 96
ตอบ 96
ตรวจคำตอบ
ค.ร.น. ของ 12 และ 32 คือ 96
เมื่อ

ดังนั้น 96 = (12 × 8), (32 × 3) เป็นจริง
- 2. 36 และ 45
วิธีทำ
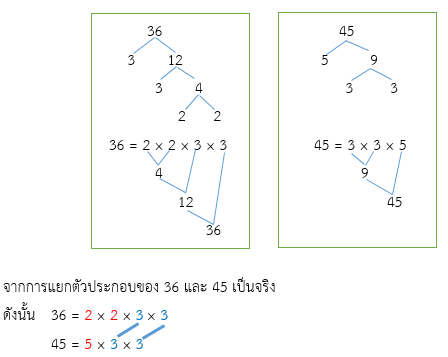
(1) พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 36 และ 45 คือ 3, 3
(2) ตัวประกอบเฉพาะที่เหลือของ 36 และ 45 คือ 2, 2, 5
ดังนั้น ค.ร.น. ของ 36 และ 45 คือ 3 × 3 × 2 × 2 × 5 = 180
ตอบ 180
ตรวจคำตอบ
ค.ร.น ของ 36 และ 45 คือ 180
เมื่อ

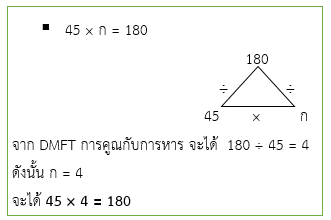
ดังนัน 180 = (36 × 5), (45 × 4) เป็นจริง
- 18, 27 และ 54
วิธีทำ
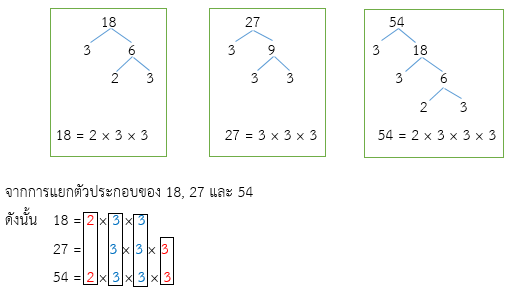
(1) พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 18, 27 และ 54 คือ 3, 3
(2) พิจารณาตัวประกอบเฉพาะที่เหลือที่เป็นตัวประกอบร่วมอย่างน้อยสองจำนวนของ 18, 27 และ 54
คือ 2, 3
ดังนั้น ค.ร.น. ของ 18, 27 และ 54 คือ 2 × 3 × 3 × 3 = 54
ตอบ 54
ตรวจคำตอบ
ค.ร.น. ของ 18, 27 และ 54 คือ 54
เมื่อ

ดังนั้น 54 = (18 × 3), (27 × 2) และ (54 × 1) เป็นจริง
- 48, 72 และ 80
วิธีทำ
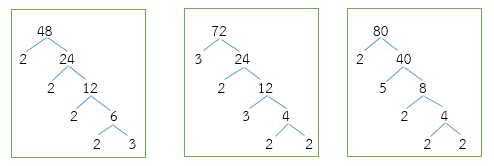
48 = 2 × 2 × 2 × 2 × 3
72 = 2 × 2 × 2 × 3 × 3
80 = 2 × 2 × 2 × 2 × 5
จากการแยกตัวประกอบของ 48, 72 และ 80
ดังนั้น
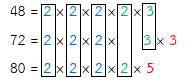
(1) พิจารณาตัวประกอบเฉพาะที่เป็นตัวประกอบร่วมทุกจำนวนของ 48, 72 และ 80 คือ 2, 2, 2,
(2) พิจารณาตัวประกอบเฉพาะที่เหลือที่เป็นตัวประกอบร่วมอย่างน้อยสองจำนวนของ คือ 2, 3
(3) ตัวประกอบเฉพาะที่เหลือของ 48, 72 และ 80 คือ 3, 5
ดังนั้น ค.ร.น. ของ 48, 72 และ 80 คือ 2 × 2 × 2 × 2 × 3 × 3 × 5 = 720
ตอบ 720
ตรวจคำตอบ
ค.ร.น. ของ 48, 72 และ 80 คือ 720
เมื่อ

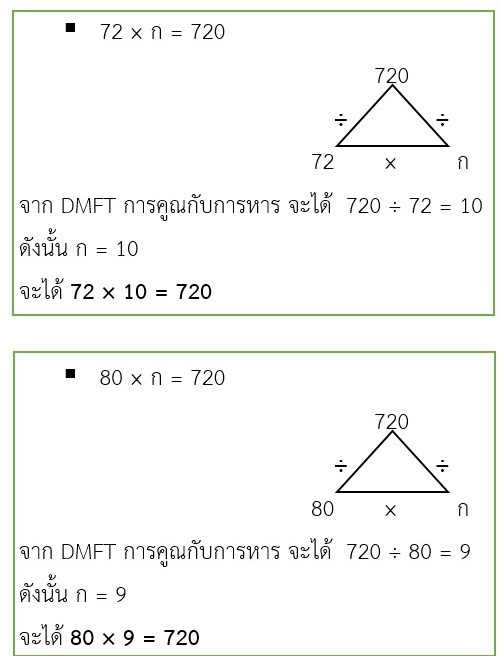
จาก DMFT การคูณกับการหาร จะได้ 720 ÷ 80 = 9
ดังนั้น ก = 9
จะได้ 80 × 9 = 720
ดังนั้น 720 = (48 × 15), (72 × 10) และ (80 × 9) เป็นจริง
แหล่งที่มา
นิติกร ระดม. 2551. คู่มือครู อจท. คณิตศาสตร์ ป6. กรุงเทพมหานคร: อักษรเจริญทัศน์
กรมวิชาการ กระทรวงศึกษาธิการ. (2538). หนังสือเอกสารเสริมความรู้คณิตศาสตร์ ระดับประถมศึกษา อันดับที่3 (1). กรุงเทพมหานคร: โรงพิมพ์คุรุสภาลาดพร้าว.
ธิดาสิริ ภัทรากาญจน์. (2548). เกมคณิตปริศนา: พาสนุกปลูกปัญญา (3). กรุงเทพฯ: บริษัท ด่านสุทธาการพิมพ์ จำกัด
สำนักงานส่งเสริมการศึกษานอกระบบและการศึกษาตามอัธยาศัย. (2551). เอกสารสรุปเนื้อหาที่ต้องรู้รายวิชาคณิตศาสตร์ ระดับประถมศึกษา. กรุงเทพฯ:
สำนักงาน กศน.สำนักงานปลัดกระทรวงศึกษาธิการ.นางกนกวลี อุษณกรกุล. (2551). หนังสือเรียน รายวิชาพื้นฐาน คณิตศาสตร์ ม.1 เล่ม1 ชั้นมัธยมศึกษาปีที่ 1 (1). กรุงเทพมหานคร ; อักษรเจริญทัศน์
ทรงวิทย์ สุวรรณธาดา และคณะ. (2551). แบบฝึกหัด รายวิชาพื้นฐานกลุ่มสาระการเรียนรู้คณิตศาสตร์ คณิตศาสตร์ ป.6. กรุงเทพมหานคร: บริษัทแม็คเอ็ดยูเคชั่น จำกัด
กลับไปที่เนื้อหา



